-
Paper Information
- Next Paper
- Previous Paper
- Paper Submission
-
Journal Information
- About This Journal
- Editorial Board
- Current Issue
- Archive
- Author Guidelines
- Contact Us
International Journal of Mechanics and Applications
p-ISSN: 2165-9281 e-ISSN: 2165-9303
2012; 2(6): 129-139
doi: 10.5923/j.mechanics.20120206.05
Fluid-Structure Interaction in a Stirred Vessel Equipped with a Rushton Turbine
S. Karray , Z. Driss , A. Kaffel , H. Kchaou , M. S. Abid
National Engineering School of Sfax (ENIS), Laboratory of Electro-Mechanic Systems (LASEM), University of Sfax, B.P. 1173, km 3.5 Road Soukra, 3038, Sfax, Tunisia
Correspondence to: Z. Driss , National Engineering School of Sfax (ENIS), Laboratory of Electro-Mechanic Systems (LASEM), University of Sfax, B.P. 1173, km 3.5 Road Soukra, 3038, Sfax, Tunisia.
| Email: |  |
Copyright © 2012 Scientific & Academic Publishing. All Rights Reserved.
In this paper, a problem of fluid-structure interaction in a mixing vessel equipped with a Rushton turbine is solved with partitioned coupled fluid-structure interaction computational analysis. The computational fluid dynamics (CFD) code, based on the finite volume method, is used for determination of the flow field in the mixing vessel. The results in form of pressure distribution are then applied to the blade model, which is then analyzed with the computational structure dynamics (CSD) code, based on the finite element method. The resulting displacement is evaluated. The proposed procedure can be effectively used for optimization of structures with significant fluid flow influences. The comparison of the velocity profile with the results founded in the literature shows a good comparison. This proves the validity of the numerical method.
Keywords: Computational Fluid Dynamics (CFD), Computational Structure Dynamics (CSD), Fluid-Structure Interaction (FSI), Coupling Algorithm, Rushton Turbine, Turbulent Flow
Cite this paper: S. Karray , Z. Driss , A. Kaffel , H. Kchaou , M. S. Abid , "Fluid-Structure Interaction in a Stirred Vessel Equipped with a Rushton Turbine", International Journal of Mechanics and Applications, Vol. 2 No. 6, 2012, pp. 129-139. doi: 10.5923/j.mechanics.20120206.05.
Article Outline
1. Introduction
- The mutual interaction between a fluid flow and a deforming structure is referred to fluid–structure interaction (FSI). Life saving examples are the opening of a parachute[1] or an air bag[2]. Undesired occurrences of fluid–structure interaction are collapses of bridges[3] and cooling towers due to wind and also flutter of aircraft wings[4] and turbine blades[5]. In the biomedical field, the interaction between an elastic artery[6,7] or a heart chamber[8] and the blood that flows through them is of interest. Also for the design of artificial heart valves[9,10], fluid–structure interaction needs to be taken into account. Though efficient solvers for both the fluid and the structural dynamics exist, the development of tools for modeling various FSI problems remains a challenge. As was already mentioned and in order to describe these problems, an exchange of data has to take place between the fluid and structural fields. Based on this data exchange, the methods for solving fluid-structure interaction problems can be divided into monolithic[11-13], and partitioned couplings[14-16]. The first consists on solving both parts of fluid and structure in the same system of equations. The choice of time step is only limited by the required precision. However, this type of algorithm requires a development of a computer code. Moreover, the numerical methods employed for the fluid and the structure domains are different and are difficult to place within the same code,hence the utility of the partitioned algorithm methodology. In the partitioned method, the fluid and structural parts are solved separately. The main advantage of this method is that it allows already developing efficient and well validated solvers for both the fluid and structure subtasks to be combined. Some theoretical and numerical studies of partitioned coupling algorithms for one and two dimensional problems can be found[17]. Particularly, commercial codes for combining existing solvers have been developed. This method has been introduced by Park and Felippa[18], and further investigated by Wood[19]. Various experimental and numerical simulations study the fluid behavior, when the movement of the structure is prescribed analytically[20-22]. Other researchers concentrated on the fluid part, while a simple structural model for a rigid body was used[13]. Further simplifications have been done by neglecting the dynamic effects and simulating static FSI. For example, Beckert et al.[24] used a multivariate interpolation scheme for coupling fluid and structural models in three dimensional spaces. They applied it to static aeroelastic problems, in order to predict the equilibrium of elastic wing models in transonic fluid flow. Seiber[25] developed an efficient coupling algorithm combining FASTEST-3D code and FEAP code for solving various fluid-structure interaction problems in three-dimensional domains for arbitrary elastic structures. Glück et al.[26] applied a partitioned coupling between the CFD code FASTEST-3D and the CSD code ASE to thin shells and membranous structures with large displacements. Bucchig nani et al.[27] presented a numerical code to study the problem of an incompressible flow in a stirred vessel. It was based on a method of a partition treatment type, with the fluid and structural fields resolved by coupling two distinct models. Wang[28] provided an effective new idea to solve aeroelasticity problems, in which the tools Fluent and ABAQUS/ANSYS are employed. Ghavanloo et al.[29] present a simple analytical approach for stationary interaction between the fluid and the cylindrical membrane. They explain the effect of the equilibrium membrane forms elasticity on fluid system. Dang et al.[30] used a coupling algorithm to study the stationary behaviour of a flexible aircraft wing. The finite element method is used for the discretization of the two areas of the structure and fluid.In this paper, a computational analysis of the fluid-structure interaction in a mixing vessel is presented. In mixing vessels, the fluid can have a significant influence on the deformation blades of during mixing, depending on turbine speed and fluid viscosity. For this purpose, a coupling algorithm has been performed to determine the fluid influences on the Rushton turbine. The fluid field in the mixing vessel was first analyzed with the computational fluid dynamics (CFD) code. The results in the form of pressure were then applied to the blade model, which was the analyzed with the computational structure dynamics (CSD) code. The content of this paper is organized as follows: Section 2 describes the geometry of the system. Section 3 describes the coupling algorithm. Section 4 presents the numerical results. Section 5 contains concluding remarks.
2. Stirred Vessels Configuration
- The system was made of a flat bottom cylindrical vessel of diameter D=293 mm, and the liquid height in the vessel was H=D. A Rushton turbine of thickness e=1 mm was attached on the inside wall of the cylindrical tank. It has two arms of diameter d=0.33 D (Figure 1).
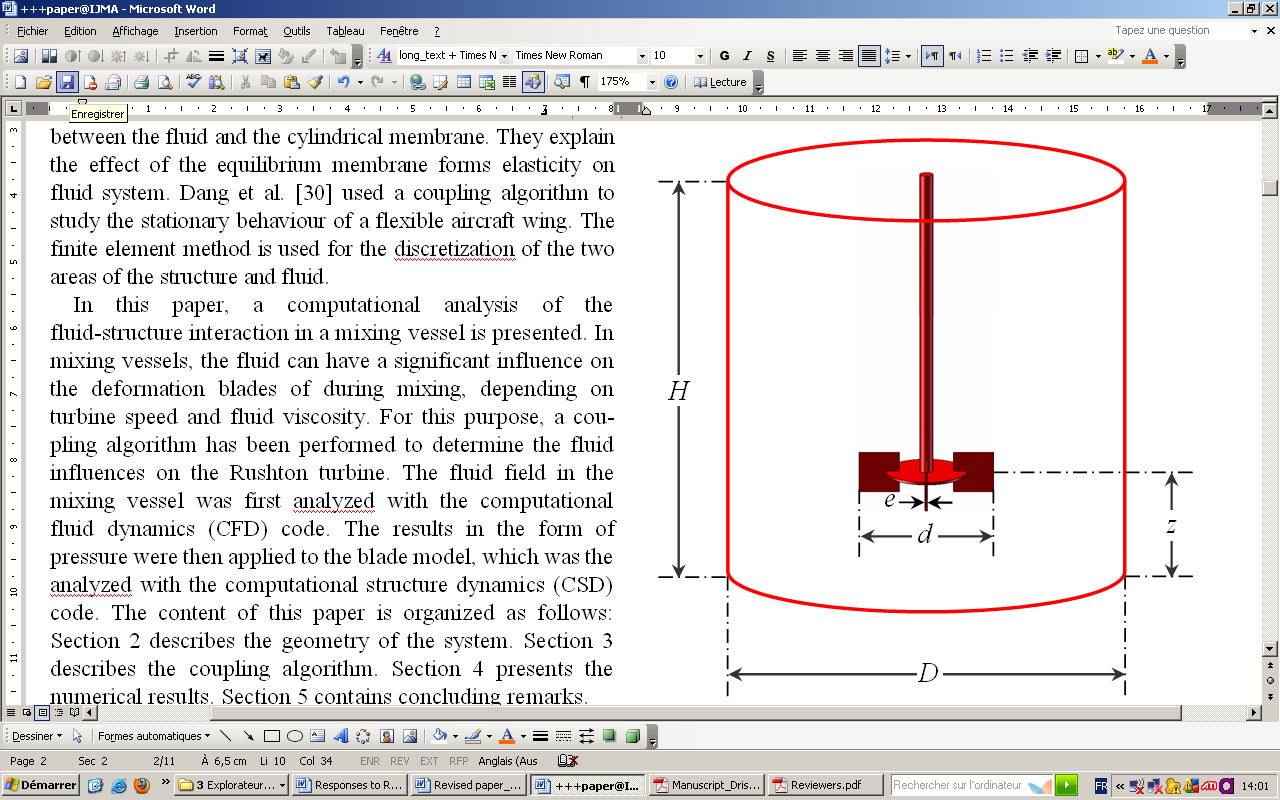 | Figure 1. Stirred vessel equipped with Rushton turbine |
3. Coupling Algorithm
- In order to make a computational simulation for the fluid-structure interaction phenomena, we used a coupling algorithm to deal with problems of strongly non-linear FSI[32-33]. This algorithm is based on a partitioned method. This method determines the structural and flow solution vectors independently from each other, updating afterwards the relevant boundary conditions. This algorithm requires a CSD code, a CFD code and a coupling interface.
3.1. CFD code
- The CFD code allows the hydrodynamic calculation of the fluid[34-37]. The finite volumes method is adopted for the treatment of these equations. Initially, the fluid field is being divided into elementary volumes representing the geometry of the problem. Secondly, the differential equations are discretized using the control volume approach[38]. Several quantities can be found such as the velocity field, pressure, turbulent kinetic energy and its dissipation rate. In a fluid flow problem, we need to know the pressure value at the level of the fluid structure interface. Also, this code must be able to receive information representing displacement of the structure part to be used to solve the fluid flow problem.
3.2. CSD code
- The CSD code allows the static calculation of the structure. More precisely, this code must be able to receive information representing the varying physical forces in time exerted by the fluid on the fluid-structure interface. On the other hand, this code is used to determine the displacement of the nodes.
3.3. Coupling Interface
- The coupling interface ensures the transfer of the forces and displacements mentioned above, when the mesh in each fluid and structure codes is different. It organizes the transfer of information in time and makes an effective coupling between the fluid and structure codes. For every iteration, the force exerted by the fluid is calculated in the CFD code. The geometry is updated at the interface to calculate the structural displacement by the CSD code. Therefore, the role of the coupling algorithm is to exchange nearly any kind of data between the coupled codes. The iteration steps are stopped when the convergence is reached. The coupling algorithm was used to study a Rushton turbine in a vessel tank.
4. Numerical Results
4.1. CFD Results
- Following the implementation of the CFD code developed in our laboratory LASEM[39], we present the hydrodynamic results such as the velocity field and the turbulence characteristics.
4.1.1. Flow Patterns
- Figure 2 shows a velocity vector plot (U,V) in the r-θ plane for six iterations of the coupling algorithm defined by the axial position equal to z=0.66. These results confirm that the velocity field is very high in magnitude on the level of the field swept by the turbine blades. Also, it’s noted a predominance of a tangential flow due to the setting in rotation of the volume of the fluid located between blades. Far from the turbine, it’s noted a progressive deceleration of the flow. Moreover, the turbine undergoes a deformation due to the flexion of the blade. For thus, the velocity field changes slightly from iteration to another. In fact, after certain iterations (ni > 4), the turbine becomes deformed, and the velocity field is preserved (Figure 2.d).Figure 3 shows the secondary flow (U,W) in the r-z plane defined by the angular coordinates equal to θ=45°. This presentation plane thought the right blade in an initial state undeformed. The velocity fields show the presence of a radial jet on the level of the turbine. This jet changes against the walls of the tank with two axial flows thus forming two recirculation zones on both sides of the turbine. In addition, we observe that the axial jet is more intense during the first iteration. From iteration to another, the axial jet weakens. This fact generates an increase of the dead zone in the tank top. Indeed, the position of the circulation zone approaches towards the turbine axis. This phenomenon is completely logical since the position of the various planes representation during the iterations was deviated compared to the blade of the turbine which behaves like a curved blade turbine after deformation. By comparing the various iterations between them, it’s noted a weak variation of the velocity field starting from the second iteration.
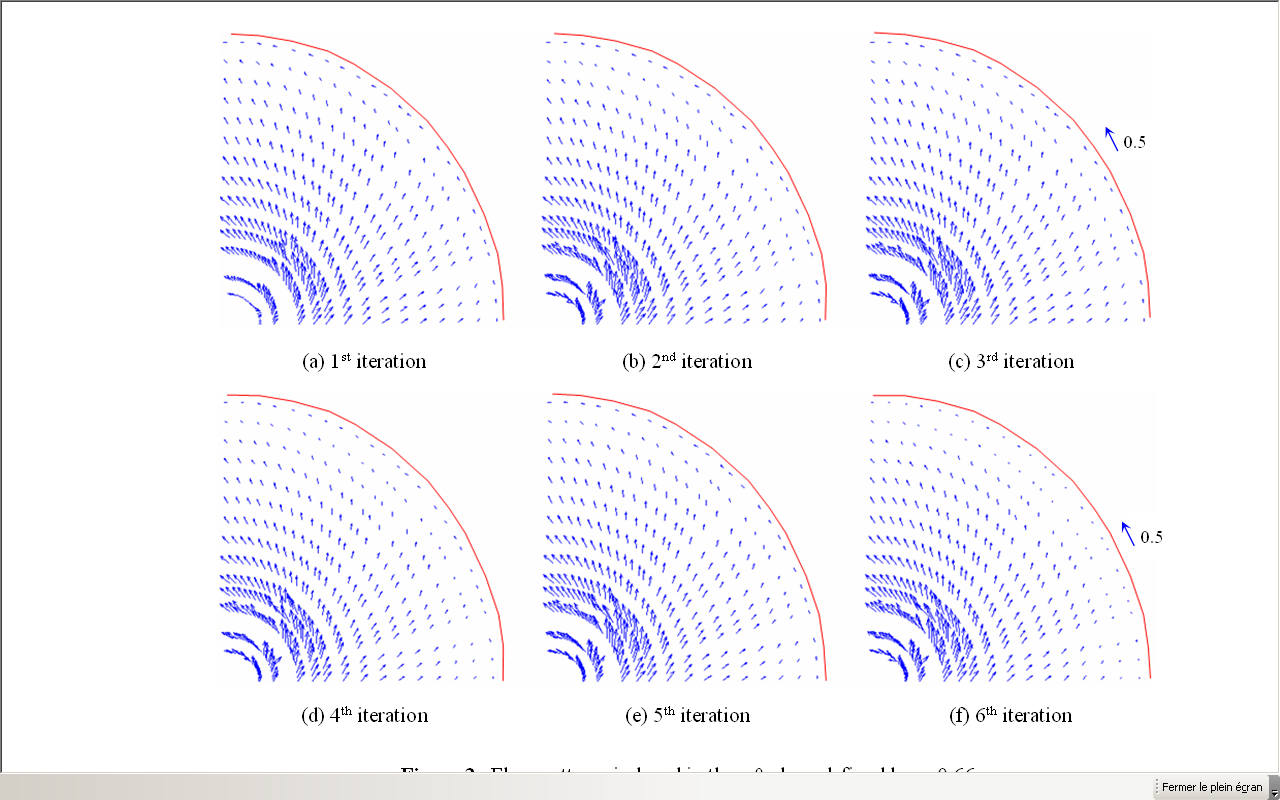 | Figure 2. Flow patterns induced in the r-θ plane defined by z=0.66 |
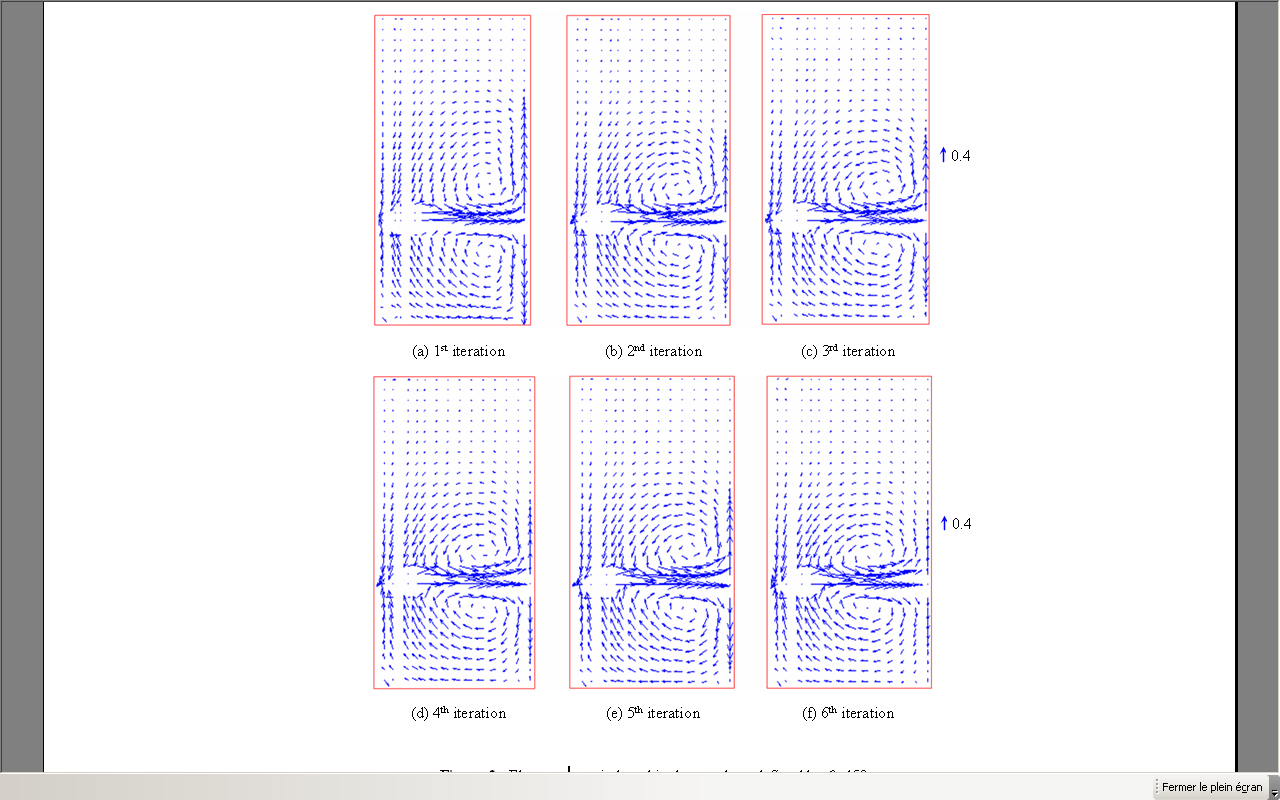 | Figure 3. Flow patterns induced in the r-z plane defined by θ=45° |
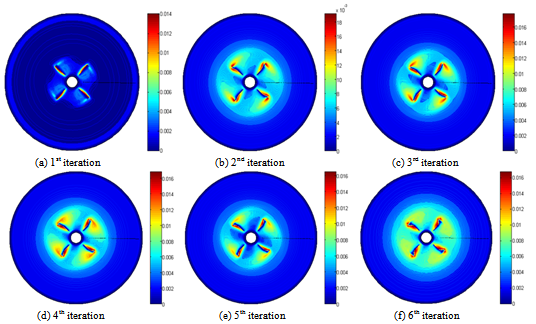 | Figure 4. Distribution of the turbulent kinetic energy in r-θ plane |
4.1.2. Distribution of the Turbulent Kinetic Energy
- Figure 4 presents the evolution of the distribution of the turbulent kinetic energy k in the horizontal plane defined by the axial position equal to z=0.66. Figure 5 presents the distribution of the turbulent kinetic energy k in the r-z plane during the six iterations of the coupling algorithm. This plane is located at the level of the turbine blade and defined by the angular position equal to θ=45°. According to these results, it’s noted that the maximum values are located in the wake developed upstream of the turbine blade. In the field swept by the turbine blade, the turbulent kinetic energy remains rather high. Outside this domain, the turbulent kinetic energy quickly becomes very low. By comparing these results from iteration to another, we observe that the maximal values are reached during the second iteration and it’s equal to k=0.018.4.1.3. Distribution of Dissipation Rate of the Turbulent Kinetic EnergyFigure 6 shows the distribution of the dissipation rate of the turbulent kinetic energy ε in the horizontal plane during the six iterations of the coupling algorithm. This plane correspond to an axial position defined by z=0.66. Figure 7 shows the distribution of the dissipation rate of the turbulent kinetic energy ε in the r-z plane for an angular position equal to θ=45° during the first six iterations of the algorithm of coupling. Globally, we observe a distribution similar to that already obtained with the turbulent kinetic energy. Indeed, it’s noted that the maximal values are located near the blade end. However, the rate of wake becomes very weak outside the domain swept by the turbine blades. The maximal value of the dissipation rate of the turbulent kinetic energy is reached in the sixth iteration and it is equal to ε=0.032.
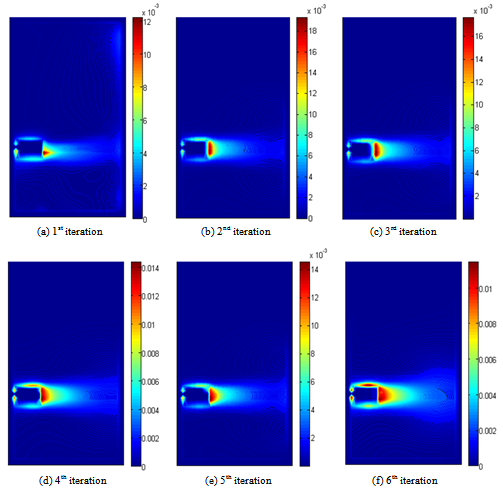 | Figure 5. Distribution of the turbulent kinetic energy in r-z plane |
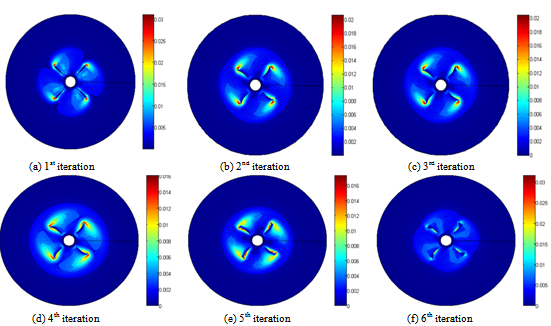 | Figure 6. Dissipation rate of the turbulent kinetic energy ε in the r-θ plane defined by z=1 |
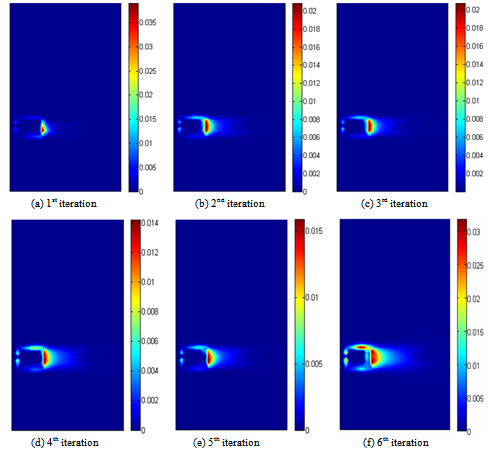 | Figure 7. Dissipation rate of the turbulent kinetic energy ε in the r-z plane defined by θ=45° |
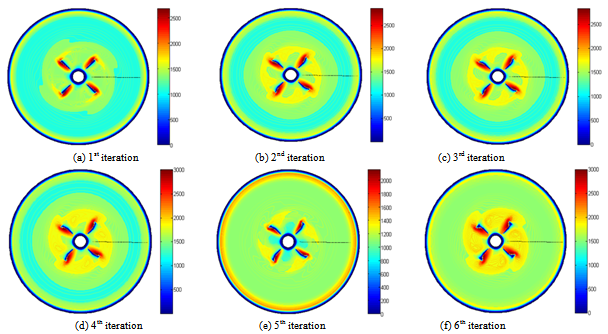 | Figure 8. Turbulent viscosity in the r-θ plane defined by z=0.16 |
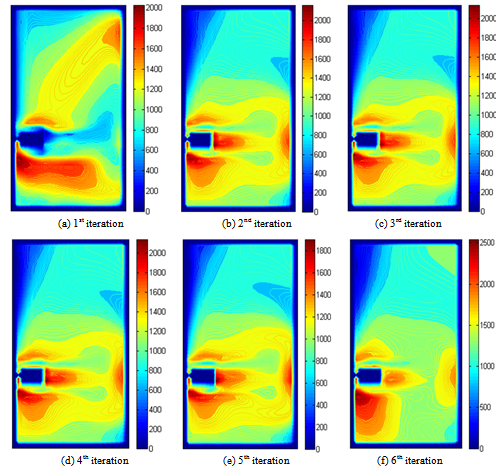 | Figure 9. Turbulent viscosity in the r-z plane defined by θ=45° |
4.1.4. Distribution of the Turbulent Viscosity
- Figure 8 shows the evolution of the distribution of the turbulent viscosity in the horizontal plane located in the bottom of the turbine during the iterations of the coupling algorithm. The presentation plane corresponds to the axial position equal to z=0.66. Figure 9 presents the distribution of the turbulent viscosity in the vertical plane defined by the angular position equal to θ=45°. It corresponds to the plane located at the level of the turbine blade. In these conditions, the vertical arm deformation reaches the representation plane. This is visualized by the presence of a zone where the turbulent viscosity of the fluid is null. This zone corresponds to the blade of the Rushton turbine in the initial state (Figure 9.a). Then, it decreases from iteration to another. Also, we find that the maximum value of the turbulent viscosity is obtained during the sixth iteration and is equal to υt=2500 (Figure 9.c). Indeed, it’s noted that the turbulent viscosity remains rather high in the field swept by the turbine blade. However, the turbulent viscosity quickly decreases near the walls. This phenomenon is due to the slowing down of the flow.
4.1.5. Comparison with Anterior Results
- Figure 10 presents the radial profiles of the dimensionless angular velocity component V(r). The axial coordinate is equal to z=0.7. In this figure, the results found by Alcamo et al.[40] are superposed. The error is equal to 9%. The good agreement between the results confirms the validity of the numerical method.
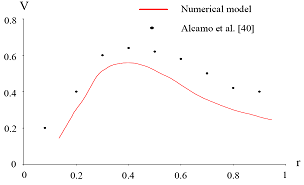 | Figure 10. Radial profiles of the angular velocity V(r) |
4.2. Static Studies
- In the static studies, we are interested in the structural part of the mixing system. Particularly, the static behavior of the Rushton turbine and the deformation of the blade under the flow effect have been studied. The discretisation is ensured by finite elements method. In these conditions, 2411 tetrahedral type nodes defined on the axis and the disc of the turbine. However, 245 quadratic type nodes arevdefined on etch blade (Figure 11). Figure 12 presents the results from the CSD code to study the static behaviour of the Rushton turbine and the evolution of the displacement field of the blade during various iterations of our coupling algorithm. Particularly, we are interested in the nodal displacement of the turbine blade to mesh the fluid domain. This operation is repeated several times until equilibrium is obtained. According to these results, it’s noted that the maximal displacement is obtained in the first iteration.
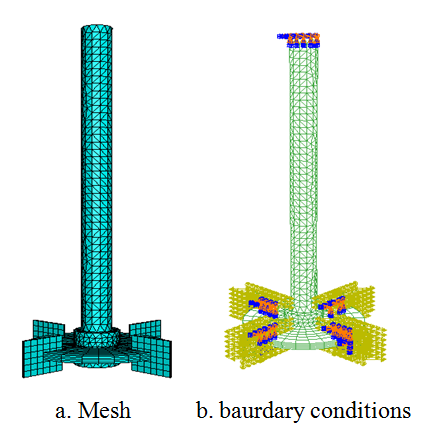 | Figure 11. Meshing |
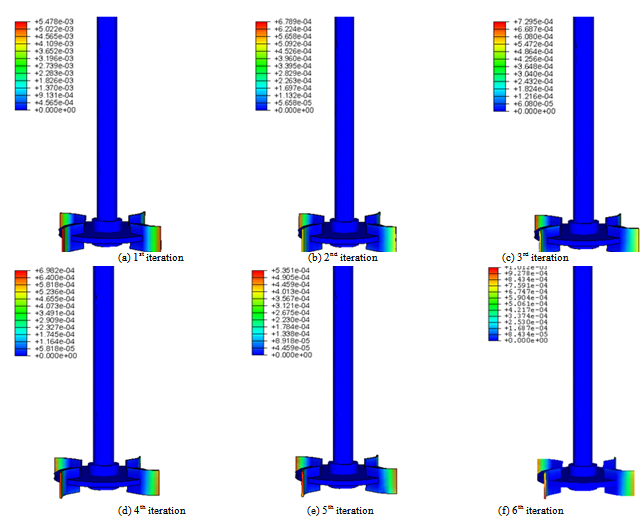 | Figure 12. Displacement field of the turbine Rushton |
5. Conclusions
- In this paper, coupling codes are used for solving fluid-structure interaction (FSI) problems in the stirred tank equipped by a Rushton turbine. A computational fluid dynamics (CFD) code and a computational structural dynamics (CSD) code have been coupled by using an efficient coupling interface. Particularly, the fluid field in stirred tank was solved by the CFD code in turbulent regime. The deformation of the Rushton turbine was solved by the CSD code. Specific techniques of rearrangement of grid and treatment of the boundary conditions are used to follow the behaviour of the system. This method takes advantage of the parallel process involved with each analysis code. This allows both parts of the fluid-structure interaction problem to be solved in the best possible way: a Finite Volume Method for the fluid dynamics and a Finite Element Method for the structure. The CFD results obtained allow a visualizing of the velocity field, the turbulent kinetic energy, the dissipation rate of the turbulent kinetic energy, the turbulent viscosity and the mechanical deformation. These results proof that the fluid flow have a significant effect on the deformation of the Rushton turbine blade. For thus, it’s fundamental to take consideration of this phenomenon in the design of the industrial process.
NOMENCLATURE
- d turbine diameter, mz Height of the blade, me Thickness of the blade, mD Internal diameter of the vessel tank, m Fr Froude number, dimenionlessz turbine position, mH vessel tank height, mk turbulent kinetic energy, dimensionlessRe Reynolds number, dimensionless, r radial coordinate, dimensionlesss shaft diameter, m U radial velocity components, dimensionlessV angular velocity components, dimensionlessW axial velocity components, dimensionlessz axial coordinate, dimensionlessni iteration numberυt turbulent viscosity
 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-Text HTML
Full-Text HTML