A. Kleshchev
St. Petersburg State Marine Technical University, st. Lotsmanskaya 3, St. Petersburg, 190008, Russia
Correspondence to: A. Kleshchev , St. Petersburg State Marine Technical University, st. Lotsmanskaya 3, St. Petersburg, 190008, Russia.
| Email: |  |
Copyright © 2012 Scientific & Academic Publishing. All Rights Reserved.
Abstract
The real scatterers have non – analytical form and therefore the method of the division of the variables does not approach by the calculation of the reflection from their. In the article is presented the method of the integral equations Fredholm of the first and second kinds for the solution of the problem of the sound diffraction on the ideal non – analytical scatterers. In detail is giving the analysis of the improper integrals and are calculating the moduluses of the moduluses of the scattered pressure for the non – analytical bodies.
Keywords:
Diffraction, Integral Equation, Non – analytical Form, Boundary Conditions
Cite this paper:
A. Kleshchev , "Method of Integral Equations in Problem of Sound Diffraction on Bodies of Non – analytical Form", International Journal of Mechanics and Applications, Vol. 2 No. 6, 2012, pp. 124-128. doi: 10.5923/j.mechanics.20120206.04.
1. Introduction
The method of the integral equations is using in problems of the sound diffraction on the ideal and elastic bodies non – analytical form for the calculation of the angular characteristics of the sound scattering on the equal footing with the different: the method of the boundary elements and the method of the T – matrixes.The main target of the given research is appearing the determination of the angular distributions of the scattered pressure, that is important for the practical hydrolocation.
2. The Ideal Scatterer of the Non – analytical Form
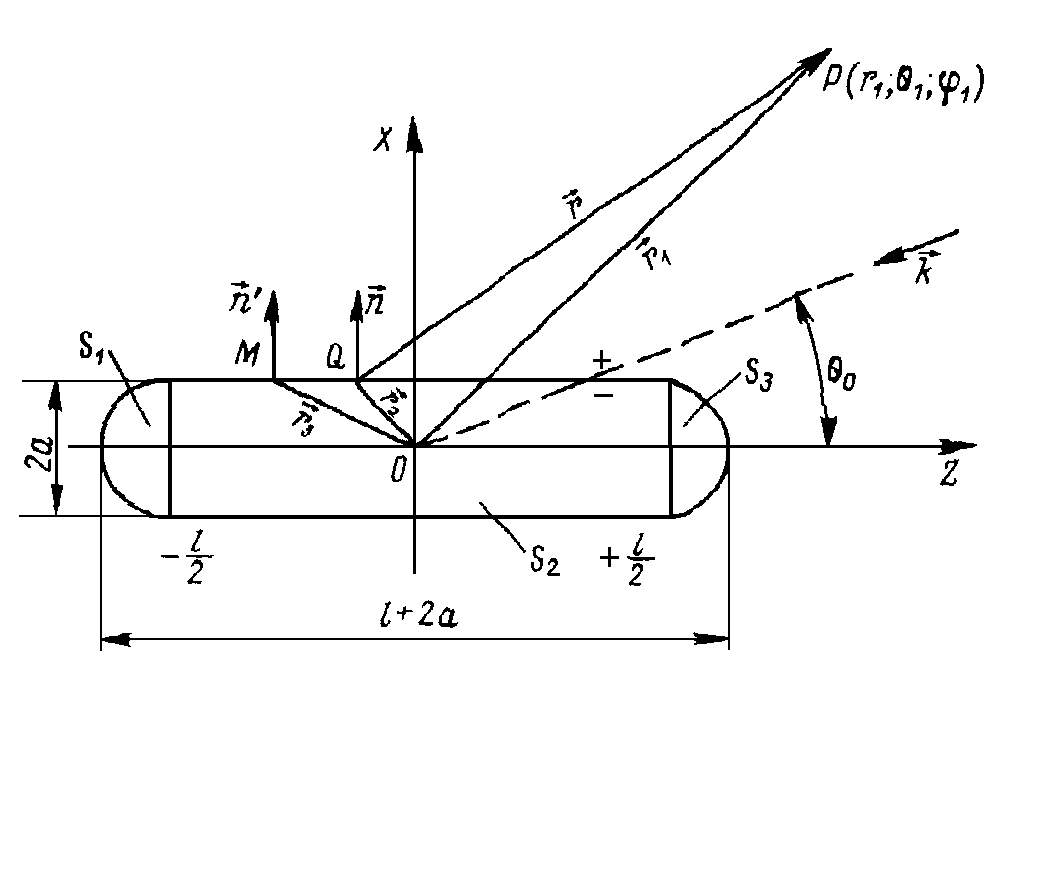 | Figure 1. The non – analytical smooth scatterer in the form of the cylinder with the semi – spheres |
We discern the ideal non – analytical scatterer in the form of the terminal cylinder with the semi – spheres on its ends (see fig. 1).The pressure 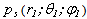 in the scattered wave in the point observation
in the scattered wave in the point observation 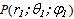 is equally[ 1, 2 ]:
is equally[ 1, 2 ]: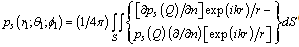 | (1) |
where Q – the point of the surface of the scatterer.For the ideal soft scatterer ( the homogeneous Dirichlet condition) the scattered pressure is equally: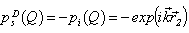 for the ideal hard scatterer ( the homogeneous Neimann’s condition):
for the ideal hard scatterer ( the homogeneous Neimann’s condition):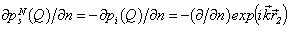 Then (1) for the Dirichlet condition at the surface is accepting the appearance:
Then (1) for the Dirichlet condition at the surface is accepting the appearance: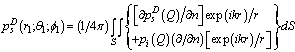 | (2) |
for the Neimann’s condition: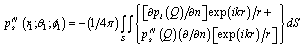 | (3) |
We are combining the point of the observation P 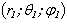 with the point of the surface scatterer
with the point of the surface scatterer 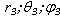 . Тhen (2) is transform in the Fredholm equation of the first kind for the function
. Тhen (2) is transform in the Fredholm equation of the first kind for the function 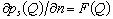 ( with the account of the Dirichlet condition):
( with the account of the Dirichlet condition):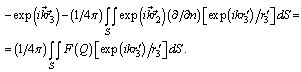 | (4) |
We are differentiate the left and right parts of the equation (3) with 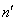 and are use the boundary Neimann’s condition, then we are get integro – differential equation for the funktion
and are use the boundary Neimann’s condition, then we are get integro – differential equation for the funktion 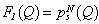 :
: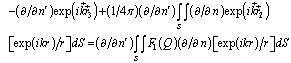 | (5) |
This problem can solve with the help of the Fredholm equation of the second kind. For the Dirichlet condition we are get the equation for the function 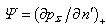 , where the sign «+» is mean the outside domain to S . For the Dirichlet condition th pressure pΣ is continuous by the crossing through the boundary S:
, where the sign «+» is mean the outside domain to S . For the Dirichlet condition th pressure pΣ is continuous by the crossing through the boundary S: 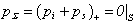 and
and 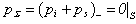 , while the function
, while the function 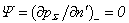 (since inside – the vacuum) , but outside -
(since inside – the vacuum) , but outside - 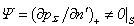 .The function
.The function 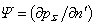 we are find from the solution of the non – homogeneous Fredholm equation of the second kind[ 1, 2 ]:
we are find from the solution of the non – homogeneous Fredholm equation of the second kind[ 1, 2 ]: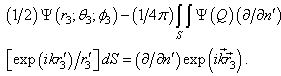 | (6) |
The integral to the left of (6) must understand in the sense of the main meaning.With the help Ψ we are find and the scattered pressure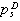 in the any point of the medium
in the any point of the medium 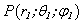 :
: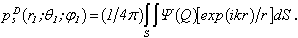 | (7) |
For the Neimann’s condition we are bring the function 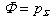 - the solution of the Fredholm equation of the second kind[ 1, 2 ]:
- the solution of the Fredholm equation of the second kind[ 1, 2 ]: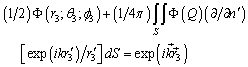 The scattered pressure in the point
The scattered pressure in the point 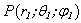 we are express through the function Ф:
we are express through the function Ф: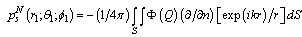 | (8) |
The scattered pressure 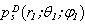 can find either with the help of the integral (2) (for the Fredholm equation of the first kind), or with the help of the equation (7) (for the Fredholm equation of the second kind).The surface S is consist of S2 and of the surfaces S1 и S3 (see fig. 1).For the calculation of the integrals (2) and (7) on surface
can find either with the help of the integral (2) (for the Fredholm equation of the first kind), or with the help of the equation (7) (for the Fredholm equation of the second kind).The surface S is consist of S2 and of the surfaces S1 и S3 (see fig. 1).For the calculation of the integrals (2) and (7) on surface 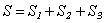 we are choose the grid of the nodal points. We are mark the nodal point through
we are choose the grid of the nodal points. We are mark the nodal point through 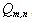 , where the index m is point out the room on the element, while the index n – on guide. The integrals (2) and (7) we are substitute the numerical quadratures
, where the index m is point out the room on the element, while the index n – on guide. The integrals (2) and (7) we are substitute the numerical quadratures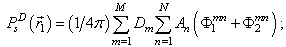 | (9) |
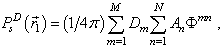 | (10) |
where 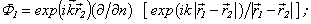
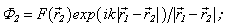
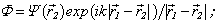
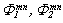 and
and 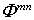 - the values of the functions Ф1, Ф2, and Ф in the nodal points Qmn; An, Dm – the weight coefficients; М – the quantity of the nodal points on the element, N – the quantity of the nodal points on the guide.The unknown functions
- the values of the functions Ф1, Ф2, and Ф in the nodal points Qmn; An, Dm – the weight coefficients; М – the quantity of the nodal points on the element, N – the quantity of the nodal points on the guide.The unknown functions 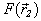 and
and 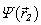 we are find from the solution of the Fredholm equation of the first kind (4) and of the Fredholm equation of the second kind (6).Transformed in (4) to the numerical quadratures, we are get the algebraice system of the equations of the order
we are find from the solution of the Fredholm equation of the first kind (4) and of the Fredholm equation of the second kind (6).Transformed in (4) to the numerical quadratures, we are get the algebraice system of the equations of the order 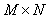 relatively Fmn – of the meanings
relatively Fmn – of the meanings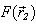 in nodal points:
in nodal points: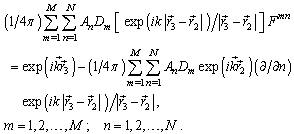 | (11) |
If we are taking advantage of the symmetry of the problem relatively 0f the plane XOZ, that from the system 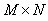 of the equations we transform to the system MN/2 (N – the even number), but by
of the equations we transform to the system MN/2 (N – the even number), but by 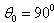 - to the system MN/4 (M and N - the even numbers). Easily see from fig. 1, that by
- to the system MN/4 (M and N - the even numbers). Easily see from fig. 1, that by 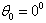 means of the function
means of the function 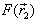 dependn’t on the angle
dependn’t on the angle 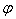 , that is
, that is 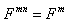 for everybody n = 1,2,…,N, and we get the system M – order. In correspondence with the integral of Kirchhoff the special point
for everybody n = 1,2,…,N, and we get the system M – order. In correspondence with the integral of Kirchhoff the special point 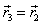 isolates in the equations (4). In the equation (6) the special point
isolates in the equations (4). In the equation (6) the special point 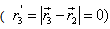 appearsn’t isolated, therefore the integral in the left part of the equation is considering in the meaning of the main value. For the calculation of this integral was using the following method. In the expression under the integral sign is appropriating the term of the simple analytical form, containing the singularity, which is integrating analytically. The staying part of the integral has the isolated special point and the corresponding integral is calculating by the help of the numerical method. The integral is showing in the kind of the three integrals:
appearsn’t isolated, therefore the integral in the left part of the equation is considering in the meaning of the main value. For the calculation of this integral was using the following method. In the expression under the integral sign is appropriating the term of the simple analytical form, containing the singularity, which is integrating analytically. The staying part of the integral has the isolated special point and the corresponding integral is calculating by the help of the numerical method. The integral is showing in the kind of the three integrals: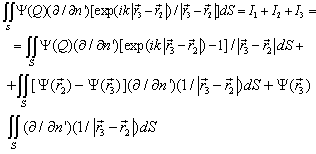 | (12) |
The integral 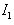 has not of the special point by
has not of the special point by 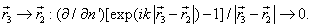 The integral
The integral 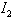 has the special point of the lesser kind and also is integrating by the numerical method.We cross to the calculation of the integral
has the special point of the lesser kind and also is integrating by the numerical method.We cross to the calculation of the integral 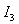 and consider firstly the integral:
and consider firstly the integral: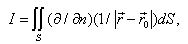 | (13) |
where 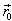 – the radius – vector of the point, which belongn’t to the surface S.From the Green’s formula is getting:
– the radius – vector of the point, which belongn’t to the surface S.From the Green’s formula is getting: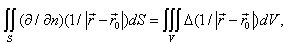 where V – the volume, limited on the surface S.We know, that:
where V – the volume, limited on the surface S.We know, that: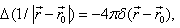 where
where 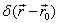 - delta function, satisfying to the relation:
- delta function, satisfying to the relation: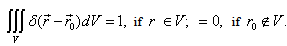 Therefore the integral I in (13) is equal:
Therefore the integral I in (13) is equal: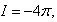 if the point is finding inside of the surface S and I=0, if is finding outside of the surface S. In the our version the point is finding on the surface S and the integral in the sense of the main meaning is equal:
if the point is finding inside of the surface S and I=0, if is finding outside of the surface S. In the our version the point is finding on the surface S and the integral in the sense of the main meaning is equal: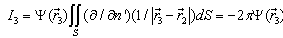 | (14) |
Substituted (14) and (12) in the integral Fredholm equation of the second kind (6), we get: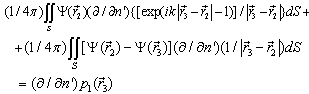 | (15) |
If we introduce the designation (fig. 1):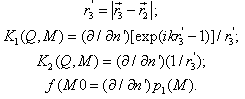 that the equation (15) has the form:
that the equation (15) has the form: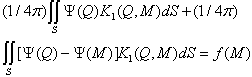 | (16) |
For the chosen soft scatterer in the form of the cylinder with the semi – spheres were found the values 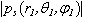 by the following parameters: a=1m, l=1m, ka=1, θ0 =
by the following parameters: a=1m, l=1m, ka=1, θ0 = 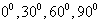 .At fig. 2-a and 2-b are present
.At fig. 2-a and 2-b are present 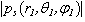 for the chosen parameters by θ0 =
for the chosen parameters by θ0 = 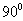 ( fig. 2-a) and θ0 =
( fig. 2-a) and θ0 = 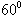 ( fig. 2-b) (the curve 1 corresponds to method of the T – matrixes, but the curve 2 – to the method of the integral equations).
( fig. 2-b) (the curve 1 corresponds to method of the T – matrixes, but the curve 2 – to the method of the integral equations).
3. The elastic Scatterer of the Non – analytical Form
The scattered field for the elastic bodies of the non – analytical form was determined either with the help of the method of the T – matrixes[3] or on the basis of the method of the boundary elements[4]. We are going to spread the method of the integral equations, used in[3] and[2] for the ideal non – analytical scatterers, on the elastic shell of the non – analytical form[5]. | Figure 2. 2-a. The modulus of the angular distribution of the scattered pressure. Fig. 2-b. The modulus of the angular distribution of the scattered pressure |
In the quality of the such scatterer we are going to consider the terminal isotropic elastic cylindrical shell with the semi – spheres on its ends (see fig. 3). The density of the material of the shell is ρ1, the Lame’s coefficients - λ and μ. The shell was filled in the internal liquid medium with the density ρ2 and the sound velocity C3 and it was placad in the external liquid medium with the density ρ0 and the sound velocity C0. At the shell falls the plane harmonic wave with pressure pi under the angle Θ0 and with the wave vector 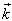 .
. | Figure 3. The elastic shell in the form of the terminal cylinder with the semi – spheres |
As was shown in [ 2, 4, 6, 3 ], the initial equation is integral equation , having the sense of the generalized Huygen’s principle, for the displacement vector 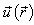 of the elastic shell:
of the elastic shell: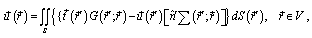 | (12) |
where 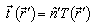 is the stress vector;
is the stress vector; 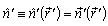 is the single vector of the external along the relation to S normal;
is the single vector of the external along the relation to S normal; 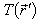 is the stress tensor of the isotropic material;
is the stress tensor of the isotropic material; 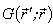 is the displacement Green’s tensor;
is the displacement Green’s tensor; 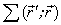 is the stress Green’s tensor; if
is the stress Green’s tensor; if 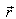 concerns to the point of the surface S, in the left part of the equation (12) will stand
concerns to the point of the surface S, in the left part of the equation (12) will stand 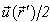 .The displacement vector
.The displacement vector 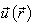 , the stress tensor
, the stress tensor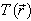 , the displacement Green’s tensor
, the displacement Green’s tensor 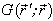 and the stress Green’s tensor
and the stress Green’s tensor 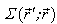 were connected between them selves by the following correlations[ 2, 7, 6, 3 ]:
were connected between them selves by the following correlations[ 2, 7, 6, 3 ]: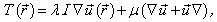 | (13) |
where 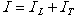 ;
; 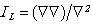 ;
; 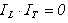 ;
;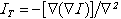 ,
, 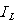 and
and 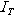 are the longitudinal and transverse single tensors for the Hamilton’s operator
are the longitudinal and transverse single tensors for the Hamilton’s operator 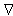 ;
;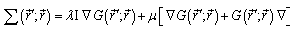 | (14) |
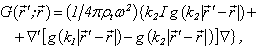 | (15) |
where k1 and k2 are the wave numbers of the longitudinal and transwerse waves in the material of the shell; 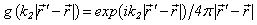 is the Green’s function.The second integral equation presents the Kirchhoff integral for the diffracted pressure
is the Green’s function.The second integral equation presents the Kirchhoff integral for the diffracted pressure 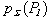 in the external medium[ 2, 7 ]:
in the external medium[ 2, 7 ]: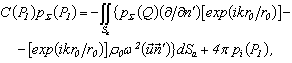 | (16) |
where 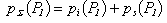 ;
; 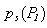 is the scattered pressure in the point P1; C(P1) is the numerical coefficient, equal 2π, if
is the scattered pressure in the point P1; C(P1) is the numerical coefficient, equal 2π, if 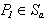 and 4π, if P1 out Sa; Sa is the external surface of the shell; Q is the point of the external surface of the shell.For the pressure
and 4π, if P1 out Sa; Sa is the external surface of the shell; Q is the point of the external surface of the shell.For the pressure 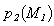 in the internal liquid medium in the point M1 is got the third integral equation:
in the internal liquid medium in the point M1 is got the third integral equation: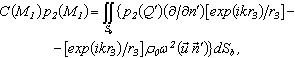 | (17) |
where 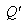 is the point of the inte;rnal surface of the shell;
is the point of the inte;rnal surface of the shell;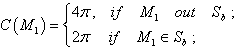 Sb is the internal surface of the shell.To the integral equations (12), (16) and (17) are added the boundary conditions on the external (Sa) and internal (Sb) surfaces of the shell:1) – at the both surfaces of the shell the tangent stresses are equally null:
Sb is the internal surface of the shell.To the integral equations (12), (16) and (17) are added the boundary conditions on the external (Sa) and internal (Sb) surfaces of the shell:1) – at the both surfaces of the shell the tangent stresses are equally null: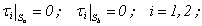 | (18) |
2) – the normal stress 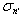 at the external surface of the shell is equally the diffracted pressure pΣ, but at the internal surface is equally the pressure p2
at the external surface of the shell is equally the diffracted pressure pΣ, but at the internal surface is equally the pressure p2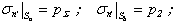 | (19) |
In the conformity with the conditions (18) and (19) the stress vector 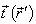 in the equation (12) is equal:
in the equation (12) is equal: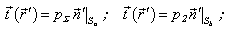 | (20) |
3) – the continuity of the normal component of the displacement at the both boundaries of the shell: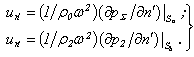 | (21) |
The substitution of the integral equations (17), (12) and (18) in the boundary conditions (18) – (20) gives the system of equations in terms of unknown functions pΣ, p2 and the components of the displacement vector 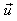 at the both surfaces of the shell. To obtain numerical solution of this system the integral equations are replaced the quadrature formulas and the grid of the nodal points is chosen at both surfaces of the shell as well as it has be done for the ideal non – analytical scatterers[2, 3].For choosing boundary conditions we will have the integrals of the two types: the integrals with the isolated special point and the integrals which are considered of the sence of the principal meaning. The method of the calculation of the second types was described in[2].
at the both surfaces of the shell. To obtain numerical solution of this system the integral equations are replaced the quadrature formulas and the grid of the nodal points is chosen at both surfaces of the shell as well as it has be done for the ideal non – analytical scatterers[2, 3].For choosing boundary conditions we will have the integrals of the two types: the integrals with the isolated special point and the integrals which are considered of the sence of the principal meaning. The method of the calculation of the second types was described in[2].
4. Conclusions
The method of integral equations is appearing effective by the study of the sound diffrac-tion on the ideal and elastic scatterers of the non – analytical forms. With the help of the this method and the integral equations Fredholm of the first and second kinds are calculating the angular distributions of the scattered pressure for the ideal non – analytical forms. At the basis of theory of the dynamics of the elastic bodies is solving the problem of the sound diffraction on the elastic scatterers of the non – analytical forms.
ACKNOWLEDGMENTS
This work was supported as part of research under State Contract no P242 of April 21, 2010, within the Federal Target Program “Scientific and scientific – pedagogical personnel of innovative Russia for the years 2009 – 2013”.
References
| [1] | H. Hoenl, A. Maue and K. Westpfahl, Theorie der Beugung, Berlin. Springer, 1961. |
| [2] | A. A. Kleshchev, Hydroacoustic Scatterers (Prima, St. Petersburg, 2012)[in Russian]. |
| [3] | A. A. Kleshchev, Tr. LKI “The Сommon Ship’s Systems” (1989), pp. 95 – 99. |
| [4] | A. E. Seybert , T. W. Wu and X. F. Wu X. F, J. Acoust. Soc. Am. 84, 1906 (1988). |
| [5] | A. A. Kleshchev, J. of Techn. Acoust. 2, 29 (1995). |
| [6] | J. S. Podstrigach, A. P. Poddubniak, Scattering of Sound Beams at Bodies of Spherical and Cylindrical Form (Naukova Dumka, Kiev, 1986)[in Russian]. |
| [7] | V. V. Varadan , V. R. Varadan , L. R. Dragonette, J. Acoust. Soc. Am. 84. 22 (1982). |
| [8] | A. A. Kleshchev, I. I. Klukin. Principles of Hydroacouctic. (Shipbuilding, Leningrad, 1987)[in Russian]. |
| [9] | A. A. Kleshchev. J. of Techn. Acoust. 2, 65 (1993). |
| [10] | A. A. Kleshchev. Scientific Worcs of RAO. 1, 240 (2005). |
| [11] | A. A. Kleshchev. Diffraction and Propagation of Waves in Elastic Mediums and Bodies. (Vlas, St.- Petesburg, 2002)[in Russian]. |
| [12] | A. A. Kleshchev. Diffraction, Radiation and Propagation of Elastic Waves. (Profprint, St.- Petersburg, 2006)[in Russian]. |
| [13] | A. A. Kleshchev. Phys. Acoust. 57, 381. (2011). |
| [14] | A. A. Kleshchev, E. I. Kuznetsova. Phys. Acoust. 57, 495 (2011). |
| [15] | A. A. Kleshchev. Phys. Acoust. 58, 338 (2012). |


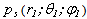 in the scattered wave in the point observation
in the scattered wave in the point observation 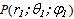 is equally[ 1, 2 ]:
is equally[ 1, 2 ]: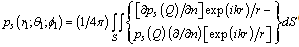
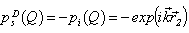 for the ideal hard scatterer ( the homogeneous Neimann’s condition):
for the ideal hard scatterer ( the homogeneous Neimann’s condition):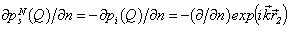 Then (1) for the Dirichlet condition at the surface is accepting the appearance:
Then (1) for the Dirichlet condition at the surface is accepting the appearance: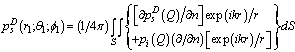
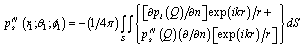
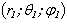 with the point of the surface scatterer
with the point of the surface scatterer 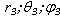 . Тhen (2) is transform in the Fredholm equation of the first kind for the function
. Тhen (2) is transform in the Fredholm equation of the first kind for the function 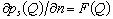 ( with the account of the Dirichlet condition):
( with the account of the Dirichlet condition):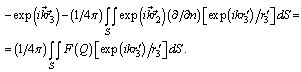
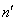 and are use the boundary Neimann’s condition, then we are get integro – differential equation for the funktion
and are use the boundary Neimann’s condition, then we are get integro – differential equation for the funktion 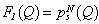 :
: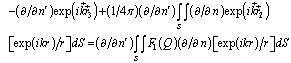
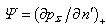 , where the sign «+» is mean the outside domain to S . For the Dirichlet condition th pressure pΣ is continuous by the crossing through the boundary S:
, where the sign «+» is mean the outside domain to S . For the Dirichlet condition th pressure pΣ is continuous by the crossing through the boundary S: 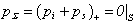 and
and 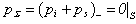 , while the function
, while the function 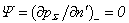 (since inside – the vacuum) , but outside -
(since inside – the vacuum) , but outside - 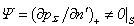 .The function
.The function 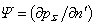 we are find from the solution of the non – homogeneous Fredholm equation of the second kind[ 1, 2 ]:
we are find from the solution of the non – homogeneous Fredholm equation of the second kind[ 1, 2 ]: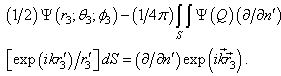
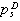 in the any point of the medium
in the any point of the medium 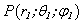 :
: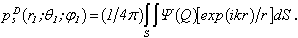
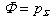 - the solution of the Fredholm equation of the second kind[ 1, 2 ]:
- the solution of the Fredholm equation of the second kind[ 1, 2 ]: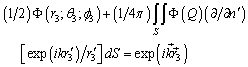 The scattered pressure in the point
The scattered pressure in the point 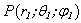 we are express through the function Ф:
we are express through the function Ф: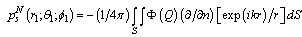
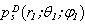 can find either with the help of the integral (2) (for the Fredholm equation of the first kind), or with the help of the equation (7) (for the Fredholm equation of the second kind).The surface S is consist of S2 and of the surfaces S1 и S3 (see fig. 1).For the calculation of the integrals (2) and (7) on surface
can find either with the help of the integral (2) (for the Fredholm equation of the first kind), or with the help of the equation (7) (for the Fredholm equation of the second kind).The surface S is consist of S2 and of the surfaces S1 и S3 (see fig. 1).For the calculation of the integrals (2) and (7) on surface 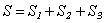 we are choose the grid of the nodal points. We are mark the nodal point through
we are choose the grid of the nodal points. We are mark the nodal point through 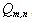 , where the index m is point out the room on the element, while the index n – on guide. The integrals (2) and (7) we are substitute the numerical quadratures
, where the index m is point out the room on the element, while the index n – on guide. The integrals (2) and (7) we are substitute the numerical quadratures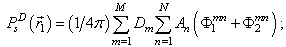
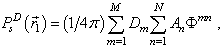
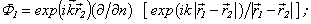
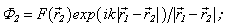
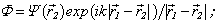
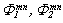 and
and 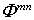 - the values of the functions Ф1, Ф2, and Ф in the nodal points Qmn; An, Dm – the weight coefficients; М – the quantity of the nodal points on the element, N – the quantity of the nodal points on the guide.The unknown functions
- the values of the functions Ф1, Ф2, and Ф in the nodal points Qmn; An, Dm – the weight coefficients; М – the quantity of the nodal points on the element, N – the quantity of the nodal points on the guide.The unknown functions 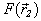 and
and 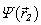 we are find from the solution of the Fredholm equation of the first kind (4) and of the Fredholm equation of the second kind (6).Transformed in (4) to the numerical quadratures, we are get the algebraice system of the equations of the order
we are find from the solution of the Fredholm equation of the first kind (4) and of the Fredholm equation of the second kind (6).Transformed in (4) to the numerical quadratures, we are get the algebraice system of the equations of the order 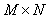 relatively Fmn – of the meanings
relatively Fmn – of the meanings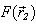 in nodal points:
in nodal points: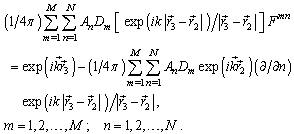
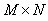 of the equations we transform to the system MN/2 (N – the even number), but by
of the equations we transform to the system MN/2 (N – the even number), but by 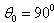 - to the system MN/4 (M and N - the even numbers). Easily see from fig. 1, that by
- to the system MN/4 (M and N - the even numbers). Easily see from fig. 1, that by 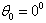 means of the function
means of the function 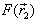 dependn’t on the angle
dependn’t on the angle 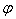 , that is
, that is 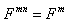 for everybody n = 1,2,…,N, and we get the system M – order. In correspondence with the integral of Kirchhoff the special point
for everybody n = 1,2,…,N, and we get the system M – order. In correspondence with the integral of Kirchhoff the special point 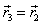 isolates in the equations (4). In the equation (6) the special point
isolates in the equations (4). In the equation (6) the special point 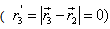 appearsn’t isolated, therefore the integral in the left part of the equation is considering in the meaning of the main value. For the calculation of this integral was using the following method. In the expression under the integral sign is appropriating the term of the simple analytical form, containing the singularity, which is integrating analytically. The staying part of the integral has the isolated special point and the corresponding integral is calculating by the help of the numerical method. The integral is showing in the kind of the three integrals:
appearsn’t isolated, therefore the integral in the left part of the equation is considering in the meaning of the main value. For the calculation of this integral was using the following method. In the expression under the integral sign is appropriating the term of the simple analytical form, containing the singularity, which is integrating analytically. The staying part of the integral has the isolated special point and the corresponding integral is calculating by the help of the numerical method. The integral is showing in the kind of the three integrals: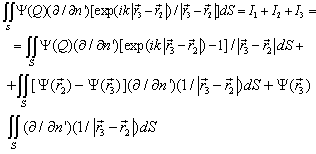
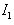 has not of the special point by
has not of the special point by 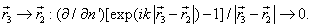 The integral
The integral 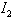 has the special point of the lesser kind and also is integrating by the numerical method.We cross to the calculation of the integral
has the special point of the lesser kind and also is integrating by the numerical method.We cross to the calculation of the integral 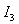 and consider firstly the integral:
and consider firstly the integral: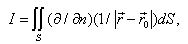
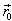 – the radius – vector of the point, which belongn’t to the surface S.From the Green’s formula is getting:
– the radius – vector of the point, which belongn’t to the surface S.From the Green’s formula is getting: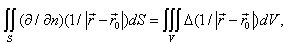 where V – the volume, limited on the surface S.We know, that:
where V – the volume, limited on the surface S.We know, that: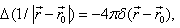 where
where 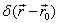 - delta function, satisfying to the relation:
- delta function, satisfying to the relation: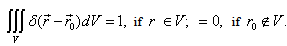 Therefore the integral I in (13) is equal:
Therefore the integral I in (13) is equal: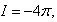 if the point is finding inside of the surface S and I=0, if is finding outside of the surface S. In the our version the point is finding on the surface S and the integral in the sense of the main meaning is equal:
if the point is finding inside of the surface S and I=0, if is finding outside of the surface S. In the our version the point is finding on the surface S and the integral in the sense of the main meaning is equal: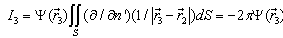
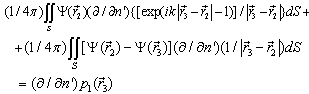
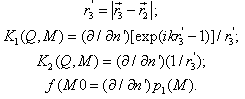 that the equation (15) has the form:
that the equation (15) has the form: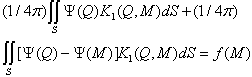
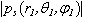 by the following parameters: a=1m, l=1m, ka=1, θ0 =
by the following parameters: a=1m, l=1m, ka=1, θ0 = 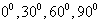 .At fig. 2-a and 2-b are present
.At fig. 2-a and 2-b are present 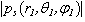 for the chosen parameters by θ0 =
for the chosen parameters by θ0 = 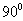 ( fig. 2-a) and θ0 =
( fig. 2-a) and θ0 = 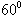 ( fig. 2-b) (the curve 1 corresponds to method of the T – matrixes, but the curve 2 – to the method of the integral equations).
( fig. 2-b) (the curve 1 corresponds to method of the T – matrixes, but the curve 2 – to the method of the integral equations).
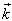 .
.
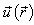 of the elastic shell:
of the elastic shell: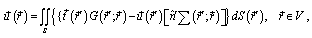
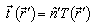 is the stress vector;
is the stress vector; 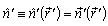 is the single vector of the external along the relation to S normal;
is the single vector of the external along the relation to S normal; 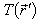 is the stress tensor of the isotropic material;
is the stress tensor of the isotropic material; 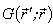 is the displacement Green’s tensor;
is the displacement Green’s tensor; 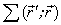 is the stress Green’s tensor; if
is the stress Green’s tensor; if 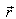 concerns to the point of the surface S, in the left part of the equation (12) will stand
concerns to the point of the surface S, in the left part of the equation (12) will stand 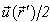 .The displacement vector
.The displacement vector 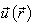 , the stress tensor
, the stress tensor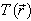 , the displacement Green’s tensor
, the displacement Green’s tensor 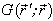 and the stress Green’s tensor
and the stress Green’s tensor 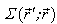 were connected between them selves by the following correlations[ 2, 7, 6, 3 ]:
were connected between them selves by the following correlations[ 2, 7, 6, 3 ]: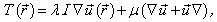
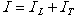 ;
; 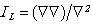 ;
; 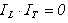 ;
;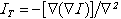 ,
, 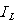 and
and 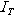 are the longitudinal and transverse single tensors for the Hamilton’s operator
are the longitudinal and transverse single tensors for the Hamilton’s operator 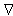 ;
;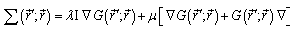
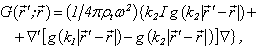
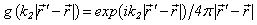 is the Green’s function.The second integral equation presents the Kirchhoff integral for the diffracted pressure
is the Green’s function.The second integral equation presents the Kirchhoff integral for the diffracted pressure 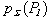 in the external medium[ 2, 7 ]:
in the external medium[ 2, 7 ]: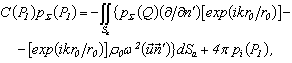
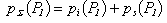 ;
; 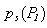 is the scattered pressure in the point P1; C(P1) is the numerical coefficient, equal 2π, if
is the scattered pressure in the point P1; C(P1) is the numerical coefficient, equal 2π, if 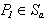 and 4π, if P1 out Sa; Sa is the external surface of the shell; Q is the point of the external surface of the shell.For the pressure
and 4π, if P1 out Sa; Sa is the external surface of the shell; Q is the point of the external surface of the shell.For the pressure 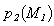 in the internal liquid medium in the point M1 is got the third integral equation:
in the internal liquid medium in the point M1 is got the third integral equation: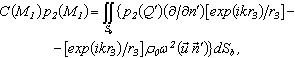
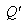 is the point of the inte;rnal surface of the shell;
is the point of the inte;rnal surface of the shell;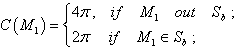 Sb is the internal surface of the shell.To the integral equations (12), (16) and (17) are added the boundary conditions on the external (Sa) and internal (Sb) surfaces of the shell:1) – at the both surfaces of the shell the tangent stresses are equally null:
Sb is the internal surface of the shell.To the integral equations (12), (16) and (17) are added the boundary conditions on the external (Sa) and internal (Sb) surfaces of the shell:1) – at the both surfaces of the shell the tangent stresses are equally null: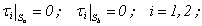
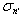 at the external surface of the shell is equally the diffracted pressure pΣ, but at the internal surface is equally the pressure p2
at the external surface of the shell is equally the diffracted pressure pΣ, but at the internal surface is equally the pressure p2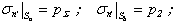
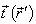 in the equation (12) is equal:
in the equation (12) is equal: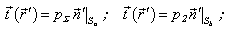
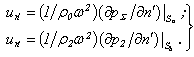
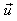 at the both surfaces of the shell. To obtain numerical solution of this system the integral equations are replaced the quadrature formulas and the grid of the nodal points is chosen at both surfaces of the shell as well as it has be done for the ideal non – analytical scatterers[2, 3].For choosing boundary conditions we will have the integrals of the two types: the integrals with the isolated special point and the integrals which are considered of the sence of the principal meaning. The method of the calculation of the second types was described in[2].
at the both surfaces of the shell. To obtain numerical solution of this system the integral equations are replaced the quadrature formulas and the grid of the nodal points is chosen at both surfaces of the shell as well as it has be done for the ideal non – analytical scatterers[2, 3].For choosing boundary conditions we will have the integrals of the two types: the integrals with the isolated special point and the integrals which are considered of the sence of the principal meaning. The method of the calculation of the second types was described in[2]. Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-Text HTML
Full-Text HTML