1. Introduction

During welding of stainless steels, local sensitized zones often develop. This is because of chromium carbide formation at grain boundaries, resulting in chromium depletion at regions adjacent to the grain boundaries [1-6]. Chromium depletion creates many local galvanic cells and if chromium content gets less than 12% wt., sensitivity to intergranular corrosion in the mentioned areas will occurs [7]. The sensitivity of austenitic stainless steels contain more than 0.05%wt. carbon is often due to heat affected zone and named weld decay[ 8, 9].Chromium has a very compositional tendency to carbon at 650-850℃; if austenitic stainless steel is held for more than the specific time at the above mentioned temperature range, carbon rich chromium carbides often in the form of M23C6 at austenite grains boundaries will be formed[8, 10]. Required sensitization time of stainless steels is usually shown as C-shape curves in which Carbon-Time- Temperature is being shown[11]. Sample of curves for stainless steel 304 has been shown in Figure 1[7]. Chemical composition, thermal cycle, internal or external stresses as well as service loadings; welding operations or previous transformation and the environment where the part is used are four main effective factors of sensitivity [10]. Analytical and numerical methods are used widely to investigate thermal and mechanical behaviour of welds. Rosenthal proposed the first process of analytical solution in welding which contained simplifying assumptions such as point heat source, constant thermophysical properties of material and steady-state heat flow[12]. Many computerized models have been proposed for studying two and three-dimensional heat flow during welding processes. In those models many of Rosenthal's numerical solution hypotheses have been changed; for instance, Kou et al.[13] studied the heat transfer during the welding of 3.2 mm thick 6061 aluminum sheet. Masubuchi et al.[14] utilized thermal analysis to study the residual stresses. Lee et al.[15] simulated the heat transfer in similar and dissimilar joints between structural steels. Teng et al.[16] investigated the effect of speed, sample dimension, external restraint and preheat on heat transfer and residual stresses. Taljat et al.[17] studied the heat flow and residual stresses in GTAW process and noticed the effects of solid-state transformations. Lu et al.[18] proposed a model to study current distribution, power and heat flow in GTAW welding process. Teng et al.[19] also suggested a model to evaluate the effect of sequence on the distribution of heat and residual stresses in SAW process. Despite the importance of weld decay phenomenon in austenitic stainless steels and its close relationship with thermal cycle, it seems that no numerical model has been proposed to study the relation of these phenomena yet. Therefore there is a need of an investigation these issues. This paper reports a thermal simulation of GTAW of austenitic stainless steel 304 to study chromium carbide precipitation and its relationship to welding parameters.

2. Experimental

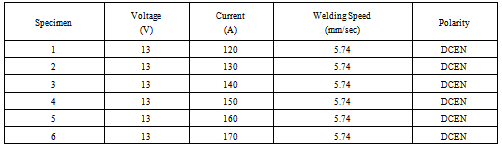
All Six 16080×3mm samples of stainless steel 304 were prepared; the surfaces were cleaned with acetone and bead-on-plate automatic GTAW welds without any filler metal were made at the centre of samples. Used physical and chemical properties of steel sheet were respectively according to the Tables 1 and 2. Applied welding parameters for the samples are in Table 3. The diameter of applied W-%2Th electrode was 1.6 mm, the internal diameter of ceramic nozzle was 12 mm, argon gas flow was 5 litre/minute and the arc length was 0.75 mm. Welding of all samples were done on a copper block, then transverse section at the centre of samples were prepared for macroscopic study. After usual metallographic stages in macrostructural revealing of sections, electroetch technique with %10 oxalic acid solution, voltage of 6 V and 15 second was used, photos of appeared sections were taken by utilizing stereograph microscope, and the optical microscope was used to calculate the distance of carbide band in all of the specimens.

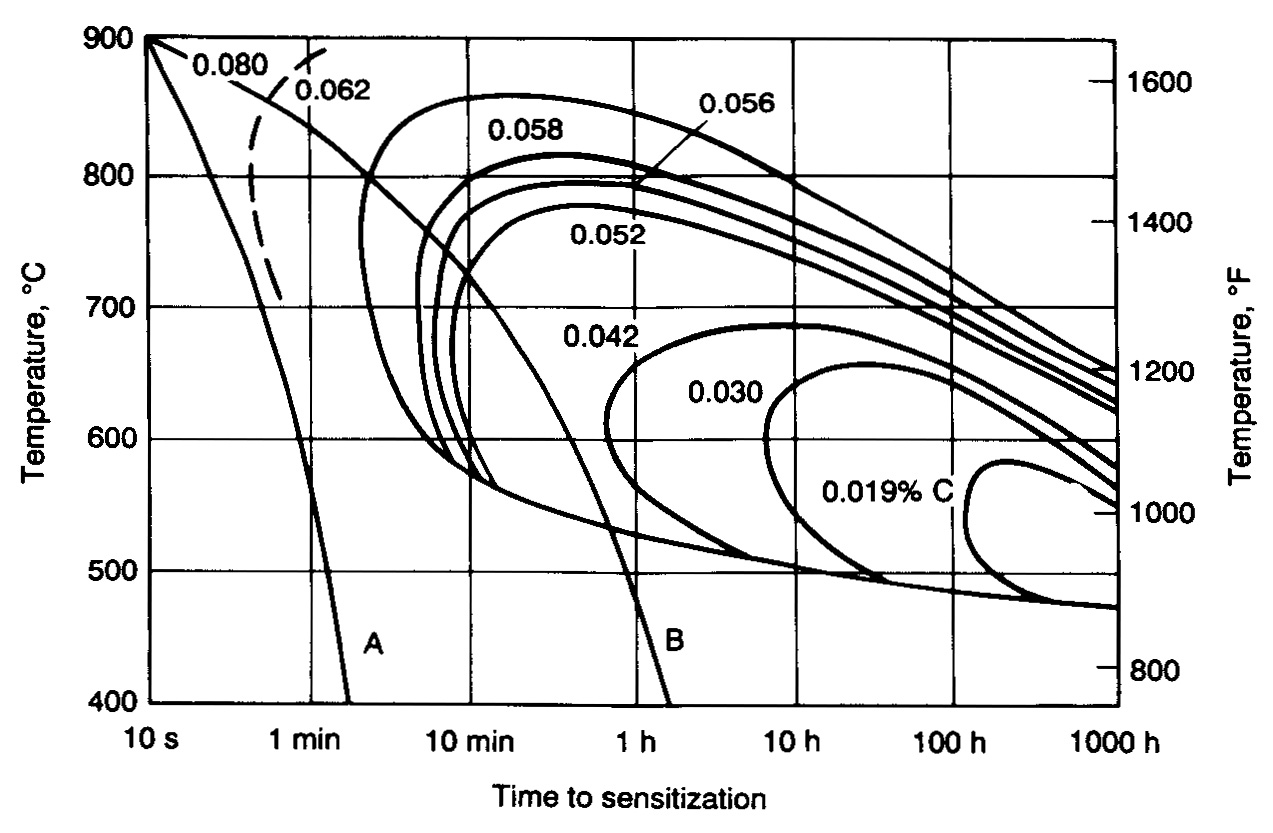Figure 1. Sample of time-temperature-sensitization curves for type 304 stainless steel in a mixture of CuSO4 and H2SO4 containing copper [7]

Table 1. Physical properties of stainless steel 304

Table 2. Chemical analysis of stainless steel 304

Table 3. Used welding parameters

3. Mathematical Model

Modelling of heat source is the most important point for thermal simulation of weld. The amount and the technique of heat distribution are effective factors for the size of weld pool and heat affected zone (HAZ). The amount of heat input from arc, heat distribution in the sample and the travel speed of heat source are the important parameters to formulate and modeling the heat source. Usual methods of source modeling in welding include: distribution of surface heat flux, distribution of volumetric heat flux and combination of above two mentioned models. The amount of heat given to the work piece in unit of time is being calculated according to equation (1):

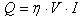(1)

In the above relation (I) is current intensity, (V) is voltage and (η) is arc efficiency. There are other factors such as kind of shielding gas, arc length, geometry of electrode, shape and dimensions of ceramic nozzle and type of work piece that affect on η[20].In welding with low current and high voltage, if the heat energy is assumed as surface thermal flux, satisfactory results will be obtained. Arc can mix up the surface of weld pool and affects the distribution of surface heat energy. According to Lu et al. currents more than 225A mix up the weld pool surface; it can assumed a flat free surface for weld pool at lower currents[18].In the present study, energy distribution of static arc with surface thermal flux is defined according to equation (2) in which the heat energy is assumed to be Gaussian:

(2)

In the above, (Q) is the welding input energy, (r) is the distance from the center of heat source and (r′) is the Gaussian distribution parameter [21]. The amount of η is set 0.6 in equation (1) and r' is set 1.5 mm. Finite element method and ANSYS software as well as two types of elements are used to analyse the model. To simulate the bulk model, SOLID90 (volume thermal element) was used and SURF152 (surface element) was utilized to simulate the surface heat flux. It is worth noting that in the finite element analysis, 3680 elements and 19220 nodes have been employed. Convection effects on the top and bottom surfaces of sheet considered with convection coefficients of h=15 W/ (m²K) for the surface in contact with air and h=800 W/ (m²K) for the surface in contact with copper sheet. Radiation of surfaces was abandoned and transient heat flow was analysed in different welding conditions. To account for heat transfer due to fluid flow in the weld pool, the thermal conductivity was assumed to increase linearly above the melting point by a factor of about three[17]. For modelling of heat source movement at time intervals, after applying heat on considered nodes, source was transferred to the front nodes. For solving the governing equations a finite element base program, ANSYS was employed. Equation 3 shows the governing heat conduction equation:

(3)

Where T is the temperature, K is the thermal conductivity, C is the specific heat, ρ is the density and Q is the rate of heat generation per unit volume (Q=0 for this case) and t represents welding time. Heat flux at the top surface is given by the equation 4 (as a boundary condition). The imposed boundary conditions are illustrated in Figure 2.

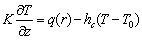(4)

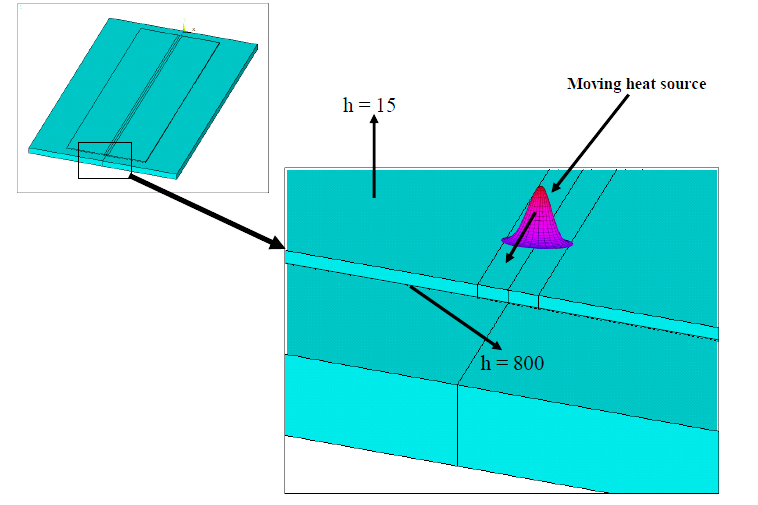Figure 2. Applied boundary conditions

4. Results and Discussion

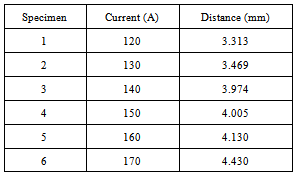
Figure 3 shows the meshed model and temperature distribution of the sample 4 obtained at three different time intervals. The results of finite element analysis for width of weld pools in different samples as well as obtained experimental results are compared in Table 4 and for instance, experimental and simulated weld section of sample 4 are shown in Figure 4. According to Table 4, increasing the current and resulted welding heat input causes weld pools dimensions will get greater.

One of the simulation results is time-temperature curves of different points. These curves can estimate the cooling rate and the staying time of different points around the weld pool in sensitization temperature range. To verify the model, precise formed carbide band zone near the surface of samples was investigated. The concerning results are shown in Table 5.

Table 4. Comparison of experimental and simulation results

Figure 3. (a) The meshed model; Temperature contours of specimen 4, (b) t=13.94 sec, (c) t=27.87 sec and (d) t=300

Figure 4. Comparison of experimental and simulated weld pool dimensions for specimen 4

Table 5. The precipitated distance of carbide band from weld pool center vs. current

Figure 5. Carbide band formation position for sample 3

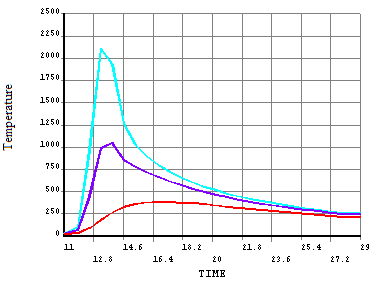Figure 6. Time-temperature curves of three points at the middle of sample 4 (A: x=4 mm, B: x=1 mm and C: x=8 mm)

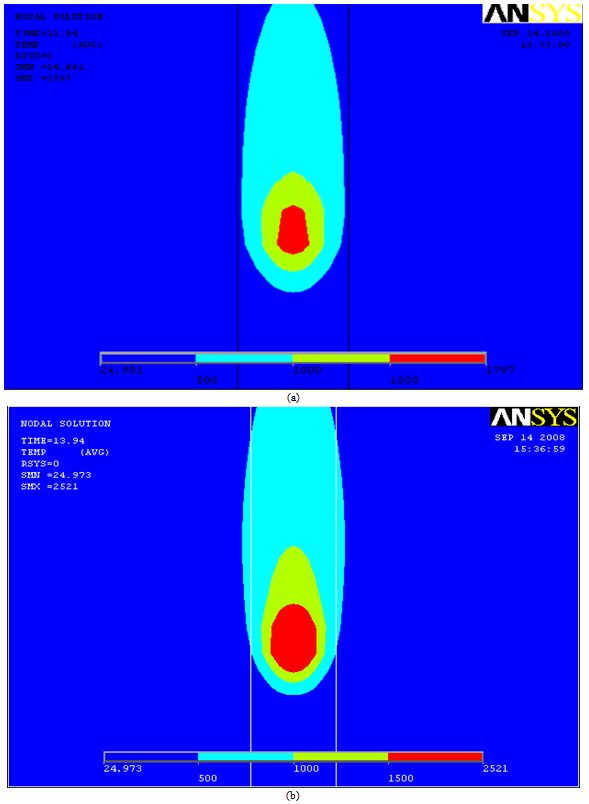Figure 7. Temperature Distribution; (a) in specimen 1 with I=120 A, (b) in specimen 6 with I=170 A

Also the position of the weld metal, base metal and carbide band is shown in Figure 5. Finite element model was used to obtain thermal history various points of any specimen. Time-temperature curves for three points on a line in the middle of specimen 4 with different distances from weld are shown in Figure 6. According to the C-shape curves at 650-850℃ which is sensitization range in austenitic stainless steel, a minimum maintenance time is needed for steel to be sensitized and chromium carbide to be precipitated at austenite grain boundaries. In these curves, according to the cooling rate of a point which is 4 mm far from weld (Curve A), needed time for carbide boundary formation is prepared and carbide precipitation is happened. For points with distances less than 4 mm in specimen 4 (Curve B), because of high cooling rate, the minimum time of boundary formation doesn't exist and even in points with greater distances than 4 mm (Curve C), carbide boundary doesn't form because points' temperature does not reach to maximum needed level. The effect of welding parameters on carbide boundary formation distance from the centre of weld pool is another important factor. Regarding the obtained results, with increasing welding heat input, the carbide band's distance is increased. When heat input is increased, the effective temperature range for chromium carbide to precipitate at austenite boundaries will be moved to farther distances relative to weld pool centre. For comparison, the effects of increasing the current and its effect on the temperature distribution in specimens 1 and 6 are shown in Figure 7.

5. Conclusions

In the present study a thermal model was developed to model heat transfer and carbide precipitation in welding of austenitic stainless steel 304. The results show that the proposed model has capability to predict the dimensions of weld pool and thermal history of different points of the welded samples and increasing the current results in the increased weld heat input and increased dimensions of weld pool. Since chromium carbide precipitation occurs at the specified temperature range, the developed finite element model can anticipate the occurrence area of this phenomenon. At a specific current, since the cooling rate of points adjacent to weld is increased and there is not enough time for the formation of chromium carbide, the phenomenon doesn't happen; at the farther points from weld line, the carbide band doesn't occur because of maximum temperature limit doesn't approach to 650-850℃ .When the current is increased and temperature distribution method is changed, sensitization temperature range will be moved to the further distances from weld line. Consequently, carbide band is formed at more distant regions and the current developed model anticipates this change easily. The possible future works are modeling of this phenomenon when filler metal is used and the effect of heat treatment on carbide precipitation.

ACKNOWLEDGEMENTS

The authors would like to thank Islamic Azad University, Ghiamdasht Branch for financial supporting.