1. Introduction

Similar to beams and plates, in many branches of engineering, cylindrical shells are the practical elements of various engineering structures such as pipes and ducts, bodies of cars, space shuttles, aircraft fuselages, ship hulls, submarines and construction buildings. However, analysing the dynamic characteristics of cylindrical shells is more complicated than that of beams and plates. This is mainly because the equations of motion of cylindrical shells combined with boundary conditions are more complex.

A comprehensive summary and discussion of shell theories including natural frequencies and mode shape information has been done by Liessa[1] in 1973. More recently, Amabili and Paidoussis[2], Amabili[3] and Kurylov and Amabili[4] have presented noteworthy reviews with a non-linear point of view. Many investigations followed the pioneering work of Love[5] using his first approximation theory, such as Flugge[6]. The Flugge theory is based on Kirchhoff-Love hypothesis for thin elastic shells. By using this theory, the strain-displacement relations and changes of curvatures of the middle surface of a cylindrical shell can be obtained. The simplified Donnell’s theory would be achieved by neglecting few terms in Flugge equations

Livanov[7] applied love’s assumption and useddisplacement functions to solve the problem of axisymmetrical vibrations of simply supported cylindrical shells. Rinehart and Wang[8] investigated the vibration of simply supported cylindrical shells stiffened by discrete longitudinal stiffeners using Donnell’s approximate theory, Flugge’s more exact theory and Love’s assumption for longitudinal wave numbers. Thesis theories are not only concerned with simply supported end conditions, but they have also applied other boundaries, such as cantilever cylindrical shells[9], fixed free circular cylindrical shells[10], clamped-clamped shells[11] and infinite length shells[12]. Most researchers and those cited above, use beam function as an approximation for the simply supported boundary conditions and find natural frequencies of vibration by the approximate method. This approximation is also useful for finite element analysis of cylindrical shells by using Hermitain polynomial of beam function type[13]. In addition to the approximate method, there are other approaches to find natural frequencies, like the computer based numerical method[14],[15] to avoid cumbersome computational effort and the wave propagation technique [16]. More recently Farshidianfar etl.[17] used the advantage of acoustical excitation to find natural frequency of long cylindrical shells.

Unlike beams or plates which are normally one or two dimensional structures, shells can freely vibrate in three directions. This has caused complicated the motions of the shell at resonance frequencies. Thus, apart from frequency behaviour, modal identification of cylindrical shells with their amplitudes has always been of great importance. Fields such as engineering design, acoustics and sound radiation are very much dependent on the amplitude ratios of cylindrical shells. Previous studies[18] have been made in order to identify amplitude ratios of the mode shapes, however, these studies are not complete.

In the present study, a semi-analytical approach is proposed to investigate the free vibration of simply supported cylindrical shells. As cited above, in traditional analysis, beam functions with similar boundary conditions are used to approximate wave numbers in the axial direction. This method is considered as an approximate technique. The approximate method is used to obtain the natural frequencies based on ten different shell theories (Donnell-Mushtari, Love-Timoshenko, Arnold-Warburton, Houghton-Johns, Flugge-Byrne-Lur’ye,Reissner-Naghdi-Berry, Sanders, Vlasov, Kennard-Simplified and Soedel). The results are also compared with experimental results and show good agreement. Finally, the behaviour of the circular shells with various aspect and thickness ratios was analysed. It was observed that by varying these parameters the dominant motion of the shell could change to either longitudinal, tangential or radial.

2. Theoretical Analysis

The cylindrical shell under consideration is with constant thickness h, mean radius R, axial length L, Poisson’s ratio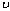, density 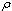and Young’s modulus of elasticity E. Here the respective displacements in the axial, circumferential and radial directions are denoted by 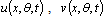and 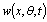as shown in Figure 1.

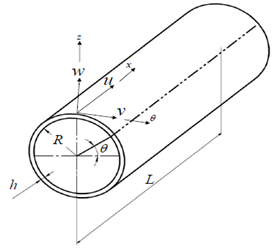Figure 1. Circular cylindrical shell: coordinate system and dimensions

In order to study free vibration of a cylindrical shell, the equations of motion can be written in matrix form as follows:

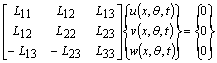(1)

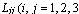where are differential operators with respect to 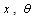, and t.

Different systems of equations are used to model the vibration behaviour of circular cylindrical shells. In this paper ten theories namely: 1) Donnell-Mushtari[1], 2) Love-Timoshenko[1], 3) Arnold-Warburton[1], 4)Houghton-Johns[1], 5) Flugge-Byrne-Lur’ye[1], 6)Reissner-Naghdi-Berry[1], 7) Sanders[1], 8) Vlasov[1], 9)Kennard-Simplified[1] and 10) Soedel[19], are used to find natural frequencies for various boundary conditions.

The first attempt in solving (1) is the assumption of a synchronous motion:

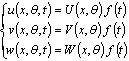(2)

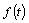where is the scalar model coordinate corresponding to the mode shapes 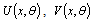and .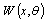

The next step is to use the separation of variables method in order to separate the spatial dependence of the modal shape between longitudinal and circumferential directions. Hence the axial, tangential and radial displacements of the wall vary according to:

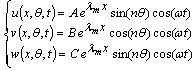(3)

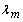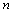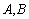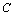in which and are the axial wavenumber and the circumferential wave parameter, respectively. and are the undetermined constants, and 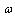is the circular frequency of the natural vibration.

Substituting (3) into (1), using any of the shell theories, leads to a set of homogenous equations having the following matrix form:

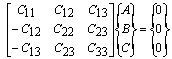(4)

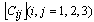in which are functions of and a frequency parameter that is defined as follows: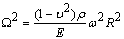

(5)

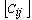The coefficient matrix, for the ten shell theories is obtained as follows:

Donnell-Mushtari

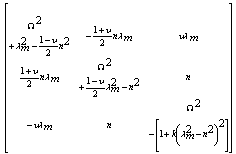(6)

Love-Timoshenko

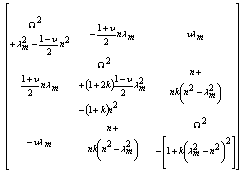(7)

Arnold-Warburton

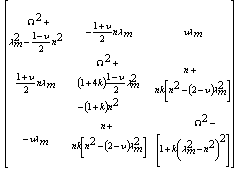(8)

Houghton-Johns

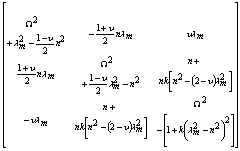(9)

Flugge-Byrne-Lur’ye

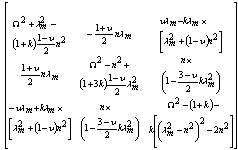(10)

Reissner-Naghdi-Berry

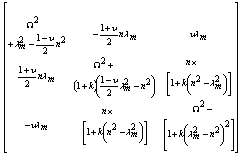(11)

Sanders

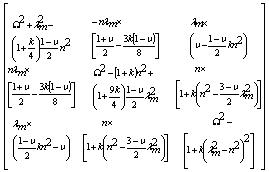(12)

Vlasov

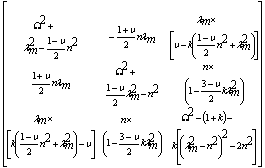(13)

Kennard-Simplified

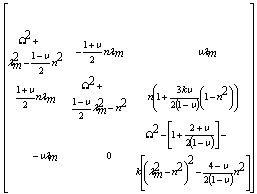(14)

For nontrivial solution the determinant of the coefficient matrix in (4) must be zero:

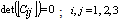(15)

The expansion of (15) will give the following two eigenvalue problems:

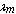• For a given value of there exists one or more proper values for 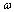so that the (15) vanishes.

• For a given value of there exists one or more proper values for 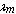so that the (15) vanishes.

Solving (15) leads to a cubic equation in terms of the nondimentioanl frequency parameter 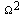. Thus for a fixed value of n and 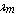, three positive roots and three negative roots are yield for the nondimensional frequency. The three positive roots are the natural frequencies of the cylindrical shell that can be classified as primarily axial, circumferential or radial. The lowest frequency is usually associated with a motion that is primarily radial (or flextural).

3. Beam Function Method

In general, solving the roots of the characteristic equation of (15) for 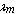is not possible in closed form. Hence, researchers have often leaned to use approximate techniques. Beam functions can be used to obtain natural frequencies and approximate displacements for closed circular cylindrical shells. This method is an assimilation of the flextural vibration of cylindrical shell with a transversely vibrating beam of the same boundary conditions. According to the approximate method, for a simply supported shell at both ends, the nature of the axial mode can be defined as:

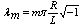(16)

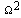By substituting (16) into (15), the only unknown of the characteristic equation will be the frequency parameter for a fixed combination of m and n.

4. Result and Discussion

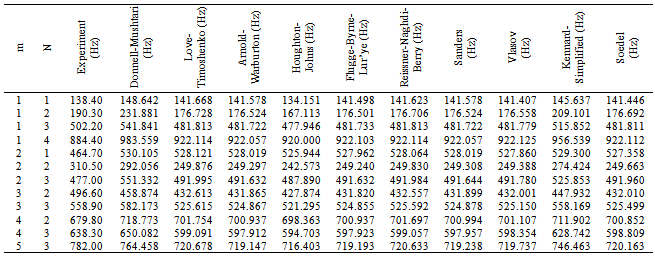
Since the beam function method is an approximation to obtain natural frequencies for thin circular cylindrical shells, it is important to check the accuracy of this method. Hence, the natural frequency for simply supported boundary conditions, calculated by using the beam functions via ten common theories of cylindrical shells.

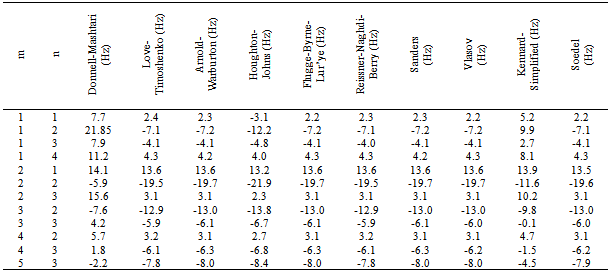
In Table 1, results calculated by the approximate method according to the ten theories, are compared with an experiment held by Farshidianfar etl.[17] for simply supported circular cylindrical shell. The shell investigated in Table 1 is made of aluminium with material properties; E=68.2GPa, ρ=2700 Kg/m³ and 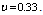The dimensions of the shell are: L=1.7272 m, R=0.0762 m and h=0.00147 m. The errors of all theories with respect to the experiment are also shown in Table 2. It is observed that, the beam function method yields close results compared to the experiment as well. It is also concluded that some theories (Love-Timoshenko, Arnold-Warburton, Flugge Byrne-Lur’ye, Reissner-Naghdi-Berry, Sanders, Vlasov, and Soedel) reveal same results. Kennard-Simplified, Reissner-Naghdi-Berry and Soedel are more accurate than the other theories and Dunnell-Mushtari and Houghton-Johns theory are not precise compared to other theories.

Let us now study the effects of length, radius and thickness on amplitude ratios and motions of the mode shapes of the shell. In Figures. 2-5 amplitude ratios are plotted as functions of the thickness ratio h/R, for shells with two aspect ratios L/R= 3 and 20.

According to Figurs.2-5 for L/R=3, nearly all modes up to m=3 have dominantly radial motions for all values of n, for shells of h/R<0.25. This is true except for 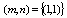, which also has an equally axial motion. It is observed that for shells of h/R>0.25 the axial and tangential motions become stronger, however, these type of shells are categorized into thick-walled shells. According to Love’s first approximation for thin-walled shells, only shells of small thickness to radius and length are categorized into thin-walled theories. Thus, it may not be exact to calculate shells of h/R>0.25 with thin-walled theories. However the general trend could be shown. Although, one would expect dominant radial motions for higher mode numbers of m, but, it is interesting that for m>3 modes and L/R=3, both amplitude ratios posses a quasi-sinusoidal and irregular behaviour. Therefore, shells with small L/R ratios have a complete irregular behaviour for different thicknesses at high mode numbers.

On the other hand, for L/R=20 a complete different pattern is observed compared to L/R=3. As reported in Figurs.2-5, for shells of L/R=20, at low mode numbers the tangential ratio behaves similar to a quasi-sinusoidal wave. However, the magnitude of the tangential and axial ratios does not exceed unity. Thus, the motions are always dominantly radial for long shells with small radius, regardless of the thickness.

Hence it is concluded from Figurs.2-5 that the thickness is a crucial parameter when dealing with short shells of small radius. This is due to the fact that, these types of shells behave similar to a ring rather than a beam.

Table 1. Comparison Between Approximation Analysis with Experimental Data

Table 2. Errors of the Ten Theories Compared with Experimental Data

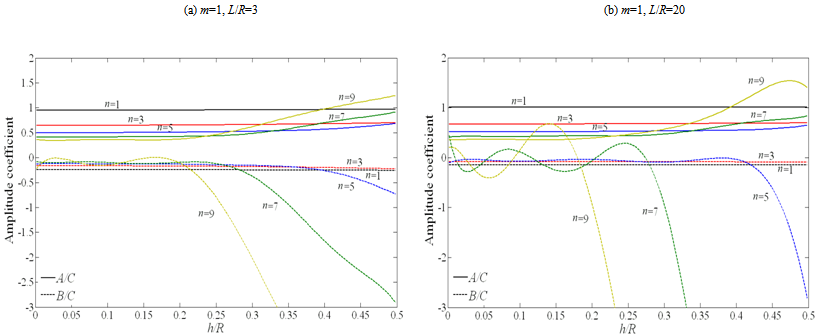Figure 2. Amplitude ratio versus h/R for m=1: (a) L/R=3; (b) L/R=20

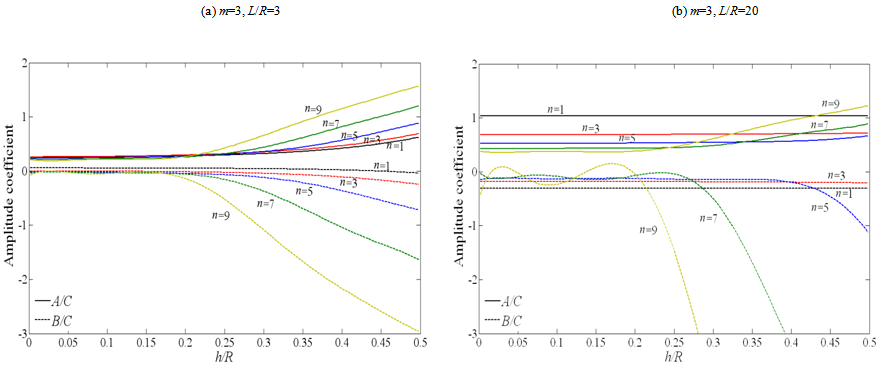Figure 3. Amplitude ratio versus h/R for m=3: (a) L/R=3; (b) L/R=20

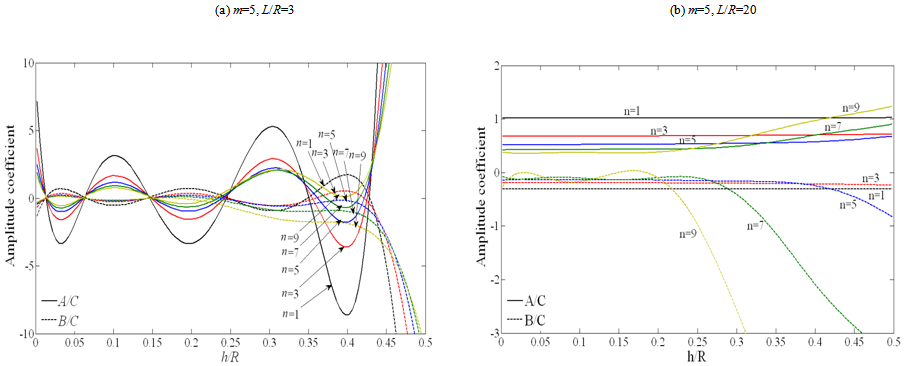Figure 4. Amplitude ratio versus h/R for m=5: (a) L/R=3; (b) L/R=20

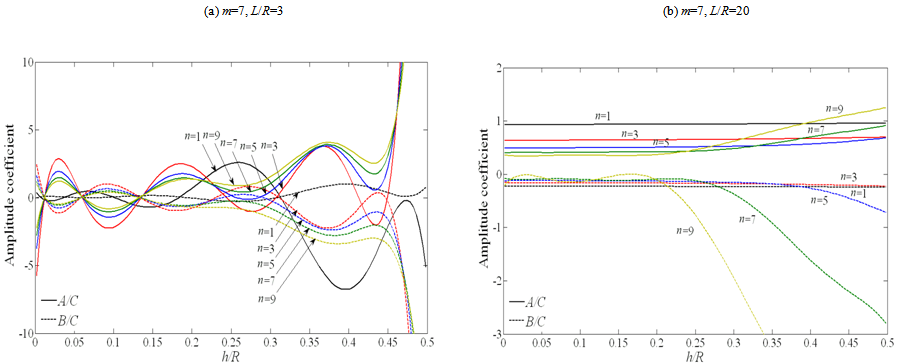Figure 5. Amplitude ratio versus h/R for m=7: (a) L/R=3; (b) L/R=20

5. Conclusions

The free vibration of circular cylindrical shells with simply supported boundary conditions has been studied using ten different thin shell theories: Donnell-Mushtari, Love-Timoshenko, Arnold-Warburton, Houghton-Johns, Flugge-Byrne-Lur’ye, Reissner-Naghdi-Berry, Sanders, Vlasov, Kennard-Simplified and Soedel. The scope of the investigation was focused upon using the beam function as an approximation for boundary condition to find the natural frequencies of a shell. Next, in order to check the accuracy of the theories, a comparison was carried out with experimental results and it shows good agreement. Moreover, theapproximate method based on the Soedel and Kennard-Simplified theories reviled better results compared to other theories.

Modal amplitudes which are important parameter in acoustical engineering were also analysed. The effects of length, radius and thickness are completely studied on amplitude ratios and mode shapes. Results show that both the aspect and thickness ratios are crucial parameters which can change the behaviour of a shell from beam type motion to ring type.