-
Paper Information
- Next Paper
- Previous Paper
- Paper Submission
-
Journal Information
- About This Journal
- Editorial Board
- Current Issue
- Archive
- Author Guidelines
- Contact Us
International Journal of Mechanics and Applications
p-ISSN: 2165-9281 e-ISSN: 2165-9303
2012; 2(5): 70-73
doi: 10.5923/j.mechanics.20120205.03
Damage Diagnostics in a Vertical Rod with Concentrated Masses on the Elastic Suspender
A. G. Khakimov
Institute of Mechanics, RAS Ufa Branch, Ufa, 450054, Russia
Correspondence to: A. G. Khakimov , Institute of Mechanics, RAS Ufa Branch, Ufa, 450054, Russia.
| Email: |  |
Copyright © 2012 Scientific & Academic Publishing. All Rights Reserved.
Investigations have been performed to identify natural frequencies of longitudinal vibrations in a notched vertical rod with concentrated masses on the elastic suspender. It has been obtained that dependencies of the rod’s circular longitudinal vibration frequencies on the notch coordinate have a periodic pattern. If the notch is located in the nodal point, the circular frequency of natural vibrations does not depend on the notch length. As shown, an increase in the mass of the lower load results in decreasing natural circular frequencies of the rod’s longitudinal vibrations. The research into the problem shows that it is possible to determine the coordinate and dimensions of a transverse notch in the vertical rod using three frequencies of free longitudinal vibrations.
Keywords: Sucker Rod, Vertical Sucker-Rod String, Concentrated Masses, Natural Frequencies of Longitudinal Vibrations, Notch Parameter, Length of Notch, Coordinate Of Notch
Article Outline
1. Introduction
- A sucker-rod string is the major component that limits pump unit reliability and working capacity in directional holes. A significant amount of failures in sucker-rod strings is caused by rod breaks. A rod break is supposed to be preceded by the formation of a portion with a smaller cross-sectional area. In case of a finite-length bar, a change in the natural frequency of longitudinal vibrations can be used to detect its defects[1]. In[2] the solution is given for determining the variable cross-sectional area along the longitudinal coordinate from the known dependence of the bar’s free-end displacement on the perturbing force frequency. In[3] and several other publications, a crack is simulated as a spring. A review of these studies is given in[4]. Different aspects of the problem are treated in[5, 6]. Paper[7] considers the solution to inverse problems on longitudinal travelling waves in finite-length bars.In[8], the author uses three natural longitudinal vibration frequencies and thus determines locality and dimensions of a transverse notch in a vertical rod stretched out by gravity and the force applied to its lower end.
2. Statement of the Problem
- Here we consider the stress-strain state of a straight rod fastened at its upper end to the elastic suspender with stiffness c1 and stretched out by gravity and concentrated masses M1 and M2 (Figure 1). The rod is assumed to have a short portion (as compared to its overall length) with a smaller cross-section area. This notch does not cause any rod bending and simulates its damage, specifically of the open-crack type. Consideration is given only to the stress-strain state within the elastic limit for a thin rod. Since the crack results from a small nucleus, not necessarily in the most stressed section, the notch is assumed to be found at any place along the rod’s length. The problem lies in determining the notch coordinate and dimensions relying on the approximation of the plane-section hypothesis.
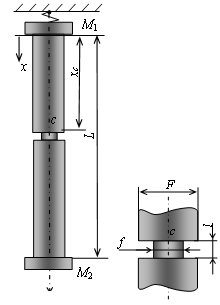 | Figure 1. The design scheme |
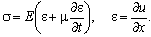 According to what has been said, we have
According to what has been said, we have 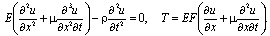 Let us measure the coordinate х from the fastening point and write down the boundary conditions
Let us measure the coordinate х from the fastening point and write down the boundary conditions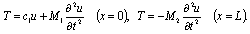 There is a complex spatial stress-strain state in and near the notch of short length l[9]. For the sake of simplicity, however, we assume uniaxial tension and compression. The experimental results[10] show that the mean value of the coefficient of longitudinal vibration attenuation in the notched rod under impact on its lower end is approximately 20 percent greater than the analogous coefficient for a non-notched rod. Let us consider the dynamic problem[1]
There is a complex spatial stress-strain state in and near the notch of short length l[9]. For the sake of simplicity, however, we assume uniaxial tension and compression. The experimental results[10] show that the mean value of the coefficient of longitudinal vibration attenuation in the notched rod under impact on its lower end is approximately 20 percent greater than the analogous coefficient for a non-notched rod. Let us consider the dynamic problem[1]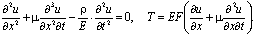 | (1) |
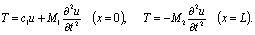 | (2) |
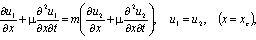 | (3) |
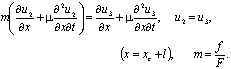 | (4) |
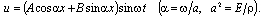 Six constants In this solution written down for the domains 0 ≤ х ≤ хс, хс ≤ х ≤ хс1, хс1 ≤ х ≤ L (хс1 = хс + l) are determined from six boundary conditions (2)-(4). In order for Ai, Bi (i=1÷3) not to be simultaneously zero, the following determinant should equal zero
Six constants In this solution written down for the domains 0 ≤ х ≤ хс, хс ≤ х ≤ хс1, хс1 ≤ х ≤ L (хс1 = хс + l) are determined from six boundary conditions (2)-(4). In order for Ai, Bi (i=1÷3) not to be simultaneously zero, the following determinant should equal zero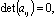 | (5) |
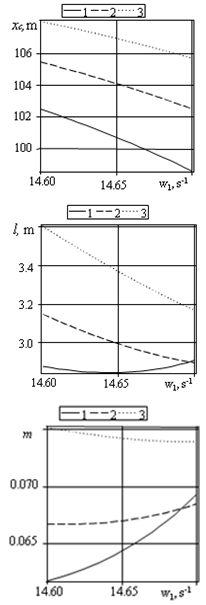
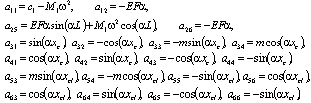 Condition (5) gives a frequency equation not presented here because of its awkwardness.When the coefficient is c1 → ∞, the frequency equation simplifies. For the non-notched rod without concentrated masses it follows from the frequency equation that cos αL = 0 and natural frequencies equal[1] αL = (2k – 1)π/2 (k = 1, 2, …) or ωk = (2k – 1)πa/2L.The determination of m, l and xc calls for an analysis of natural longitudinal vibration frequencies in the notched rod to be done.
Condition (5) gives a frequency equation not presented here because of its awkwardness.When the coefficient is c1 → ∞, the frequency equation simplifies. For the non-notched rod without concentrated masses it follows from the frequency equation that cos αL = 0 and natural frequencies equal[1] αL = (2k – 1)π/2 (k = 1, 2, …) or ωk = (2k – 1)πa/2L.The determination of m, l and xc calls for an analysis of natural longitudinal vibration frequencies in the notched rod to be done.3. Primal problem
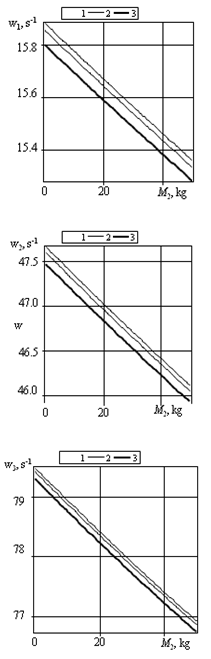
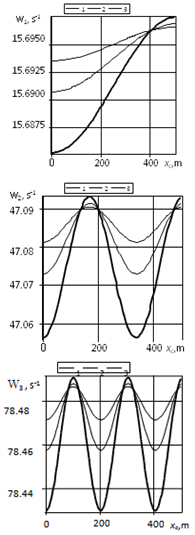 | Figure 2. Dependences of the rod’s circular longitudinal vibration frequencies ω1, ω2, ω3 on the notch coordinate xc for the parameter m=0.1 and different lengths l (curve 1−0.01, 2−0.02, 3−0.04 m) |
4. Inverse Problem
5. Conclusions
- Dependencies of the rod’s circular longitudinal vibration frequencies on the notch coordinate have a periodic pattern. If the notch is located in the nodal point, the circular frequency of natural vibrations does not depend on the notch length. An increase in the mass of the lower load results, at a given notch coordinate, in decreasing natural circular frequencies of the rod’s longitudinal vibrations. The coordinate and dimensions of a transverse notch in the vertical rod hanged on the elastic suspender and stretched out by gravity and concentrated loads are determined using three frequencies of free longitudinal vibrations.The obtained results can be recommended for diagnosing damages in sucker-rod strings.
ACKNOWLEDGEMENTS
- The investigation was financially supported by the Russian Foundation for Basic Research (Projects 11-01-97003-r_povolzhie_а, 11-01-00293_а).
 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-Text HTML
Full-Text HTML