Valeh I. Bakhshaliev
Azerbaijan Technical University, H. Javid Avenue 25, Baku, AZ1073, Azerbaijan
Correspondence to: Valeh I. Bakhshaliev , Azerbaijan Technical University, H. Javid Avenue 25, Baku, AZ1073, Azerbaijan.
| Email: |  |
Copyright © 2012 Scientific & Academic Publishing. All Rights Reserved.
Abstract
The decision of contact problems taking into account the wear process of nano- and macro-surfaces of sliding bearings of piston machines has great importance for forecasting their durability. Wear processes of the surfaces create tension change on the contact area. The paper focuses on the mathematical modelling of the wear process of the insert of sliding bearings made of self-lubricating material, taking into account contact deformation using the elements of nanomechanics. The differential equation of a contact condition of this bearing is deduced and solved. A method is developed to define the intensity of the wear of the insert of sliding bearings made of self-lubricating material. There is determined the expression for definition of dimensionless parameters of speed of wear of the surface of the insert of sliding bearing. The method developed for estimation of intensity of the wear process allows us to operate this process and to find the optimum value of wear of mobile couplings of sliding bearings.
Keywords:
Friction and Wear, Sliding Bearing, Engineering and Contact Mechanics, Strength of Materials, Nanomechanics, Self-lubricating Materials
1. Introduction
Sliding bearings (SB) are one of the important links of modern piston machines and mechanisms used at oil and gas industry. SB operate in the conditions of relative sliding of a surface of a shaft on a surface of the insert of the bearing and are a type of heavy loaded joint [1-3].Bearings and hinged connections of the piston machines applied at oil and gas industry are exposed to the greatest pressure and deterioration. Thus specified bearings are worked under the action of variable loading and during operation there are to take place the difficult processes of weariness and destruction. The friction and wear process in bearings and hinges reduce accuracy and efficiency of piston machines, lead to loss of working capacity of the mechanism and cause vibration, noise and impact of details. For estimation of a friction force, an intensity of wear process, a mechanical losses of these machines, it is necessary to know dependences of these parameters with respect to many factors, namely physical and chemical properties of a material, loading, their kinematics, thermodynamics and lubrications.It is recommended to apply self-lubricating materials for the manufacturing of critical SB parts working in extreme conditions. Selection of self-lubricated materials for SB has important scientific and practical value for their reliable work. These bearings are produced on the basis of porous of the iron and bronze, the aluminum and graphite by method of powder metallurgy. The work of SB in a self-lubricating regime is provided at the expense of the lubrication which is in pores of sintered material which is impregnated after sintering. They possess advantages for working in places too remote for lubrication. In the given conditions, self-lubricated sliding bearings can work in a regime of boundary friction.Self-lubricating materials can successfully apply in friction links of machines and mechanisms in mechanical engineering and oil industry. They are a new class of materials for the frictional links, possessing ability to create on friction surfaces the focused films having small durability and maintaining a great number of cycles of loading without destruction. In the friction processes the film is continuously created and supported, and arising deformations are localised in a thin layer. The temperature regime of these materials depending on working function, fluctuates within 200 - 1100°С [4, 5].Solving contact problems while taking into account the wear process of self-lubricating nano- and macro-surfaces has great value for forecasting SB durability. Their operational properties are defined basically by selection of materials, service conditions (friction regime, range of working temperatures), wear resistance of a material, etc. Wear processes of SB create tension change on the contact area. But the tension change in turn affects the intensity of the wear process, i.e. wear process is a process with feedback. For the estimation of a wear process in SB, contact problems of the theory of elasticity are used, taking into account the wear of details [6-9, 13].The wear process of the SB insert made of self-lubricated materials is mathematically modeled, taking into account contact deformation of the nanosurfaces of the shaft and insert.
2. Problem Formulation and the Method of Solution
The decision of this problem is complicated by a great number of parametres. As it is known that capacity and mechanical losses in machines on overcoming of friction forces, first of all, depend on speed and loading of kinematical pairs, quantity and quality of lubrications, size of clearances in these pairs and other factors.| Table 1. The numerical values of N and β depends on crank rotation angle α |
| | α | N, N | β | | 0˚ | 7449 | 4˚20` | | 15˚ | 893 | 173˚ | | 30˚ | 21487 | 174˚ | | 45˚ | 30338 | 171˚ | | 60˚ | 32333 | 163˚ | | 75˚ | 28345 | 165˚ | | 90˚ | 25483 | 162˚ | | 105˚ | 24239 | 161˚ | | 120˚ | 31326 | 165˚ | | 135˚ | 15861 | 162˚ | | 150˚ | 7218 | 154˚ | | 165˚ | 2780 | 33˚ | | 180˚ | 4626 | 5˚ | | 195˚ | 15215 | 4˚ | | 210˚ | 34731 | 6˚ | | 225˚ | 32129 | 6˚ | | 240˚ | 24703 | 5˚ | | 255˚ | 15830 | -0˚40` | | 270˚ | 13676 | -3˚ | | 286˚ | 21365 | 5˚ | | 300˚ | 17092 | 4˚ | | 315˚ | 13324 | 1˚20` | | 330˚ | 10051 | 0˚15` | | 345˚ | 8991 | 1˚ | | 360˚ | 8515 | 4˚ |
|
|
The reliable and durable operation of machines and mechanisms in large degree determined by the functioning of the bearing assemblies. The problem of the research of a friction and wear process of the main shaft and bearings is one of the important problems of the piston machines.Durability of the sliding bearings depends on the appointment of machines. It should be noted that at loading reduction twice the durability of work of the bearing increases almost in 10 times.The wear process of the insert of the main sliding bearings under action of the variable force N is characteristic of piston machines was considered in this work. Reference [10] presented a technique for determining the variable forces N that act on the journal of shaft of a vertical piston-type compressor and found the numerical values of the forces N and angle of rotation of the contact point β as a function of the crank rotation angle α. The Table 1 presents the numerical values of N and β depends on crank rotation angle α.On the basis of data in this Table, the Fig. 1 and 2 shows the curves of the dependence of the force N and the angular velocity 𝝎 of the motion of the contact point of the shaft journal and insert of the bearing with respect to the crank rotation angle, where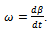 .
.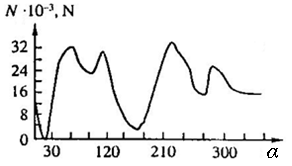 | Figure 1. The curve of the dependence of the force N with respect to the crank rotation angle |
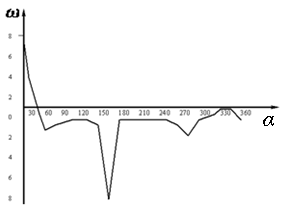 | Figure 2. The curve of the angular velocity 𝝎 of the motion of the contact point with respect to the crank rotation angle |
The SB insert with an eccentrically located axle journal of a shaft is shown in Fig.3, where O is the centre of the insert of the bearing, O1 is the centre of the journal of the shaft, C is the middle point of the contact surface and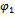 is the angle between the central axis OO1C of the contact surface and vertical axis Oy. We will choose the Oxyz Cartesian system of coordinates, an axis z which is directed along an insert axis, and x and y on the insert plane. Assume that the wear process occurs on a plane Oxy. Neglecting the wear process along axis z, the equation of a surface of the insert will be:
is the angle between the central axis OO1C of the contact surface and vertical axis Oy. We will choose the Oxyz Cartesian system of coordinates, an axis z which is directed along an insert axis, and x and y on the insert plane. Assume that the wear process occurs on a plane Oxy. Neglecting the wear process along axis z, the equation of a surface of the insert will be: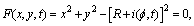 | (1) |
where R is the initial radius of the internal surface of the insert, x and y - coordinates of a point on this surface, 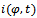 is the linear value of the wear of the insert, and φ is the angle between the radius-vector of any point K of a surface and a vertical axis y.
is the linear value of the wear of the insert, and φ is the angle between the radius-vector of any point K of a surface and a vertical axis y.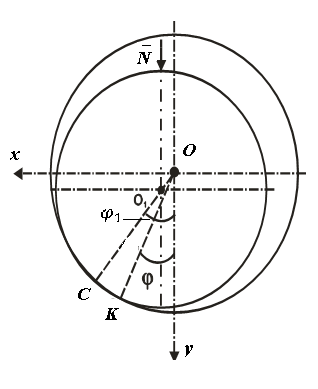 | Figure 3. The internal surface of sliding bearing with eccentrically located axle of a shaft |
 | Figure 4. The kinematic pair of an axle journal of a shaft and insert of sliding bearing with acting forces |
The coordinates x and y are defined from Fig. 3: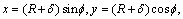 | (2) |
where 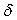 is the displacement of the centre of an axle journal of a shaft.It should be noted that the dimensionless characteristics of the wear process are rather convenient for comparison of wear resistance of self-lubricating materials of SB. The following variable parameters we denote by the following dimensionless symbols:
is the displacement of the centre of an axle journal of a shaft.It should be noted that the dimensionless characteristics of the wear process are rather convenient for comparison of wear resistance of self-lubricating materials of SB. The following variable parameters we denote by the following dimensionless symbols: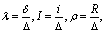 | (3) |
where 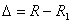 - a radial clearance,
- a radial clearance, 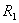 - radius of an axle journal of a shaft.Taking into account (2) and (3), from expression (1) it is found:
- radius of an axle journal of a shaft.Taking into account (2) and (3), from expression (1) it is found: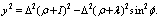 | (4) |
Differentiating (4), after some calculation we will receive: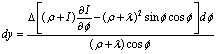 | (5) |
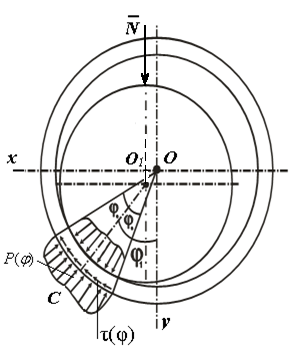
Fig. 5 shows the kinematic pair of an axle journal of a shaft an insert of SB with operating forces on a shaft. These forces are the following: N - the force pressing a shaft to the bearing, 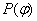 - the contact pressure of the insert acting on a shaft, and τ(φ) is the tangential stresses in the contact surface. Here
- the contact pressure of the insert acting on a shaft, and τ(φ) is the tangential stresses in the contact surface. Here 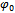 is half of the contact surface angle. We allot the nanoparticle (element K in Fig. 3) of the insert of the SB. In Fig. 3 this element is shown with the forces acting on it. Let’s make a condition of balance of an element K, corresponding to the central angle
is half of the contact surface angle. We allot the nanoparticle (element K in Fig. 3) of the insert of the SB. In Fig. 3 this element is shown with the forces acting on it. Let’s make a condition of balance of an element K, corresponding to the central angle 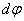 , in the following form:
, in the following form: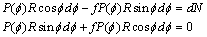 | (6) |
where dN is the elementary normal load acting on the element K, and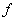 is the coefficient of friction between the axle journal and insert of SB.
is the coefficient of friction between the axle journal and insert of SB.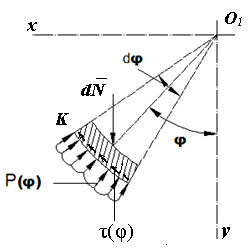 | Figure 5. The nanoelement of the insert of sliding bearing with acting forces |
From the first equation of (6) it is found: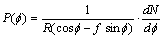 | (7) |
The condition of contact of bodies is written thus: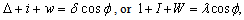 | (8) |
where w – elastic displacement of an element of surface of the insert and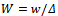 .In work [11] the expression for definition of the elastic displacement of internal surfaces of the insert of SB is deduced, which in our case it becomes:
.In work [11] the expression for definition of the elastic displacement of internal surfaces of the insert of SB is deduced, which in our case it becomes: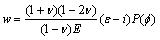 | (9) |
where 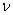 is the coefficient of Poisson, E is the modulus of elasticity, and
is the coefficient of Poisson, E is the modulus of elasticity, and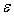 is the thickness of a self-lubricated surface of the insert.Let’s enter a symbol:
is the thickness of a self-lubricated surface of the insert.Let’s enter a symbol: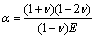 | (10) |
Substituting the expressions (9) and (10) to the (8), we will receive: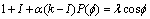 | (11) |
where 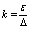 .The boundary conditions of a given task are:
.The boundary conditions of a given task are: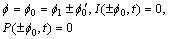 | (12) |
where 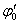 is a contact angle, and
is a contact angle, and  is an angle of displacement of the contact zone with respect to the vertical axis.Substituting the boundary conditions (12) to the equation (11), we receive:
is an angle of displacement of the contact zone with respect to the vertical axis.Substituting the boundary conditions (12) to the equation (11), we receive: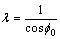 | (13) |
On the basis of Hook’s law, we can write: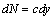 | (14) |
where c is the coefficient of elasticity of the material of the insert.Substituting the expression (7) into (11) while taking into account (5), (13) and (14), after some calculations we receive the differential equation of the contact condition of SB in dimensionless parameters: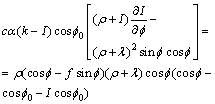 | (15) |
To solve of the differential equation (15) we will attach to it the boundary conditions (12).On the basis of a method of harmonious balance, to solve the differential equation (15) we will search the solution of this equation in the form of the trigonometric series [7]: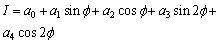 | (16) |
where 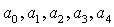 are the unknown factors which are subject to definition.Having substituted expression (16) and its derivative into the equation (15) we receive the following identity:
are the unknown factors which are subject to definition.Having substituted expression (16) and its derivative into the equation (15) we receive the following identity:
 Having equated the coefficients at the
Having equated the coefficients at the 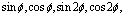 and also a free member we will have the corresponding algebraic equations. After some calculation and simplification these equations will become:
and also a free member we will have the corresponding algebraic equations. After some calculation and simplification these equations will become: | (17) |
From five algebraic equations (17), containing five unknown parameters а0, а1, а2, а3, а4 we find these unknown factors. Having substituted these factors into (16) we find the expression for definition of dimensionless parameters of intensity of wear of the surface of the SB insert.Change of the stress condition in the contact zone, caused by degeneration of plastic deformations in elastic, will be accompanied by an increase of contact between the surfaces of the shaft and the insert of SB, i.e. will be accompanied by increase of clearances in SB [8, 12, 14].Change of the form of a surface of the SB insert is characterised by velocity of the wear process . The velocity of the wear process, taking into account expressions (3) and (16), is defined as:
. The velocity of the wear process, taking into account expressions (3) and (16), is defined as: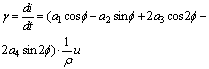 | (18) |
where u – is the relative velocity of sliding, here 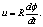 It is necessary to notice that in the SB at the motionless insert and a shaft rotating with constant angular velocity, the velocity of relative sliding of the points of a surface of the insert located in the field of contact will be a constant.One of the important parameters of contact problem of SB is the parameter
It is necessary to notice that in the SB at the motionless insert and a shaft rotating with constant angular velocity, the velocity of relative sliding of the points of a surface of the insert located in the field of contact will be a constant.One of the important parameters of contact problem of SB is the parameter 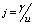 , named the intensity of wear process.From (18) it follows that
, named the intensity of wear process.From (18) it follows that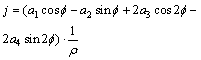 | (19) |
Thus, the expression (19) for definition of intensity of the wear process of the insert of SB made of self-lubricating material, taking into account the basic constructive, technological and operational characteristics of SB, is deduced.The method developed for estimation of intensity of the wear process of SB allows us to operate the wear process of the bearing. Researcher has shown that at intensive wear process of the mobile interface of SB, at a certain clearance size the dynamic loading, vibration and noise that influence its durability start to increase considerably. On the basis of the above method, it is possible to define the optimum value of the wear process and clearances in sliding bearings at which no disruption will be caused in its reliable work.
3. Conclusions
1. The expressions for definition of intensity of the wear process of an insert of a sliding bearing made of self-lubricating material are deduced.2. The developed method allows the optimum value of wear of mobile couplings of sliding bearings to be defined.3. Research results can be useful for development and operation of sliding bearings with a surface covering of self-lubricating material.4. The method developed for estimation of intensity of the wear process allows to operate this process and can be useful at the calculation of the sliding bearings on the durability.
ACKNOWLEDGEMENTS
This work was supported by the Science Development Foundation under the President of the Republic of Azerbaijan- Grant No EIF/BGM-1-BS-ERA-NET-2010/2011
References
| [1] | Bakhshaliev V.I. Mechanics of Piston Machines. – Lambert Academic Publishing, Germany, 2011. |
| [2] | Rangwala A.S. Reciprocating Machinery Dynamics, New Age International Publishers, Delhi, 2006. |
| [3] | Liong R.T., Proppe C. Application of a Cohesive Zone Model for the Investigation of the Dynamic Behavior of a Rotating Shaft with a Transverse Crack. Proc. 8th IFToMM International Conference on Rotordynamics 12.-15.09, Seoul, Korea, 2010. |
| [4] | Yanovsky Yu.G., Zgaevskii V.E. Mechanical properties of high elastic polymer matrix composites filled with rigid particles: Nanoscale consideration of the interfacial problem. Composite Interfaces, v.11, N3, pp.245-261, 2004. |
| [5] | Vakhrouchev A.V. Computer simulation of nanoparticles formation, moving, interaction and self-organization. Journal of Physics: Conference Series. V. 61. pp..26-30, 2007. |
| [6] | Galin L.A. Contact problems of the theory of elasticity and viscoelasticity. Moscow, “Science” publishing house, 304 pp. 1980. (in Russian) |
| [7] | Bakhshaliev V.I. The Problem of Mathematical Simulation of Rolling Friction, Journal of Friction and Wear, 2009, Vol. 30, No. 5, © Allerton Press, Springer, Inc., pp. 305–308, 2009. |
| [8] | Goryacheva I.G., Dobychin M.N., Soldatenkov I.A., Bogdanov V.M., Zakharov S.M. Simulation of Wheel/Rail Contact and Wear in Curved Track, Proceeding of International Heavy Haul Association Conference ‘‘Wheel-Rail Interface’’, Vol.1, pp. 215-220, 1999. |
| [9] | Popov V.L. Contact Mechanics and Friction. Physical principles and applications. Springer-Verlag, Berlin, Heidelberg, 2010. |
| [10] | Bakhshaliev V.I. Analysis of the accuracy of the crank-slider mechanism of piston machines with clearances. J. Machinery manufacture and reliability, No.3, pp. 1-4, Allerton Press, Inc. 2004. |
| [11] | Galakhov M.A, Usov P.P. Differential and integral equations of the mathematical theory of a friction. – Moscow, “Nauka” publishing house, 1990. (in Russian) |
| [12] | Davitashvili N. Mgebrishvili N. etc. Dynamic investigation of hinged mechanisms by taking into account wear and clearances in kinematics pears. Inter. S. J. “Problems of Applied Mechanics”. Tbilisi, N 4(25), pp. 47-57, 2006. |
| [13] | Hetzler H. On the influence of contact mechanics on friction induced flutter instability. In Proc. in Applied Mathematics and Mechanics (PAMM), 2009, Volume 9, Number 1, p. 275-276 |
| [14] | Boyaci A., Seemann W., Proppe C. Nonlinear stability analysis of rotor-bearing systems. In Proc. in Applied Mathematics and Mechanics (PAMM), 2009, Volume 9, Number 1, p. 279-280 |

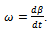 .
.

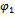 is the angle between the central axis OO1C of the contact surface and vertical axis Oy. We will choose the Oxyz Cartesian system of coordinates, an axis z which is directed along an insert axis, and x and y on the insert plane. Assume that the wear process occurs on a plane Oxy. Neglecting the wear process along axis z, the equation of a surface of the insert will be:
is the angle between the central axis OO1C of the contact surface and vertical axis Oy. We will choose the Oxyz Cartesian system of coordinates, an axis z which is directed along an insert axis, and x and y on the insert plane. Assume that the wear process occurs on a plane Oxy. Neglecting the wear process along axis z, the equation of a surface of the insert will be: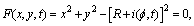
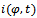 is the linear value of the wear of the insert, and φ is the angle between the radius-vector of any point K of a surface and a vertical axis y.
is the linear value of the wear of the insert, and φ is the angle between the radius-vector of any point K of a surface and a vertical axis y.

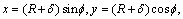
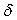 is the displacement of the centre of an axle journal of a shaft.It should be noted that the dimensionless characteristics of the wear process are rather convenient for comparison of wear resistance of self-lubricating materials of SB. The following variable parameters we denote by the following dimensionless symbols:
is the displacement of the centre of an axle journal of a shaft.It should be noted that the dimensionless characteristics of the wear process are rather convenient for comparison of wear resistance of self-lubricating materials of SB. The following variable parameters we denote by the following dimensionless symbols: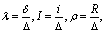
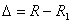 - a radial clearance,
- a radial clearance, 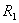 - radius of an axle journal of a shaft.Taking into account (2) and (3), from expression (1) it is found:
- radius of an axle journal of a shaft.Taking into account (2) and (3), from expression (1) it is found: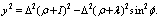
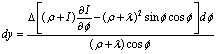
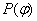 - the contact pressure of the insert acting on a shaft, and τ(φ) is the tangential stresses in the contact surface. Here
- the contact pressure of the insert acting on a shaft, and τ(φ) is the tangential stresses in the contact surface. Here 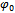 is half of the contact surface angle. We allot the nanoparticle (element K in Fig. 3) of the insert of the SB. In Fig. 3 this element is shown with the forces acting on it. Let’s make a condition of balance of an element K, corresponding to the central angle
is half of the contact surface angle. We allot the nanoparticle (element K in Fig. 3) of the insert of the SB. In Fig. 3 this element is shown with the forces acting on it. Let’s make a condition of balance of an element K, corresponding to the central angle 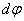 , in the following form:
, in the following form: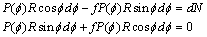
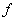 is the coefficient of friction between the axle journal and insert of SB.
is the coefficient of friction between the axle journal and insert of SB.
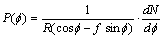
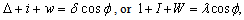
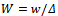 .In work [11] the expression for definition of the elastic displacement of internal surfaces of the insert of SB is deduced, which in our case it becomes:
.In work [11] the expression for definition of the elastic displacement of internal surfaces of the insert of SB is deduced, which in our case it becomes: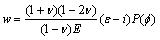
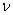 is the coefficient of Poisson, E is the modulus of elasticity, and
is the coefficient of Poisson, E is the modulus of elasticity, and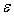 is the thickness of a self-lubricated surface of the insert.Let’s enter a symbol:
is the thickness of a self-lubricated surface of the insert.Let’s enter a symbol: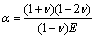
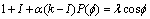
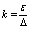 .The boundary conditions of a given task are:
.The boundary conditions of a given task are: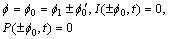
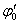 is a contact angle, and
is a contact angle, and  is an angle of displacement of the contact zone with respect to the vertical axis.Substituting the boundary conditions (12) to the equation (11), we receive:
is an angle of displacement of the contact zone with respect to the vertical axis.Substituting the boundary conditions (12) to the equation (11), we receive: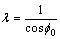
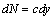
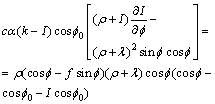
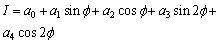
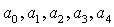 are the unknown factors which are subject to definition.Having substituted expression (16) and its derivative into the equation (15) we receive the following identity:
are the unknown factors which are subject to definition.Having substituted expression (16) and its derivative into the equation (15) we receive the following identity:
 Having equated the coefficients at the
Having equated the coefficients at the 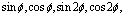 and also a free member we will have the corresponding algebraic equations. After some calculation and simplification these equations will become:
and also a free member we will have the corresponding algebraic equations. After some calculation and simplification these equations will become:
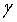 . The velocity of the wear process, taking into account expressions (3) and (16), is defined as:
. The velocity of the wear process, taking into account expressions (3) and (16), is defined as: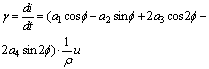
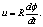 It is necessary to notice that in the SB at the motionless insert and a shaft rotating with constant angular velocity, the velocity of relative sliding of the points of a surface of the insert located in the field of contact will be a constant.One of the important parameters of contact problem of SB is the parameter
It is necessary to notice that in the SB at the motionless insert and a shaft rotating with constant angular velocity, the velocity of relative sliding of the points of a surface of the insert located in the field of contact will be a constant.One of the important parameters of contact problem of SB is the parameter 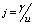 , named the intensity of wear process.From (18) it follows that
, named the intensity of wear process.From (18) it follows that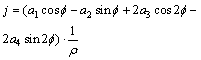
 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-Text HTML
Full-Text HTML