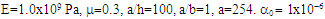Maharudra1, 2, T. Rajanna3, Bheemsha Arya1
1Department of Mechanical Engineering, B.M.S College of Engineering, Bengaluru, Karnataka, India
2Department of Mechanical Engineering, Government Polytechnic College, Bagepalli, Karnataka, India
3Department of Civil Engineering, B.M.S College of Engineering, Bengaluru, Karnataka, India
Correspondence to: Maharudra, Department of Mechanical Engineering, B.M.S College of Engineering, Bengaluru, Karnataka, India.
| Email: |  |
Copyright © 2021 The Author(s). Published by Scientific & Academic Publishing.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/

Abstract
The study presents the effect of uniformly distributed various thermal loads on the thermal buckling characteristics of trapezoidal laminates by developing finite element formulation. Towards this, the trapezoidal panel is discretised by using a 9-noded heterosis plate element by incorporating the effect of shear deformations and rotary inertia. The effectiveness off the presents formulation is verified by correlating present findings with the accessible literature. The present study involves the effect of various parameters like the intensity of temperature, trapezoidal shape, ply-orientation, panel edge conditions, panel width to thickness ratio etc. It is observed from the study that the trapezoidal shape and its boundary conditions significantly affect the thermal bucking characteristics of thin panels.
Keywords:
Trapezoidal shape, Thermal buckling, Laminated composites, Thermal Load, Heterosis element
Cite this paper: Maharudra, T. Rajanna, Bheemsha Arya, Thermal Buckling Behaviours of Laminated Composite Trapezoidal Panel under Thermally Induced Loads, American Journal of Materials Science, Vol. 11 No. 1, 2021, pp. 10-19. doi: 10.5923/j.materials.20211101.02.
1. Introduction
Advances in material science have resulted in a remarkable rise in the allowable material stress level. Laminated composites is often employed to replaces traditional metal for the skin panels of aircraft wings and fuselages in order to reduces the weights of aerospace vehicles. In the designs of composites skins for aircraft wings, one of the important issues is thermals buckling of the panels. High-speed aircraft structural panels are subjected not only to aerodynamics loading, but also to aerodynamics heating. The laminated composites structures are very much vulnerable to elevated heats or temperatures and which leads to considerable degradation of strengths and other damaging effects. In practices, the laminated composites panels are not always rectangular or square in shape, but which are of different shapes. For instance, the aircraft wings and ship bodies are made up of trapezium panels which are located at some regions. Most of the literature covers the stability analysis of rectangular and square panels under thermal loads, but trapezoidal plates are also commonly founds. And there is not enough literature regarding these trapezoidal plates. The in-plane thermal stresss distributions within such panels is not uniform, the existence of stresses may also be vary in different regions, resulting in loss of stability at an extremely low levels of stress. Therefore, the complete knowledge of thermal buckling behaviour of trapezoidal panels is most necessary in order to prevent the premature failures and to use their full strengths. This can be explored to a great extent in the area of thin walled structures. Ganapathi et al. (2018) and Biswal et al. (2016) studied the effects of hygrothermal loading on the buckling behaviour of laminated composites plates by adopting the finite elements techniques (FE). This study is restricted to the square/rectangular plates and a quadratic iso-parametric eight-noded elements with first-order shear deformation theory (FSDT) has been used in their study. However, for certain mesh configurations and boundary conditions, the eight-noded plate elements appears to be locks in shear, even when selective or reduced integration techniques are used for a thin plates configurations. It is also stated that the eight-node serendipity elements is comparatively more sensitive to elements aspects ratios and elements shape distortions Rajanna et al. (2016). Rath and Sahu (2013) adopted the finite elements modelings approach for investigating the parametric instability of laminated panels subjected to periodic dynamic loading in hygro-thermal environment. Theoretical and analytical investigations based on the finite elements methods were performed by Panda et al. (2013) to study hygro-thermal effectss on free vibrations of delaminated woven composites fibres panels. On the vibrations actions of woven fibre glass/epoxy delaminated composites panels subjected to elevated temperatures and humidity were studied by Parhi et al. (2013). The thermals bucklings behaviours of shear deformable functionally graded single/doubly curved shell panels with temperature dependent (TD) and temperature independent (TID) properties were studied by Vishesh et al. (2016). Using the finites elements methods (FEM) via a 3D eight-noded solid element, Na and Kim (2004) investigated the thermals bucklings behaviours of the FG (fractionally graded) panel. Abdelhak et al. (2015) examined FGM (functionally graded material) panels thermals buckling behaviour using four variables theory in the nth order. Hygro-thermal effects on the bendings of angle-ply composites panels were examined by Zenkour (2012) using a sinusoidal theory. To present hygro-thermal effects on the stretching behaviour of laminated composites panels, Ram and Sinha (1991) have been used the finite elements methods. The effects of hygro-thermal environments on post buckling behaviour of laminated panels has been studied by Shen et al. (2001). The hygro-mechanical connections and multiscales swellings coefficients evaluations of flax yarns and flax/epoxy composites have recently had been investigated by Marwa et al. (2020). Abdelmalek et al. (2017) observed the hygro-thermal effects of composites panels free vibrations behaviour using node n-order shear deformation theory. The research of hygro-thermal effects on stress analysis of tapered laminated composites beam were conducted by Debabrata et al. (2013). Madhusmita et al. (2016) investigated the impacts of hygro-thermal effects on the buckling behaviour of laminated composites cylindrical shell panels. Patel et al. (2002) used higher-order theory to do his research on hygro-thermal effects on the structurals behaviour of thick composites laminates. The effects of thermals buckling behaviour of hybrid angle-ply laminated composite panels with a hole was studied by Sinan (2005). Abdelbaki et al. (2017) did their research on thermals buckling using a simplified higher orders shear deformation theory (HSDT) for cross-ply laminated panels. Chandrashekhara (1992) have been investigated the thermals buckling behaviours of laminated panels using a shear flexible finite element.From the above literature study, it may be concluded that vast amount of literature are available, which deals with the buckling behaviour of laminated panels subjected to hygro-thermal loads, but they are restricted to rectangular or square shaped panels. No work is found in the literature, as per the knowledge of the authors, which relates to the effect of temperatures on the trapezoidal laminate panel under thermal buckling behaviour. Therefore, by conspiring various parameters such as trapezoidal shape, ply-orientation, panel edge conditions, width to thickness ratio etc. Through this work, an effort is made to study the impact of trapezoidal shape and other parameters on the buckling behaviour of panel under different elevated temperature by adopting 9-noded heterosis plate elements. This kind of element exhibits higher accuracy as compared to that of 8–noded serendipity and 9-noded lagrangian elements even at extremely thin plate configurations.
2. Mathematical Formulation
The basic form of the problem considered here is a trapezoidal shaped panel, whose geometry and meshing pattern considered are shown in Figs 1(a) and 1(b) respectively.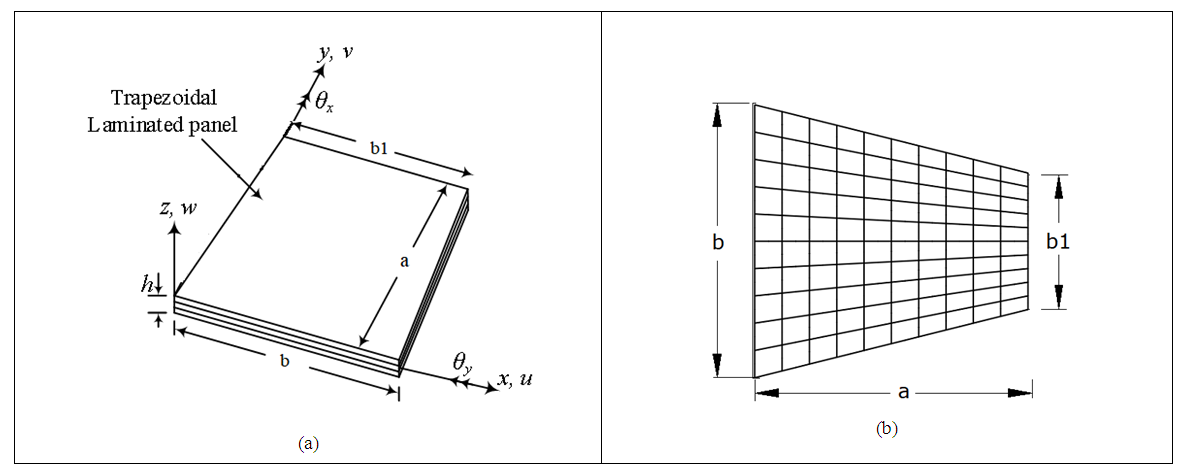 | Figure 1. (a) Geometry of the panel with its co-ordinate system. (b) Panel with a meshing type |
The panel is assumed to consist of N orthotropic layers. Each layer has arbitrary fiber orientation. The displacement field may be expressed as (Subash et al. 2020)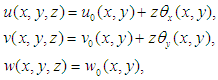 | (1) |
where u0 and v0 are the mid-plane in-plane displacement components of the panel; θx and θy are rotations of the mid-plane with respect to y and x axes respectively; w0 is the out-of-plane displacement component of the panel. The kinematic relation can be determined as,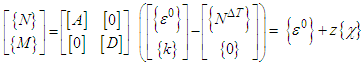 | (2) |
The stress-strain relation for a lamina with reference to the plate axes is given by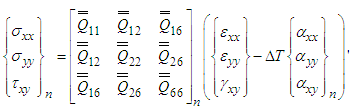 | (3) |
where 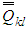 are the transformed reduced stiffness,
are the transformed reduced stiffness, 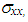
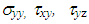 and
and 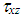 are the stress components,
are the stress components, 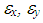 and
and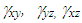 denotes the bending strains and shear strains respectively at any point on the laminated plate and
denotes the bending strains and shear strains respectively at any point on the laminated plate and 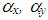 are the thermal expansion coefficients in x and y direction, respectively.
are the thermal expansion coefficients in x and y direction, respectively. 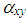 is the coefficient of thermal in shear.By using Eqns (1) and (3), the constitutive relation for the symmetric laminated panel can be given by
is the coefficient of thermal in shear.By using Eqns (1) and (3), the constitutive relation for the symmetric laminated panel can be given by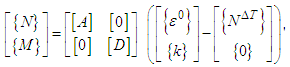 | (4) |
where [A] and [D] are the extensional rigidity and bending rigidity of the panel, respectively. The thermal forces 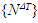 induced by the temperature change are defined as
induced by the temperature change are defined as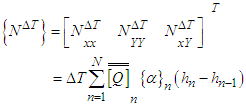 | (5) |
The total strain energy for the thermals buckling of composite laminated panel can be expressed as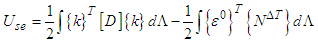 | (6) |
By following the procedure described in the strain energy of a quadratic element can be expressed as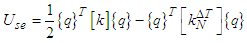 | (7) |
where 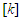 and
and 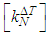 are the elements bending stiffness matrix, geometrical stiffness matrix due to thermal effect and {q} contains the nodal degree of freedom.The boundary conditions for simply supported and clamped supported edges can be described as (Muddappa et al. 2021),(1) Simply supported condition (SSSS):At x = 0, a; u0 = w0= θy = 0At y = 0, b; v0 = w0 = θx = 0(2) Clamped condition (CCCC):At x =0, a; u0 = v0 = w0 = θx = θy = 0At y =0, b; u0 = v0 = w0 = θx = θy = 0After assembling the element matrices and vectors and then applying suitable boundary conditions, the governing equation in matrix form for the thermal buckling analysis of the composite laminated panel is obtained as
are the elements bending stiffness matrix, geometrical stiffness matrix due to thermal effect and {q} contains the nodal degree of freedom.The boundary conditions for simply supported and clamped supported edges can be described as (Muddappa et al. 2021),(1) Simply supported condition (SSSS):At x = 0, a; u0 = w0= θy = 0At y = 0, b; v0 = w0 = θx = 0(2) Clamped condition (CCCC):At x =0, a; u0 = v0 = w0 = θx = θy = 0At y =0, b; u0 = v0 = w0 = θx = θy = 0After assembling the element matrices and vectors and then applying suitable boundary conditions, the governing equation in matrix form for the thermal buckling analysis of the composite laminated panel is obtained as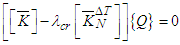 | (8) |
The thermal buckling analysis has been represented as the standard eigenvalue problem. The critical buckling temperature 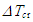 may be found from the eigenvalue
may be found from the eigenvalue  which is equal to
which is equal to 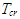 .
.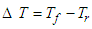 | (9) |
where, ∆T is the temperature difference between the final temperature (Tf )and the reference temperature (Tr).
2.1. Finite Element Formulation
A computer program by using FORTRAN language has been developed to work out buckling problems. The different participating matrices are acquired by assembling each individual element level matrices which are retained in a skyline technique. Eigenvalues and eigen-vectors involved are extracted by using subspace iterations technique. In the computer program, a selective integration scheme, in which 3 x 3 Gauss rule for membranes as well as deflection terms and 2 x 2 Gauss rule for shear terms has been incorporated to generate element elastic stiffness matrix without any shear locking. Similarly, full integration scheme (i.e., 3 x 3 Gauss rule) has been used for both geometric stiffness as well as mass matrices. Figure 2 shows the schematic examples of various this types of elements.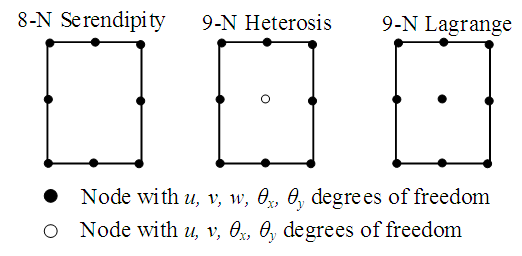 | Figure 2. Schematic example of various types of elements |
9-noded heterosis panel element has been employed in the current research to study the thermal buckling behaviour of the trapezoidal panel. By use of minimum potential energy rule, the stiffness matrix of the panel is achieved. Bending stiffness [Kbs], shear stiffness [Kss] and geometric stiffness [Kgs] can be represented as: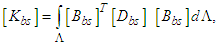 | (8) |
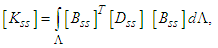 | (9) |
and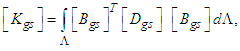 | (10) |
Where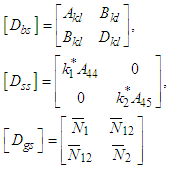 | (11) |
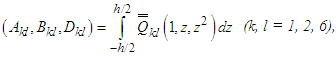 | (12) |
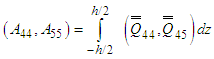 | (13) |
Here 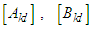 and
and 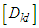 represents extensions, extensions-bending and bending stiffness respectively. Compared to A44 and A55, in which the terms A45 is ignored and the shear corrections factors for the trapezoidal cross-sections are donated by
represents extensions, extensions-bending and bending stiffness respectively. Compared to A44 and A55, in which the terms A45 is ignored and the shear corrections factors for the trapezoidal cross-sections are donated by 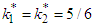 . The overall matrices are receives by assembling the corresponding elements stiffness, geometric stiffness matrices using the skyline technique.
. The overall matrices are receives by assembling the corresponding elements stiffness, geometric stiffness matrices using the skyline technique.
3. Results and Discussions
There are several methods to solving eigenvalue problem. In this analysis, the subspace iteration technique is adopted to get numerical solutions to the problems in order to obtain the eigenvalues. The angle-ply and cross-ply laminated trapezoidal composite panels used here have multiples thicknesses and are symmetrically bonded.The trapezoidal laminated panel considered in this research is a thin panel with h/b = 0.01 and having 4 layers, each layer is having the equal thickness of 0.5mm unless otherwise stated, the thermo-elastic properties of the material that are used for E-glass/epoxy are shown in Table 1.Table 1. Material properties used for numerical solutions at different temperature (Sai ram 1991)
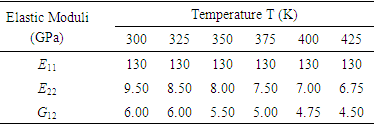 |
| |
|
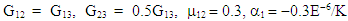 and
and 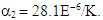 Here
Here 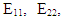 and
and 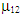 are modulus of elasticity in direction 1 and 2 and Poison’s ratio, respectively.
are modulus of elasticity in direction 1 and 2 and Poison’s ratio, respectively.  are the coefficients of thermal expansion of the materials considered in the solution.
are the coefficients of thermal expansion of the materials considered in the solution.
3.1. Comparison and Convergence Study
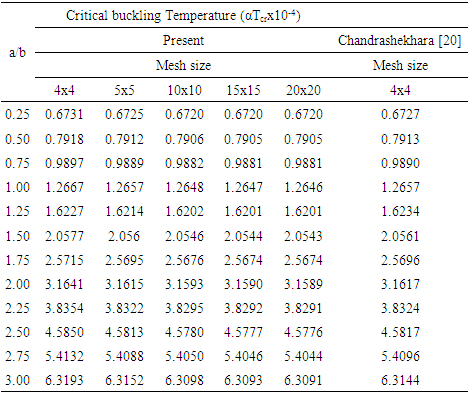
Table 2. Comparison of non-dimensional buckling temperature under simply supported boundary condition for isotropic thin panel
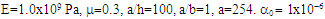
 |
| |
|
In order to test the validity of the mesh to be considered for relatively accurate converged outcomes, the convergence study is most important. A 10 x 10 mesh size is found to be so well converged in this study and throughout this work the same mesh sizes is chosen as observed in Table 2. The graphical representation of convergence study can also be seen in Fig. 3. On the other hand, the comparison study is also most pertinent to determine the accuracy of the convergence study established for thermal buckling of laminated panel to validate the current finite element software. The comparisons of the current results gathered against the existing results are shown in Table 2 along with the results of (Chandrashekhara 1992). The present results are well agreed with the literature.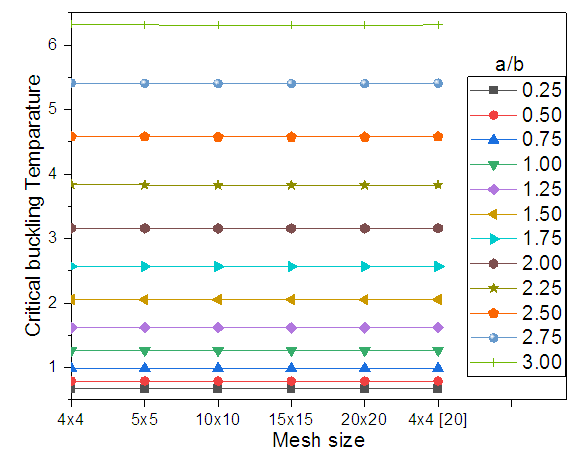 | Figure 3. Convergence behaviour of thermal buckling with different a/b ratios |
3.2. Case studies on the Buckling Behaviour of Trapezoidal Panel Under Uniform Thermal Loads
In this sections, the thermals buckling behaviour of angle-ply and cross-ply trapezoidal laminated panels are examined by considering various temperatures, width to thickness ratio and different trapezoidal shapes, etc. The term trapezoidal shape indicates when the percentage of b1/b value changes from 0.5 to 1 and when b1 equal to 1 indicates the square panel. Set of six different temperatures have been considered to study the thermal buckling behaviour of composites panel and the performance of each parametric condition is investigated in detail in the following sub-sections.
3.2.1. Effect of Ply-Orientations and Temperatures on the Thermal Buckling Behaviour
The thermal buckling behaviour of trapezoidal panels with trapezoidal shape ratio (b1/b) 0.9 is considered here. The effect of various temperature and the ply-orientations are deliberated in this section and the results are illustrated in Figs 4 and 5 by considering simply supported (SSSS) and clamped (CCCC) boundary conditions respectively. It is evident from Figs 4 (a) and 4 (b) that the thermals buckling load (Tcr) increases with the increases in ply-angle and found to be the highest at a ply-orientations of (±45)s thereafter reduces with the further increase in ply-angle. It is necessary to be noted that the value of Tcr is significantly higher when for b/h = 5 as compared to that of b/h = 100. When b/h = 5, this means that the thick panel. This may be due to the effect of high stiffness of the material. The critical buckling temperature reduces significantly as the b/h ratio increases. It is also important to remember that the critical thermal buckling (Tcr) increases with decrease in temperature, and is found to be the highest at a temperature of 325 K. This difference is much more significant as compared with the temperature of 425 K. It is worthwhile to mention that, thick laminated panel with lower temperature show higher buckling resistance. Moreover the clamped edged boundary condition will always shows the highest thermal buckling resistance as compared with the simply supported edge condition in both thick and thin laminates as shown in Figs 5 (a) and 5 (b) respectively.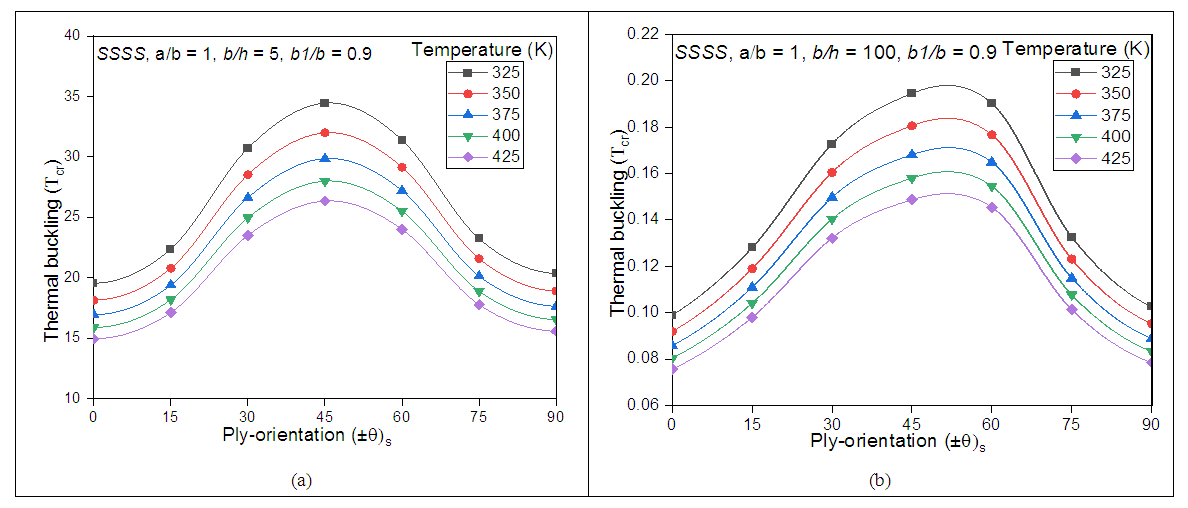 | Figure 4. Thermal buckling behaviour under 4ply-orientations by considering SSSS edged (a) thick and (b) thin laminates |
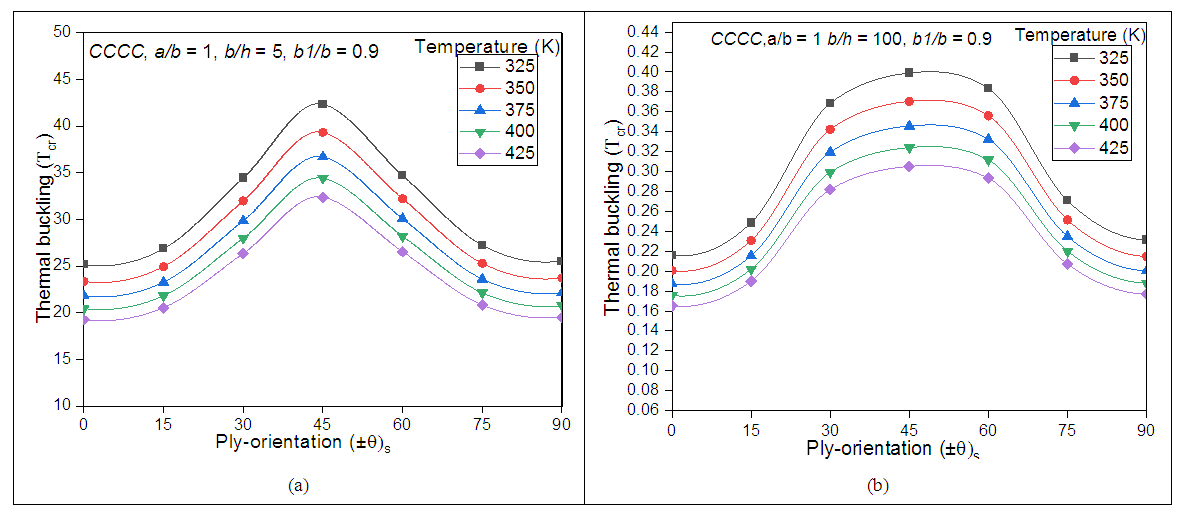 | Figure 5. Thermal buckling behaviour under ply-orientations by considering CCCC edged (a) thick and (b) thin laminates |
3.2.2. Effect of Trapezoidal Shapes and Temperature on Thermal Buckling Behaviour
The effect of different trapezoidal shapes and the various temperatures on the thermal buckling behaviour of composite laminates are observed in this section and the results are illustrated in Figs 6 (a) and 6 (b) by considering cross-ply and angle-ply laminate schemes respectively. Clamped edge condition with b/h = 50 are considered to know the effect of thermal buckling behaviour of the trapezoidal panel with b1/b = 0.9. From the Figs 6 (a) and 6 (b), it is clear that the thermal buckling resistivity of the panel progressively decreases as the temperature increases. However, angle-ply composite laminates is having the highest thermal buckling resistance, when compared with a cross-ply laminates at the same temperatures conditions. However, it is observed much variation in the thermal buckling, as the trapezoidal shape increases. It is also observed that, as the trapezoidal shape ratio increases, the thermal buckling increases and is found to be maximum at b1/b = 0.5. This increasing buckling strength may be due to the increase in stiffness of the panel due to the reduction of span length. However, the thermal buckling resistance of the trapezoidal panel is minimum, when the b1/b = 1.0 i.e square laminated panel.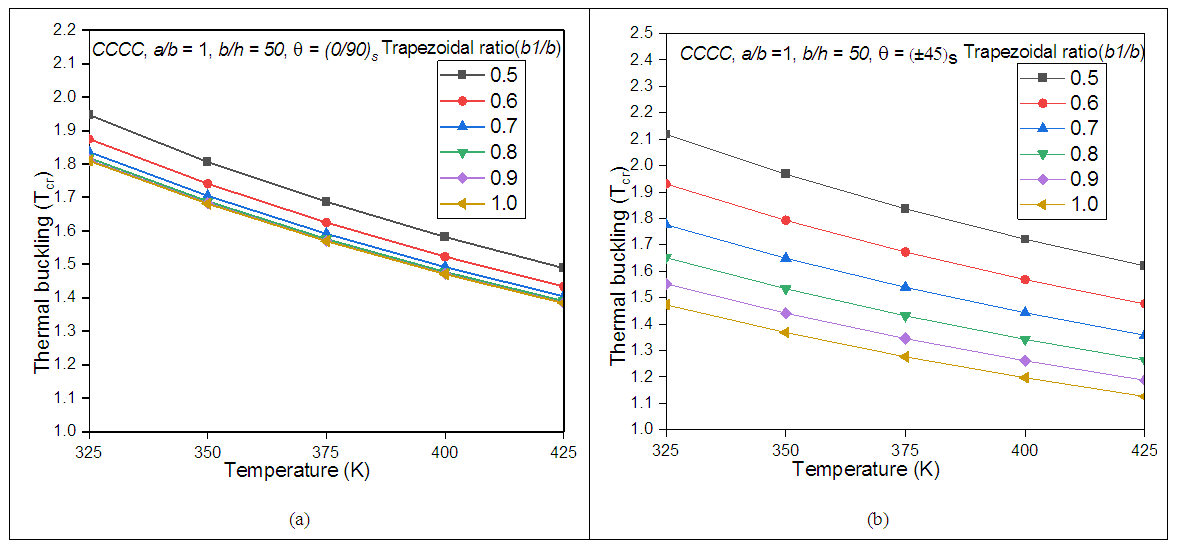 | Figure 6. Thermal buckling behaviour of different trapezoidal shapes (a) cross-ply and (b) angle-ply laminates |
3.2.3. Effect of Plate Aspect Ratio and the Temperatures on the Thermal Buckling Behaviour
Effect of different plate aspect ratios and the temperatures on the thermal buckling behaviour of the trapezoidal panel have been investigated in this section and the results are illustrated in Figs 7 and 8 by considering simply supported and clamped boundary conditions respectively. The trapezoidal shape which is considered here is having the trapezoidal shape ratio (b1/b) = 0.9. Both simply supported and the clamped boundary edges are considered with the cross-ply and angle-ply laminate schemes. It is observed from the study that as the plate aspect ratio increases, the thermal buckling decrease and found to be maximum when the a/b = 1. It is also observed from the study that, as the temperature increases, the thermal buckling reduces and found to be minimum where the temperature is 425 K. However, the thermal buckling resistance is quite higher in case of clamped edge restriction as compared with the simply supported edge restriction as shown in figures 8 (a) and 8 (b). Moreover angle-ply scheme shows the higher critical thermal buckling resistivity as compared with the cross ply scheme at simply supported boundary condition. It is also noting from Figs 8 (a) and 8 (b) that, the thermal buckling is found to be maximum in case of cross-ply composite laminates at clamped boundary conditions. It is evident from Figs 7 (a) to 8 (b) that the thermal buckling resistance of panel reduces with the increase in uniform temperature load. 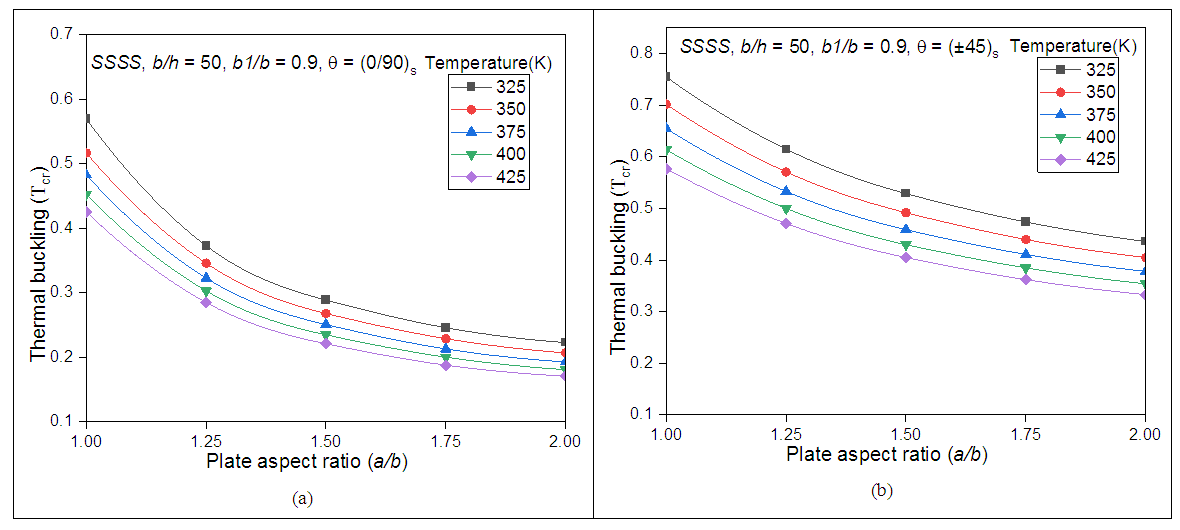 | Figure 7. Thermal buckling behaviour under different width ratios of SSSS edged (a) cross-ply and (b) angle-ply laminates |
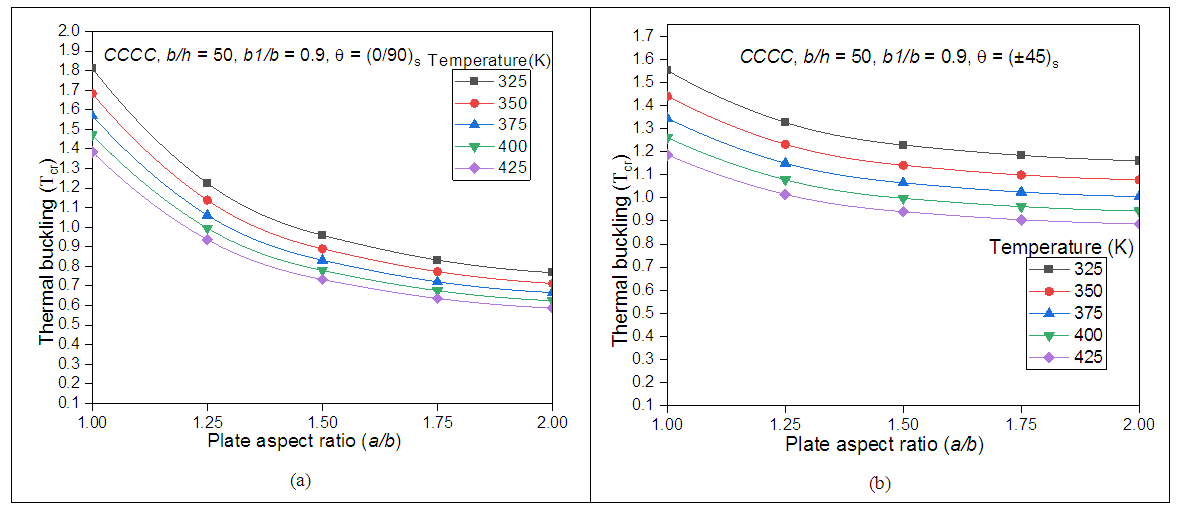 | Figure 8. Thermal buckling behaviour under different width ratios of (a) cross-ply and (b) angle-ply laminates |
3.2.4. Effect of Different Thickness and Temperatures on the Thermal Buckling Behaviour
A similar research is carried out to examine the effect of panel thickness and the temperatures on the thermal buckling behaviour of the trapezoidal panel. By taking angle-ply and cross-ply configurations with all four edges are clamped supported, the effect of thickness are exemplified in Figs 9 (a) and 9 (b) respectively. The Trapezoidal shape which is considered here is having the trapezoidal shape ratio (b1/b) is 0.9. The b/h ratios considered here are 10, 20, 30, 40 and 50, which represents thick to thin in nature. It is very clear from Figs 9 (a) and 9 (b) that the value of Tcr is reduces with the increase in panel thickness ratio with respective to a temperature loading. The highest thermal buckling is found in case of cross ply laminates i.e (0/90)s. As the thickness and the temperature further increases, there is not much of the increase in the thermal buckling stability found, wherein the amount of Tcr found to be remain unchanged for thin laminated panels. However, there is much variation in the thermal buckling resistance in the case of thick laminates. It may be due to the good strength and stiffness of the thick composite laminated panel.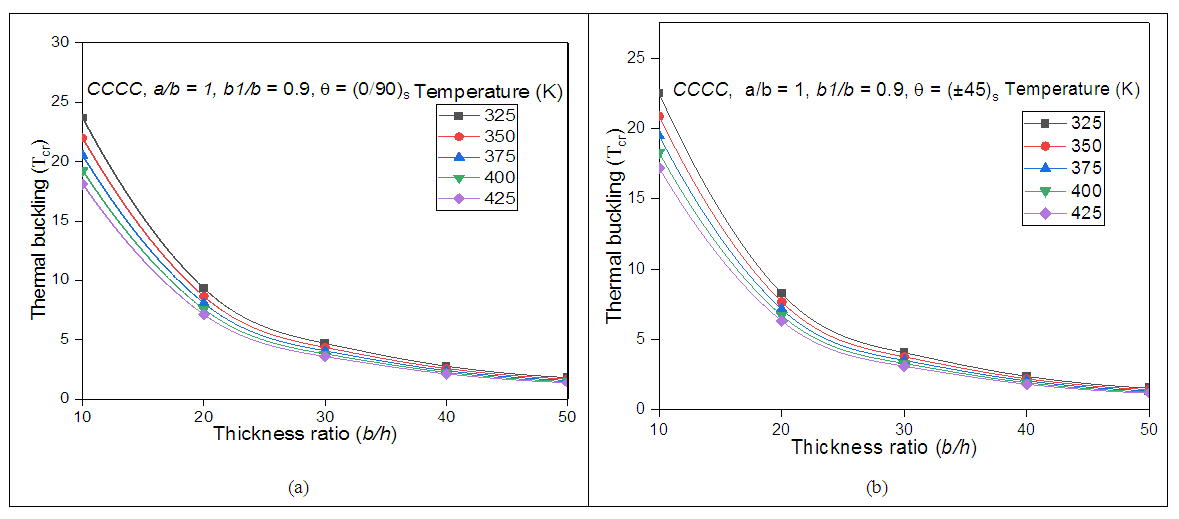 | Figure 9. Thermal buckling behaviour under different thickness by considering (a) cross-ply and (b) angle-ply laminates |
An impact of various temperatures and the thickness on the non-dimensional stability resistance of simply supported (SSSS) and clamped (CCCC) conditions of trapezoidal panel have been investigated in this section by considering angle-ply layup scheme and the numerical results are shown in Figs 10 (a) and 10 (b) respectively. The trapezoidal panel considered in this investigation is subjected to uniform thermal load with various thickness ratios (b/h) and trapezoidal shape ratio (b1/b) = 0.9. It is inferred from Figs 10 (a) and 10 (b) that, as the temperature increases, the thermal buckling resistance reduces. However, as the b/h ratio of the composite laminate increases, the laminated panel becomes thinner in nature and hence reduction in the thermal buckling resistance. It is clear from the study that, the CCCC boundary condition has a higher buckling resistance as compared with SSSS boundary condition at different temperatures as well as thicknesses. It should be noted that, only in thin panel the impact of CCCC and SSSS boundary conditions play an important role in the non-dimensional buckling resistance of the trapezoidal shaped panel.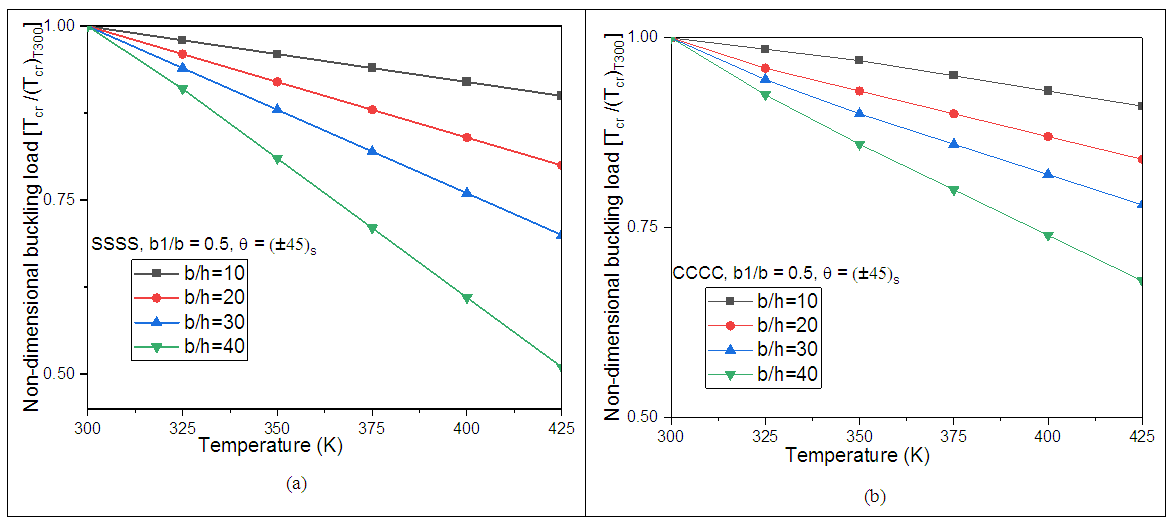 | Figure 10. Non-dimensional buckling behaviour under different thickness by considering (a) SSSS and (b) CCCC boundaries |
3.2.5. Impact of Different Boundary Conditions on the Thermal Buckling Behaviour
An impact of various boundary conditions and different temperatures are considered to know the thermal buckling behaviour of trapezoidal panel in this section. A variation in the thermal buckling behaviour under different boundary conditions is shown in the Figs 11 (a) and 11 (b) by considering cross-ply and angle-ply laminate schemes respectively. It is observed from Figs 11 (a) and 11 (b) that the buckling resistance of trapezoidal panel reduces with the increase in temperature with various boundary conditions and is maximum at CCFF edge condition in the case of cross-ply trapezoidal composite laminated panel, whereas the thermal buckling resistance is found maximum at CCCC boundary condition in the case of angle-ply trapezoidal composite laminated panel at the same thickness. It is also observed that, minimum thermal buckling resistance found at SSSS and SSFF boundary condition at cross-ply and angle-ply respectively.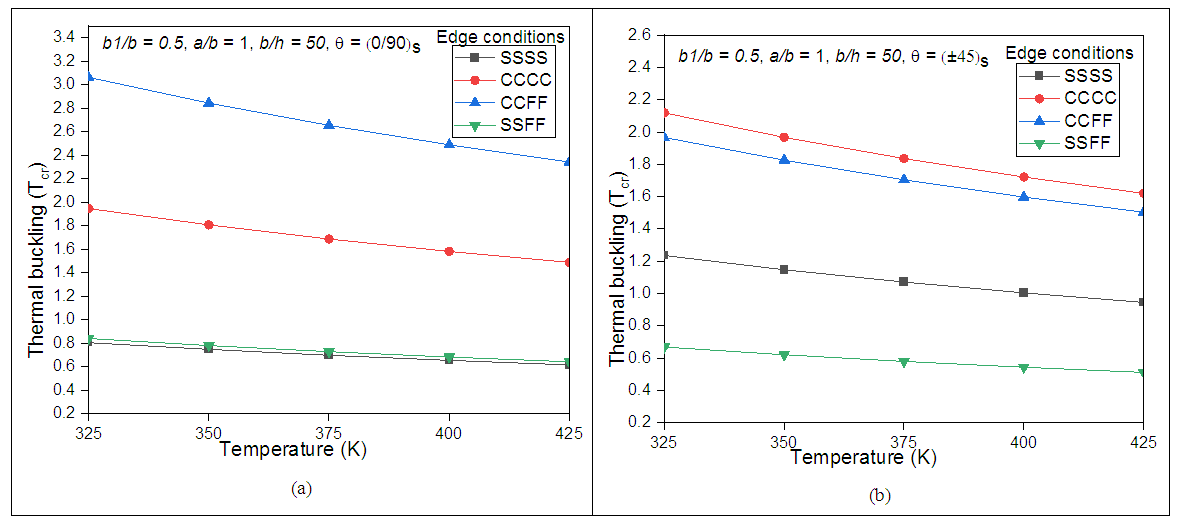 | Figure 11. Thermal buckling behaviour under different boundary conditions of ( a) cross-ply and (b) angle-ply laminates |
4. Conclusions
Thermal buckling behaviour of trapezoidal laminated panel has been studied by considering various temperatures, thickness, aspect ratio and boundary conditions in both cross-ply and angle-ply laminate schemes. A nine-node heterosis plate element has been employed in the current research to study the thermal buckling analysis of composite laminated trapezoidal panels. Based on the present results, the following conclusions can be drawn.Ø The trapezoidal shape ratios (b1/b) play a significant role in the thermal buckling resistance. For a given parameter, the thermal buckling resistance increases with the increase in b1/b ratio and found to be higher at b1/b = 0.5. Ø The ply-orientation also play a significant role in the thermal buckling resistance, wherein the thermal buckling resistance of the panel increases with the increase in ply-orientation and found to be highest at an angle of (±45)s. Ø As the thickness ratio increases, the laminated panel becomes thinner in nature. This will reduces the stiffness of the laminated panel resulting reduction in the thermal buckling resistance. It is observed that, as the b/h ratio increases, the thermal buckling resistance decreases and is found to be lowest at b/h = 100.Ø It is also observed from the study that, for any given boundary condition, the value of Tcr is initially higher at a temperature of 325 K and gradually reduces as the temperature increases uniformly.Ø The panel with CCFF edge condition shows highest critical buckling temperature in the case of cross-ply scheme, whereas it is CCCC edge conditions in the case of angle-ply scheme.Ø The thermal buckling variation among different temperature is found to be significant in the case of thicker panel, i.e., for lower b/h ratio and this variation keep on reduces and becomes insignificant in the case of thin panels. Ø For a given temperature, the thermal buckling variation among different trapezoidal ratio (b1/b) shows significantly higher in the case of angle-ply scheme as compared to that of cross-ply laminate scheme. Ø For any selected parameter, the thermal buckling resistance of the panel decreases with the increase in the plate aspect ratios.
References
| [1] | G. Manickam, A. Bharath, A.N. Das, A. Chandra and P. Barua, Thermal buckling behaviour of variable stiffness laminated composite plates, Materials Today Communications 16 (2018) 142-151. |
| [2] | M. Biswal, S. Sahu, A. Asha, “Vibration of composite cylindrical shallow shells subjected to hygrothermal loading-experimental and numerical results,” Composites Part B: Engineering 98 (2016) 108-119. |
| [3] | T. Rajanna, Sauvik Banerjee, Yogesh M. Desai, D. L. Prabhakara. Effects of Partial Edge Loading and Fibre Configuration on Vibration and Buckling Characteristics of Stiffened composite plates. Latin American Journal of Solids and Structures 13 (2016) 854-879. |
| [4] | M.K. Rath, S.K. Sahu, “Parametric Instability of Square Laminated Panels in Hygrothermal Environment,” Journal of Structures (2013). |
| [5] | H. Panda, S. Sahu, P. Parhi, “Hygrothermal effects on free vibration of delaminated woven fiber composite panels– Numerical and experimental results,” Composite Structures 96 (2013) 502-513. |
| [6] | Vishesh R. Kar, Subrata K. Panda and Trupti R. Mahapatra, “Thermal buckling behaviour of shear deformable functionally graded single/doubly curved shell panel with TD and TID properties,” Advances in Materials Research 5 (4) (2016) 205-221. |
| [7] | Na, K.S. and Kim, J.H, “Three-dimensional thermal buckling analysis of functionally graded materials,” Compos. Part B-Eng. 35 (5) (2004) 429-437. |
| [8] | Abdelhak, Z., Hadji, L., Daouadji, T.H. and Bedia, E.A., “Thermal buckling of functionally graded panels using a n-order four variable refined theory,” Adv. Mat. Res. 4 (1) (2015) 31-44. |
| [9] | Ashraf M. Zenkour,”Hygrothermal effects on the bending of angle-ply composite panels using a sinusoidal theory,” Composite Structures 94 (2012) 3685–3696. |
| [10] | K. S. Sai Ram and P. K. Sinha, “Hygrothermal effects on the bending characteristics of laminated composite panel”, Int. Journal of computers and structures 40 (4) (1991) 1009–1015. |
| [11] | Shen H. S. “Hygrothermal effects on the postbuckling of shear deformable laminated panels,” Int J Mech Sci 43(2001) 1259–81. |
| [12] | Marwa Abidaa, Florian Gehringa, Jamel Marsb, Alexandre Viveta, Fakhreddine Dammakb, Mohamed Haddarc, “Hygro-mechanical coupling and multiscale swelling coefficients assessment of flax yarns and flax / epoxy composites”, Composites Part A 136 (2020) 105914. |
| [13] | Abdelmalek Abdelmalek, Mokhtar Bouazza, Mohamed Zidour, Noureddine Benseddiq, “Hygrothermal Effects on the Free Vibration Behaviour of Composite Panel Using nth-Order Shear Deformation Theory: a Micromechanical Approach,” Iran J Sci Technol Trans Mech Eng (2017). |
| [14] | Debabrata Gayen, Tarapada Roy, “Hygro-Thermal Effects on Stress Analysis of Tapered Laminated Composite Beam,” International Journal of Composite Materials 3 (3) (2013) 46-55. |
| [15] | Madhusmita Biswal, Shishir Kr. Sahu, A.V. Asha and Namita Nanda, “Hygrothermal effects on buckling of composite shell-experimental and FEM results,” Steel and Composite Structures 22 (6) (2016) 1445-1463. |
| [16] | B. P. Patel, M. Ganapathi, D.P. Makhecha, “Hygrothermal effffects on the structural behaviour of thick composite laminates using higher-order theory,” Composite Structures 56 (2002) 25–34. |
| [17] | Omer Sinan Sahin, “Thermal buckling of hybrid angle-ply laminated composite panels with a hole,” Composites Science and Technology 65 (2005) 1780–1790. |
| [18] | Abdelbaki Chikh, Abdelouahed Tounsi, Habib Hebali and S. R. Mahmoud, “Thermal buckling analysis of cross-ply laminated panels using a simplified HSDT,” Smart Structures and Systems 19 (3) (2017) 289-297. |
| [19] | Bathe, Klaus-Jürgen. 2014. “Finit Elements Procedures. Second Edi,” Prentice Hall, Pearson Education, In. |
| [20] | K. Chandrashekhara, “Thermal buckling of laminated panel using a shear flexible finite element,” Finite Elements in Analysis and Design 12(1992) 51-61. |
| [21] | Maharudra, B. Arya, T. Rajanna, “Effect of ply-orientation and boundary conditions on the vibrational characteristics of laminated composite panels using HOSDT,” Mater. Today: Proc. 20 (2020) 134–139. |
| [22] | K.S. Subash Chandra, T. Rajanna, and K. Venkata Rao, “A Parametric study on the effect of elliptical cutouts for buckling behaviour of composite plates under non-uniform edge loads,” Latin American Journal of Solids and Structures 17 (2020) 1-15. |
| [23] | P.P. Yathish Muddappa, T. Rajanna, G. Giridhara. “Effects of different interlaminar hybridization and localized edge loads on the vibration and buckling behaviour of fiber metal composite laminates,” Composites Part C 4 (2021) 100084. |



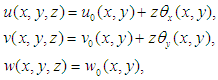
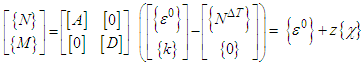
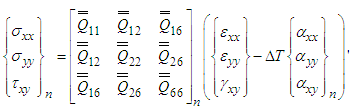
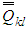 are the transformed reduced stiffness,
are the transformed reduced stiffness, 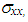
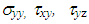 and
and 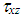 are the stress components,
are the stress components, 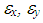 and
and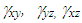 denotes the bending strains and shear strains respectively at any point on the laminated plate and
denotes the bending strains and shear strains respectively at any point on the laminated plate and 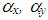 are the thermal expansion coefficients in x and y direction, respectively.
are the thermal expansion coefficients in x and y direction, respectively. 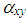 is the coefficient of thermal in shear.By using Eqns (1) and (3), the constitutive relation for the symmetric laminated panel can be given by
is the coefficient of thermal in shear.By using Eqns (1) and (3), the constitutive relation for the symmetric laminated panel can be given by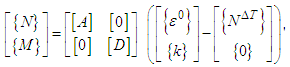
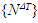 induced by the temperature change are defined as
induced by the temperature change are defined as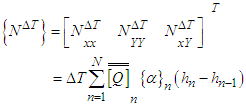
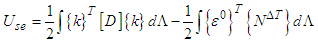
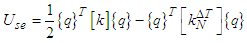
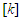 and
and 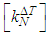 are the elements bending stiffness matrix, geometrical stiffness matrix due to thermal effect and {q} contains the nodal degree of freedom.The boundary conditions for simply supported and clamped supported edges can be described as (Muddappa et al. 2021),(1) Simply supported condition (SSSS):At x = 0, a; u0 = w0= θy = 0At y = 0, b; v0 = w0 = θx = 0(2) Clamped condition (CCCC):At x =0, a; u0 = v0 = w0 = θx = θy = 0At y =0, b; u0 = v0 = w0 = θx = θy = 0After assembling the element matrices and vectors and then applying suitable boundary conditions, the governing equation in matrix form for the thermal buckling analysis of the composite laminated panel is obtained as
are the elements bending stiffness matrix, geometrical stiffness matrix due to thermal effect and {q} contains the nodal degree of freedom.The boundary conditions for simply supported and clamped supported edges can be described as (Muddappa et al. 2021),(1) Simply supported condition (SSSS):At x = 0, a; u0 = w0= θy = 0At y = 0, b; v0 = w0 = θx = 0(2) Clamped condition (CCCC):At x =0, a; u0 = v0 = w0 = θx = θy = 0At y =0, b; u0 = v0 = w0 = θx = θy = 0After assembling the element matrices and vectors and then applying suitable boundary conditions, the governing equation in matrix form for the thermal buckling analysis of the composite laminated panel is obtained as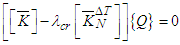
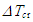 may be found from the eigenvalue
may be found from the eigenvalue 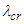 which is equal to
which is equal to 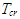 .
.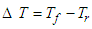

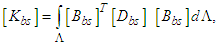
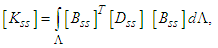
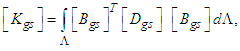
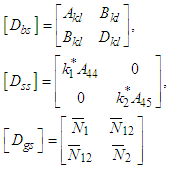
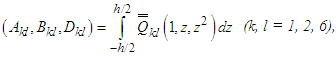
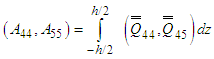
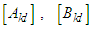 and
and 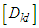 represents extensions, extensions-bending and bending stiffness respectively. Compared to A44 and A55, in which the terms A45 is ignored and the shear corrections factors for the trapezoidal cross-sections are donated by
represents extensions, extensions-bending and bending stiffness respectively. Compared to A44 and A55, in which the terms A45 is ignored and the shear corrections factors for the trapezoidal cross-sections are donated by 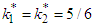 . The overall matrices are receives by assembling the corresponding elements stiffness, geometric stiffness matrices using the skyline technique.
. The overall matrices are receives by assembling the corresponding elements stiffness, geometric stiffness matrices using the skyline technique.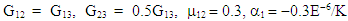 and
and 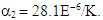 Here
Here 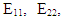 and
and 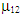 are modulus of elasticity in direction 1 and 2 and Poison’s ratio, respectively.
are modulus of elasticity in direction 1 and 2 and Poison’s ratio, respectively. 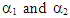 are the coefficients of thermal expansion of the materials considered in the solution.
are the coefficients of thermal expansion of the materials considered in the solution.








 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML