-
Paper Information
- Next Paper
- Previous Paper
- Paper Submission
-
Journal Information
- About This Journal
- Editorial Board
- Current Issue
- Archive
- Author Guidelines
- Contact Us
American Journal of Materials Science
p-ISSN: 2162-9382 e-ISSN: 2162-8424
2015; 5(2): 41-46
doi:10.5923/j.materials.20150502.03
Effect of Low Gamma-Irradiation Doses on Cellulose Triacetate Polymer Films: I. Dispersion Properties
M. S. Abd El Keriem
Physics department, Faculty of Science, Ain Shams University, Abbasia, Cairo, Egypt
Correspondence to: M. S. Abd El Keriem, Physics department, Faculty of Science, Ain Shams University, Abbasia, Cairo, Egypt.
| Email: |  |
Copyright © 2015 Scientific & Academic Publishing. All Rights Reserved.
In the work, optical behavior of cellulose triacetate films and related parameters are investigated under the effect of low dose gamma irradiation. The irradiation by a 10 kGy got success to reduce the refractive index of the cellulose triacetate polymeric film to reach 10.3% of its original value. At this irradiation dose the material dispersion is decreased by 65% associated with a reduction of 64% in the ratio between carrier density to the effective mass of carrier. The average oscillator strength and the average interband oscillator wavelength are suffered also drop of 36% and 15.3% in their initial values, respectively. An increase of about 18.6% in the band gap energy is achieved also with a dose of 10 kGy. The chemical bond approach and electronic polarizability are used to analysis and explain the results.
Keywords: Gamma irradiation, Cellulose triacetate, Dispersion
Cite this paper: M. S. Abd El Keriem, Effect of Low Gamma-Irradiation Doses on Cellulose Triacetate Polymer Films: I. Dispersion Properties, American Journal of Materials Science, Vol. 5 No. 2, 2015, pp. 41-46. doi: 10.5923/j.materials.20150502.03.
Article Outline
1. Introduction
- Conjugated polymers with alternating C=C and C–C bonds along the polymer backbone are important for space development and the design of fusion reactors [1, 2]. They have also a variety of advanced optical, optoelectronics and photonics applications [3]. Since the advances in electrical telecommunication and information processing are approaching their physical limits, therefore, to achieve processing rates greater than 50 GHz polymeric-based optical technologies are definitely required [4].Polymers are increasingly recognized as significant photonic and bio-photonic materials due to their molecular structure tailoring abilities [5]. Beside their ability to produce nano-objects as building blocks for nanotechnologies [6], surface functionalization, pre- and post-doping of the bulk-phase and producing inorganic–organic hybrid structures expand the function of polymers for photonics industry.Cellulose triacetate (CTA) as a polymeric material has important scientific and technological applications [7]. On the other hand, gamma irradiation can lead to a significant alteration in the structure and physical characteristics of the polymers. Accordingly, the optical properties of CTA have been studied under different preparation processes and treatments [8-12]. In this work the effect of low gamma irradiation on the dispersion and on dispersion related parameters of CTA films using the Fresnel spectro-interferometric-based technique [13] is carried out.
2. Experimental
2.1. Film Samples
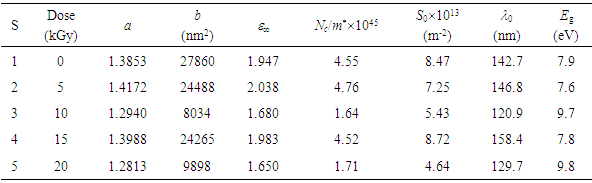
- Cellulose triacetate with the chemical formula [C6H7O2(OOCCH3)3]n is made from cellulose [14] by heterogeneous acetylation of the corresponding respective cello-oligosaccharide and purified by recrystallization twice from ethylacetate–hexane. All the six OH groups in the cellobiose units of cellulose are substituted by six COOCH3 groups, see Fig. 1. It is usually an amorphous polymer and rigid as supposed from the molecular structure. Developed Fortepan photographic film plates (Forte Photochemical Co. Ltd., Vác, Hungary) with dimensions of 6.3 cm × 8.8 cm and thickness of 180 ± 1 μm are studied. Table 1 records the different irradiation doses and the reference number of each sample used throughout the text and plots. The CTA film samples are irradiated by different gamma doses up to 25 kGy. A Cobalt source providing radiation flux of 275.6 rad/min is used.
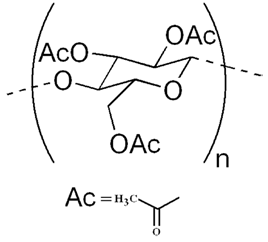 | Figure 1. CTA chemical formula |
2.2. Spectrometric Measurements
- Computer aided two-beam spectrophotometer (shimadzu-3101PC UV-VIS NIR) is used to record the reflectance, R, and the transmittance, T, data of plane-parallel polymeric film samples, A resolution limit of 0.2 nm and a sampling interval of 2 nm are utilized for the different measuring points, The accuracy of measuring R(λ), and T (λ) is 0.003 with the incident beam making an angle of 5.0± 0.1 to the normal to external slab faces. The measurements are carried out at room temperature for the entire spectral range 0.2-2.5 μm.
3. Results and Discussion
3.1. Structure Properties
- Figure 2 shows the x-ray curves for irradiated and nonirradiated cellulose triacetate films. All curves of polymeric films illustrate a single maximum approximately located at 26° correspond to the Van der Waals halo [15, 16]. This means that CTA films have mainly amorphous characteristics.
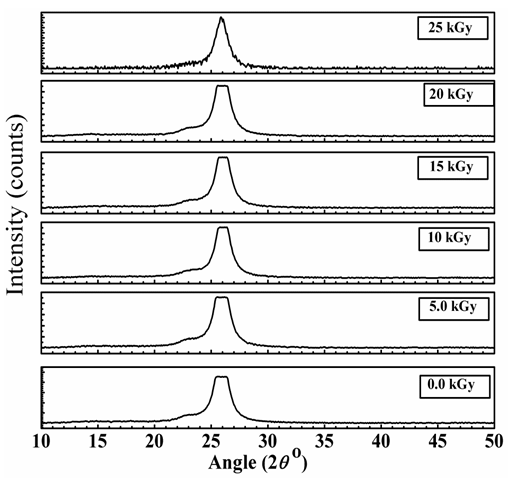 | Figure 2. X-ray curves of irradiated and nonirradiated CTA films |
3.2. Determination of Refractive Index
- Refractive index, n, is one of the fundamental physical parameter of the matter explaining its response to electromagnetic waves. It is closely related to the electronic polarizability of ions and the local field distribution inside the material network. The evaluation of the refractive index is important task to employ the materials for their proper applications. Furthermore, the refractive index is the key parameter for the optical device design [17]. Controlling the index of refraction, n, of polymers plays an imperative role in their advanced nonlinear optical and electro-optical applications as well as in nano-photonics and bio-photonic technologies.Fig. 3 illustrates the fitted refractive indices with Cauchy formula versus wavelength. The Cauchy formula has taken the form;
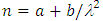 , where a and b are Cauchy constants of the studied material, see Table 1. It can be seen that there is obvious change in refractive index in split of the low used gamma irradiation doses. The obtained result is a sign of the effectiveness of the irradiation process on CTA. As seen in the figure, there is alternation in the index versus irradiation dose. Samples 1, 2 and 4 show a disparate increase in CTA index of refraction. A sharp decrease in the index of refraction is offered along with increasing the irradiation dose, as it seen with samples 3 and 5.
, where a and b are Cauchy constants of the studied material, see Table 1. It can be seen that there is obvious change in refractive index in split of the low used gamma irradiation doses. The obtained result is a sign of the effectiveness of the irradiation process on CTA. As seen in the figure, there is alternation in the index versus irradiation dose. Samples 1, 2 and 4 show a disparate increase in CTA index of refraction. A sharp decrease in the index of refraction is offered along with increasing the irradiation dose, as it seen with samples 3 and 5.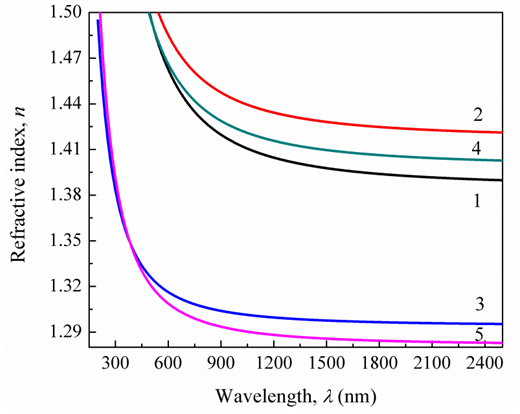 | Figure 3. Refractive indices versus wavelength |
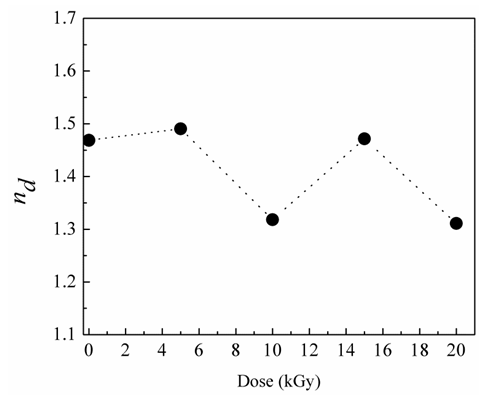 | Figure 4. Variation of refractive indices versus irradiation dose |
3.3. Material Dispersion Behavior
- The variation of n with respect to wavelength characterizes the dispersion properties of the material. The dispersion measurements are very significant for photonic materials, especially if the incident wavelength of the pump beam is around the band gap of the material. A positive Abbe number, Vd, specifies any transparent medium so that a material with a high Vd (i.e., low dispersion material) produces less chromatic aberration than one with a low Vd, where the reciprocal of the Vd is called dispersive power. Abbe number Vd is given by:
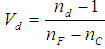 | (1) |
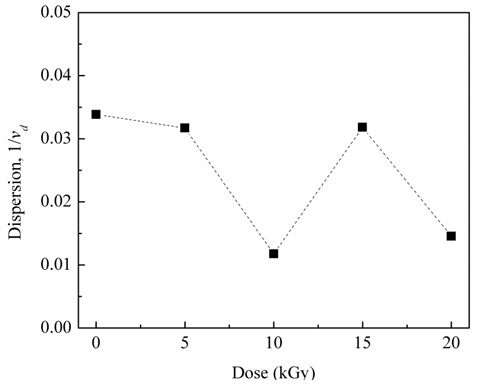 | Figure 5. Variation of material dispersion versus irradiation dose |
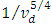 . Thus, the obtained reduction in material dispersion with such relative low value of irradiation dose gives the investigated polymer a possible resistance for damage due to Kerr nonlinearity (i.e., self focusing) which in turn expands the operational limits of polymers to be used in the industrial delivering high power laser system [22].
. Thus, the obtained reduction in material dispersion with such relative low value of irradiation dose gives the investigated polymer a possible resistance for damage due to Kerr nonlinearity (i.e., self focusing) which in turn expands the operational limits of polymers to be used in the industrial delivering high power laser system [22].3.4. Free Carrier Density
- To study the effect of gamma irradiation on the electronic polarizability of CTA films, and hence to understand the variation of determined refractive indices, the ratio of carrier density Nc to the effective mass m* of the carrier should be calculated. Consider the case of greater value of n than absorption index, the ratio of carrier density to the effective mass of the carrier (Nc /m*) is given by [23-25]:
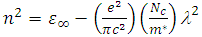 | (2) |
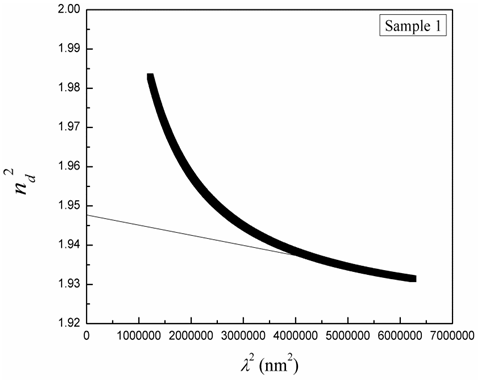 | Figure 6. Plotting n2 as a function λ2 to determine the ratio of carrier density to its effective mass |
3.5. Oscillator Model and Network Interband Characteristics
- To understand the nature of the obtained optical properties of the gamma-irradiated CTA polymer films, the dispersion properties will be explained using the single-oscillator model [26]. Several Sellmeier dispersion expressions are proposed depending on the number of considered oscillators one of them is given in the form of [27]:
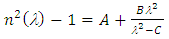 | (3) |
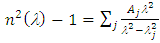 | (4) |
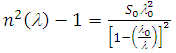 | (5) |
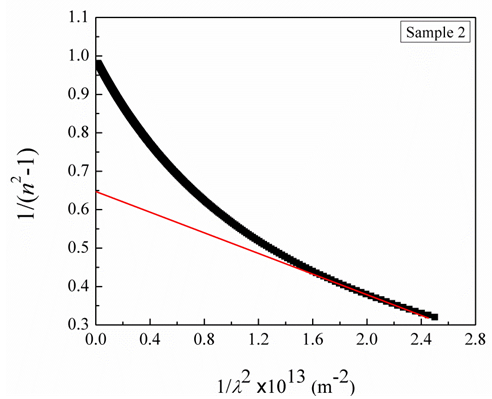 | Figure 7. Plotting of (n2(λ) – 1)-1 as a function of λ-2 to calculate both of average oscillator strength and the average interband oscillator wavelength |
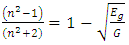 | (6) |
 -electrons which have the large electron mobility. Therefore it is easy for C=O
-electrons which have the large electron mobility. Therefore it is easy for C=O  electrons to demonstrate deformation of their electronic clouds by applying an electromagnetic field. Accordingly, irradiation dose for sample 3 was enough to decompose some of the C=O double bonds which have delocalized electrons with large electronic polarizability (1.020 Å3) into C-O bonds with their tightly bound electrons that have lower polarizability (0.584 Å3) [32]. Thus this transformation or decomposition of C=O bonds into C-O bonds which are associated with low electronic polarizability reflects itself in the recorded enlarging of band gap energy.
electrons to demonstrate deformation of their electronic clouds by applying an electromagnetic field. Accordingly, irradiation dose for sample 3 was enough to decompose some of the C=O double bonds which have delocalized electrons with large electronic polarizability (1.020 Å3) into C-O bonds with their tightly bound electrons that have lower polarizability (0.584 Å3) [32]. Thus this transformation or decomposition of C=O bonds into C-O bonds which are associated with low electronic polarizability reflects itself in the recorded enlarging of band gap energy.4. Conclusions
- A small dose of gamma irradiation of 10 kGy was enough to reduce potentially the refractive index and the material dispersion of cellulose triacetate polymeric film. An obvious reduction is determined in the values of the ratio of carrier density to the effective mass of the carrier, the average oscillator strength and the average interband oscillator wavelength. The band gap energy is raised up by 18.65% of its original value. These results confirm the sensitivity of cellulose triacetate and its optical properties for small gamma-irradiation doses. The used gamma irradiation doses are not sufficient to induce noticeable degradation or crosslink in the CTA backbone. Instead of that, it was enough to introduce, according to the dose, alternating remarkable changes in the chemical structure of the carbonyl groups converting some of them from having C=O bond into C-O bond or vice verse. This is adequate to the record fluctuation in physical properties of the polymer. The findings are key structural feature make cellulose triacetate polymer a promising candidate for applications in optoelectronics devices through the ability to manipulate delocalized π-electrons which are belong to carbonyl group by gamma irradiation processing.
References
| [1] | P. N. Prasad, J. E. Mark, and T. J. Fai, Ed. of “Polymers and Other Advanced Materials, Emerging Technologies and Business Opportunities,” V. N. Krishnamurthy, “Polymers in space environments,” (1995) 221-226. |
| [2] | H. Yamaoka, “Polymer materials for fusion reactors,” Recent Trends in Rad. Poly. Chem. Adv. Poly. Sci. 105 (1993) 117-144. |
| [3] | W. Barford, “Electronic and Optical Properties of Conjugated Polymers,” Oxford Univ. Press, 2013. |
| [4] | L. R. Dalton, A. W. Harper, B. Wu, R. Ghosn, J. Laquindanum, Z. Liang, A. Hubbel, C. Xu, “Polymeric electro-optic modulators: materials synthesis and processing,” Adv. Mater. 7 (1995) 519-540. |
| [5] | P. N. Prasad, “Polymer science and technology for new generation photonics and biophotonics,” Curr. Opin. Solid State Mater. Sci. 8 (2004) 11–19. |
| [6] | C. Park, J. Yoon, and E. L. Thomas, “Enabling nanotechnology with self assembled block copolymer patterns,” Polymer 44 (2003) 6725–6760. |
| [7] | N. Grassie, J. C. W. Chien, (ed) Proc. Conf. on Technique and Mechanism of Polymer Degradation and Stabilization, Elsevier, Karking, England; Polym. Degr. Stab. 25 (1989) 102. |
| [8] | S. A. El-Fiki, M. S. Abd El-Wahab, M. El-Sherief, S. A. Nooh, M. A. El Fiki, “Investigation of the effect of gamma rays on optical properties of polymers,” Radiat. Phys. Chem. 47 (1996) 761-764. |
| [9] | M. A. Khashan, A. Y. Nassif, S. A. El-Fiki, “Dispersion of the optical constants of cellulose triacetate irradiated by gamma rays in a wide spectral range 0.2–3 μm,” Opt. Commun. 208 (2002) 359–369. |
| [10] | F. El-Diasty, M. A. Soliman, A. T. Elgendy, A. Ashour, “Birefringence dispersion in uniaxial material irradiated by gamma rays: cellulose triacetate films,” J. Optics A: Pure & Appl. Opt. 9 (2007) 247-252. |
| [11] | F. El-Diasty, A. M. Bakry, “Spectroscopic and sub-bandgap optical properties of gamma-irradiated cellulose triacetate polymer,” J. Phys. D: Appl. Phys. 42 (2009) 145413-145417. |
| [12] | K. Songsurang, H. Shimada, S. Nobukawa, M. Yamaguchi, “Control of three-dimensional refractive indices of uniaxially-stretched cellulose triacetate with low-molecular-weight compounds,” Euro. Poly. J. 59 (2014) 105-112. |
| [13] | M. A. Khashan, A. M. El-Naggar, “A new method of finding the optical constants of a solid from the reflectance and transmittance spectrograms of its slab,” Opt. Commun. 174 (2000) 445-53. |
| [14] | M. A. Peterson, K. B. Lipkowitz, “Structure and dynamics of cellulose triacetate,” J. Mol. Strut.: THEOCHEM 395–396 (1997) 411–423. |
| [15] | N. S. Murthy, S. T. Correal, and H. Minor, “Structure of the amorphous phase in crystallisable polymers: Poly (Ethyleneterephtalate),”, Macromolecules 24 (1991) 1185–1189. |
| [16] | G. Vancso, D. Snetvy, and I. Tomka, “Structural changes during polystyrene orientation: A study of optical birefringence and wide angle X-ray scattering,” J. Appl. Polym. Sci., 42 (1991) 1351–1359. |
| [17] | M. Abdel-Baki, F. El-Diasty, "Glasses for photonic technologies," Inter. J. Opt. Appl. 3 (2013) 125-137. |
| [18] | D. C. Harris, M. D. Bertolucci, “Symmetry and Spectroscopy,” (New York: Dover, 1978). |
| [19] | Tsuyoshi Nakajima, Henri Groult, "Fluorinated Materials for Energy Conversion," Elsevier Ltd. 2005. |
| [20] | K. Jürgensen, “Dispersion-optimized optical single-mode glass fiber waveguides,” Appl. Opt. 14 (1975) 163-168. |
| [21] | N. L. Böling, A. J. Glass, A. Owyoung, “Empirical relationships for predicting nonlinear refractive index changes in optical solids,” IEEE J. Quantum Electron. 14 (1978) 601–608 (1978). |
| [22] | S. W. Allison, G. T. Gillies, D. W. Magnuson, and T. S. Pagano, "Pulsed laser damage to optical fibers", Appl. Opt. 32 (1993) 291-297. |
| [23] | E. Kh. Shokr, M. M. Wakkad, “Optical properties of Bi2Te2Se thin films,” J. Mater. Sci. 27 (1992) 1197-1201. |
| [24] | W. G. Spitzer, H. Y. Fan, “Determination of optical constants and carrier effective Mass of Semiconductors,” Phys. Rev. 106 (1957) 882-889. |
| [25] | M. M. Waakkad, “Effect of heat treatment on some of the optical parameters of Bi1.5Sb0.5Te3 thin films,” J. Phys. Chem. Solids 51 (1990) 1171-1176. |
| [26] | M. DiDomenico, S. H. Wemple, “Oxygen-octahedra ferroelectrics I. Theory of electro-optical and nonlinear optical effects,” J. Appl. Phys. 40 (1969) 720-734. |
| [27] | R. W. Ditchburn, “Light,” (New York: Dover, 1991). |
| [28] | G. Ghosh, “Sellmeier coefficients and dispersion of thermo-optic coefficients for some optical glasses,” Appl. Opt. 36 (1997) 1540-1546. |
| [29] | F. A. Moustafa, M. Abdel-Baki, A. M. Fayad, F. El-Diasty, “Role of mixed valence effect and orbital hybridization on molar volume of heavy metal glass for ionic conduction pathways augmentation,” Am. J. Mater. Sci. 4 (2014) 119-126. |
| [30] | M. Abdel-Baki, F. A. Abdel Wahab, A. Radi, F. El-Diasty, “Factors affecting optical dispersion in borate glass systems,” J. Phys. Chem. Solids 68 (2007) 1457-1470. |
| [31] | V. Dimitrov, T. Komatsu, “Classification of simple oxide: A polarizability approach,” J. Solid State Chem. 163 (2002) 100-112. |
| [32] | W. C. Oliver, G. M. Pharr, “An improved technique for determining hardness and elastic modulus using load and displacement sensing indentation experiments,” J. Mater. Res. 7 (1992) 1564-1583. |
 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML