1. Introduction

Double perovskites with general formula A₂B′B″O₆ with A being an alkaline earth such as Ca, Ba, Sr or a lanthanide and B′, B″ are the transition metals are a matter of investigation since past decades [1-7]. Kang et al. [1] have studied the electronic structure of Ba₂FeMoO₆ using photoemission spectroscopy. Borges et al. [2] investigated the ferromagnetic metallic behaviour of Ca₂FeMoO₆, Sr₂FeMoO₆ and Ba₂FeMoO₆with curie temperature of 345 – 426 K. Moritomo et al. [3-4] shows a strong correlation between the curie temperature and the conductivity at room temperature which implies that the mobile conduction electrons mediate the exchange interaction between the local Fe³⁺ ions. Sarma [5] has pointed out the discrepancies between the manganites and the double perovskites and proposed the mechanism of occurrence of large T_C in double perovskites Sr₂FeMoO₆. This mechanism has been extended to many other systems by Kanamori and Terakura [6-7]. In this model the hybridization of the Mo 4d (t_2g) and Fe 3d (t_2g) states plays the key role in stabilizing ferromagnetism at high curie temperatures [5-8] Based on band calculation using the Local Density approximation (LDA), Pickett [9] has proposed that the double perovskite La₂MnVO₆ can be a promising candidate for exhibiting half-metallic antiferromagnets (HM-AFM) characteristics. The electronic structure calculations were based on the assumption that both Mn and V ions are trivalent and more importantly a low spin state (t_2g⁴e_g⁰; S =1) resulted for all Mn³⁺ ions. Phillip et al. [10] studied the effect of structural changes and doping in the double perovskite A₂CrWO₆ (A = Sr, Ba, Ca) on the magnetotransport, the magnetic and optical properties together with band structure calculations. Phillip et al. have pointed out that the T_C in double perovskites was discussed to depend sensitively on band structure and band filling in contrast to experimental results [11].

In double perovskites having structural formula A₂B′B″O₆, each transition metal site (B′B″) is surrounded by an oxygen octahedron and the A atoms site are situated in the holes produced by eight adjacent oxygen octahedral. The properties of double perovskite compounds are determined by the relative sizes, valencies and ordering of the A and B site ions.

The study of elemental structures plays a pivotal role in solid-state physics [12]. The structural study gives insight into the properties of the elements. In the present paper, the electronic structure (density of states, band structure) of In₂ZnTiO₆ (IZT) are calculated by full potential linearized augmented plane wave (FLAPW) method [13] within the generalized gradient approximation (GGA) [14] as the material is a promising candidate for optoelectronic applications.

2. Computational Details

The ground-state properties of IZT are investigated employing the FLAPW method within the generalized gradient approximation (GGA). The structural parameters of the system were optimized at 2000-k points inside the irreducible Brillouin zone for integration. The full geometrical optimization gives an in-plane lattice constant a = b = c = 8.0 and c/a = 1.0 of pure In₂ZnTiO₆. Accurate optimizations of crystal geometries have come to serve as a stringent test for electronic structure calculations. We use our optimized parameters for the study of electronic structure calculations taking muffin tin radius (RMT) as 2.0, 1.9, 1.8 and 1.6 for In, Zn, Ti and O respectively. The total energy has been minimized and calculated with respect to the volume. In our calculation, the crystal structure of IZT has the space group symmetry Fm-3m. The Birch-Murnaghan relation for equation of state (EOS) is used to get the static equilibrium volume V₀ (=940.39) as well as the bulk modulus B₀ (= 123.55 GPa) and its pressure derivative B (= 3.0873) at zero pressure.

3. Results and Discussion

In figure 1, we have calculated and minimized the total energy with respect to the volume. In our calculation, the crystal structure of IZT has the space group symmetry Fm-3m. The Birch-Murnaghan relation for equation of state (EOS) is used to get the static equilibrium volume V₀ (=940.39) as well as the bulk modulus B₀ (= 123.55 GPa) and its pressure derivative B′ (= 3.0873) at zero pressure. The pressure derivative of bulk modulus at zero pressure B₀′ is a parameter of great physical significance in high pressure physics. It is related to a few other important thermo physical properties (like phase transitions, interphase energy, adsorption energy etc.) [14].

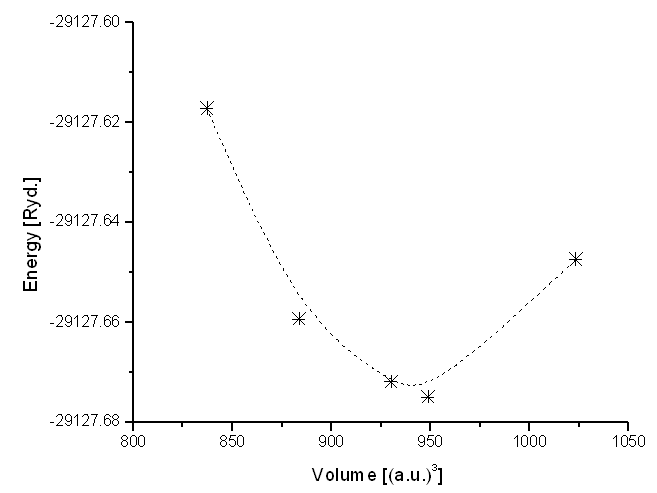Figure 1. Total Energy of In2ZnTiO6 as a function of cell volume

The calculated band structure for IZT in the high symmetry direction in the Brillouin zone is shown in figure 2. In this figure, we find a large dispersion of the bands. It can be seen that there are many bands from –3 eV to 1 eV. These bands are mainly contributed from Ti-d and O-p electrons. These bands also overlap each other at and around the Fermi level which indicates that there is hybridization between the Ti-d and O-p states. Comparing it with figure 3, it supports our explanation.

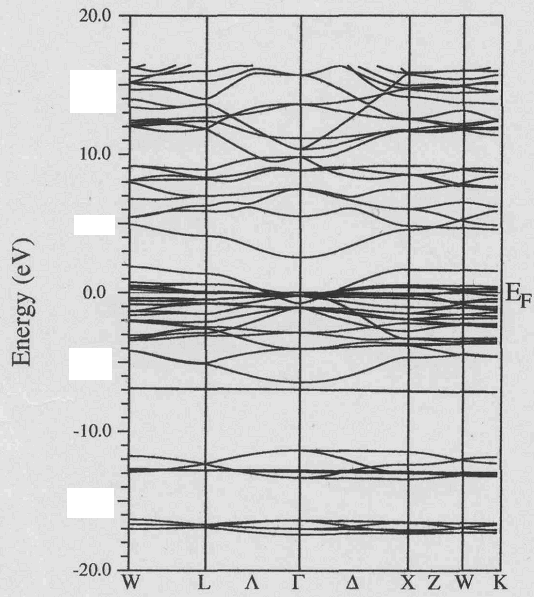Figure 2. The electronic band structure of In2ZnTiO6 along high symmetry directions

The angular momentum projected densities of states were obtained by using 2000-k points inside the irreducible Brillouin zone for integration. The full geometrical optimization gives an in-plane lattice constant a = b = c = 8.0 and c/a = 1.0 of pure In₂ZnTiO₆.

Figure 3 shows the total DOS along with partial DOS of Ti-d and O-p states of IZT. It is observed that the main contribution in the valence band comes from Ti-3d state. The Ti-d state hybridizes with O-p states near Fermi level. The hybridization between Ti-d and O-p states implies that the interaction between the atoms of these two is highly covalent. Titanium has excellent strength to weight ratio, high melting temperature and good corrosion resistance which render it suitable for light-weight, high temperature applications [16]. The tensile and fatigue strength of Ti increase with oxygen content at the cost of compromising ductility and toughness [17, 18]. These changes in mechanical properties are attributed to the interstitial oxygen atoms impeding dislocation motion and suppressing low temperature twinning [19]. Understanding mechanisms underlying this effect of oxygen is thus important from both scientific and industrial points of view.

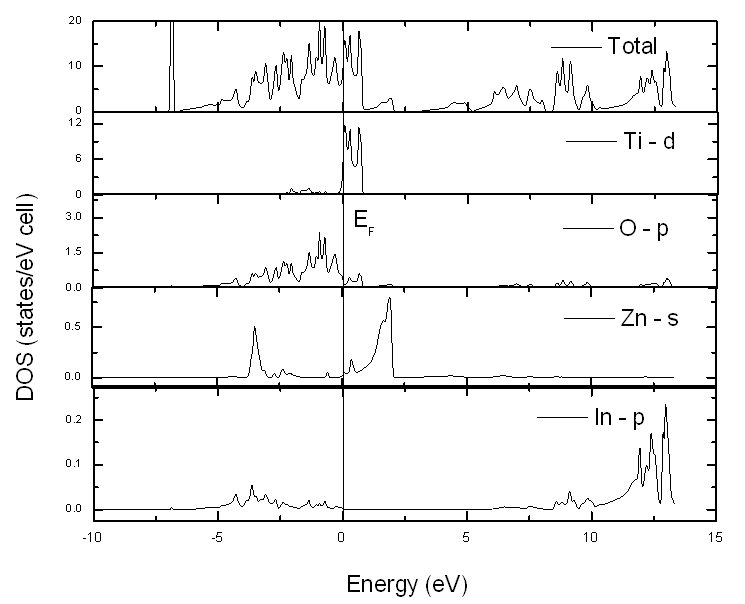Figure 3. Total DOS and PDOS around Fermi energy of In2ZnTiO6 calculated for the optimized lattice constant

Figure 4 represents the electron density distribution of In₂ZnTiO₆ in 100 planes. In figure 4, we can see that the interaction between Ti-d and O-p states is very strong. It implies the strong hybridization between these two states.

Figure 4. The electron density distribution of IZT in the (100) plane

4. Conclusions

We have performed and analyzed the FLAPW calculation of the double perovskite In₂ZnTiO₆ (IZT). The ground state and electronic structural properties have been obtained. From the angular momentum projected densities of states at 2000-k points inside the irreducible Brillouin zone for integration, it can be concluded that Ti-d state hybridizes with O-p states near Fermi level and the interaction between the atoms of these two is highly covalent which is further supported by the electron density distribution of In₂ZnTiO₆ in 100 plane.

ACKNOWLEDGEMENTS

The financial support rendered by the DAE-BRNS, Mumbai, India is gratefully acknowledged.