1. Introduction

Doped beta-rhombohedral boron (β-B) is a promising high-temperature semiconducting material useful for various technical applications, especially as an effective thermoelectric [1]. Unlike the conventional crystalline semiconductors Ge, Si, GaAs, etc., in which the constituting atoms placed in lattice regular sites are substituted with dopant atoms, in β-B any attempt to make substitutional doping with some non-metallic elements faces several obstacles. The reason is that real β-B crystals contain very high concentrations of intrinsic structural defects dominating in the formation of the electronic properties of undoped material. Consequently, β-B is characterized by a low sensitivity to doping: to achieve a desired effect it is necessary to introduce impurities with concentrations comparable with that of native defects. However, replacing such a high number of boron atoms in regular sites by foreign atoms leads to lattice destruction and / or formation of phase inclusions. Fortunately, in β-B it is possible to realize a fundamentally different mechanism of doping. The fact is that the complex crystalline structure of β-B with 105 regular atomic sites in the unit cell constructed from the icosahedral aggregates is characterized by a variety of different crystallographic voids sufficiently large to accommodate metal atoms with very slight structural distortions. We should emphasize that here we are not discussing pores, i.e., bulk structural defects, but we mean large intersites existing in a perfect crystal.

Such a mechanism of doping has several advantages compared with the conventional substitutional doping:

• A number of metallic impurities in β-B boron crystallographic voids can be introduced to the concentrations of several atomic percents;

• Because of a diversity of void types, which can accommodate atoms of the same chemical element, doping can simultaneously affect different physical properties of material;

• Since atoms of various chemical elements can be distributed in different ways between voids of different types, the same effect can be achieved by double, triple, etc. doping of boron by combining two or more elements.

Nowadays the influence of many metallic elements – Li, Mg, Al, Sc, Ti, V, Cr, Mn, Fe, Co, Ni, Cu, Zr, Nb, Hf, Ta, and Re – introduced in different crystallographic voids on some structural and ground-state, as well as electronic properties of β-B are studied experimentally. From these studies, one can make a general conclusion that metal M atoms in the β-B crystalline lattice usually fill voids of types A (mainly A(1)- and rarely A(2)- or A(3)-subtypes), D and E (their crystallographic description see in [2]). However, the lack of theoretical studies both on the interstitial doping mechanism and on the influence of interstitial doping on the β-B electron energy spectrum largely impedes the purposeful design of semiconductor materials based on solid solutions of metals in β-B. The investigation focused on calculation of the binding energy of metallic impurities localized in the crystallographic voids of the β-B lattice and their electron energy levels together with an analysis of the corresponding experimental data is presented elsewhere [3].

However, doping aimed at modifying electro-physical parameters at the same time affects other properties of the material. In particular, metal impurities being introduced at a high concentration in β-B crystal also serve as effective scattering centers for heat-carrying phonons reducing significantly thermal conductivity of the material and improving in this way its thermoelectric figure-of-merit. This paper is an attempt to determine vibrational modes localized on metal impurity atoms, accommodated in large crystallographic voids of the β-B lattice.

2. Theory

The values of the vibration frequencies of various interstitial metallic impurities in the β-B crystal lattice have been calculated by a quasi-classical-type method, which was developed earlier by us [4]. Then, quasi-classical interatomic potentials have been successfully used for calculating the ground-state parameters, including vibrational energies, of highly important boron-containing materials such as boron nitride BN molecular, crystalline and nanostructural modifications [5-14], and bare boron nanotubes [15, 16], as well as for examining some boron isotopic effects in solids [17-20].

2.1. Quasi-Classical Parameterization of Electron Charge Density and Electrical Field Potential Distributions in Boron and Dopant Metal Atoms

Since the advent of the Bohr model for a hydrogen atom, semi-classical models of light atoms have been constructed to advantage. The effectiveness of this approach in describing the periodic motion of electrons in small-sized molecules has been demonstrated as well. For many-electron systems, a reasonable accuracy can be achieved in terms of the self-consistent-field (SCF) approximation by finding extrema of the total energy functional in the class of quasi-classical wave functions. As for the heavy atoms, they can be calculated in the framework of the density functional theory (DFT) using a quasi-classical expansion of the energy functional with the local density approximation (LDA) as its initial approximation. A similar method appears to be appropriate for atomic clusters and condensed phases too.

However, atomic, molecular, and crystal potentials do not satisfy the standard Wentzel–Kramers–Brillouin (WKB) quasi-classical condition due to singularities at nuclear sites and electron-shell effects. The success of the above approaches can be explained on the basis of the quasi-classical expressions obtained by Maslov for the energies of bound electron states. 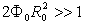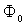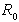It follows from these expressions that the exact and WKB spectra are close to each other irrespective of the potential smoothness when , where and are the characteristic values of the potential and its effective range, respectively (hereafter expressions and quantities will be given in atomic units (a.u.)).

Since the atomic orbitals at long distances are characterized by an exponential decay, the use of the modified Thomas–Fermi quasi-classical models makes it possible to parameterize the electron density distribution in an atom by introducing a finite atomic radius, 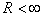, which is however considerably larger than the Bohr radius, 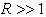, such that, at larger distances, the electron density is assumed to be zero. This is equivalent to the initial approximation in quasi-classical atomic models where the partial electron densities are ignored in classically forbidden regions. The radial potential 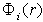of the effective field acting on the 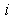th electron, 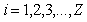, in the atom with the number 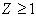can be represented by the Coulomb-like potential 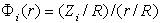, where 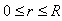and 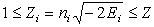is the effective charge dependent on the principal quantum number 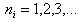and eigenvalue 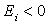of the energy of the state. Consequently, we have 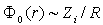and 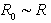, and the condition of quasi-classicality for the electron energy spectrum of an atom takes the form 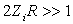. Therefore, atoms and the molecules and crystals formed by atoms are actually quasi-classical electronic systems in accordance with the Maslov criterion.

The potential energy of the 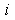th electron with orbital quantum number 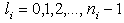is equal to 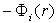. Therefore, the radii of the classical turning points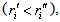

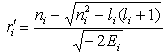and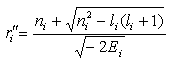

can be found as the roots of the equation

.

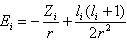Let be the potential of the field induced by the 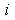th electron. Then, the potential of the field induced by the electron cloud of the atom can be written as the sum of these potentials:

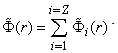The potential of the effective field acting on an arbitrary th electron of the atom is equal to the sum of the potentials of the Coulomb field of the nucleus and the field induced by all the electrons of the atom, except for the potential of the field of the electron under consideration:

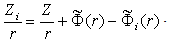Now we sum up these potentials over the electrons. As a result, the terms independent of the number of electrons on the right-hand sides are multiplied by the total number of electrons in the atom, 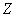, and the sum of the potentials 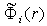gives 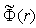. The solution of the obtained equation has the form

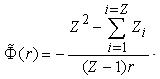This relationship makes it possible to determine the potential energy 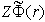of the interaction between the nucleus of the atom and the electron cloud. Since in the ground state their relative motion corresponds to a zero orbital quantum number, the radius of one classical turning point for this system is equal to zero and the radius 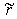of the other classical turning point is the root of the equation 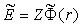, where 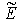is the eigenvalue of the energy associated with the relative motion of the electron cloud and the nucleus. If the effective fields acting on electrons are represented by Coulomb-like potentials, the effective field of the interaction between the nucleus and the electron cloud also turns out to be a Coulomb-like field. Further, under the assumption that the nucleus has an infinite mass and, hence, is stationary (i.e., the reduced mass of the nucleus-electron cloud system is equal to the total mass of electrons in the atom, 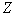), the radius of the turning point for the motion of the electron cloud with respect to the nucleus is given by the formula

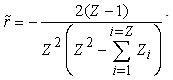The initial quasi-classical approximation implies that exponentially decaying partial electron densities are neglected in the classically forbidden regions, 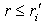and 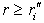, and that oscillations of these densities are ignored in classically allowed regions, 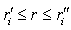. As a result the radial dependence of the direction-averaged partial charge density of the th electron state in the atom is represented by a piecewise constant function, which is equal to zero in the classically forbidden regions. A similar averaging for the motion of the electron cloud as a whole with respect to the nucleus is equivalent to averaging the nuclear charge over a sphere of radius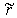. Summation of all the similar contributions gives the distribution of the total density of the electric charge in the atom in the form of a step radial function,

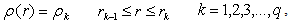where 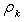are constants determined from the radii of the classical turning points and 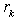coincide with these radii. Here, 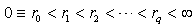and 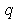is the number of layers with uniform charge densities. The parameter 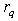plays the role of the quasi-classical atomic radius: the charge density is equal to zero at 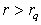. This representation is equivalent to volume averaging of the charge density in radial layers .

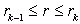Next, we calculate the fields induced by the charged layers with densities 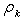making use of Gauss’s theorem and sum these fields. Then the atomic potential can be written in the form of a continuously differentiable piecewise analytical function. However, since the energy of the electronic system is a single-valued functional of the electron density, it is reasonable to approximate the obtained potential by a step function too. This can be adequately performed again by averaging over the volume: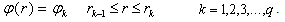

2.2. Quasi-Classical Calculation of Frequencies of Atomic Vibrations

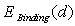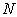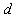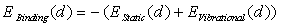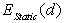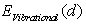The binding energy between an impurity metal (M) atom and surrounding boron (B) atoms placed at average distance can be written as , where and are the static energy of interaction of the cluster (except for the non-physical self-energy contribution) and the energy of the impurity atom vibrations relative to the surrounding boron atoms, respectively. In the initial quasi-classical approximation, these quantities are calculated from the following relations:

,

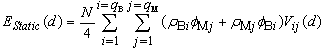and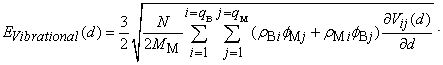

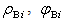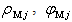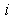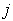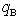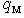Here () and () are the volume averages of the electric charge density and the electric field potential in the th and th radial layers of B and M atoms, respectively, and are the numbers of layers of the quasi-classical averaging in these atoms, and 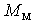is the mass of the impurity atom.

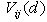denotes the volume of the intersection of 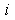th layer of the boron atom with the 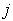th layer of the metal atom . It is calculated as a linear combination of intersection volumes of four pairs of spheres:

.

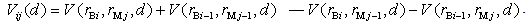As for the function 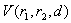, it has a geometric meaning as the volume of an intersection of two spheres with radii 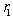and 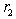whose centers are at the distance 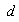from each other. This is an analytic (algebraic) piecewise continuous function:

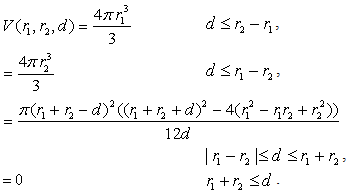Its partial derivative 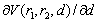is also continuous, but not continuously differentiable function:

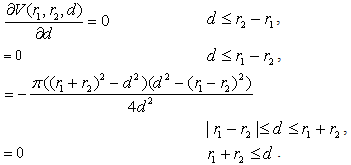The parameters 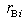and 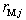are the external radii of the 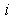th and 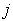th layers of boron and metal atoms, respectively (the inner radii are 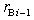and 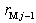, assuming 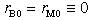). The parameters (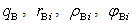) and (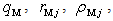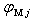) are assumed to be known.

Under the equilibrium conditions, the resultant force acting on an impurity atom from surrounding boron atoms has to be zero. This implies that in order to find the value of the binding energy of an impurity atom in different voids of the β-B crystal one should find extrema of the function 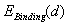. Note that one should consider both kinds of extrema, not only the binding energy maxima, which correspond to a stable equilibrium of the impurity metal atom surrounded by a group of boron atoms, but also the minima, that define the interatomic distances in unstable equilibrium. Since this cluster is not a closed physical system, but actually is embedded into the β-B crystalline lattice, the impurity atom localized at such an unstable equilibrium position cannot be kinetically capable to reach a stable equilibrium position. Obviously, one should take into account only the extrema, in which the binding energy is positive. Furthermore, one should confine oneself to the extrema for which the deviations of the average distances between the voids’ geometric centers (where the nuclei of the impurity atoms’ are supposed to be located) and the surrounding boron atoms are not too large compared with the predicted equilibrium lengths of M − B bonds.

One should not expect that the calculated M − B mean bonds length corresponding to an extremum must exactly coincide with the value actually realized in the crystal. It is likely to be an equilibrium bond length to which the subsystem tends. In the crystal, there is a specific M − B mean bond length for which the loss (gain) in the binding energy of an impurity with the lattice associated with the deviation of the cluster containing an impurity from its stable (unstable) equilibrium is compensated by the gain (loss) in the deformation energy of the rest of the crystal due to doping. Therefore, the binding energy values at its extrema may be well used to estimate the binding energy of an impurity atom with the crystal as a whole because, by definition of the latter, it is the difference between the total energies of a doped, and thus locally deformed crystal, and a pure ideal crystal. As 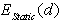is a main term in 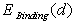the same is true for 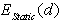. Then the vibrational energy correction 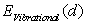at a binding energy extremum may be also well used to estimate the frequency of the impurity atom vibrations relative to surrounding boron atoms.

As it has been mentioned, on the one hand, binding energy is mainly determined by the static energy which is proportional to the linear combination of 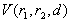-type functions and, on the second hand, at the extrema of the function 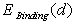its derivative should be equal zero, 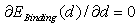. Consequently, expression under the square root in vibration energy formula containing linear combination of 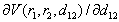-type functions usually changes its sign in the close vicinity of a binding energy extremum. But, the expression under the square root in the vibrational energy term is square of the required frequency of the mode localized at the impurity atom and when its value becomes negative it should be replaced by zero. This means that the numerical calculations will reveal a difference between left and right limits of the vibration frequency at the point of extremum: one of them will be positive, while the other will be zero. Therefore, it will be natural to estimate the frequency value at the extremum as the average of the left and right limits, i.e. half of the positive limiting value.

3. Results

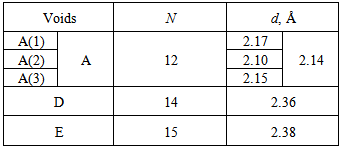
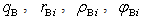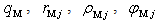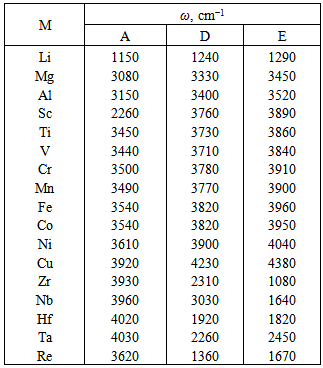
The vibration frequency was calculated for the 17 dopant metals listed in Introduction, which were found in A-, D- and E-type voids in β-B crystals. The used numerical values of quasi-classical parameters of boron and dopant metal atoms – and – have been pre-calculated and tabulated in [21]. The mean values of coordination numbers, , and the bond lengths (voids radii), , of atoms located in voids of type A, D and E of the β-B crystalline lattice are collected in Table 1. These numbers of neighbors are defined by the Lundström criterion [22], according to which atoms in this lattice are considered as nearest neighbors if the corresponding bond length does not exceed 2.80 Å. Taking into account that different impurity atoms placed in voids of different types deform the boron lattice structure, the values specified for the mean bond lengths should be treated just as indicative values.

The maximal bond length 2.80 Å introduced according to the Lundström criterion is by 0.42 Å larger than the mean radius of the largest (E-type) voids, 2.38 Å. We have used 1.65 Å as a possible lower limit of the M − B bond length, which is smaller approximately by the same magnitude than the mean radius, 2.10 Å, of the smallest (A(2)-type) voids, which can accommodate metal impurities.

The obtained vibrational frequencies are collected in Table 2. One can see that they are placed within the range from 1080 up to 4380 cm⁻¹.

Table 1. Parameters of Crystallographic Voids in β-Rhombohedral Boron

Table 2. Vibrational Frequencies of Metal Atoms Localized in Crystallographic Voids of β-Rhombohedral Boron

The approximations of the structural model used in calculations involve the determination of both the number of the nearest neighboring boron atoms and the bonding lengths of the impurity atom with its neighbors:

• Even in a perfect crystal, different boron atoms surrounding a void are located in crystallographically non-equivalent positions and at different distances from the geometric center of the void;

• Since β-B real crystals are characterized by a high concentration of intrinsic point defects in the form of vacancies, some atomic sites, where neighboring boron atoms are supposed to be found, actually may be unoccupied;

• The nearest neighbors of the impurity atom are counted according to the above mentioned Lundström criterion and, therefore, their number is arbitrary to some extent.

The relative error of the quasi-classical method itself when determining values of energy does not exceed a few percent. However, the model describing a cluster of a metal atom impurity and surrounding boron atoms is based on the above listed simplifications, which are necessary because of the complexity of the β-B lattice. Obviously they act as additional sources of calculation inaccuracies.

4. Discussion

Direct experimental verification of the theoretical findings of the present paper would be their comparison with the βB optical characteristics measured within the IR-region of spectrum. From the optical data (see, e.g., [23]), there are two bands in the β-B phonon spectrum placed at ~ 150 – 650 and 650 – 1050 cm⁻¹ which correspond to inter- and intra-icosahedral vibrations of boron atoms and their aggregates, and also the peak at ~ 1250 cm⁻¹ indicating stretching vibrations of the central atom in the unit cell. All of the vibration frequencies of impurity atoms calculated by us lie above these two bands and, therefore, they should be attributed to localized vibrational modes.

Unfortunately, there are almost no experimental data on localized modes which can be definitely identified as the vibrations of impurity atoms accommodated in crystallographic voids of β-B crystal. To our knowledge the only exception is the paper [24], where an absorption band detected near 2200 cm⁻¹ is reported. The intensity of this absorption band correlates with the tantalum (Ta) content in tested samples. Note that the placement of this band is well-consistent with the frequency of 2260 cm⁻¹ obtained by us for vibrations of Ta atoms localized in crystallographic voids of D-type. On the other hand, Ta atoms introduced in the β-B lattice are known to occupy predominantly just the D-type voids [1]. This coincidence speaks in favor of the plausibility of our results.

A more detailed, but indirect comparison between theory and experiment can be realized based on the thermal conductivity measurements performed in β-B samples doped with certain metals. As it has been noted in the Introduction, the analysis of the decrease in thermal conductivity, when β-B is doped with electrically active impurities, is an important task itself from the perspective of development of high-performance boron-based thermoelectric materials.

Let the atomic concentration of metallic impurities in voids of certain type equals to 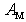, and 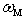is the frequency of the localized vibrations. We can introduce another parameter with the frequency dimension, 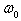, which characterizes the decay process of atoms displacements from their equilibrium positions in the structure. For the physically meaningful case, 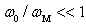, i.e., when the radius of the damping region of atomic displacements many times exceeds the wavelength corresponding to the atomic vibrations, the momentum relaxation time of heat-carrying phonons, 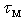, when they are scattered by localized vibrations with frequency of 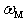, is determined [25] in the following form:

.

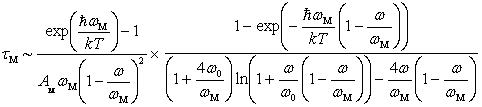Here 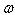denotes the frequency of a scattered phonon, while 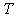is the sample’s temperature.

We can significantly simplify this relation taking into account that:

• In general, according to the above mentioned condition, the effective scattering of heat-carrying phonons by the localized vibrations occurs at ;

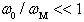• Locations of βB intrinsic phonon bands and vibration modes of impurities localized in lattice voids are such that the inequality 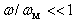holds for the characteristic phonon frequency .

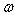• And finally, at room temperature, 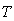≈ 300 K, the vibrational energy quantum of impurity atoms in βB significantly exceeds the thermal energy of the lattice vibrations, .

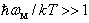Thus, for the dependence of the heat carriers’ momentum relaxation time 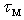on the parameters 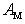and 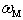characterizing scattering centers we will have:

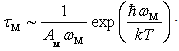Let us denote the maximum value of the thermal conductivity of undoped β-B samples at a certain temperature by 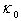. It is a value determined by the cumulative effect of all mechanisms of scattering of heat-carriers except for the scattering by localized vibrations associated with dopant atoms. If the coefficient of thermal conductivity 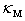, which takes into account the scattering by these localized vibrations as well, is calculated according to the Matthiessen’s approximate rule, i.e., by summing the reciprocals of thermal conductivities defined by various scattering mechanisms, we can write down

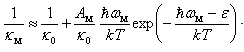In this formula, it has been introduced a parameter 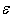with dimension of energy, which is dependent on the temperature , but not on and 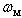. Solving this relation with respect to 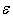, we obtain

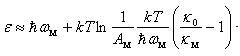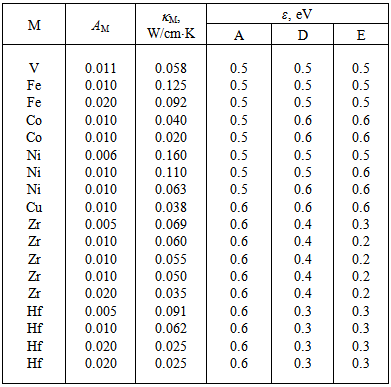
The available experimental data concerning the β-B heat-conductivity are as follows. At room temperature, the maximum thermal conductivity of undoped β-B is 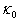≈ 0.276 W/K•cm. An introduction of a few percent of non-metallic impurities, such as 3.0 mol. % BaO, 2.9 at. % C and 4.8 at. % Si, leads to a reduction of this value to 0.200, 0.072 and 0.045 W/K•cm, respectively. A commensurable effect gives the doping of β-B with metal impurities again to the level of few atomic percent. These data are summarized in Table 3. For references to original works see the review [1].

Using these data as well as 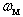frequencies calculated in this paper, we have estimated the parameter 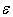for different metal atoms and different crystallographic voids of their placement. These results also are presented in the Table 3. It should be noted that, on the one hand, the atomic fraction of dopant metals as well as the room temperature thermal conductivity of doped β-B samples were known very roughly. Suffice it to say that in some cases, we evaluated 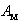from the weight composition of charges, from which the studied samples were melted, while most of 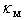values we had to find manually – from the thermal conductivity temperature-curves. On the other hand, the dependence of the term corresponding to the scattering by localized vibrations on the estimated parameter 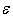is quite strong (exponential) and, consequently, 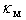must be sensitive to small changes in 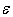. For these reasons, it makes little sense to calculate 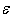with high accuracy. Table 3 shows the values of this parameter with preservation of only a single significant digit. Despite the approximations made in these calculations, their results may suggest some interesting hypotheses.

Table 3. Parameter of Scattering of Heat-Carriers by Localized Vibrations of Impurity Atoms and Room Temperature Thermal Conductivity in β-Rhombohedral Boron

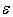This conclusion is backed by the fact that in most cases has almost identical values, ≈ 0.5 – 0.6 eV, which can be interpreted in such a way that all of the impurities, occupying voids of appropriate types, perform localized vibrations that effectively scatter heat-carrying phonons.

In addition, if the doping effects of a given chemical element for voids of any type can be described by almost the same parameter 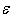, we can assume that those atoms in all possible positions act as almost identical scattering centers. The last is true for relatively light elements – V, Fe, Co, Ni and Cu – and it is due to the proximity of frequencies of vibrations of atoms localized within the voids of various types (see the Table 2). In such cases 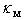will be almost independent of the distribution of impurity atoms among crystallographic voids of various types.

However, for relatively heavy elements, particularly, Zr and Hf accommodated in D- and E-type voids, we obtain lower values of the parameter 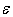with its wider spread, 0.2 – 0.4 eV. In such cases, the characteristics of distribution of impurity atoms between different voids will significantly affect . It should be associated with noticeable differences in frequencies of localized vibrations of heavy atoms when they are located in the voids of various types. One can see from Table 2 that these frequencies for Zr and Hf in A-, D- and E-type voids are 3930, 2310, 1080 and 4020, 1920, 1820 cm⁻¹, respectively.

Note that the measured values of thermal conductivity can be explained by the same 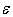as in the case of relatively light elements or Zr and Hf atoms in voids of type A, i.e. by 0.5 – 0.6 eV, if we assume that the concentration of these atoms in the voids of type D and E are significantly lower than the average concentration over the β-B crystal, i.e., if we assume that Zr and Hf impurities are predominantly concentrated in the voids of type A.

The available data on the distribution of metals among the β-B crystallographic voids are not entirely clear. However, it is interesting to note that structural studies of the measured samples doped with Zr and Hf indicate the high, low and middle occupancies of voids of type A, D and E, respectively, that is consistent with our interpretation. As for the relatively light elements, particularly Fe and Cu, for them the detected occupancies are quite different: low – high − very low and low − high − high, respectively. But in such cases, as it has been mentioned above, the distribution of impurities between voids should not have a significant effect on the thermal conductivity of the material.

The reason for the low occupancy of voids of type D and E by heavy elements are associated, on the one hand, with the instability of the equilibrium of these atoms in D voids, and, on the other hand, with large volume of E voids that are manifested in the binding energy of impurity atoms with β-B lattice being lower than the that of same atoms in A voids. These issues are addressed elsewhere [3].

5. Conclusions

In this paper we have theoretically determined vibration frequencies of 17 metal atoms – Li, Mg, Al, Sc, Ti, V, Cr, Mn, Fe, Co, Ni, Cu, Zr, Nb, Hf, Ta and Re – introduced in large crystallographic voids of type A, D and E existing in β-rhombohedral boron crystals.

It was found that these frequencies are expected in the range from 1080 to 4380 cm⁻¹, i.e., above bands of the intrinsic phonon spectrum. Consequently, the metals-doping of β-B should form the localized vibrational modes. In particular, the vibration frequency of 2260 cm⁻¹, calculated for Ta atom placed in a void of D-type, is in good agreement with the experimentally detected peak at 2200 cm⁻¹ in the optical absorption spectrum of β-B samples doped with tantalum, which in β-B lattice predominantly occupies just D-type voids.

A more detailed comparison with experiment has been implemented for thermal conductivity of β-B doped with metals such as V, Fe, Co, Ni, Cu, Zr and Hf. It has been demonstrated that the decrease in thermal conductivity in these samples can be consistently explained by the scattering of heat-carrying phonons by localized vibrations of impurity atoms. Thus, it was shown that doping of β-B can improve its thermoelectric figure-of-merit, not only due to the increase in its conductivity and, maybe in the Seebeck coefficient, but also by reducing its thermal conductivity.