-
Paper Information
- Next Paper
- Paper Submission
-
Journal Information
- About This Journal
- Editorial Board
- Current Issue
- Archive
- Author Guidelines
- Contact Us
American Journal of Materials Science
p-ISSN: 2162-9382 e-ISSN: 2162-8424
2014; 4(1): 7-10
doi:10.5923/j.materials.20140401.02
Study of the Behaviour of Critical Properties and Pinning Force in YBa2Cu3O7-δ
B. Lmouden1, A. Taoufik1, A. Tirbiyine2, M. Bghour1, A. Hafid1, A. Bouaaddi1, H. El Hamidi1, A. Labrag1, S. Senoussi3
1Laboratory of Superconductors Materials at High Critical Temperature, Ibn Zohr University, Agadir, Morocco
2Faculty poly-disciplinary, University Cadi Aayad, Safi, Morocco
3Laboratory of Solid Physics, Paris Sud University, 91405 Orsay Cedex, France
Correspondence to: B. Lmouden, Laboratory of Superconductors Materials at High Critical Temperature, Ibn Zohr University, Agadir, Morocco.
| Email: |  |
Copyright © 2012 Scientific & Academic Publishing. All Rights Reserved.
In this work we have studied the critical properties of YBa2Cu3O7-δthin films. We have examined the variation of Jc as a function of temperature for different values of a fixed magnetic field. This investigation shows that, in the absence of thermal activation and for the weaker values of magnetic field, Jc exhibits a behaviour according to[1-(T/Tc)2]m’ with a critical exponent m’ varying with a variation of magnetic field. On the other hand, we studied the variation of m’ parameter with the pinning force variation for different value of magnetic field. More scaling formulas were used to adjust our results in a large range of temperature and field, different parameters depending on the pinning mechanism such as m, 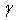 , n and
, n and 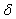 were determined. m and
were determined. m and 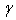 represent respectively the temperature and magnetic field dependence. Moreover, the values of m are related to the pinning force variation. The calculated value of n is compared with other investigations results, n is a good parameter reflecting the anisotropy of superconductor’s.
represent respectively the temperature and magnetic field dependence. Moreover, the values of m are related to the pinning force variation. The calculated value of n is compared with other investigations results, n is a good parameter reflecting the anisotropy of superconductor’s.
Keywords: Superconductor YBaCuO, Critical properties, Critical current density, Pinning mechanism
Cite this paper: B. Lmouden, A. Taoufik, A. Tirbiyine, M. Bghour, A. Hafid, A. Bouaaddi, H. El Hamidi, A. Labrag, S. Senoussi, Study of the Behaviour of Critical Properties and Pinning Force in YBa2Cu3O7-δ, American Journal of Materials Science, Vol. 4 No. 1, 2014, pp. 7-10. doi: 10.5923/j.materials.20140401.02.
Article Outline
1. Introduction
- In order to explain the mixed state of a HTc superconductors, several researchers have studied the dynamic of the vortices. When a current is applied to a superconductor sample, the flux lines become in motion above a critical current density Jc threshold below which the flux lines are pinning.The critical current density Jc is one of the most important parameters for application of superconductor materials. In the absence of thermal activation of flux pinning, the expression of Jc as function of temperature and magnetic field is[1]:
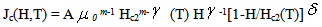 m,
m, 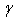 and
and 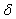 are parameters depending on the pinning mechanism, A is a constant. The upper critical field is expressed as function temperature with:
are parameters depending on the pinning mechanism, A is a constant. The upper critical field is expressed as function temperature with: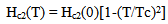 For the weak values of magnetic fields, the expression of Jc is given as:
For the weak values of magnetic fields, the expression of Jc is given as: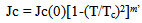 In this paper we will study the volume of pinning force of vortices in a superconductor type II. We will discuss the variation of pinning force with different applied magnetic field and we will determine the dependence of critical properties m and m’ to the pinning force on the Kramer model for weak magnetic field.n is depending on m and
In this paper we will study the volume of pinning force of vortices in a superconductor type II. We will discuss the variation of pinning force with different applied magnetic field and we will determine the dependence of critical properties m and m’ to the pinning force on the Kramer model for weak magnetic field.n is depending on m and 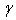 parameters, several investigations show that n is a parameter in expression of irreversibility field Hirr with Hirr is proportional to[1-(T/Tc)]n . The value of n is a factor of film quality and strength flux pinning .In this work, we will determine the value of m,
parameters, several investigations show that n is a parameter in expression of irreversibility field Hirr with Hirr is proportional to[1-(T/Tc)]n . The value of n is a factor of film quality and strength flux pinning .In this work, we will determine the value of m, 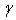 ,
, 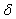 and n for our YBa2Cu3O7-δ film.
and n for our YBa2Cu3O7-δ film.2. Experiments
- The studied sample is a monocristalline YBaCuO thin film deposited by the ablation laser method on the surface (001) of a SrTiO3 substrate. In zero magnetic field, the resistance vanished a Tc= 90K. The C-axis of YBaCuO is perpendicular to surface on the film. Electrodes of measurement are in gold and deposited on the surface of the sample in situ by evaporation. The film has a thickness of 400 nm, and a width 7.53 µm. The distance between electrodes of power measurement is 135 µm. Contact resistances were less than 1 Ω[2]. A direct current, perpendicular to the magnetic field, is applied on edge of the sample.
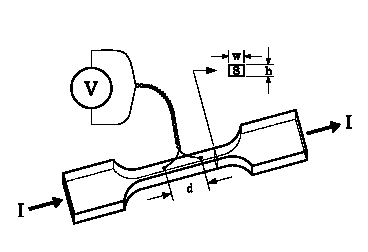 | Figure 1. Schematic representation of the sample with the electrical contacts of transport measurements d = 135 μm, h = 400 nm, w = 7.53 μm |
3. Experimental Results and Discussion
- In figure 2, we shown the variation of critical current density Jc as function of 1-t2 with t=T/Tc, at different values of constant magnetic field. With the use of a linear fitting, we have determined the exponent m’ for each value of the magnetic field.
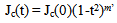 | (1) |
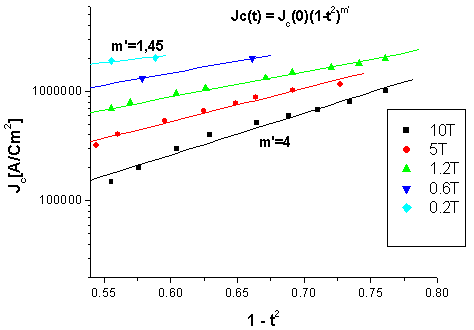 | Figure 2. Variation of Jc as function as 1-t2, t=T/Tc |
|
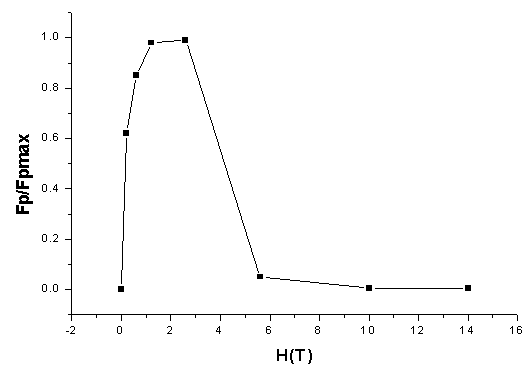 | Figure 3. Variation of volume density of pinning force as function of applied magnetic field H // c |
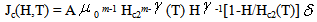 | (2) |
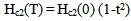 | (3) |
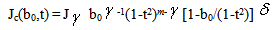 | (4) |
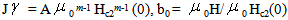 When the applied magnetic field is weak, we can neglect[1-b0/(1-t2)]
When the applied magnetic field is weak, we can neglect[1-b0/(1-t2)] 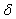 term and equation (4) scale as equation (1) with m’ = m-
term and equation (4) scale as equation (1) with m’ = m-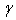 .When the applied magnetic field increases, the term[1-H/Hc2(T)]
.When the applied magnetic field increases, the term[1-H/Hc2(T)] 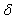 becomes effective.We have concluded that the expression of critical current density Jc for the lower values of magnetic field is:
becomes effective.We have concluded that the expression of critical current density Jc for the lower values of magnetic field is: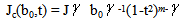 From Equation (1) we can write m’ = m -
From Equation (1) we can write m’ = m - 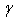 .The value of
.The value of 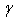 is depending on the temperature. However, the value of
is depending on the temperature. However, the value of 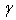 is constant for each value of temperature.From m = m’ +
is constant for each value of temperature.From m = m’ + 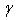 and for a constant value of temperature. When the value of m’ increases, the value of m increases too.We can conclude that in Kramer model for the lower values of magnetic field, the value of m increases with the increasing of pinning force. Subsequently, we will determine the value of n parameter in our sample. Referring to figure 1, we can determine the value of m’ (m-
and for a constant value of temperature. When the value of m’ increases, the value of m increases too.We can conclude that in Kramer model for the lower values of magnetic field, the value of m increases with the increasing of pinning force. Subsequently, we will determine the value of n parameter in our sample. Referring to figure 1, we can determine the value of m’ (m-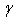 ) with the weakest magnetic field, equals to 1,45.Referring to literature, we can find that the value of
) with the weakest magnetic field, equals to 1,45.Referring to literature, we can find that the value of 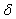 equals 2[5].Figure 4 shows the dependence of Jc as function magnetic field for each value of temperature.From figure 4, we can determine the value of
equals 2[5].Figure 4 shows the dependence of Jc as function magnetic field for each value of temperature.From figure 4, we can determine the value of 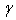 with a low value of temperature to avoid the flux creep. In figure 5, for a value of T = 50 and referring to Equation (4), we can observe that Jc depending of magnetic field as Jc(H)
with a low value of temperature to avoid the flux creep. In figure 5, for a value of T = 50 and referring to Equation (4), we can observe that Jc depending of magnetic field as Jc(H) 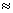 H-0.5.
H-0.5. 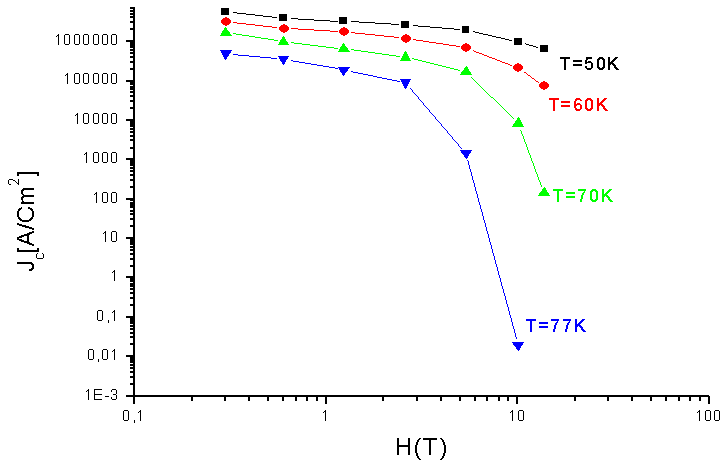 | Figure 4. Variation of Jc as function as magnetic field for different values of temperature |
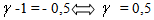 and m = m’ +
and m = m’ + 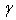 = 1,95.The expression of the n parameter mentioned above is given as[5]:
= 1,95.The expression of the n parameter mentioned above is given as[5]: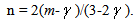 With m = 1.45 and
With m = 1.45 and 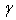 = 0,5, we can determine that the value of n equals to 1,45 (n ≈ 1,5).It’s known that the value of n increases with the degree of anisotropy of superconductors[6,7], according to other previous researchs, we find that the value of n in YBCO films is nearly equals 1,5[8,6].
= 0,5, we can determine that the value of n equals to 1,45 (n ≈ 1,5).It’s known that the value of n increases with the degree of anisotropy of superconductors[6,7], according to other previous researchs, we find that the value of n in YBCO films is nearly equals 1,5[8,6]. 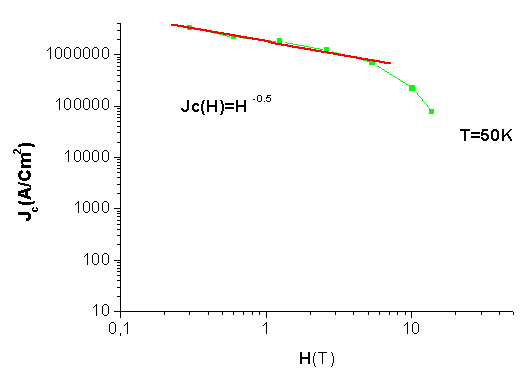 | Figure 5. Variation of Jc with magnetic field H for T= 50K |
4. Conclusions
- In this work, we have presented a research of some parameters of the YBCO high Tc superconductor such as m,
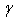 and
and 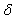 depending on pinning mechanism. The main results in this research are the dependence of the parameters m and m’ to the volume density of pinning force. In the Kramer model, for the weaker values of the magnetic field, m and m’ increase with the increasing of the pinning force. On the other hand, the result of the n parameter (n ≈1,5) in our sample with 400 nm of thickness is estimated to be in consistence with other author’s finding.
depending on pinning mechanism. The main results in this research are the dependence of the parameters m and m’ to the volume density of pinning force. In the Kramer model, for the weaker values of the magnetic field, m and m’ increase with the increasing of the pinning force. On the other hand, the result of the n parameter (n ≈1,5) in our sample with 400 nm of thickness is estimated to be in consistence with other author’s finding.ACKNOWLEDGEMENTS
- I am very grateful to all authors team who have contributed to achieve this work and for their help during the preparation of this draft.
 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML