-
Paper Information
- Next Paper
- Previous Paper
- Paper Submission
-
Journal Information
- About This Journal
- Editorial Board
- Current Issue
- Archive
- Author Guidelines
- Contact Us
American Journal of Materials Science
p-ISSN: 2162-9382 e-ISSN: 2162-8424
2013; 3(4): 70-76
doi:10.5923/j.materials.20130304.02
Hole Dangling Bond Capture Cross-Sections in aSi:H
David M. Goldie
Division of Physics, University of Dundee, Dundee, DD1 4HN, United Kingdom
Correspondence to: David M. Goldie, Division of Physics, University of Dundee, Dundee, DD1 4HN, United Kingdom.
| Email: |  |
Copyright © 2012 Scientific & Academic Publishing. All Rights Reserved.
It is demonstrated that the occupation statistics for a Gaussian distribution of dangling bond states may account for the measured variation of hole mobilitylifetime values in hydrogenated amorphous silicon as the Fermi energy is systematically varied by doping from about 0.55 eV to 1.05 eV below the conduction band edge. An assessment of how the deduced dangling bond parameters may be influenced by underlying doping effects suggests that the minimum cross-section ratio for hole capture into charged (σh-) and neutral (σh0) dangling bond states requires that σh-/σh0 ≥ 5. The capture of holes is consequently dominated by charged dangling bonds provided the Fermi energy lies within the upper half of the band-gap. Both σh- and σh0 are observed to depend upon temperature (T) as σh ∝ T-β which may indicate the presence of tunnelling transitions between valence band tail states and dangling bonds.
Keywords: Amorphous Silicon, Dangling Bonds, Hole Capture Cross-Section
Cite this paper: David M. Goldie, Hole Dangling Bond Capture Cross-Sections in aSi:H, American Journal of Materials Science, Vol. 3 No. 4, 2013, pp. 70-76. doi: 10.5923/j.materials.20130304.02.
Article Outline
1. Introduction
- Danglingbonds (DBs) are presently believed to provide the major point defect in thin films of hydrogenated amorphous silicon (aSi:H)[1,2]. Their presence is detectable by a variety of experimental techniques where quantitative agreement on their overall density is generally found for samples that are grown using comparable deposition conditions. By contrast, the energetic distribution of DB states, and their effective capture rates for electron and hole carriers, has remained largely unresolved, with different experimental approaches yielding a significantly large spread of values[2,3]. Many of these discrepancies may possibly be related to underlying equilibration phenomena[1, 2], or may simply arise through the use of inappropriate DB recombination kinetics for the analysis of non-equilibrium charge carrier transport[4-6]. In particular there appears to be little consensus concerning the relative magnitude for the capture cross-section ratio between charged and neutral DB defects[4-16] despite this being central to the interpretation, modelling and performance optimisation of all a-Si:H optoelectronic devices.The present work considers whether a fixed Gaussian distribution of DB states, originally proposed for the interpretation of electron lifetime results[17-19], is also appropriate for the analysis of hole (h) capture data. Owing to the anomalously dispersive character of the hole carrier transport, however, the quantity now considered is the hole mobilitylifetime product (µτ)h. The DB density of states (DOS) parameters derived from the previous electron study are initially employed as a constraint in the present analysis and only the relative crosssections for hole capture into singly-occupied neutral DB states (σh0), and doubly- occupied charged DB states (σh-), have been adjusted in attempting to fit the experimental results. By relaxing this constraint, and allowing the DB energies to shift in response to the Fermi energy, a realistic range of DB DOS parameters, and associated σh-/σh0 ratios, are generated. The underlying physical origin of the inferred σh-/σh0 ratios is subsequently explored by studying the temperature dependence of the hole capture processes into the neutral and charged DB centres.
2. Experimental Details
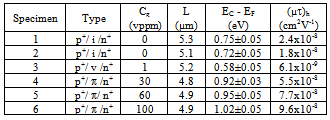
- Details of the aSi:H samples used in the present work are summarised in Table 1. All specimens were deposited by plasma enhanced chemical vapour decomposition (PECVD) of silane gas onto glass substrates held at a temperature of about 290℃. The PECVD reactor conditions used during capacitively-coupled deposition were: RF power = 8 W at 40 MHz; partial chamber pressure = 150 mtorr; gas flow rate = 8 sccm. Systematic n-type and p-type doping of the a-Si:H films was respectively achieved through the controlled addition of phosphine or diborane in precisely determined volume parts per million (vppm) amounts during the PECVD growth process. Sample growth rates were typically about 1 Ǻs-1 and the films were generally sandwiched between 300 Ǻ thick heavily doped p+ and n+ layers to form diode junction structures (p+/ i /n+ for undoped films, p+/ ν /n+ for n-type films and p+/ π /n+ for p-type films). The film thicknesses (L) were sufficiently large (≈ 5 µm) to ensure that the measured (µτ)h values were representative of the true bulk magnitude and not influenced by contact complications[20].Charge collection measurements were performed using a standard timeofflight (TOF) arrangement[1,2,21] with the diode devices subjected to a pulsed reverse voltage bias (Vr). Excess hole carriers were then generated in the vicinity of the n+ layer using a 5 ns dye laser operating at a wavelength of 570 nm which was synchronised to fire a short time (~50 µs) following the application of Vr. Experiments were performed under small-signal conditions and the amount of collected charge was subsequently obtained by numerical integration of the resulting transient photocurrents. A standard Hecht analysis[1] finally allowed the mobilitylifetime products of the hole carriers to be determined. Data for (µτ)h was recorded between temperatures (T) of 260 K and 425 K by mounting the samples in an evacuated cryostat. The location of the Fermi energy (EF) relative to the conduction band edge (EC) was estimated from the activation energy of dark conductivity measurements performed on the i, ν and π diode layers which were rendered devoid of the p+ and n+ layers by shielding selected substrates during the PECVD process.
|
3. Results and Discussion
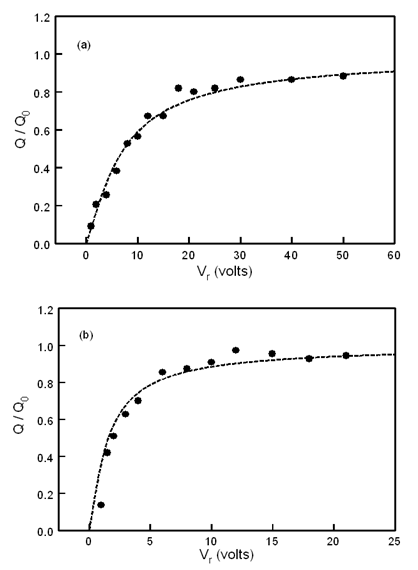
- Examples of charge collection data are given in Figure 1 which shows how the amount of collected hole charge (Q) approaches a limiting saturated magnitude (Q0) as the reverse diode potential Vr is progressively increased. Under small-signal conditions Q0 was typically restricted to less than 10 pC. The solid curves in Figure 1 represent the optimum fit of the data to the Hecht formula[1] which allows (µτ)h to be extracted according to:
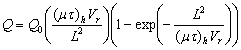 | (1) |
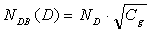 | (2) |
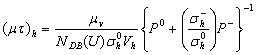 | (3) |
3.1. Fixed DB DOS Analysis
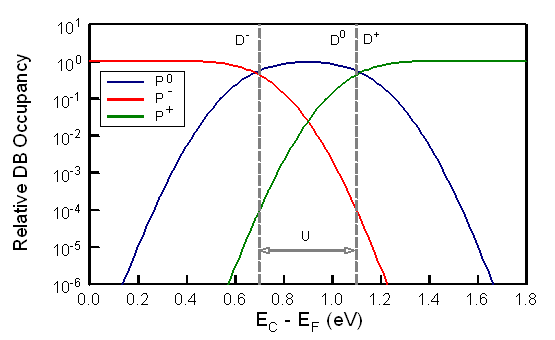
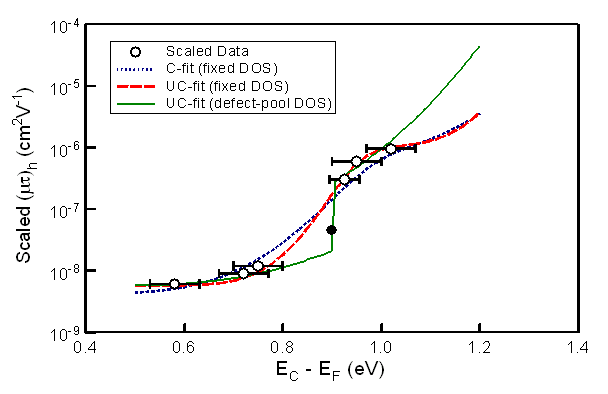
- For consistency with the previous electron work[19] both the D0 and D- states were initially assumed to have a Gaussian energy distribution with standard deviations S = 0.10 eV. The mean energy of the D0 state (ED) is located at EC - ED = 1.10 eV so that with a positive correlation energy U = 0.40 eV the D- state is located 0.70 eV below EC. Adopting these fixed DB DOS values the ensuing variation of P0 and P- upon the Fermi energy position is depicted in Figure 2 for T = 295 K. For completeness the relative density P+ of the D+ DB states is also plotted in Figure 2 since for all Fermi energy locations P0 + P- + P+ = 1.By constraining the DB DOS the only quantity which may be adjusted in Equation 3 to fit the dependence of the experimental data upon EF is the magnitude of σh-/σh0. An example of the fitting procedure is shown in Figure 3, where the plotted (µτ)h points for the doped specimens have been adjusted by the scaling requirement described above to account for the incurred doping enhancement of NDB according to Equation 2. The value of the scaling factor clearly depends upon knowledge of NDB(U) for the undoped p+/ i /n+ specimens and for the data plotted in Figure 3 corrections have been applied for NDB(U) = 1.2x1016 cm-3. The effect of the selected NDB(U) magnitude upon the DB parameters that are returned by the analysis is discussed later.
3.2. Defect-Pool DB DOS Analysis
- To perform an equivalent analysis using the defect-pool DOS model it is now necessary to allow the mean energy of the D0 state to shift relative to ED in the fixed DOS situation depending upon whether the material is n-type or p-type in nature so that[2]:
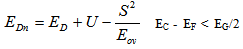 | (4a) |
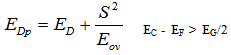 | (4b) |
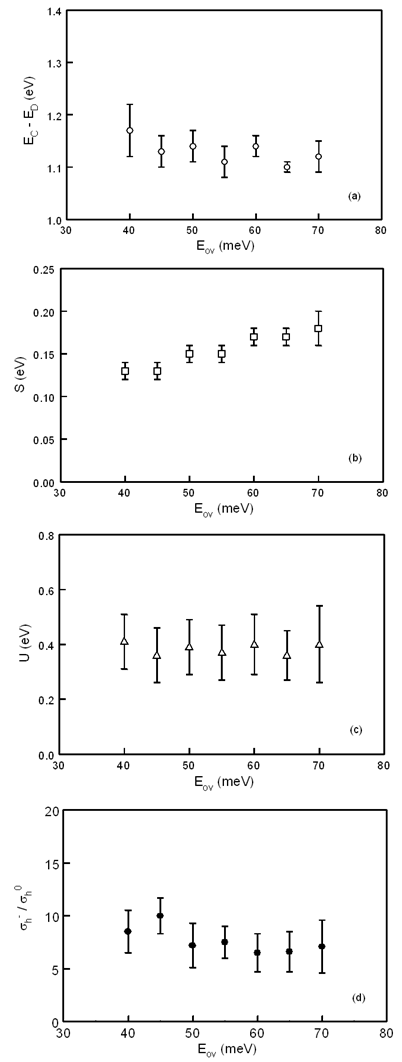 | Figure 4. The dependence of the fitted defect-pool DB DOS parameters upon the assumed value for Eov. (a) EC - ED (b) S (c) U (d) σh-/σh0 |
3.3. Temperature Dependence of Capture Cross-Sections
- Additional insight into hole capture by the D0 and D- states may be provided by examining the underlying temperature dependence of the cross-sections (σh(T)). From the electron work[18,19] the capture of electrons (e) by DBs was found to proceed by physically distinct mechanisms with the e→D0 capture being identified as a strong multiphonon emission process, whereas the e→D+ capture was interpreted as being Coulombic in nature. To experimentally investigate σh(T) it is noted from Equation 3 that as P0 and P- are only weakly dependent upon temperature through statistical shifts in EF[1], the main temperature influences are likely to arise from µv(T) and (µτ)h(T) so that σh(T) may be expressed as:
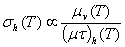 | (5) |
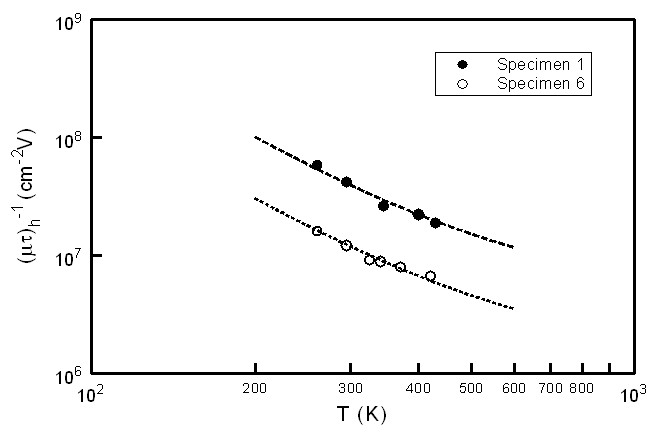 | Figure 5. Double logarithmic plots of (µτ)h-1 against temperature for specimen 1 and specimen 6. The dashed lines represent the best fit of Equation 6 to the data for which Eov = 45 meV |
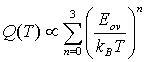 | (6) |
3.4. Capture Cross-Section Radii
- The absolute magnitude of the (µτ)h values that are generated by Equation 3 is determined by a pre-factor quantity µv / (NDB(U)σh0Vh) which is independent of EF and may therefore be used to provide an estimate for σh0, and subsequently σh- using the σh-/σh0 ratio. For the parameter set returned in Figure 4 it is found that µv / (NDB(U)σh0Vh) = 3.8 ± 0.6 x10-8 cm2V-1. Taking literature values for Vh = 107 cms-1 and 1 cm2V-1s-1 < µv < 10 cm2V-1s-1[1-3, 25] it is then found that 8x10-17 cm-2 < σh0 < 1x10-14 cm-2 for 3x1015 cm-3 < NDB(U) < 3x1016 cm-3. The capture radius for σh0 is thus estimated to lie between 0.5 Ǻ and 5.6 Ǻ, and with σh-/σh0 ≤ 10 the corresponding capture radius associated with σh- has a minimum value of 1.6 Ǻ. These capture radii accordingly fulfil the criterion for the use of a ballistic capture pre-factor in Equation 3 since the scattering length is estimated to be greater at around 2 Ǻ for the lower µv limit[24].
4. Conclusions
- The variation of experimental (µτ)h data with EF in a-Si:H is qualitatively consistent with a hole capture rate which is greater for charged compared to neutral DB states. The relative occupation density of D0 to D- states with EF may consequently be used to estimate the underlying magnitude for σh-/σh0. Quantitative fitting of the (µτ)h data using alternative DB DOS models reveals that the capture cross-section ratio σh-/σh0 may vary from greater than 170 (fixed DOS) to less than 10 (defect-pool DOS). Whilst the smaller σh-/σh0 values returned by the defect-pool DOS appear to be more physically plausible for a-Si:H there is presently insufficient experimental data to discount the fixed DOS possibility on quantitative model fitting evidence alone. The temperature dependence of the hole capture cross-sections suggests that the capture of holes by DBs is enhanced by valence band-tail tunnelling transitions at room temperature in a-Si:H.
 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML