1. Introduction

Small clear specimens are considered, with fibre direction in the longitudinal direction of the beams. The values of the bending strength are described in dependence of the span-depth ratio (span length L /specimen depth D). The specimens show flexural fractures above a critical value of the span-depth ratio and shear fractures below. Only the range of flexural fractures is examined in this paper.

The used loading configurations are centre loading and third-point loading (in some cases two-point loading).

Two special cases of the annual growth ring orientations are regarded, namely annual rings parallel (vertical annual rings) and annual rings normal to the direction of the load (horizontal annual rings).

The compression strength perpendicular to grain at the load points is important for flexural fracture. Deformations can reduce the bending strength.

2. Stress Distribution

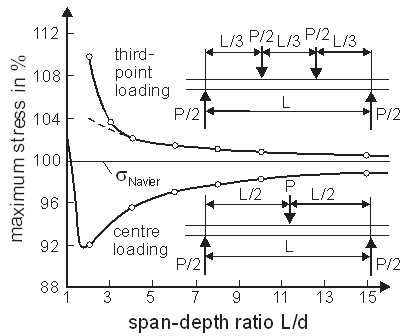
The classical(elementary) beam theory[1] supposes a linear distribution of the longitudinal stresses across the beam depth. The bending stresses calculated under these suppositions should be at the same time the stresses in the extreme fibres of the tension and compression zone. The graph of the bending stresses shows according to the beam theory for centre loadinga triangular and for third-point loading a trapezoidal shape a long the beam length. Salient points (kinks) should appear inthe graphs of these bending stresses. Consequently, they also show up in the graphs of the stresses at the extreme fibres of the tension zone. No such salient points can occur, if there are no external loads, effecting in the tension zone.

Seewald[2] calculated the stress distributions for beams under centre loading and third-point loading, supposing a linear elastic, homogenous, and isotropic material. The validity of the stress distributions calculated can be proved experimentally.

The stress distribution can be determined according to a method of Schneeweiß[3] and[4] experimentally in the following way: a great number of the same specimens is tested; the locations of the fracture origins are determined. The frequency distribution of the fracture origins is used to calculate the stress distribution. Fracture occurs mainly at or near the point of the maximum stress, and less often, where the stress is lower.

Fig. 1 shows as an example the frequency distribution of the location of fractureof 72 concrete specimens as a histogram. The specimens had a cross-section of 120 x 120mm². They were tested with a span length of L = 300mm under third-point loading. The mentioned methodin[3] and[4] results ina stress distribution with two maxima of the stress between the two load points, as can be seen in Fig. 1. This corresponds to the stress distribution calculated by See wald evaluated by Naschold[5] and Tucker[6]. The stress distribution for centre loading was also determined in[4], showing at the mid-span a stress distribution with a horizontal tangent instead of the salient point. Steinhardt[7] achieved such a stress distributio nusing the brittle lacquer test for beams of spruce.

Naschold[5] calculated the maximum tensile stress in beams as shown in Fig. 2. The maximum stress at third-point loading (the stress at both maxima) shall increase steadily with decreasing span-depth ratio. The maximum stress decreases for centre loading until L/d = 1.7, compared to the beam theory, and then increases strongly. The difference between the maximum stresses under centre and third-point loading are 19.4 % for L/d = 2 and 3.4 % for L/d = 8.

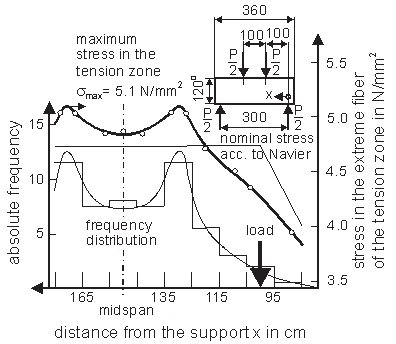Figure 1. The effective distribution of the extreme fibre stress in the tension zone at third-point loading calculated of the frequency distribution of the fracture origins of concrete specimens

Figure 2. Differences between the maximum stress in the extreme fibres of the tension zone and the nominal bending stress according to Navier[1] calculated by Naschold[5] using the stress distribution of Seewald[2]

A linear elastic behaviour cannot be assumed for bending tests on defect-free specimens of wood. The material is neither homogeneous nor isotropic. The load isnot introduced along a line, as supposed in the calculation of Seewald[2]. It is transferred via an area using bearing plates because of the low compression strength perpendicular to grain. Nevertheless, it should be stated that, especially for low values of L/d, the beam theory does not describe the stresses correctly.

Research on the stress distribution in wooden beams deals with the determination of shear stresses and stresses perpendicular to grain. Hooley and Hibbert[8] determined the longitudinal stresses in beams under two-point loading. The loads and support loads were assumed to be spread over a width of 0.1d. Small end cantilevers of a length of 0.2d were included. The loads were in a distance of 0.3 d from the supports. The values ofthe different elastic constants of Douglas fir in fibre direction and transverse to it were used. The contour lines for constant bending stresses (Fig. 5 in[8]) showed maximum longitudinal stresses, occurring in the extreme fibres of the tension zone between the load points. These maximum stresses were higher than 2.4 τ₀. The maximum stress results to 1.8 τ₀, according to the beam theory and the chosen loading configuration. τ₀ is the average shear stress between load and reaction. Therefore, the maximum stress acted at the expected location. It is more than 33 % higher than the one according to the beam theory.

Systematic differences in the bending strength can be obtained, depending on loading configuration and span-depth ratio, independent of the size effect.

3. Size Effect

It can be assumed, according to the theory of the size effect (weakest link theory), that the strength is dependent on the size of the highly stressed volume.

3.1. Tensile Strength

The tensile strength of defect-free specimens decreases strongly with increasing length of the specimens. Corresponding data of defect-free specimens can be found in the papers of Roš[9] (fir), Graf and Egner[10] (spruce), Rein[11] (pine heartwood and pine sapwood), Sumiya and Sugihara[12] (hinoki, lauan, and beech), Chudziński[13] (pine), Schneeweiß[14] (spruce), and Kunesh and Johnson [15] (Douglas fir, and hem fir). The data arepartly cited dependent on the area of the cross-section instead of the specimen length (Vorreiter[16] and Kunesh and Johnson [15]).

The maximum tensile stress in the extreme fibres of large beams was statistically below the tensile strength of small size standard specimens (Comben[17] and Malhotra and Bazan[18]). The difference became smaller as the size of the beam decreased. The uniaxial tensile strength is for specimens of the same volume lower than the extreme fibre tension stress of beams.

In regard to research on construction timbers see Glos and Burger[19], Burger and Glos[20], Steiger[21] and[22], Burger[23] (with literature overall view), and Takeda and Hashizume[24].

3.2. Compression Strength

Data on spruce of Schneeweiß[25] supplemented with data of the literature led to the following strength-volume dependence:

The compression strength decreases with increasing specimen volume, goes through a minimum, increases slightly to a maximum, and finally decreases again according to the size effect. Spruce showed the minimum at about 50 cm³ and the maximum at about 1000 cm³.

This volume dependence of the compression strength was also observed for concrete specimens (Schneeweiß[26]). It can be explained by the interaction between a size effect and a surface layer effect[25] and[26].

Steiger[22] examined spruce timbers with volumes of 864, 2048, 2560, and 8064 cm³. He found the maximum at 2048 cm³.

The values of tests of Okohira et al[27] showed on the average this wavy trend.

3.3. Bending Strength

The size effect of defect-free specimens was reduced to a depth effect by Tanaka[28], Monnin[29] and[30],Čižek[31], and Ylinen[32]. The weakest link theory was not mentioned.

Tests of Johnson[33], Talbot[34], Cline and Heim[35], Newlin and Trayer[36], and Schlyter and Winberg[37] deal mainly with the comparison of the bending strength of timber with the one of small specimens.

Sumiya and Sugihara[12] mentioned the weakest link theory of Epstein[38], who used the probability density function of Gauß for the strength values. The authors confirmed the linear regression between the strength and(log V)^1/2 according to this theory for tensile tests on lauan and hinoki and bending tests on beech (V = specimen volume).

Later on the extreme value distribution of type II of Fisher and Tippett[39] hasbeen used instead of the distribution of Gauß:Schneeweiß[40] to[42], Bohannan[43], Schneeweiß [44], Madsen and Buchanan[45], Madsen[46], and Madsen and Tomoi[47].

Bohannan[43] replaced in the weakest link theory the volume of the beams by the aspect ratio (product of length and depth). He concluded that the bending strength is independent of the width. Schneeweiß[44] found in tests on small clear specimens with varying width a maximum of the bending strength at about b/d = 4. An analysis of the bending strength of timbers (data of Chaplin and Nevard[48] and Thunell[49]) of different sizes showed a dependence of the size effect from the width[44]. Madsen[46] concluded from his data on defect-free Douglas fir that the volume effect is a more appropriate representation regarding the size effect than the aspect ratio.

Madsen and Buchanan[45] modified the theory to allow different magnitudes of size effects for length, depth, and width.

A synopsis of literature about the size effect of timber (and defect-free specimens) can be found in Denzler[50].

4. Criticism of the Weakest Link Theory

It should be mentioned that the weakest link theory can be used for chains[51] but, generally, not for specimens with different shapes and sizes[44]. A decrease of the size effect resulted[52] in tests on chains, if parallel connection occurs in addition to series connection. A stochastic process is used instead of the weakest link theory[14] and[53] in case of other materials, e.g. steel.

Equation (1) results from the weakest link theory using an extreme value distribution of type II with two parameters (2-parameter Weibull-distribution). f_m1 and f_m2 are the mean values of the bending strength. V₁ and V₂ are the volumes of the tested specimens. kis the formfactor of the distribution. Equation (2) with (1/k) = 0.87v can be used as an approximation of equation (1), with v as coefficient of variation[44].

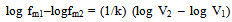(1)

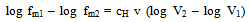(2)

The logarithm of the strength is linearly dependent on the logarithm of the specimen volume. This results in fact of the weakest link theory, but can also be deduced from experimental data[31]. Therefore, equation (2) was used by [44] for the consideration of the size effect, with the constants c_H and v determined experimentally.

Johnson[33] (white pine, shortleaf pine, longleaf pine, and oak) and Talbot[34] (longleaf pine, loblolly pine, and Douglas fir) performed tests of knot-free beams in bending. Graf and Egner[10] (spruce) used tensile specimens. Evaluations of these datain[44] resulted in c_H of 0.55 – 0.0062 u. u was the moisture content in % (between approximately 10 and 70 %).These c_H-values were clearly smaller than 0.87 and showed that the series connection cannot be used for specimens of different volumes. The length effect is expected to obey approximately the weakest link theory.

5. Flexural Fracture Curves (Theory)

The (theoretical) dependence of the bending strength from the span-depth ratio (flexural fracture curve) is obtained, as shown in Fig. 3[42] and[54]. Considered are: a) the distribution of the longitudinal stresses in a beam calculated by Seewald; b) the size effect; c) the transition fromflexural fracture to shear fracture. Not considered is that the deformation at the load points can diminish the bending strength, which is explained in detail later.

The size effect is reduced to a length effect regarding beams with constant cross-section and a pre-set loading configuration. Equation (1), therefore, can be written as:

(3)

The data follow principally the theoretical curve in the region of flexural fracture according to Fig. 3, if this correlation applies. The change of the stress distribution with the beam length and a possible transition to shear fracture arenot regarded in this equation.

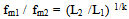Madsen and Tomoi[47] obtained for defect-free specimens 1/k = g = 0.20. Barrett et al.[55] stated for structural lumber of softwood1/k for the length effect (there named S_L) in bending S_Lb = 0.17, in tension S_Lt = 0.17, and in compression S_Lc = 0.10 (evaluation of test results of some authors). Equation (3) canonlybe used, if tests show dependences according to Fig. 3.

6. Flexural Fracture Curves (Tests)

Schneeweiß[42] carried out bending tests on simply supported beams of oak and spruce subjected to both, centre loading and third-point loading, to check the dependences according to Fig. 3.The cross-section of the specimens was kept constant for specimens within each of the series. The length of the specimens and, therefore, the span-depth ratio was changed.

Oak specimens (4 series) were loaded with the direction of load normal to the annual rings(horizontal annual rings). The angles between the direction of load and the annual rings were for spruce specimens (6 series)between 41 and 67°.

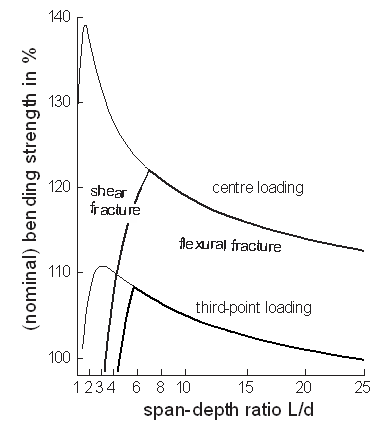Figure 3. The bending strength according to both, the size effect and the effect of the actual stress distribution (schematic)

Averaged data are shown in Fig. 4. They were fitted by curves, separated for specimens with shear fracture and for those with flexural fracture.

The bending strength curves of oak are in agreement with Fig. 3. The specimens tested under third-point loading showed lower bending strength values than those under centre loading, as expected from the size/stress effect. Furthermore, a larger span length leads to a lower bending strength in the region of flexural fracture independent of the loading configuration.

Tests on spruce led just under third-point loading to the dependence expected. Tests under centre loading showed an increase of the bending strength with increasing span length, contrary to Fig. 3. The test load at centre loading is transmitted by only one bearing plate, but at third-point loading by two bearing plates (all plates with the same dimensions). The pressure under the bearing plate is in case of centre loading for large span length slow. The specimens show in agreement with the size/stress effect still higher strength than the ones tested under third-point loading. Higher loads are necessary for fracture, when reducing the span length. Therefore, also the pressure under the bearing plates increases. The deformation under the bearing plates at centre load was larger than under the two bearing plates in case of third-point loading. This finally resulted in a bending strength under centre loading below the one under third-point loading.

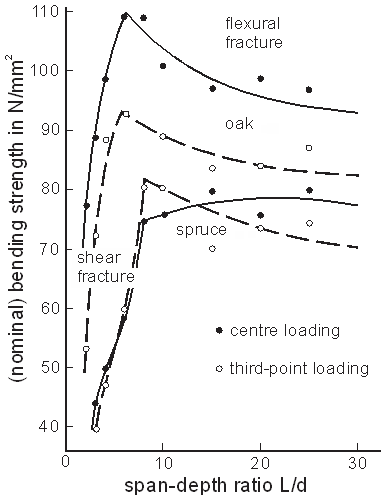Figure 4. Differences in the shape of the fitting curves of the bending strength of wood with high (oak) and low values (spruce) of the compression strength perpendicular to grain

The expected transition from flexural to shear fracture occurred for both tested wood species.

The increase of the bending strength with increasing span length has not been considered up to now nor exist papers dealing with the size effect according to the weakest link theory. This increase will be discussed later.

7. Bending Strength and Span Length

7.1. Tests of Baumann

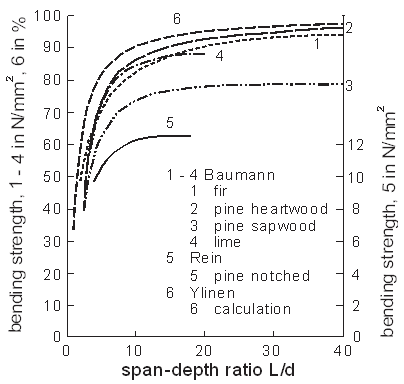
Two different length effects can be expected for small clear specimens according to Fig. 4. These are increasing or decreasing of the bending strength increasing span length. Examples for the increasing strength are the well-known data for centre loading of Baumann[56] for the following species of wood:fir, pine heartwood, pine sapwood, and lime.

Data exist for the three species of wood mentioned before, both for the direction of the load normal to the annual rings(horizontal annual rings) and for the direction of the load parallel to the annual rings (vertical annual rings)in dependence of L/d.

Baumann[56] did not distinguish between shear fracture and flexural fracture. The average bending strength values of both annual ring orientations were fitted by a curve, increasing continuously with increasing span length. These fitting curves, according to equation (4) (designations of Baumann), are shown in Fig. 5. The equation is based on the assumption that at span-depth ratios above L/d = 40 no further increase of the bending strength occurs:

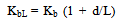(4)

Where in K_bL is the bending strength of a long beam (which means for one with L/d ≥ 40), and K_b is the bending strength of the short beam regarded.

It should be mentioned that these fitting curves were multiply reproduced in literature[16],[57], and[58].

Baumann[56] published further data with regard to the length effect using centre loading. Theannual ring orientations were not indicated for these tests. A comparison of the bending strength of tenshort beams of pinewood with L/d = 7.0 to 9.0 with the bending strength often long beams with L/d = 25.9 to 33.3 resulted in a ratio of 0.84:1. Smaller differences were found in further tests with beams of pine, ash, and birch. These data show, therefore, the same trend as the data in Fig. 5.

Figure 5. Examples of increasing bending strength with increasing beam length

7.2. Further Tests from Literature

Ylinen[59] calculated the length effect for simply supported beams. The load was distributed uniformly in the middle of the span over a range c (length of the bearing plate at the load point). The calculation of Ylinen was performed without consideration of the size effect and the possibility of shear fracture. The curves are determined for beams with rectangular cross-section and straight horizontal annual rings with distinct differences of the properties of earlywood and latewood. Ylinen received, as Baumann, contrary to the calculation of Seewald, curves increasing steadily with L/d. In both calculations the curves approach to a limit value. The equation, obtained by Ylinen, agrees with equation (4) of Baumann under special assumptions.

Rein[11] found the same length effect as Baumann[56] for beams of pine with a notch at mid-span. The calculated curves of Ylinen [59] and the fitted curve of Rein[11] are shown in Fig. 5.

Tests of Bechtel and Norris[60]on Sitka spruce resulted in an increase of the bending strength, as well under centre loading, as also under two-point loading, with an increase of the span-depth ratios from L/d = 10 to L/d = 14. The increase was smaller in tests with two-point loading than for centre loading.

Chudziński[13] tested beams with different length, resulting in higher bending strength values for longer beams.

Bohannan[43] analysed the length effect of beams of Douglasfir. 343 and 210 beams were tested with centre loading at span lengths of 36 and 46mm and led to average bending strength values of 91.4 and 92.1 N/mm².

Most of the time a decrease of the bending strength with increasing span length was established in construction wood. This is according to Madsen and Buchanan[45] valid, independent of the loading configuration (centre loading, two-point loading, and third-point loading).

8. Centre –and Third-Point Loading

8.1. Tests on Defect-Free Specimens

A higher bending strength is expected in tests under centre loading than under third-point loading, caused by the size/stress effect.

The ratio of the values of the considered characteristics, determined for beams under centre loading and under third-point (or two-point) loading, is called R_CT. Bohannan[43] calculated R_CT according to the size effect

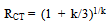(5)

The coefficient of variation in bending tests is usually around v = 0.16. This value results, using 1/k = 0.87 v, in k = 7.18 and according to equation (5) in R_CT = 1.19. This value increases a little, considering the actual stress effect.

The bending strength under centre loading is diminished by deformations at the load point, if the ratio R_CT of the measured bending strength values is considerable lower than R_CT = 1.19.

R_CT< 1 means that the bending strength under centre loading is even lower than under third-point loading.

Kühne et al.[61] used beams with a span length of 900 mm and L/d = 18. The two-point loaded beams had a load point distance of 500 mm. The authors obtained different values of R_CTin test series on specimens of spruce, fir, larch, beech, and oak. They were always higher than R_CT = 1, independent of density and moisture content.

Madsen[46] tested defect-free Douglas fir beams with a depth of 25 mm and span lengths of 360 and 720 mm (L/d = 14.4 and 28.8). The moisture content of dry material was 12 %, for wet material it was above the fibre saturation point. Madsen found for the dry material R_CT = 1.17 (L/d = 14.4) and R_CT = 1.30 (L/d = 28.8) and for the wet material R_CT = 1.03 and R_CT = 1.06.

Malhotra and Bazan[18] conducted tests on knot-free beams of eastern spruce (d = 42 to 287 mm) and Douglas fir (d = 42 and 140 mm), with span-depth ratios of L/d ≈ 16. The ratios of the bending stresses at the proportional limit were for spruce R_CT = 1.10 to 0.92. Higher beams yielded to lower values of R_CT. The ultimate bending moments led without a trend to R_CTvalues between 0.92 and 1.05. The corresponding average values of the two characteristics (proportional limit and ultimate bending moments) were for Douglas fir R_CT = 1.14 and 1.16.

Bechtel and Norris[60] performed bending tests on clear and straight grained beams of Sitka spruce with a depth of 5 mm using centre loading and two-point loading with a load point distance of 15 mm. They obtained flexural fractures for L/d = 10 and L/d = 14 with R_CTvalues of 0.83 and 0.91, respectively.

The value R_CT can be higher or lower than 1. It increases in both cases with increasing span-depth ratio(Madsen[46]), if the bending strength is reduced by the deformation at the load point.

Schneeweiß[42] performed tests on oak and spruce with constant span length, additionally to the ones with different span length.

8.1.1. Tests on Oak

The width of the specimen was 20 mm, the depth 40mm, the span length 320mm forcentre load in gand 480mm for third-point loading. The span length was chosen in a way that the shear length wasthe same in both specimen types. 12 beams were cut out of the tested plank next to each other. Theannual rings were partly normal to the loading direction (beams out of the middle of the plank), partly they ran from edge to edge (beams out of the edge of the plank) of the cross-section. Each beam was cut into three specimens, which were taken for both loading configurations, alternately lying behind each other. The average bending strength resulted for third-point loading in 95.6 N/mm², for centre loading in113.9 N/mm² corresponding to R_CT = 1.19.

8.1.2. Tests on Spruce

Four beams with a quadratic cross-section with an edge length of 35 mm were cut out of a plank next to each other. Seven specimens were taken of the beams lying behind each other. They were tested with a span length of 300mm under centre loading, with one of 340mm under two symmetrically placed loads in a distance of 40mm, and with one of 450mm under third-point loading. The shear length was the same for the three types of tests. The average bending strength in the tests was 76.5 N/mm² for two-point loading and 76.1 N/mm² for third-point loading.The bending strength was a little higher under two-point loading than under third-point loading according to the length effect. The highest bending strength should result under centre loading. Actually, the lowest value of 59.2 N/mm² was obtained and resulted in R_CT = 0.78. An indentation of the bearing plates into the wood could be found. This was also shown by the average remaining indentation depth of 0.95 mm for third-point loading and 1.70 mm for centre loading.

8.2. Tests on Construction Wood

The data were approximately according to the size/stress effect for timber beams, which means, the bending strength was higher in tests under centre loading than under third-point loading: Bohannan[43], Madsen and Nielsen[62], Madsen and Buchanan[45], Ehlbeck and Colling[63], Kessel [64], Madsen[65], and Denzler[50].

Madsen[65], for example, stated in a table the ratio of the bending strength centre loading/third-point loading to R_CT = 1.22.

9. Bending Strength and Annual Ring Orientation

9.1. General Notes

Duhamel du Monceau[66] was the first, who stated that beams placed with vertical annual rings are carrying more load than beams with horizontal annual rings. Later on, this problem was discussed by Nördlinger[67], Wijkander[68], and Rudeloff[69].

The specimens shall be, according to ASTM D 143-2003, placed that the load acts through the bearing block to the tangential surface near the pith. Tests on vertical annual rings are intended in other standards.

In the following, some factors influencing the measured bending strength are summarized.

9.2. Horizontal Rings, Pith near the Compression or Tension Side

Bending tests on beams with horizontal annual rings can be performed that the wood next to the pith can be arranged in the tension or compression zone. As an example, bending tests of Tetmajer[70] on pine, spruce, white fir, and larch, with bending in the direction away from the pith (near the compression side), resulted in lower bending strength values than in the opposite direction. The result in oak was changing. In beach the opposite resulted.

9.3. Annual Ring Width

Grotta et al.[71] found in test on Douglas fir beams that vertical rings give higher bending strength, up to an annual ring width of 3.6 mm, and higher or lower strength values (both cases occurred) above this annual ring width.

9.4. Moisture Content

Markwarth and Wilson[72] examined beams of Sitka spruce and Douglas fir in the green and air-dried or kiln-dried condition. Both species of wood showed in the green condition a higher bending strength with vertical rings. This was also true for the kiln-dried Douglas fir, but not for the air-dried Sitka spruce, where the difference was negligible (58.3 and 58.4 N/mm²).

9.5. Position of Earlywood or Latewood

Grotta et al.[71] tested defect-free specimens of small dimensions with horizontal annual rings. It was found to be important, whether the surface fibres in the compression or tension zone were of earlywood or of latewood. Forsaith[73] researched this problem in detail.

9.6. DataTaken from Literature

9.6.1. Softwood

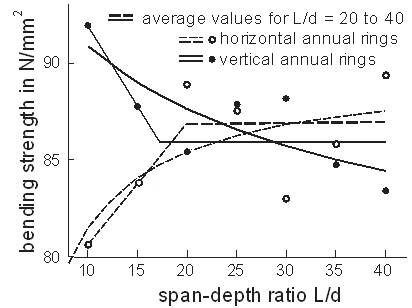
The published data of Baumann[56] in Fig. 6 for fir, pine heartwood, and pine sapwood were averaged separately for each of the two annual ring orientations. It was assumed that for L/d ≥ 8 only flexural fractures occur. The data for smaller span-depth ratios are not shown.

Figure 6. Average values of the bending strength for the two annual ring orientations using data of Baumann on fir, pine heartwood, and pine sapwood, evaluated by two different versions (curves according to equations (3) and (4))

It is obvious to use a power law according to equation (3) for the decreasing curve, obtained for the vertical rings, and equation (4) for the increasing curve, obtained for the horizontal rings,in a regression analysis of the data. The two curves are drawn in Fig. 6. They have a crossing point at L/d = 26. It is to notice that at large span-depth ratios horizontal rings led to higher bending strength than vertical ones.

Another way to interpret the data is also shown in Fig. 6. The data for L/d ≥ 20 were averaged. The average bending strengths of 86.8 N/mm² for horizontal annual rings and 85.9 N/mm² for vertical annual rings were drawn as horizontal lines.The average bending strengths for L/d ≥ 20 were in this evaluation only a little higher for horizontal than for vertical annual rings. Straight lines were drawn through the data for L/d = 10 and L/d = 15 up to the horizontal lines and resulted in two salient points at L/d = 17 and L/d = 20, respectively.

Both evaluations led to the conclusion that at the standard span-depth ratio L/d = 15 the bending strength was influenced by the deformation at the load point.

However, it has to be considered that the locations of the salient points in Fig. 6 are dependent on the testing conditions and, especially, on the behaviour of the wood in compression perpendicular to grain.

Therefore, it cannot be assumed, generally, that tests with span-depth ratios of L/d = 14 or 15 on softwood with vertical annual ringslead to higher bending strength values than for such with horizontal annual rings.

The bending strength versus the span-depth ratio is shown in the paper of Baumann[56] for a wide range of the span length. Data could be found in other papers for both annual ring orientations, most of the time only for one span length. Such data are shown in table 1, where the keywords vertical or horizontal point out the corresponding annual ring orientation, resultingin higher bending strength values.

Table 1. Effect of the ring orientation on the bending strength of softwood: authors, who measured higher strength values at horizontal or vertical annual rings:1) Vertical annual rings led to higher strength values.2) Horizontal annual rings led to higher strength values

9.6.2. Hardwood

The dependence of the bending strength over a widerange of the span-depth ratio was determined by Baumann[56]for lime and by Schneeweiß[42] for oak, but not for both annual ring orientations. Data could be found in references for softwood and hardwood for both annual ring orientationsbut onlyfor one span length, see table 2.

Table 2. Effect of the ring orientation on the bending strength of hardwood: authors, who measured higher strength values at horizontal or vertical annual rings:1) Vertical annual rings led to higher strength values.2) Horizontal annual rings led to higher strength values

10. CompressionStrength Perpendicular to Grain

10.1. General Notes

The behaviour of specimens under compression perpendicular to grain can be defined by different characteristics (stress at the proportional limit, maximum stress, and stress corresponding to a certain offset or total strain (Gehri[80])). In the following it is just established, if the value of the examined characteristic has been higher or lower for radial (load direction normal to the annual rings) or tangential compression (load direction tangential to the annual rings). The term strength is used independent of the characteristic determined.

10.2. Softwood

Softwood (and ring porous hardwood) has a distinct alternation of lower density earlywood and higher density latewood. The dense latewood layers have to support the major part of the loadin tangential compression. The latewood layers fail,according to Bodig[81], like long columns or plates, and are the controlling factors. The participation of the earlywood layers in the support of the load is, because of low strength, not as important as the lateral support of the latewood layers.

The first failure is in radial compression, located in the weakest earlywood layer (additional failures occur in the same or in several other earlywood layers, as the compression progresses). Latewood layers act as load distributors. A low ray volume is typical for softwood. The strength in radial compression is determined only by earlywood, while in tangential compression latewood is the controlling factor.

10.3. Hardwood

Hardwood has higher ray volumes than softwood. Rays have a supporting effect in radial direction (Huber and Prütz[82], Rothmund[83] and[84], Bodig[81], and Kennedy [85]). The effect of latewood, raising the strength in tangential compression, was already mentioned. Therefore, the ratio between the strength of radially and tangentially loaded specimens increases with higher ray volume and decreases with the latewood percentage (Kennedy[85]). Ring porous hardwood has partly higher volumes of latewood, diffuse porous hardwood in generally lower ones (Kennedy[85]). Therefore, the radial strength of diffuse porous hardwood is obviously higher than the tangential one, but for ring porous hardwood the differences may be small (Kollmann[57]).

10.4. Factors Influencing the Measured Strength Values

10.4.1. Definition of the Compression Strength Perpendicular to Grain

The choice of the definition of the compression strength can cause different assessments (Bodig[81] and Ellis and Steiner[86]), if the stress-strain curves for the two annual ring orientations intersect.

10.4.2. Density

Different densities can cause different test results for the same species of softwood. Rothmund[83] and[84] received for high density spruce and pine specimens higher strength values in tangential than in radial and for specimens with low density higher strength values in radial than in tangential compression. The specimens of oak were stronger in radial than in tangential compression, independent of their density.

10.4.3. Ring Curvature

The curvature of the annual rings can influence the strength of the specimens according to Madsen et al.[87], especially, in tangential compression.

10.4.4. Height

The latewood layers buckle in specimens with vertical annual rings easier, the greater the specimens’ height (Staudacher[88]). The influence of the height of the specimens is in radial compression significantly lower than in tangential one (Gaber[89] and Rothmund[83]). Small specimenheights, therefore, advantage higher strength in radial compression.

So, different authors can find different results concerning the strength of specimens with vertical or horizontal annual rings of the same species.

10.5. Results of a Literature Research

10.5.1. Softwood

Some authors (Vorreiter[16], Kollmann[57], Bodig[81], Perelygin[90], Kennedy[85], and Mönck and Rug[91]) stated that softwood shows a higher strength perpendicular to grain in tangential compression (vertical annual rings) than in radial one (horizontal annual rings).

Exceptions arise, see table 3, from low densities, as for instance in case of western red cedar (0.322 g/cm³, Kennedy[85] or 0.323 g/cm³, Ellis and Steiner[86]),sugar pine (0.276 g/cm³, Kennedy[85]), low density pine (0.39 g/cm³, Rothmund[83] and[84]), low density spruce (0.33 g/cm³, Rothmund[83] and[84]). Low density is correlated with low latewood percentage (sugar pine 3.4 %, Kennedy[85] and western red cedar 15 %, Kennedy[85]).

The data of Frey-Wyßling and Stüßi[92] may be influenced by the large specimens’ height of 75 mm, which promote higher strength in radial compression.

Table 3. Effect of the ring orientation on the compression strength perpendicular to grain of softwood: authors, who measured higher strength values at horizontal or vertical annual rings:1) Vertical annual rings led to higher strength values.2) Horizontal annual rings led to higher strength values

10.5.2. Hardwood

Some authors mention that specimens of hardwood in radial compression shall generally show higher strength values: Vorreiter[16] and Mönck and Rug[91]. Table 4 gives the results of the literature search. Data of Casati[74] on small hardwood cubes show, probably due to the small height of 20 mm, higher strength values in tangential than in radial compression for the wood species alder, elm, poplar, and white poplar. These findings are not confirmed by other authors and not included in table 4.

Table 4. Effect of the ring orientation on the compression strength perpendicular to grain of hardwood: authors, who measured higher strength values at horizontal or vertical annual rings:1) Vertical annual rings led to higher strength values.2) Horizontal annual rings led to higher strength values

11. Bending Strength and Compression Strength Perpendicular to Grain

It can be seen that in general both, the bending strength and the compression strength perpendicular to grain, in case of softwood are higher for vertical annual rings and in case of hardwood higher for horizontal annual rings. There are some exceptions, but also in these cases conformity can be seen. Spruce and Douglas fir show changing results in both types of tests. Ash, as a ring porous hardwood, results in both types of tests into higher values for vertical annual rings, contrary to the statements before. All this confirms the opinion that the compression strength perpendicular to grain influences the bending strength.

In the following some facts are given, which support this opinion:

Data on oak with vertical annual rings show according to Fig. 4a nearly unnoticeable influence on the strength perpendicular to grain, because for oak this one is very largefor horizontal annual rings(16.7 N/mm²) as well as for vertical ones (11.6 N/mm²)(Baumann[56]).

Fig. 6 shows in the range of L/d = 8 to L/d = 20 that the average bending strength for three tested species of wood, these are fir, pine heartwood, and pine sapwood, increased with increasing span-depth ratio for horizontal annual rings and decreased for ones. Additionally, it should be mentioned that this tendency also appliesseparately for all three species of wood.

The compression strength perpendicular to grain for horizontal annual rings were stated in Baumann[56] for these three species of wood with 3.6, 5.5, and4.7 N/mm², for vertical annual rings on the other hand with 7.6, 8.6, and 9.4 N/mm².Therefore, the lower strength values for horizontal annual rings were responsible for the decrease of the bending strength with decreasing beam length.

12. Summary, Conclusions

A decrease of the bending strength could be expected with increasing span length caused by size effects. Furthermore, the bending strength under centre loading should be higher than under third-point loading.

The weakest link theory leads, using the two-parameter Weibull distribution, to a straight line in a diagram log (bending strength) versus log (span length). The slope of the fitting straight line has to be determined by the coefficient of variation of the individual values, if the measured values are expected to obey this theory. In general, this connection was not checked in literature.

The actual occurring maximum bending stressin the tension region depends on the span length and is lower for centre loading and higher for third-point loading, than stated in the beam theory. This effect overlaps the size effect to a size/stress effect, which means, the slope of the straight line mentioned decreases more under centre loading(for L/d > 2) and less under third-point loading than according to the weakest link theory. There are larger differences of the bending strength between centre and third-point loading in case of a smaller span length. Altogether, the size effect prevailed.

A fundamental change of this trend results, if the bending strength is diminished caused by the deformation under the bearing plates.

The assumed size/stress effect could be found in tests on oak as well for centre as also for third-point loading. The tests on beams of spruce resulted for third-point loading in the expected shape of the curves. The bending strength decreased in tests under centre loading with decreasing span length and sank even below the one tested under third-point loading. It is to notice that under third-point loading the load was transferred by two bearing plates and under centre loading only by one with the same dimensions. The compression strength perpendicular to grain is higher for oak than for spruce.

Literature research and own evaluations showthat especially the values of the bending strength under centre loading can decrease with decreasing span length, contrary to the weakest link theory.

Generally, the compression strength perpendicular to grain is higher or lower for those annual ring orientations, in which the bending strength of the wood types tested was also higher or lower.All these test results could be explained by a deformation under the bearing plates.

Summarizing, the simple weakest link theory cannot be used directly, because bending specimens do not meet the requirements of this theory as chains do. Furthermore, this theory does not consider the actual stress distribution in a beam under bending (an accommodation is possible), and the deformation at the load points diminishes more or less the bending strength.

It may be possible to use the fundamental relations of the theory, but just if the coefficients are determined by tests.