-
Paper Information
- Previous Paper
- Paper Submission
-
Journal Information
- About This Journal
- Editorial Board
- Current Issue
- Archive
- Author Guidelines
- Contact Us
American Journal of Materials Science
p-ISSN: 2162-9382 e-ISSN: 2162-8424
2012; 2(2): 34-38
doi: 10.5923/j.materials.20120202.07
Determination of Exact Steady State Creep Behavior in Short Fiber Composites by Mapping Transformation Function (MTF) in MMC’s
Vahid Monfared
Department of Mechanical Engineering, Zanjan Branch, Islamic Azad University, Zanjan, Iran
Correspondence to: Vahid Monfared , Department of Mechanical Engineering, Zanjan Branch, Islamic Azad University, Zanjan, Iran.
| Email: |  |
Copyright © 2012 Scientific & Academic Publishing. All Rights Reserved.
A novel mathematical model based on mapping function is presented for determination of exact steady state creep behaviour in short fiber metal matrix composites 6061Al/15%SiC (MMC’s) subjected to axial loading. FEM and analytical steady state Creep behaviour of 6061Al/15%SiC (MMC’s) composites wasn’t coinciding to the previous experimental results in Prior researches. In this paper, transformation function is introduced in order to convert previous analytical and FEM results to experimental results correctly. Mapping function method (MFM) is exact approach for transformation of analytical and FEM results to experimental results in MMC’s. Also, fiber behaviour is elastic unlike creep behaviour of matrix. In addition mapping transformation function is introduced analytically. Eventually, good agreement is established between the results of new mapping function method (MFM) and previous experimental results for prediction of steady state creep behaviour in short fiber composites (SFC’s).
Keywords: Composites, Creep, Analytical and FEM Results, MMC, SFC, Mapping Function
1. Introduction
- Short fiber composites (SFC), are growing in eminence in aircraft and aerospace industry, automotive and commercial business machine applications. They present the advantage of weight reduction, design flexibility, energy savings, and high volume processes for appearance and structural applications. In order to determine the maximum advantages from short fiber composites (SFC’s), increasing amounts of researches and development activities have been initiated at many universities and research – laboratory centers. In addition, Short fiber reinforced polymers, metals and ceramics (PMC, MMC, CMC) were developed eminence to fill the property gap between continuous fiber laminates used as structures by the aircraft and aerospace industry and other applications.Many researchers have investigated the steady state creep behaviour by analytical and experimental methods. Most of them have studied steady state creep problems by analytical, experimental and finite element method (FEM) without reformation of analytical results to experimental results. Of course, some their results were similar to the experimental and finite element methods well. Result of the new polynomial mapping functions for determination of creep strain rate is very exact and wonderful. Creep is more serious in materials that are subjected to high temperatures and loads for long periods, and close to melting point. The increasing application of short fiber composites in high loadings and temperatures environments requires a thorough knowledge of their creep characteristics and deformation mechanisms. Recently, extensive investigations have been performed to obtain the creep behaviour of short fiber composites in steady state creep[1–6]. Also, in the present new work, an analytical and mathematical solution for prediction of the steady state creep behaviour of short fiber composites based on mapping transformation polynomial function is determined without using of some theories. For example, this method (MTF) can be used for analysis of second stage creep in nano short fiber composites, rupture time and mechanical design based on creep. One of applications of Strong MTF’s approach is its ability in analysis of all nano-composites creep, because of high performance in expansion of boundary conditions. Note that, contact surface in nano composites and interface boundary conditions are very extensive. Therefore, MTF due to high performance is unique and perfect method that can analyse nano-composites creep. In addition, mentioned method can analysis creep behaviour of short fiber composites in different region of unit cell analytically. Here, an axisymmetric unit cell representing a fiber with its surrounding matrix as two coaxial cylinders is assumed. For verification of the solution method, the SiC/6061Al composite is selected as a case study and the results will be compared with the previous experimental available results in[5]. New mathematical formulation based on mapping transformation function is introduced for determination of exact second stage creep behaviour in short fiber metal matrix composites 6061Al/15%SiC (MMC’s) under axial loading. Analytical steady state Creep behaviour of 6061Al/15%SiC (MMC’s) composites wasn’t similar to the prior experimental results in earlier researches. In this research, transformation function is developed for converting of previous analytical and FEM results to experimental results exactly. Mapping function method (MFM) is precise, meticulous and extremely accurate approach for conversion of analytical and FEM results to experimental results in MMC’s. In addition mapping transformation function is presented analytically. Finally, good concurrence is found between the results of new mapping function method (MFM) and prior experimental results for prediction of steady state creep behaviour in short fiber composites (SFC’s). Mondali et al.[1] proposed new analytical shear-lag based model for prediction of the steady state creep deformations of some short fiber composites by Imaginary fiber technique. Boubakri et al. investigated influence of thermal aging on tensile and creep behaviour of thermoplastic polyurethane[2]. Creep of fibrous composite materials has been studied by Lilholt[3]. FEM study of the second stage creep behaviour of Al6061/SiC metal matrix composite has been studied by Mondali et al.[4]. Morimoto et al.[5] investigated second stage creep of silicon carbide whisker/6061 aluminum composite at 573 K. Ghavami et al. presented finite difference solution of steady state creep deformations in a short fiber composite in presence of fiber/matrix debonding[6]. Monfared[7] proposed new analytical formulation for contact stress and prediction of crack propagation path in rolling bodies and comparing with finite element model (FEM) results statically. Prediction of Mechanical Behaviour of PZT and SMA has been studied by Monfared and Khalili[8]. Cibulka presented constrained open mapping theorem with applications[9]. Fernandez and Gonzalez-Doncel[10] determined threshold stress and load partitioning during creep of metal matrix composites. Boniecki, et al.[11] studied . Steady state creep of a composite with short fibres was investigated by Mileiko[12]. Fukuda and Chou proposed advanced shear-lag model applicable to discontinuous fiber composites[13]. Xu et al.[14] investigated . Nedjar presented[15]. Nieh[16] studied creep rupture of a silicon-carbide reinforced aluminum composite. Creep deformation of metal–matrix composites have been investigated by McLean[17]. was investigated by Kouadri-Boudjelthia et al.[18]. Pachalis et al.[19] presented modelling of creep of aligned short-fiber reinforced ceramic composites. Wang and Chou proposed analytical modelling of creep of short fiber reinforced ceramic matrix composite [20]. The elasticity and strength of paper and other fibrous materials has been investigated by Cox[21]. Interfacial debonding and fiber pull-out stresses of fiber-reinforced composites have been studied by Hsueh[22]. Interfacial debonding and fiber pullout stresses of fiber-reinforced composites Part VII: Improved analysis for bonded interfaces was investigated by Hsueh[23].A modified analysis for stress transfer in fiber-reinforced composites with bonded fiber ends was proposed by Hsueh [24]. Hsueh and Becher studied residual thermal stresses in ceramic composites[25]. Hsueh et al.[26] investigated stress transfer in a model composite containing a single embedded fiber. Boyle and Spence proposed stress analysis for creep [27]. Gao and Li[28] presented shear-lag for carbon nanotube-reinforced polymer composites. Jiang et al.[29] presented analytical model for elastic stress field distribution in fibre composite with partially debonded interface. Lee et al. [30] proposed . Sometimes, theoretical predictions differ from the experimental data in fibrous composites because of some reasons such as debonding, material and manufacturing defects and etc. Therefore analytical prediction is very important for analysing creep behaviour of fibrous composites.
2. Material and Methods
- First, creep strain rate relations with respect to applied loads are presented in polynomial functions. The cylindrical unit cell depicted in Figures 1, 2 has been used to model a short fiber composite.
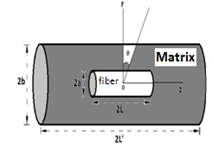 | Figure 1. Presentation of the unit cell schematically |
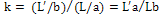 is considered as a parameter related to the geometry of the unit cell. An applied axial stress
is considered as a parameter related to the geometry of the unit cell. An applied axial stress 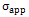 is evenly induced on the end faces of the unit cell (at z =
is evenly induced on the end faces of the unit cell (at z =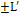 Steady state condition of stress is assumed and a full and perfect fiber-matrix interface is considered. Elastic deformations are very small and are neglected as compared to creep deformations. The fibers have elastic behaviour during the analysis and the Steady state creep behaviour of the matrix, which its properties are considered to be constant with temperature, is described by an exponential law as given in Equation 1.[27],
Steady state condition of stress is assumed and a full and perfect fiber-matrix interface is considered. Elastic deformations are very small and are neglected as compared to creep deformations. The fibers have elastic behaviour during the analysis and the Steady state creep behaviour of the matrix, which its properties are considered to be constant with temperature, is described by an exponential law as given in Equation 1.[27],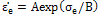 | (1) |
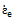 and
and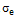 are the equivalent stress and equivalent strain rate of the matrix respectively, will be functions of r and z coordinates. Thus, it turns out to be a very complex nonlinear problem.For validation and verification of the solution method, the SiC/6061Al composite is selected as a case study and the results will be compared with the previous experimental and analytical results. For the composite used here (SiC/Al6061), the volume fraction (f) of fibers is 15% and the fibers have an aspect ratio (s) of 7.4 and k = 0.76[5].
are the equivalent stress and equivalent strain rate of the matrix respectively, will be functions of r and z coordinates. Thus, it turns out to be a very complex nonlinear problem.For validation and verification of the solution method, the SiC/6061Al composite is selected as a case study and the results will be compared with the previous experimental and analytical results. For the composite used here (SiC/Al6061), the volume fraction (f) of fibers is 15% and the fibers have an aspect ratio (s) of 7.4 and k = 0.76[5].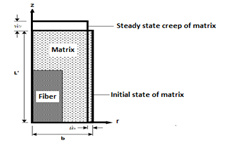 | Figure 2. Schematic of the unit cell edges in the 2nd stage creep and the elastic states |
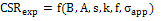 | (2) |
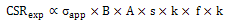 | (3) |
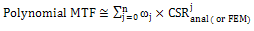 | (4) |
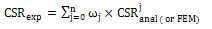 | (5) |
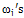 are determined by analytical, finite element analysis (FEA) and experimental results, these results given as, k=1 In above formulations, exp and anal indices indicate experimental and analytical. For example if n=2, given as
are determined by analytical, finite element analysis (FEA) and experimental results, these results given as, k=1 In above formulations, exp and anal indices indicate experimental and analytical. For example if n=2, given as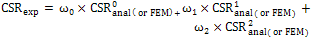 | (6) |
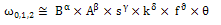 | (7) |
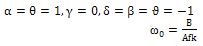 | (8) |
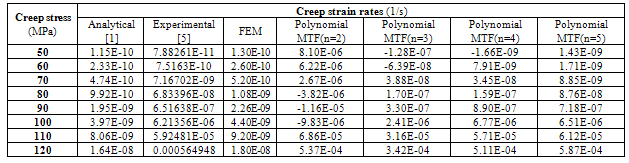
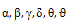 are determined by analytical, finite element analysis (FEA) and experimental results. Also, A, B are material properties in steady state creep in MMC’s. Also, creep strain rate (1/s) versus creep stress (MPa) is obtained without using of some complex and intricate theories. Creep strain rate respect to creep stress has been determined by prior researchers in various and difficult methods. This new approach is very easy, uncomplicated and direct. Thus,
are determined by analytical, finite element analysis (FEA) and experimental results. Also, A, B are material properties in steady state creep in MMC’s. Also, creep strain rate (1/s) versus creep stress (MPa) is obtained without using of some complex and intricate theories. Creep strain rate respect to creep stress has been determined by prior researchers in various and difficult methods. This new approach is very easy, uncomplicated and direct. Thus,  is obtained for n=5, 4 respectively by Equation 9.
is obtained for n=5, 4 respectively by Equation 9.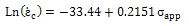 | (9) |
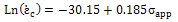 | (10) |
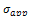 is applied tensile load.
is applied tensile load.3. Results and Discussion
- Polynomial mapping functions should be analysed for presentation of mapping transformation function (MTF). This analysis shows that polynomial mapping functions in order 5 (n=5) are very exact for accurate determination of experimental results. That is, polynomial mapping functions map the previous analytical and FEM results into experimental results exactly. All of the previous analytical results transform to prior experimental results correctly. These discussions have been shown in Figures 3, 4 and Table 1.
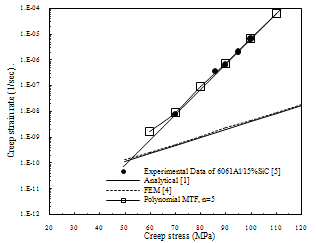 | Figure 3. Effect of polynomial mapping transformation function (Polynomial MTF) on analytical[1] and FEM results for a 6061Al/15%SiC steady state creep at 573 K ,n=5 (Tensile load) |
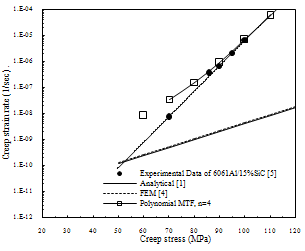 | Figure 4. Effect of polynomial mapping transformation function (Polynomial MTF) on analytical[1] and FEM results for a 6061Al/15%SiC steady state creep at 573 K ,n=4 (Tensile load) |
|
4. Conclusions
- Analytical formulation based on mapping function was developed for determination of exact steady state creep behaviour in short fiber metal matrix composites 6061Al/ 15%SiC (MMC’s) under axial tensile load. FEM and analytical steady state Creep behaviour of 6061Al/15%SiC (MMC’s) composites wasn’t similar to the previous experimental results in Prior researches. Therefore, transformation function was presented in order to convert previous analytical and FEM results to experimental results correctly.Mapping function method (MFM) is exact approach for transformation of analytical and FEM results to experimental results in MMC’s. Hence, mapping transformation function was introduced analytically. Eventually, good agreement was established between the results of new mapping function method (MFM) and previous experimental results for prediction of steady state creep behaviour in short fiber composites (SFC’s). Polynomial mapping functions with different exponent were compared for exact determination of mapping transformation function (MTF). These comparisons shown that well-behaved polynomial mapping function with n=5 is more accurate than the other forms for determination of experimental results. That is, polynomial mapping functions mapped the previous analytical results into experimental results precisely. All of the previous analytical results were transformed to its experimental results by mapping transformation function (MTF) correctly.
 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-Text HTML
Full-Text HTML