1. Introduction

Polymeric materials, which for a long time have been considered as classical insulators, receive now increasingly more applications in polymer electronics at creation of flexible film batteries, anisotropic conductive films (ACF), for technology of printed circuit boards, large-scale display screens, etc.[1]. Though the progress of this researches area is connected first of all with the discovery of conductive doped conjugated polymers (the Nobel Prize in chemistry 2000), for which there is a well-developed theory[2,3], now the possibilities of wide-band-gap non-conjugated polymers (WBP) are actively investigated also. For this polymers relatively high value of conductivity can be achieved either by creating a composite, i.e. introduction in the insulating polymer matrix of conducive inclusions (e.g., metallic nanoparticles, which has also demonstrated electrical bistability and memory effect, used for creation of non-volatile memory devices[4]), or by use of extremely thin, from nanometers up to sub-micron films, for which various fairly weak external influences (electric or magnetic field, pressure, etc.) can result in transitions to highly conductive state (HCS)[5].

Methodically one should separate a "purely thin-film" size effects, which include relatively high field strength, the dominance of processes of charge injection from electrodes and tunneling through a thin insulator layer, and the physi-cal processes associated with actual bulk conductivity of WBP in weak fields. Thus, a widespread special reduction MOM for Metal - Organic – Metal structures, in fact, stresses that for organic thin film between two metal electrodes molecular structure of this film often does not play an essential role in study of electrical conductivity, and so it is not connected, for example, with the bulk conductivity of polymers. Indeed, though in the study of thin-film MOM for various organic substances, including polymers, there are reliable experimental data, which are quantitatively consistent with some existing theoretical models, the general understanding of physical mechanisms that explain the totality of observed phenomena is now actually absent[5]. It is also clear that to study anomalies of the actual conductivity of WBP it would be correct restrict as far as possible the influence of electrodes and "thin film" size effects.

For thin films in HCS the WBP conductivity is radically different from the conductivity of metals and other spatially homogeneous conducting systems primarily due to the presence of strong spatial inhomogeneity, often leading to appearance of filamentary structure with nano-sized current-carrying channels[6] (as estimated from experiments[7], the transverse dimensions of these channels are less than 100 nm). This specificity has far-reaching consequences. In particular, the random filamentary structure of the current-carrying channels to a large extent renders meaningless the concept of bulk conductivity because the conductivities of filaments and of the rest polymer are significantly different, so that simple averaging may give an inadequate idea on the characteristics of the composite medium and lead to erroneous estimates. At the same time, in our opinion, of particular interest are the investigations of dependence of polymer film conductivity on film thickness at fixed other parameters of the problem, which can provide additional useful information about the possible physical mechanisms of the observed conductance of current- carrying channels.

Research in this direction were carried out by the authors in[8-11] for practically important case of films of plasticized PVC, which is currently one of the most widely used polymers. In particular, developing new methodological approach and using an efficient plasticizer, the so-called "modifier A" (see below), which allows one to obtain plasticized PVC with sufficiently high electrical conductivity, unachievable with conventional plasticizers, in[8-11] it was able to obtain the most characteristic effects for WBP and to investigate the "pure" bulk conductivity of polymer samples in flexible PVC films with thickness 20-400 microns.

In[8] low-voltage transitions in HCS (far from breakdown threshold ) and high-voltage transitions (near threshold) were considered separately. The latter are not specific only for polymers and, as it is known, are realized for any insulators. In an area of the field strength close to the breakdown (for thin polymer films it is units volt), for a variety of organic substances, including polymers, there are quite extensive studies of the switching between conductivity states. For large ballast resistances and low currents (of the order of several nanoamper) a "soft" breakdown is realized, which is reversible and does not lead to any visible damage of the sample, even when repeated many times switching. At low field strengths for PVC plasticates spontaneously switching processes to the HCS have been reported in[9] at voltages of hundreds of times below threshold. Such spontaneous transitions can be regarded as giant (three or more orders of magnitude) non-thermodynamic fluctuations which occur for thickness of polymer films from 20 microns. At the same samples stimulated transitions to HCS were obtained, which are realized with high probability by applied pulsed voltage. Another important feature of WBP - the transition to conducting state upon application of uniaxial pressure was demonstrated in[10]. It should be noted that for films thickness of an order of 20 μm the dependence of conduction upon applied uniaxial pressure has step-wise character, while for thicker films of the order 50 μm it has almost proportional dependence.

In this paper, in continuation of[8-11], we study the behavior of the electrical conductivity of plasticized PVC films depending on the concentration of plasticizer and the film thickness. Abrupt changes in electrical conductivity of PVC-films with a smooth change in the concentration of plasticizer was firstly detected, i.e., in accordance with the modern concepts of the plastification[12,13], as a result of a smooth increase in the number of kinetically mobile segments of macromolecules. For plasticizer concentrations corresponding to HCS the results of study of electrical conductivity show a simple exponential dependence on thickness, which in our opinion, enables to relate the mechanism of the observed phenomena with the rise of con- ductive nano-channels in polymer volume. The observed transition in HCS to a certain extant is analogous to the well-known transition of gas diffusion coefficient through polymer films. This effect is known to arise from nanoscopic fractal porosity of polimer materials, and high gas transmition value arises due to the channel formation from one side of film to another. Nearly the same physics may be responsible for electric conductivity switching in explanation of this phenomena developed in this paper, which is based on the hypothesis of charge transfer by nanoscale kinetic segments of polymer macromolecules.

2. Experimental

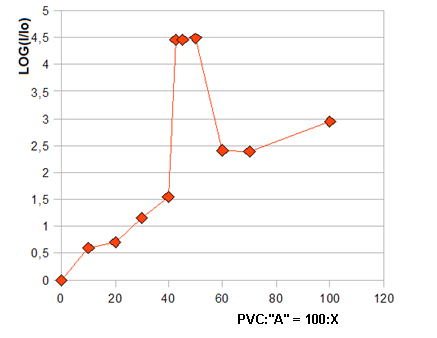
Measurements of conductance were made for a set of films with identical thickness 20 microns, but various mass ratio of PVC and plasticizer (mass fractions PVC: Modifier "A" == 100:0-100, respectively). The commercially available high-performance modifier "A" was used as plasticizer[14], which belongs to a class of esters of monocarboxylic acids and glycols and has a higher plasticizing ability than the more common PVC plasticizers such as DOP or DOA[12,13]. Using this plasticizer elastic, transparent, hydrophobic films were obtained with antistatic level of conductivity.

As starting PVC the suspended powder С70-59М was used, which has high porosity of granules (that in a case of sorption plasticization provides high ability to plasticizer absorption) and narrow molecular-mass distribution (the Fikentscher constant varies within 70-71). Both of these components were dissolved completely in tetrahydrofuran (THF), forming true homogeneous 4 % solution. Next, the sample films were obtained by pouring onto a glass substrate, followed by prolonged drying in an oven with a temperature of 50℃. Measurements of the current-voltage characteristic (CVC) were carried out in accordance with the recommendations of the GOST -Standard using the simplest scheme[8] and a standard circular cell. In this case the CVC were analyzed for samples with different mass fractions of plasticizer at voltages from zero to a maximum of 124 V. All conductivity measurements were carried out at a fixed pressure, the same for all samples with different mass fractions of the plasticizer (the details of measurements are described in[8-10]).

The most interesting of the obtained results is an unusual dependence of conductivity (current through the film) from the mass fraction of plasticizer. The experimental points show an anomalous zone in which there is a sharp transition to a state of high conductivity (Fig. 1), i.e. transition from the level of insulator to the semiconductor level. The resistance of the 20 μm film sample for weight part 42.5 - 50 Modifier "A" (per hundred parts of PVC) in the this state was only about R ~ 100 Ohms. If conventionally calculate the resistivity ρ (assuming that the conductivity depends linearly on the thickness), we find ρ ~ 10⁵ Ohm-cm, which corresponds to a semiconductor. Thus, we can say that the rise of plasticiser concentration stimulates the sharp transition to HCS, ie converts the classic insulator into semiconductor conduction area. Further, except for this relatively narrow zone of concentrations corresponding to low-resistance state, with an increase of the proportion of plasticizer there is a sharp return to its original state with a resistance corresponding units - tens GOhm (which, in particular, greatly exceeds the ballast 3.3 MOhm).

Figure 1. The dependence of current through the plasticized PVC film with thickness 20 microns at a voltage of 124 V. The abscissa - the mass fraction of the modifier "A", the ordinate axis - logarithm ratio of current to the average current fluctuations (with a standard external resistance[8])

Thus, in accordance with the results, on the dependance of the conductivity of the polymer film from the mass fraction of plasticizer one can select three zones: a zone of "depleted" mass fraction of plasticizer (0-42.5) - in the normal state conductivity is low (R ~ 10¹¹ -10 ⁹ Ohms) ; zone "resonant" mass fraction (42.5-50) - in the initial state the conductivity is high (~ 100 Ohms); and a zone with the "excess" plasticizer content (50 and above) - in the initial state conductance at the level of antistatic (R ~ 10⁶ -10¹⁰ Ohms).

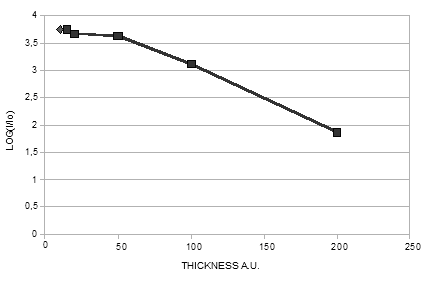Figure 2. Experimental dependence of the current from the sample thickness. The abscissa - thickness of the sample in arbitrary units close to microns, the ordinate axis - logarithm of current

Measurements of the conductivity (current through the film) for a set of films with different thickness from 20 to 200 μm, were made for the ratio of PVC: Modifier "A" = 100:45, which corresponded to areas of initially-high ("resonance") conductivity of the film. These measurements were performed for different voltages in the range from a few to 124V. The current in measuring circuit was proportional to the voltage, i.e. nonlinear effects were absent. Experiments with different samples were carried out at a fixed temperature and pressure. A typical dependence of current through the sample compound on the film thickness is shown in Fig.2 in logarithmic (on the ordinate axis) scale. From a Fig. 2 it is visible that the behavior of a current for sufficiently large L from L ~ 50 μm is well approximated by a simple exponential dependence.

3. Results and Discussions

The experimentally observed sharp increase in conductivity occurs when mixing of two insulators - PVC and plasticizer, which do not form chemical bonds with each other, so that the explanation of the conductivity jumps is logical to base on the attraction of physical mechanisms of both plasticization process and electrical conductivity of polymer plasticate. We show that qualitatively this explanation can be constructed on the basis of classical percolation theory, linking the emergence of jumps with the passage of "direct" and "reverse" percolation thresholds. This explanation is largely independent on the details of microscopic mechanisms, since it uses only an assumption that plasticizing of PVC originate two phases - effectively conducting phase and the phase of insulator, so that extreme cases of low plasticizer content (pure PVC) and large (pure plasticizer) correspond to an insulator.

In support of this assumption it is possible to make following observations. At the present time there are several far from definitive theories of plasticization[12,13]. Common to them is to explain the growth of the mobility of kinetic segments of macromolecules on the basis of different physical mechanisms, such as weakening of the hydrogen or van der Waals forces, the effects of lubrication or increase in free volume. On the other hand, it is known that during evaporation of solvent from the true homogeneous molecular solution of polymer, macromolecules begin to merge into nano-sized clusters with a fractal structure, and in this sense plastic compound is highly nonuniform at the nano-micro level[15]. In particular, the PVC forms closed clusters, and a plasticizer (not forming clusters) "wets" their surface and partially fills the free space between them, thus ensuring the flexibility of polymer matrix by increasing the mobility of nano-sized segments of macro-molecules.

According to a model of electrical conductivity of PVC developed by authors in[8-11], just the kinetic segments provide mobility of charge traps in the macromolecule, that are fixed in the absence of plasticizer. In turn, mobile traps provide local charge transfer within the boundaries of segment mobility. Thus, the described "plasticate" conductivity should occur primarily in the areas of maximum concentration of mobile segments, i.e. in the border areas between two insulators - clusters of PVC and plasticizer.

For low content of plasticizer the gradual increase of the last can be regarded as the introduction of conductive elements in isolator medium (PVC), i.e. we obtain a classical variant of the percolation[16] with an appropriate threshold for the formation of infinite conducting cluster and the abrupt, almost discontinuous increase in conductivity. On the contrary, for excess of plasticizer, adding a cluster of PVC surrounded by plasticizer is equivalent to adding conductive element in an insulator, which again allows us to interpret the concentration dependence of the conductivity (now PVC clusters in plasticizer) as a problem of percolation theory with the corresponding percolation threshold - a sharp increase in conductivity. If we consider a one-way process of increasing the mass fraction of plasticizer in PVC, we have two percolation thresholds: the first - for ordinary percolation theory - the "direct" - corresponding to an abrupt transition to higher conducting state, and second - a specific for the case of plasticate - "reverse" - corresponding to return of conduction to the insulator level. Thus, within the qualitative model one can predict the existence of the two jumps in conductivity, which is fully consistent with the experimental data.

In this model, in contrast to classical formulation of percolation theory problem, the effective content of conducting phase is not given directly, but depends on the contents of plasticizer, and vanishes at high and low concentrations of the latter. Determination of the explicit form of this dependance requires further specification of the model.

It should be noted that the involvement of percolation theory in a simple phenomenological form, namely, the Bruggeman effective medium approximation, for a model of spherical conductive inclusions gives for the percolation threshold the volume fraction of conducting phase 1 / 3, irrespective of the conductivity. This on a quantitative level agrees with the region of percolation transitions in Fig. 1, if we assume that the conducting phase is limited by the smallest of the two plasticate fractions. However, this quantitative agreement is rather accidental and should not be interpreted in favor of a model of isotropic - spherical conductive clusters, because a strong anisotropy of the geometry of micro-clusters in this case seems much more probable in view of the linear structure of PVC macromolecules.

Turning to the discussion of Fig. 2, note that a similar investigation in the case of submicron poly (diphenylenephthalide) films, made in[4], have demonstrated the dependence of the electrical conductivity of the film thickness L of the form L^-3, which served as an important argument in favor of a model of space-charge-limited injection currents. In earlier work[17] for films of Dacron exceeding a certain characteristic thickness at a pressure of several kilobars was found the exponential dependence of the resistance of the square of the thickness L², which is well described by proposed in[17] model pressure stimulated injection of carriers from metal into the conduction band.

In contrast to these results, in this paper according to Fig.2 for relatively thick films of plasticized PVC the simple exponential dependence of film resistance on L is most characteristic, which practically excludes the strong effect of space-charge-limited currents on film conductivity. This dependence can be explained within the framework of a rather general phenomenological model of independent conductive channels occurring in polymer volume. For an explanation of the received dependence of film conductivity from thickness it is possible after[18] to obtain such dependence basing solely on the hypothesis of existence in the volume of polymer random distribution of "conduction channels".

Denote by f (L) the number of conducting channels that pass through the entire thickness L of the film. It is natural to assume that these channels are independent and the exit sites of these channels on the surface are random. We partition mentally the considered film on two with thicknesses L₁ and L₂, L₁+ L₂ = L. Then the number of channels per unit area will be equal to, respectively, f (L₁) and f (L₂). But not on all channels the current can flow through both films, but only on those that pass through the entire thickness of the polymer.

In other words, the current can pass through only those channels that meet at the interface between the film thickness of L₁ and L₂. We will count the number of such channels. Let the total area of a considered site is equal S, and the area of a surface of one channel (cross section) σ. Then the number of channels in the first film is f (L₁) S, in the second f (L₂) S. Calculate the probability that any allocated channel from the top film will meet any channel from the bottom film. For this channel of the bottom film should get into the area around the chanal of the upper film, surface of this zone is 4σ. The average number of channels (or more precisely, the expected number of channels) on the bottom of the film area is equal to 4σ f (L₂) 4σ. The number of such sites is the number of channels of the upper film, ie, f (L₁) S. Thus, the number of channels that meet each other above and below f (L₁) S f (L₂) 4σ is equal to f (L) S. The result is a functional equation for f (L)

f(L₁+L₂)=4σ f(L₂ ) f(L₁)

This equation has the solution

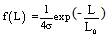Here the preexponential factor is determined from the functional equation uniquely, and L₀ - an arbitrary parameter with dimensions of length, having a sense of full length of the conducting channel along the normal to the film surface. Since the conductivity of the film is proportional to the function f (L), this expression describes the basic dependence of a current through a film from its thickness at constant pressure.

The considered estimate was obtained in very rough assumptions - for example, the channels may intersect almost the entire area, or can only touch each other, and these cases are considered equal. This will be reflected on the fact that the preexponential factor is not 4σ, but σ with some other factor. Here we have neglected also the boundary effects (i.e., the fact that near the real border of polymer channels can behave not like inside), so that channels may not be independent, that the different layers can not be independent, that channels can be of different sizes, etc. Another condition for the applicability of the model under consideration is a sufficient thickness of the film, which must be greater than the length of independent conduction channels. This condition excludes, in particular, consideration of thin films with the thickness of the order of the "elementary" channel, which plays the role of "microscopic length" in relation to the "macroscopic" length L₀.

The observed exponential dependence partly explains the common desire to work with thin films, as in thicker films due to the exponential dependence the current and its changing is extremely difficult to register. Another important consequence of these results is the previously experienced significant limitation of the concept of specific bulk conductivity (resistance) for the measurements of thin-film polymers, because the length (thickness) of the sample is included in the formula under the exponent.

5. Conclusions

In the given work the jumps in conductivity of plasticized PVC films with smooth increase of plasticizer concentration were first observed. The detection of an area with relatively high conductivity has allowed to carry out conductivity measurements in a wide range of thickness from 20 to 200 μm. The analysis of experimental results has found out unusual exponential dependence of conductivity on film thickness.

To explain the observed anomalies in electrical conductivity the phenomenological model was proposed, which associates the observed jumps with development in bulk polymer of nano-sized conductive channels, caused by increasing mobility of charge traps under the influence of plasticizer. This model allowed to explain the observed changes in conductivity as “direct" and "inverse" percolation transitions, and can be useful for description of physical properties of composite films including various plasticized polymers, which have in the dielectric volume independent channels of conductivity.

ACKNOWLEDGEMENTS

This work was supported by grant 07-02-00568-a of the Russian Foundation for Basic Research.