| [1] | Merrill, W., Schneider, N., 1966. Government firms in oligopoly industries. Quarterly Journal of Economics 80 (3), 400-412. |
| [2] | Ware, R., 1986. A model of public enterprise with entry. Canadian Journal of economics 19 (4), 642-655. |
| [3] | Sertel, M. R., 1988. Regulation by participation. Journal of Economics 48 (2), 111-134. |
| [4] | Cremer, H., Marchand, M., Thisse, J.-F., 1991. Mixed oligopoly with differentiated products. International Journal of Industrial Organization 9 (1), 43-53. |
| [5] | Delbono, F., Rossini, G., 1992. Competition policy vs horizontal merger with public, entrepreneurial, and labor-managed firms. Journal of Comparative Economics 16 (2), 226-240. |
| [6] | Delbono, F., Denicolò, V., 1993. Regulating innovative activity: the role of public firm. International Journal of Industrial Organization 11 (1), 35-48. |
| [7] | Nett, L., 1994. Why private firms are more innovative than public firms. European Journal of Political Economy 10 (4), 639-653. |
| [8] | Willner, J., 1994. Welfare maximization with endogenous average costs. International Journal of Industrial Organization 12 (3), 373-386. |
| [9] | Delbono, F., Scarpa, C., 1995. Upward-sloping reaction functions under quantity competition in mixed oligopolies. Bulletin of Economic Research 47 (4), 341-346. |
| [10] | Pal, D., 1998. Endogenous timing in a mixed oligopoly. Economics Letters 61 (2), 181-185. |
| [11] | Poyago-Theotoky, J., 1998. R&D competition in a mixed duopoly under uncertainty and easy imitation. Journal of Comparative Economics 26 (3), 415-428. |
| [12] | Fjell, K., Heywood, J. S., 2002. Public Stackelberg leadership in a mixed oligopoly with foreign Firms. Australian Economic Papers 41 (3), 267-281. |
| [13] | Bárcena-Ruiz, J. C., Garzón, M. B., 2003. Mixed duopoly. Merger and multiproduct firms. Journal of Economics 80 (1), 27-42. |
| [14] | Matsumura, T., 2003. Endogenous role in mixed markets: a two-production-period model. Southern Economic Journal 70 (2), 403-413. |
| [15] | Dadpay, A., Heywood, J. S., 2006. Mixed oligopoly in a single international market. Australian Economic Papers 45 (4), 269-280. |
| [16] | Ohnishi, K., 2010. Domestic and international mixed models with price competition. International Review of Economics 57 (1), 1-7. |
| [17] | Bös, D., 1986. Public Enterprise Economics. North-Holland, Amsterdam. |
| [18] | Bös, D., 2001. Privatization: A Theoretical Treatment. Clarendon Press, Oxford. |
| [19] | Vickers, J., Yarrow, G., 1988. Privatization: An Economic Analysis. MIT Press, Cambridge MA. |
| [20] | Cremer, H., Marchand, M., Thisse, J.-F., 1989. The public firm as an instrument for regulating an oligopolistic market. Oxford Economic Papers 41 (1), 283-301. |
| [21] | Nett, L., 1993. Mixed oligopoly with homogeneous goods. Annals of Public and Cooperative Economics 64 (3), 367-393. |
| [22] | Gronberg, T. J., Hwang, H., 1992. On the privatization of excludable public goods. Southern Economic Journal 58 (4), 904-921. |
| [23] | Fjell, K., Pal, D., 1996. A mixed oligopoly in the presence of foreign private firms. Canadian Journal of Economics 29 (3), 737-743. |
| [24] | George, K., La Manna, M., 1996. Mixed duopoly, inefficiency, and public ownership. Review of Industrial Organization 11 (6), 853-860. |
| [25] | White, M. D., 1996. Mixed oligopoly, privatization and subsidization. Economics Letters 53 (2), 189-195. |
| [26] | Poyago-Theotoky, J., 2001. Mixed oligopoly, subsidization and the order of firms’ moves: an irrelevance result. Economics Bulletin 12 (3), 1-5. |
| [27] | Myles, G., 2002. Mixed oligopoly, subsidization and the order of firms’ moves: an irrelevance result for the general case. Economics Bulletin 12 (1), 1-6. |
| [28] | Tomaru, Y., 2006. Mixed oligopoly, partial privatization and subsidization. Economics Bulletin 12 (5), 1-6. |
| [29] | Kato, K., Tomaru, Y., 2007. Mixed oligopoly, privatization, subsidization and the order of firms’ moves: several types of objectives. Economics Letters 96 (2), 287-292. |
| [30] | Anderson, S. P., de Palma, A., Thisse, J.-F., 1997. Privatization and efficiency in a differentiated industry. European Economic Review 41 (9), 1635-1654. |
| [31] | Matsumura, T., 1998. Partial privatization in mixed duopoly. Journal of Public Economics 70 (3), 473-483. |
| [32] | Mujumdar, S., Pal, D., 1998. Effects of indirect taxation in a mixed oligopoly. Economics Letters 58 (2), 199-204. |
| [33] | Pal, D., White, M. D., 1998. Mixed oligopoly, privatization, and strategic trade policy. Southern Economic Journal 65 (2), 264-281. |
| [34] | Sasaki, D., Wen, M., 2003. On optimal privatization. In: Baldassarri, M. and Lambertini, L. (Eds.), Antitrust, Regulation and Competition. Palgrave Macmillan, New York, pp. 193-216. |
| [35] | Bárcena-Ruiz, J. C., Garzón, M. B., 2005. Economic integration and privatisation under diseconomies of scale. European Journal of Political Economy 21 (1), 247-267. |
| [36] | Bosi, S., Girmens, G., Guillard, M., 2005, Optimal privatization design and financial markets. Journal of Public Economic Theory 7 (5), 799-826. |
| [37] | Chang, W. W., 2005. Optimal trade and privatization policies in an international duopoly with cost asymmetry. Journal of International Trade and Economic Development 14 (1), 19-42. |
| [38] | Chao, C. C., Yu, E. S. H., 2006. Partial privatization, foreign competition, and optimal tariff. Review of International Economics 14 (1), 87-92. |
| [39] | Han, L., Ogawa, H., 2008. Economic integration and strategic privatization in an international mixed oligopoly. FinanzArchiv 64 (3), 352-363. |
| [40] | Roy chowdhury, P., 2009. Mixed oligopoly with distortions: first best with budget-balance and the irrelevance principle. Economics Bulletin 29 (3), 1885-1900. |
| [41] | Wang, L. F. S., Wang, Y., Zhao, L., 2009. Privatization and efficiency gain in an international mixed oligopoly with asymmetric costs. Japanese Economic Review 60 (4), 539-559. |
| [42] | Bárcena-Ruiz, J. C., 2007. Endogenous timing in a mixed duopoly: price competition. Journal of Economics 91 (3), 263-272. |
| [43] | Barcena-Ruiz, J. C., Garzón, M. B., 2007. Capacity choice in a mixed duopoly under price competition. Economics Bulletin 12 (26), 1-7. |

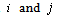 are used to refer to firms in an expression, they should be understood to refer to 0 and 1 with
are used to refer to firms in an expression, they should be understood to refer to 0 and 1 with 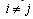 .There is no possibility of entry or exit. On the consumption side, there is a continuum of consumers of the same type whose utility function is linear. Following[42, 43], we assume that the representative consumer maximizes
.There is no possibility of entry or exit. On the consumption side, there is a continuum of consumers of the same type whose utility function is linear. Following[42, 43], we assume that the representative consumer maximizes 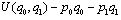 , where
, where 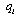 is the amount of good
is the amount of good 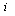 and
and 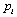 is its price. The function
is its price. The function 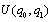 is quadratic, strictly concave and symmetric in
is quadratic, strictly concave and symmetric in 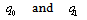 :
: 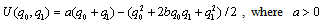 and
and 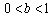 . The demand function is given by
. The demand function is given by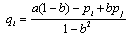
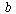 is a measure of the degree of substitutability among products. For the sake of simplicity, we assume
is a measure of the degree of substitutability among products. For the sake of simplicity, we assume 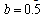 . Each firm’s profit is given by
. Each firm’s profit is given by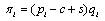
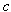 is the total cost for each unit of output and s s the subsidy for each unit of output. We assume
is the total cost for each unit of output and s s the subsidy for each unit of output. We assume 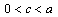 to assure that the production levels of firms are positive.Social welfare, defined as the sum of consumer surplus plus profits less the cost of subsidy, is given by
to assure that the production levels of firms are positive.Social welfare, defined as the sum of consumer surplus plus profits less the cost of subsidy, is given by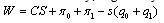
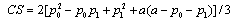 We consider four regimes: mixed and private duopoly, each with and without subsidies. In the regimes without subsidies, a simple Bertrand price-setting game is constructed and solved. In the regimes with subsidies, a two-stage game is constructed, wherein the government sets the subsidy in the first stage, and in the second stage each firm observes the subsidy and simultaneously chooses its price.
We consider four regimes: mixed and private duopoly, each with and without subsidies. In the regimes without subsidies, a simple Bertrand price-setting game is constructed and solved. In the regimes with subsidies, a two-stage game is constructed, wherein the government sets the subsidy in the first stage, and in the second stage each firm observes the subsidy and simultaneously chooses its price. to maximize social welfare (3), and in the private duopoly models (Subsections 3.3 and 3.4), it is privatized and therefore maximizes its own profit (2).
to maximize social welfare (3), and in the private duopoly models (Subsections 3.3 and 3.4), it is privatized and therefore maximizes its own profit (2). ), the Bertrand equilibrium values of prices, outputs, profits, consumer surplus and welfare are presented as follows:
), the Bertrand equilibrium values of prices, outputs, profits, consumer surplus and welfare are presented as follows: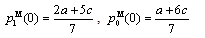
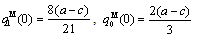
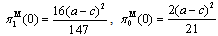
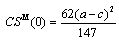
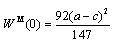
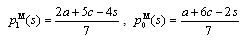
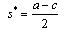
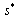 is strictly positive. Therefore, the government will always grant a positive subsidy.From (9) and (10), we derive the following subgame perfect Nash equilibrium outcomes:
is strictly positive. Therefore, the government will always grant a positive subsidy.From (9) and (10), we derive the following subgame perfect Nash equilibrium outcomes: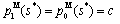
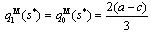
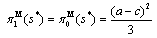
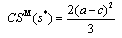
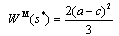
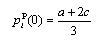
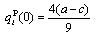
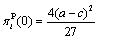
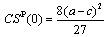
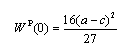
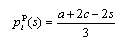
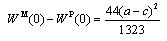
 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-Text HTML
Full-Text HTML