-
Paper Information
- Next Paper
- Paper Submission
-
Journal Information
- About This Journal
- Editorial Board
- Current Issue
- Archive
- Author Guidelines
- Contact Us
Journal of Logistics Management
2014; 3(1): 1-10
doi:10.5923/j.logistics.20140301.01
Evaluating Potential Freight Villages in Istanbul Using Multi Criteria Decision Making Techniques
Bahadır Fatih Yildirim, Emrah Önder
School of Business, Department of Quantitative Methods, Istanbul University, Istanbul, 34322, Turkey
Correspondence to: Emrah Önder, School of Business, Department of Quantitative Methods, Istanbul University, Istanbul, 34322, Turkey.
| Email: |  |
Copyright © 2012 Scientific & Academic Publishing. All Rights Reserved.
Evaluating freight villages and selecting one of them are complicated tasks due to the fact that various criteria or objectives must be considered in the decision making process. Also in many real world cases the criteria are not equally important for the logistic managers and government authorities. In this study, we proposed a freight village analysis model considering both Analytic Hierarchy Process (AHP) and PROMETHEE (preference ranking organization method for enrichment of evaluations) method. Subjective and objective opinions of logistic managers/experts turn into quantitative form with AHP. PROMETHEE technique is used for calculating the freight villages’ ratings. Apparently, freight village location selection is a multi-criteria problem that includes both quantitative and qualitative factors. It is necessary to make trade-off between these tangible and intangible factors while considering a suitable location. Accessibility, transport infrastructure, the value of freight villages (maritime connections, rail connections, road connections, and airport connections), distance from city center and total surface area are some of the key success factors of freight villages. The aim of this paper is to determine the appropriate freight village candidate providing the most satisfaction for the criteria identified in the supply chain management.
Keywords: Freight Villages, Logistic Management, Analytic Hierarchy Process, PROMETHEE, Multi Criteria Decision Making
Cite this paper: Bahadır Fatih Yildirim, Emrah Önder, Evaluating Potential Freight Villages in Istanbul Using Multi Criteria Decision Making Techniques, Journal of Logistics Management, Vol. 3 No. 1, 2014, pp. 1-10. doi: 10.5923/j.logistics.20140301.01.
Article Outline
1. Introduction
- Globalization and today’s competitive environment forces companies to reduce costs. The basic condition for increasing the competition and continuity in domestic and global markets is to control costs. Locations depots have a great effect on operating cost and price. The evaluation of a logistic village location among alternative locations is a multi-criteria decision-making problem including both quantitative and qualitative criteria. All the factors should be taken into consideration because of the fact that the decisions for location selection compel a government to work under same conditions for time. If official decision makers and authorities select the wrong logistic village location, it may not have adequate access to firms, workers, vehicles, agents, and so on. The general process for making location decisions usually is composed of the following steps[1]:1. Decide on the criteria that will be used to evaluate location alternatives.2. Determine the criteria that are important.3. Develop suitable location alternatives.4. Evaluate the alternatives and make a decision.The aim of this paper is to identify the appropriate location providing profitability and productivity for the logistic sector. In this paper, distance and proximity data calculated via googlemaps[2]. “Opportunities for possible site expansion” and “Cost of land” data was taken from http://www.igd.com.tr/ and “ekonomi.haber7.com”[3],[4]. All data is used to illustrate the logistic village evaluation procedure. We proposed a logistic village evaluation analysis using AHP and PROMETHEE methodologies. Subjective and objective opinions of experts turn into quantitative form with Analytic Hierarchy Process. AHP is applied to determine the relative weights of the evaluation criteria. In this study, Bamyaci’s weights of criteria were utilized[5]. PROMETHEE technique is used for calculating the locations’ ratings.This paper is arranged into five sections. The second section provides an overview of existing methods and studies. The third section shows the structure of the problem in Turkey. The next section describes the proposed approach and gives information about AHP and PRMOMETHEE methodologies. In section five, an empirical study is illustrated in İstanbul candidate logistic villages. Results of the study are presented in section six. Finally, concluding remarks and discussions follow.
2. Literature Review
- Several approaches have been proposed in the literature for solving the logistic/distribution center problems. Some of these methods and applications are mentioned below.Janic and Reggiani illustrates the application of three Multiple-Criteria Decision-Making (MCDM) methods (Simple Additive Weighting, Technique for Order Preference by Similarity to the Ideal Solution and Analytic Hierarchy Process) to the problem of the selection of a new hub airport for a hypothetical European Union (EU) airline[6]. Jaržemskis’s research focuses on logistics center concept and benefits for users. In this paper author presents intermodal benefit, forwarders impact, IT solutions, new transport flows due to synergy, better supply chain management, additional services, cost sharing, economies of scale, quality of the services, know-how, joint marketing impact, and benefit for growth of third-party logistics services[7].In the paper of Ballis and Mavrotas three alternative designs of the freight village layout are compared using the PROMETHEE method. The multicriteria framework consists of selecting the most meaningful criteria of evaluation and the required decision parameters. Results of their analysis reveal the preference order of the alternative designs[8].Lindholm and Behrends contribute to lay the groundwork for designing strategies to overcome the challenges involved in sustainable urban freight transport. Potentials and shortcomings in urban freight transport planning are presented and the results show that freight transport is increasingly important for regional competitiveness while freight traffic is a growing threat for urban sustainability[9].Cerreno et al.[10] emphasizes in determining the feasibility of Freight Villages for the NYMTC region. They investigated the NYMTC’s three goals (congestion mitigation, rational and efficient land use, and economic development) regarding location selection of Freight Villages[10]. Yanga et al.[11] investigates distribution centers location problem under fuzzy environment via chance-constrained programming model. They integrate tabu search algorithm, genetic algorithm and fuzzy simulation algorithm to seek the approximate best solution of the model[11]. Awasthi, Chauhan and Goyal[12] present a multi-criteria decision making approach for location planning for urban distribution centers under uncertainty. Their model starts with identification of potential locations, selection of evaluation criteria, than use of fuzzy theory to quantify criteria values under uncertainty and application of fuzzy TOPSIS to evaluate and select the best location for implementing an urban distribution center[12]. Li, Liu and Chen[13] present a comprehensive methodology for the selection of logistic center location. Their proposed methodology consists of two parts: Axiomatic Fuzzy Set clustering method for effectively evaluate logistics center location, and TOPSIS method for selection. Their case includes fifteen regional logistics center cities and thirteen criteria[13].Taniguchi et al.[14] describe a mathematical model developed for determining the optimal size and location of public logistics terminals using queuing theory and nonlinear programming techniques for finding the best solution. They applied their model to an actual road network in the Kyoto-Osaka area in Japan[14].Sirikijpanichkul and Ferreira[15] proposed a model to solve the conflicts in intermodal freight hub location decisions based upon the multi-objective evaluation techniques with other supporting established modules including land use allocation and transport network models; financial viability; hub user cost; and environmental and traffic impact modules[15].
3. Structure of the Freight Village Location Selection Problem
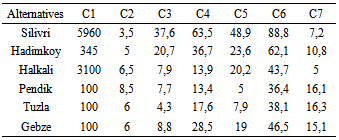
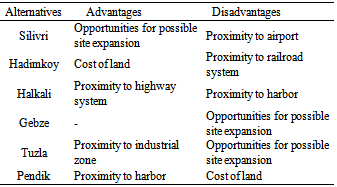
- Target of the government and logistic sector with the new investments, is find the optimum locations of the logistic villages. Capacity of current distribution centers cannot meet the customers/firms’ demand, for this reason all logistic sector actors’ management are planning building a new logistic villages in order to meet growing demand. The experts determined six freight village location alternatives for the new distribution centers including Silivri, Hadimkoy, Halkali, Pendik, Gebze and Tuzla. Criteria taken in to account for freight village selection are as follows:1. Opportunities for possible site expansion2. Cost of land3. Proximity to industrial zone4. Proximity to airport5. Proximity to harbor6. Proximity to railroad system7. Proximity to highway system
4. Proposed Methodology
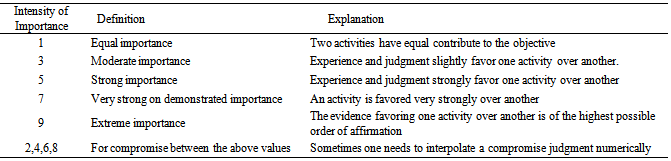
- AHP is an effective decision making method especially when subjectivity exists and it is very suitable to solve problems where the decision criteria can be organized in a hierarchical way into sub-criteria. The findings of previous studies about factors influencing experts’ choice of location of logistic villages were first identified by literature review. Experts expressed or defined a ranking for the attributes in terms of importance/weights. Each experts is asked to fill ‘‘checked mark’’ in the 9-point scale evaluation table. The AHP allows group decision making. AHP based weights were taken from Bamyaci’s research[5]. The questionnaires are answered by 42 experts (11 academicians, 13 public official logistic experts, 7 experts in customer firms, 11 experts of logistic firms). Experts are asked to compare the criteria at a given level on a pair-wise basis to identify their relative precedence.
4.1. Using AHP to Analyze Priorities
|
|
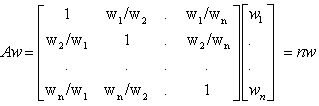 | (1) |
 | (2) |
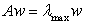 | (3) |
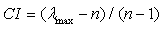 | (4) |
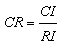 | (5) |
4.2. Using Preference Ranking Organization Method for Enrichment Evaluations (PROMETHEE) to Rank the Alternatives
- Preference Ranking Organization Method for Enrichment of Evaluations (PROMETHEE) method is developed by Brans (1982)[23] and further extended by Brans and Vincke (1985)[24]. It was partly designed as a reaction to the complete aggregation American Multi Attribute Utility Theory (MAUT) methods[25].PROMETHEE family of outranking methods are intended to provide a complete ranking of a finite set of feasible alternatives from the best to the worst. The methods of PROMETHEE have successfully been applied in many fields and used in decision-making problems.Behzadian et al. (2010)[26] have presented a comprehensive literature review in the current research on PROMETHEE methodologies and applications. They classified the PROMETHEE applications into Environment Management, Hydrology and Water Management, Business and Financial Management, Chemistry, Logistics and Transportation, Manufacturing and Assembly, Energy Management, Social, and Other Topics[27]. Three main PROMETHEE tools can be used to analyse the evaluation problem[28]:1. PROMETHEE I for partial ranking2. PROMETHEE II for complete ranking and 3. the GAIA plane for graphical representationPROMETHEE requires two additional types of information, namely[29]:● Information on the relative importance (i.e. the weights) of the criteria considered.● Information on the decision-maker’s preference function, which decision maker uses when comparing the contribution of the alternatives in terms of each separate criterion.There are six basic preference functions suggested by Brans, Vincke, and Mareschal (1986)[30] and shown on Figure 1. Six different preference function cover almost all the possible criteria[31]1. Usual criterion, 2. U-shape criterion, 3. V-shape criterion, 4. level criterion, 5. V-shape criterion and6. Gaussian criterion.
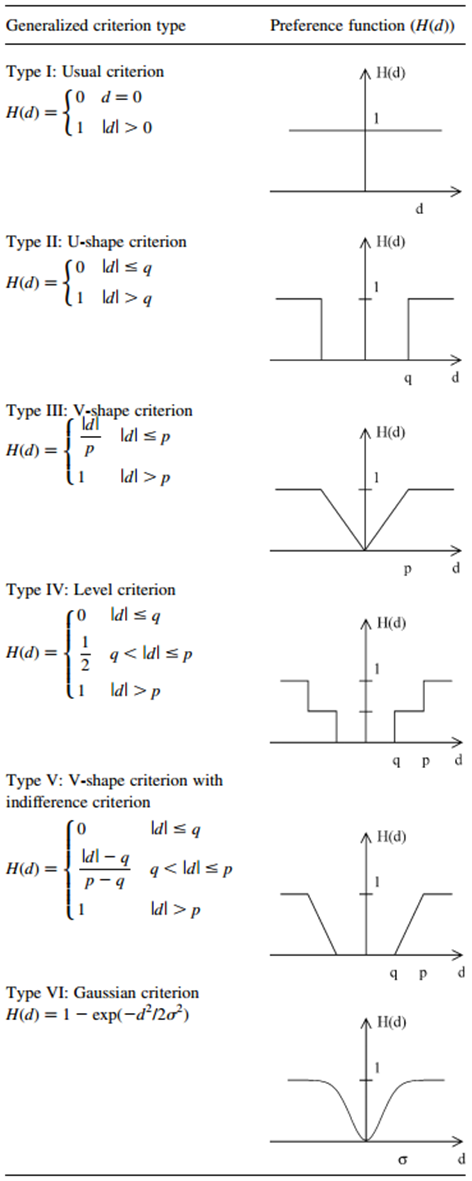 | Figure 1. PROMETHEE General Preference Functions[32] |
 | Figure 2. Stepwise procedure for PROMETHEE II[26] |
4.3. Combining AHP and VIKOR to Determine the Rank of Alternatives
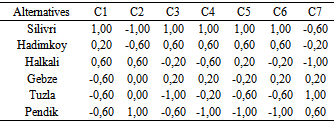
- In analyzing the data, Analytical Hierarchy Process (AHP) and PROMETHEE methodologies are used for the outranking of logistic village destination alternatives. Figure 3 shows the steps of the proposed method.
 | Figure 3. Steps of proposed method |
4.4. Solving Case Problem
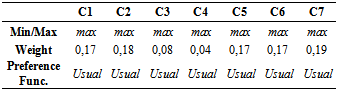
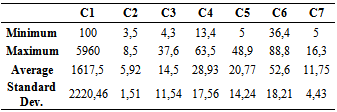
- To apply proposed method a real world logistic village location evaluation problem was solved. In this logistic village location evaluation problem there are 7 criteria and 6 candidate location including Silivri, Hadimkoy, Halkali, Pendik, Gebze and Tuzla. The hierarchical structure to select the best logistic village location is shown in Figure 4. In order to identify weights of the criteria previous academic research done by Bamyacı (2008) was used.Criteria to be considered in the evaluation of logistic village location are determined by literature review. It was very hard to evaluate some of qualitative criteria. Therefore in this research just quantitative criteria were investigated.7 important criteria to be used for logistic village location evaluation are established. These 7 criteria are as follows: “Opportunities for possible site expansion” (C1), “Cost of land” (C2), “Proximity to industrial zone” (C3), “Proximity to airport” (C4), “Proximity to harbor” (C5), “Proximity to railroad system” (C6) and “Proximity to highway system” (C7).As a result, only these 7 criteria were used in evaluation and decision hierarchy is established accordingly. Decision hierarchy structured with the determined alternative logistic village locations and criteria is provided in Figure 4. There are three levels in the decision hierarchy structured for logistic village location evaluation problem. The overall goal of the decision process is ‘‘ranking logistic village destination alternatives in Istanbul” in the first level of the hierarchy. The criteria are on the second level and alternative locations are on the third level of the hierarchy.After forming the decision hierarchy for the problem, the weights of the criteria to be used in evaluation process are calculated by using AHP method. In this phase, the experts in the expert team are given the task of forming individual pairwise comparison matrix by using the Saaty’s 1-9 scale.Geometric means of experts’ choice values are calculated to form the pairwise comparison matrix on which there is an agreement (Table 3). The results obtained from the calculations based on the pairwise comparison matrix provided, are presented in Table 3. The “C7: Proximity to highway system” (0.190) and “C2: Cost of land (0.180) are determined as the two most important criteria in the logistic village location selection process by using AHP. Consistency ratios of the experts’ pairwise comparison matrixes are all less than 0.1. So the weights are shown to be consistent and they are used in the selection process. The most important criterion is “C7: Proximity to highway system” (0.190) and the least important criterion is “C4: Proximity to airport” (0.040).
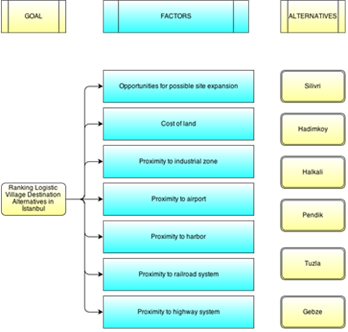 | Figure 4. Hierarchical Structure for Logistic Village Evaluation |
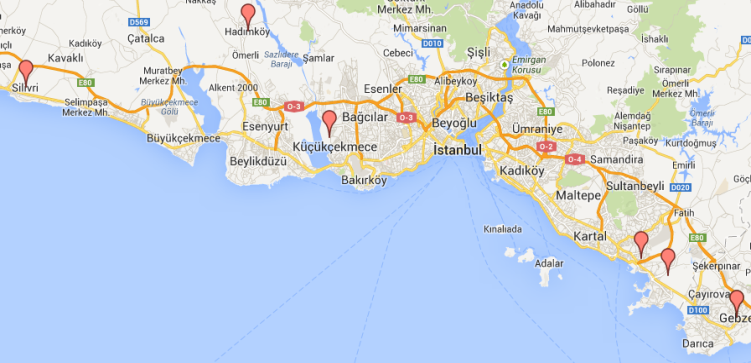 | Figure 5. Location alternatives of the problem |
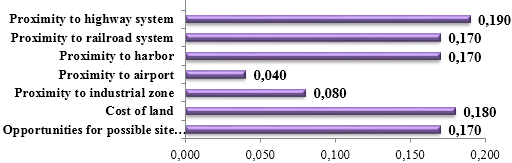 | Figure 6. Overall resulting weights of criteria obtained with AHP |
|
|
|
|
|
|
|
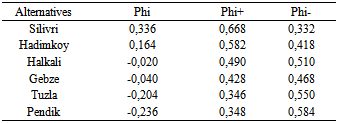
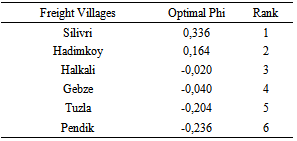
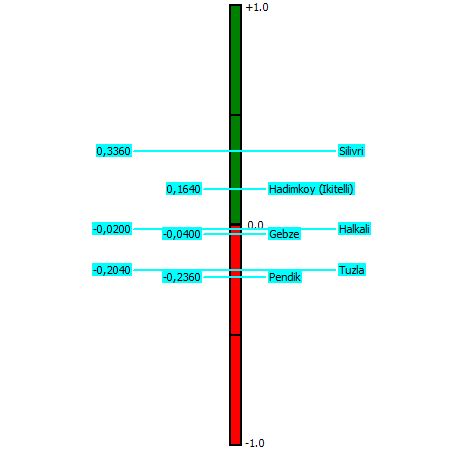 | Figure 7. Optimal Phi values obtained with PROMETHEE |
|
5. Conclusions and Suggestions
- Logistic village location decisions are very important part in any countries’ overall strategic plan. This paper presents a multi-criteria decision model for evaluating alternatives of logistic village destinations. For this purpose, a two-step methodology is introduced, in which the AHP determines importance level of criteria via expertise of decision making team members. Then, PROMETHEE method applies AHP’ weights as input weights. Finally, logistic village location problem was solved by using proposed method to show applicability and performance of the proposed methodology. Proposed model results show that Silivri is the best alternative with 0,336 Phi value. Depends on the analysis the least suitable logistic village is Pendik. By the compromise ranking method, the compromise solution is determined which would be most acceptable to the decision makers because it provides a maximum ‘‘group utility’’ for the ‘‘majority’’, and a minimum of individual regret for the ‘‘opponents’’. In next studies analytic network process (ANP) may be used to structure network and identify dependence among criteria. Extensions of the other MCDM techniques can be applied for decision making under fuzzy environment. The proposed methodology can also be applied to any other selection problem involving multiple and conflicting criteria. Selection of the logistic village location can also be done using other MCDM techniques for comparing the results.
 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML