Oluseun Oyeleke Wikiman1, Olabode Idowu-Bismark2, Sadiq Thomas1, Idris Muhammad3, Femi Ilesanmi2
1Dept of Computer Engineering, Nile University, FCT, Abuja, Nigeria
2Electrical & Information Engineering Dept, Covenant University, Ota, Ogun State, Nigeria
3Electrical Department, Nuhu Bamalli Polytechnic, Zaria, Nigeria
Correspondence to: Oluseun Oyeleke Wikiman, Dept of Computer Engineering, Nile University, FCT, Abuja, Nigeria.
| Email: |  |
Copyright © 2019 The Author(s). Published by Scientific & Academic Publishing.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/

Abstract
Massive MIMO is the massive use of antennas to increase spectral and energy efficiency and meet the fifth generation (5G) wireless mobile networks requirements. Massive MIMO capability to deliver data to multiple users and multiple mobile stations simultaneously while ensuring fast data rates and reliable performance makes it the most promising technology to address the requirements of the forthcoming 5G era. It is very important to carry out many analysis using a hybrid of realistic wireless propagation models so that performance analysis of large scale antenna wireless system can be obtained using these models. The performance of massive MIMO with Rician fading channels is much less analyzed unlike the Rayleigh fading and hence this paper seeks to further study massive MIMO Rician channel behavior. The main contribution of this paper is to investigate the performance of massive MIMO systems in a Rician channel using zero forcing precoder to enhance spectral efficiency and channel capacity. We show that massive MIMO can deliver high throguhput in a Rician channel as demostrated by the results of our simulation. Highest value of spectra efficiency from our simulation is gotten from k factor 2 which was measured from indoor hotspot by the WINNER II measurement campaign method. Theoretical values of k were also simulated to show that when line of sight (LOS) and non line of sight (NLOS) are equal, bit rate increases and also confirms that in a rich scattering enviroment diversity transmission actually thrives.
Keywords:
Massive MIMO, Rician Fading Channels, Zero Forcing, Rician K-Factor
Cite this paper: Oluseun Oyeleke Wikiman, Olabode Idowu-Bismark, Sadiq Thomas, Idris Muhammad, Femi Ilesanmi, Performance of Massive MIMO in a Rician Fading Channel Using a ZF Precoder, Journal of Wireless Networking and Communications, Vol. 9 No. 1, 2019, pp. 1-7. doi: 10.5923/j.jwnc.20190901.01.
1. Introduction
Massive multiple-input multiple-output (MIMO) systems equipped with large number of antennas at the base station (BS) have been proposed recently to handle the challenges of enormous data rates essential by the recent applications which are bandwidth-hungry [1]. Low transmit power, high spectral efficiency and simplified transmitter/receiver processing using algorithms such as match filter (MF), zero forcing (ZF) or minimum mean square error (MMSE) are gains offered by the large number of antennas at the BS in the massive MIMO system [2] [3]. Precisely, more than tenfold improvement in throughput can be obtained by the massive MIMO in comparison to long term evolution (LTE) network. Efficient Spatial domain exploitation was borne out of the increment in demand for high data rates with limitations of available bandwidth [4]. Antennas at access points are used to spatially discriminate the intended signals from channel impairments like noise and interferences. Throughput either on reception or transmission can be improved through the use of spatial diversity, in addition to letting spectral reuse on a higher degree and hence thereby increasing the system capacity [5] [6]. Massive MIMO systems utilizes base station (BS) antenna arrays, with hundreds of antenna elements, concurrently serving many tens of active terminals (users) using the same frequency and time resources. Massive MIMO has the potential to increase the capacity 10 times or even more and simultaneously increase the efficiency of energy radiated [7]. In a flat fading channel, multipath propagation produces constructive and destructive interference effect [8] and this is usually modeled using a Rayleigh distribution especially if there are no line of sight component. This of course is not accurate in practice as multipath propagation even in rich scattering has both independent identically distributed (i.i.d) scatters and also line of sight components [8]. In these scenarios the receiver receives signals which are scattered and reflected waves with varying random phases, path length and hence the received power is also a statistical variable. Once dealing with a LOS path, the strength of the LOS signal component is determined by the Rician factor [9]. Generally, theoretical research of Massive MIMO presumes i.i.d statistical scatters which are Gaussian complex variables and Rayleigh fading. As these is assumed, it can be difficult to justify [11]. In some situations. The achievable spectral efficiency (SE) of Massive MIMO systems with imperfect channel state information (CSI) have been thoroughly characterized and enhanced for fading channels modeled by either spatially uncorrelated [10] or spatially correlated Rayleigh fading [11]. However, in practical scenario, channels can be a combination of deterministic LOS path combined with small-scale fading as a result of multipath propagation, which can be modeled by the Rician fading model which is a frequency utilized alternative model for wireless channel where there are large line of sight components with large independent paths.Many authors has worked on different aspect of fading channels including [8] who developed algorithms for the Rayleigh and Rician fading channels which was used for the computation of received signal envelope outage probability. Results observed from the comparison table, demonstrates that the outage probability in the Rician fading channel is lesser than that of the Rayleigh fading channel and that the outage probability rises proportionally to the Doppler shift or mobile velocity. In the work of [12] the capacity performance of an antenna selection scheme employed in a massive MISO system was investigated using a Rayleigh fading channel for its analysis. [13] studied the merit of massive MIMO systems, they investigate the channel models of massive MIMO with different antenna array configurations under a Rayleigh fading channel, which can be used for both theoretical analysis and practical evaluation. Other authors include [14] who researched cooperative small cell network, and studied the fluctuations of the mutual information transmitted through a Rician fading channel under the form of a central limit theorem, and also providing for the asymptotic variance a clear expression, while [15] studied the asymptotic analysis of multi-cell Massive MIMO through Rician Channels. Numerical results from their study demonstrate the accuracy of these approximations. If employed in practical communication networks, such mathematical deductions can guide to vital insights into the behavior of the system especially with respect to the Rician factors which components are deterministic. The main contribution of this paper is to investigate the performance of massive MIMO system in a Rician channel using ZF precoder to enhance the spectral efficiency. The remaining part of this paper is outlined as follows. Section 2 discuss the Rician fading channels. Section 3 treat the methodology of our work while we presented the result of our simulations in section 4. The result analysis were presented in section 5 and we concluded in section 6.
2. Rician Fading Channels
The Rician fading propagation channel can be utilized to model wireless propagation when receiver can receive transmitted signal via a dominant line i.e. signals travelling in a direct path. As also expected in many occasion as well, direct signals travel with other multipath components. See figure 1. 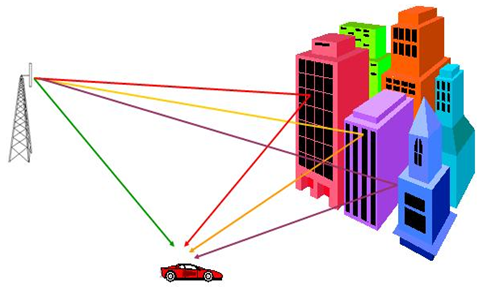 | Figure 1. Propagation with Rician Channel |
The impact of signal fading is observed as signal diffusion and scattering which results in receiver receiving multiple signals that has travelled though LOS and NLOS paths. Signals that travel as LOS are modeled as Rician fading channel. Rician K-factor parameter is used to describe the statistical model of a Rician distribution and it is the ratio between the LOS and NLOS power signals from the massive MIMO antennas and hence the K –factors divide the signal gain into scattered and direct components [16]. Rician K-factor does not exhibit substantial frequency dependence, hence their parameters show only dependence on environment of propagation (winner II report). The dominant LOS component in a Rician fading channel can be modeled by combining two Gaussian random variables i.e. one with zero mean and another with non-zero mean [17]. If we consider two Gaussian random variables a~N(mI, σ2) and b~N(mQ, σ2). Where µ1 and µ2 represents the means of the distributions and σ2 represents variance of the distribution. The probability density function or the magnitude of the received complex envelop at time t has a Rician distribution as shown in equation 1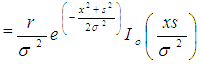 | (1) |
Where I0 is the modified Bessel function of the first kind with order zero and x as given in equation 2 | (2) |
is the non-centrality parameter. If s->0 that implies k-> 0 the Rice model process becomes a Rayleigh process of which the amplitudes of the received signal are being presented by a Rayleigh distribution. Assuming squares of k independent normal random variables with non-zero mean (mean µ=0, σ=1) are summed, it produces a non-central Chi-squared distribution. Non-centrality parameter is defined as the summation of means of each independent underlying Normal random variable (see figure 2).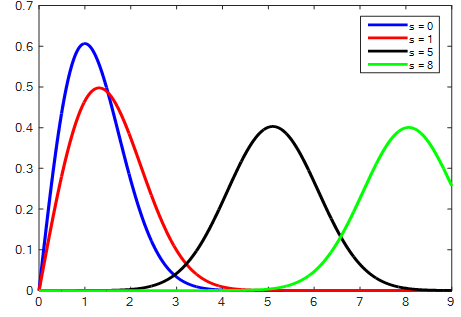 | Figure 2. Gaussian distribution with different non centrality parameter |
2.1. Non-Centrality Criteria
A basic Rician model makes the presumption that the mean mI and mQ representing the inphase and quadrature components of the received signal are invariable with time i.e. mI(t)=m and mQ(t)=m and the in-phase and quadrature component do not change with time as well. The means of the in-phase 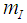 and mean of quadrature
and mean of quadrature 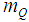 are given by
are given by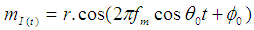 | (3) |
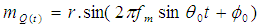 | (4) |
Where fm cosθ0 and Φ0 are the Doppler shift and random phase off set of the signal with the LOS component. The Rician K-factor is one of the major features of a wireless channel, and is defined as the ratio of the signal power of the line-of-sight (LOS) component to the signal power in the NLOS component and given by equation 5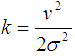 | (5) |
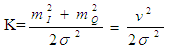 | (6) |
A Rician statistical channel can be mathematically described using the Ω and K parameter where 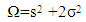 | (7) |
Is the total power from LOS and NLOS and K is the ratio of PLOS and PNLOS as in equation 8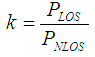 | (8) |
and it’s given in decibels the Rice factor, K, is defined as the ratio of the specular power 𝑠 2 to scattered power 2𝜎2 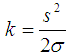 | (9) |
When k = 0 the channel is transformed into a Rayleigh fading, and when k = ∞ there is no fading in the channel. The envelope distribution can be rewritten in terms of the Rice factor and the average envelope power 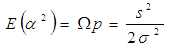 | (10) |
Where 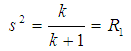 | (11) |
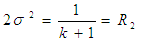 | (12) |
Therefore a basic Rician fading model can be described and simulated by setting variables R1 and R2 as seen in equation 13 and 14.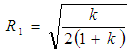 | (13) |
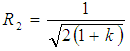 | (14) |
Therefore the theoretical PDF of the signal at the receiver channel can hence be rewritten as shown in equation 15.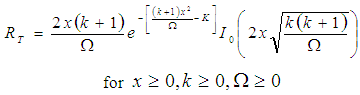 | (15) |
where I0 is the modified Bessel function of the first kind with order zero.
2.2. Zero Forcing Beamforming Algorithms
Interference is a possible challenge to be dealt with in Massive MIMO antenna systems. Zero-forcing is a signal processing technique that seeks to eliminate interference. This method allows the channel vectors which are not selected for transmission to be suppressed and hence ZF imposes stringent orthogonalization of all other user channel vectors [18]. Hence, ZFBF receives signals from the intended users and simultaneously nulls out interference from interfering users. This is why it is also referred to as interference nulling. ZFBF’s aim is to cancel all interferences between users [19]. The channel vector of the intended user is projected onto the orthogonal complement of the subspace (see figure 3) which is made up of rows. Interference need only to be canceled for active users. 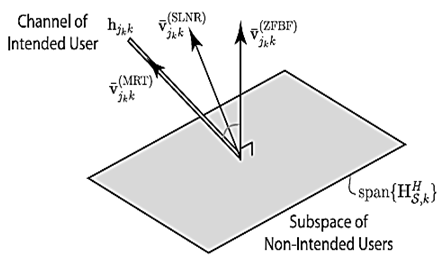 | Figure 3. Illustration of ZFBF channel vector projection |
The Maximum Ratio Transmitter (MRT) follows the channel of the active users and we can see that the ZFBF is orthogonal to the channel of the other active but non-intended users. The Maximum Signal-to-Leakage plus-Noise Ratio (SLNR-MAX) is a beamforming algorithm that maximizes the signal to leakage plus noise ratio and balances in-between the MRT and ZFBF.ZFBF can be defined using equation 16. 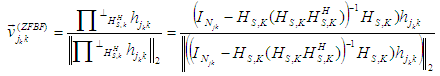 | (16) |
For all interference to be eliminated, the BF directions 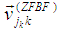 are generated by the projections of the channel vector
are generated by the projections of the channel vector 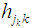 of the intended user on the orthogonal component of the space traversed by rows of channels of the intended users
of the intended user on the orthogonal component of the space traversed by rows of channels of the intended users 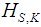 . (
. (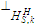 is the projection matrix unto the orthogonal complement of the column space) Since interference need to be cancelled for only active users, this is necessary for a scheduling set S.
is the projection matrix unto the orthogonal complement of the column space) Since interference need to be cancelled for only active users, this is necessary for a scheduling set S. 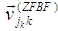 ,
,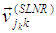 and
and 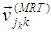 are the ZFBF, SLNR and MRT BF respectively [20].
are the ZFBF, SLNR and MRT BF respectively [20].
3. Methodology
The simulation will utilize codes used by [20] where the authors used a rayleigh fading channel, but this paper modified the codes to generate rician fading channel. The precoder used is the ZF precoder. Practical K factor values recorded from measurements conducted by the WINNER II model team will be used and simulated using MATLAB 2015a.Table 1. Simulation parameters
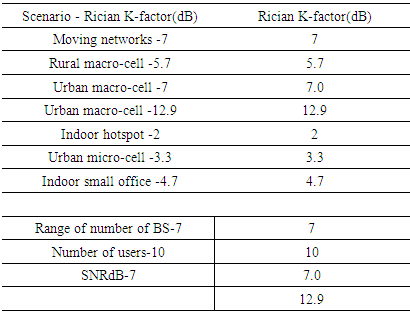 |
| |
|
4. Results
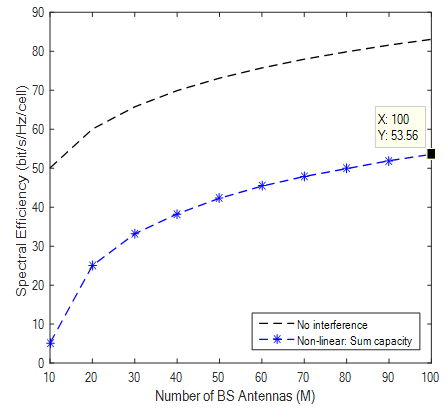 | Figure 4. SE with Rician Factor of 7 |
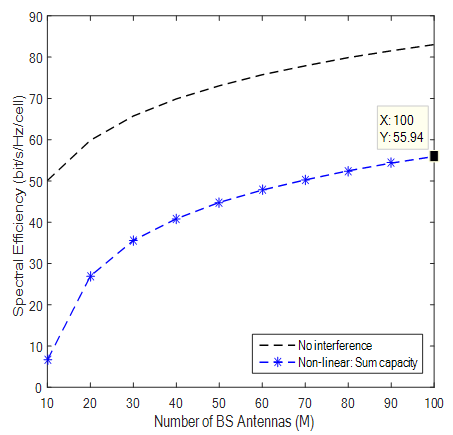 | Figure 5. SE with Rician Factor of 5.7 |
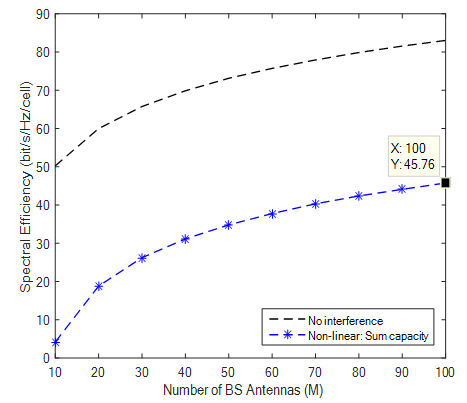 | Figure 6. SE with Rician Factor of 12.9 |
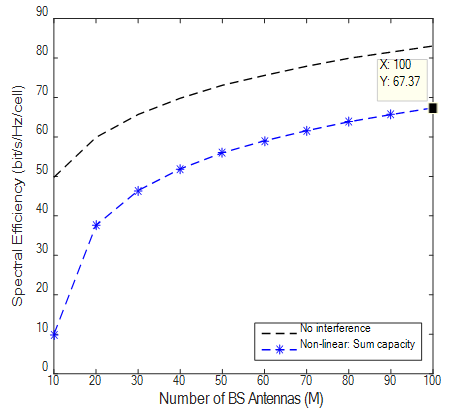 | Figure 7. SE with Rician Factor of 2 |
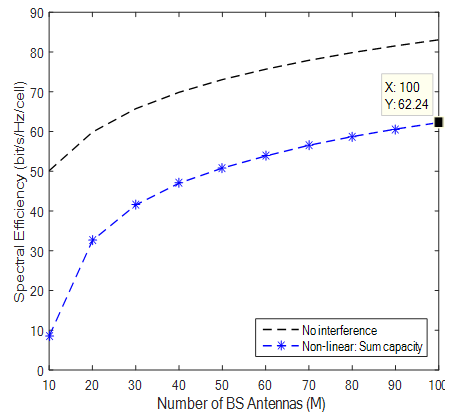 | Figure 8. SE with Rician Factor of 3.3 |
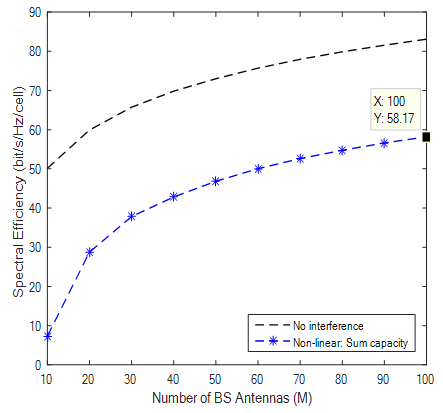 | Figure 9. SE with Rician Factor of 4.7 |
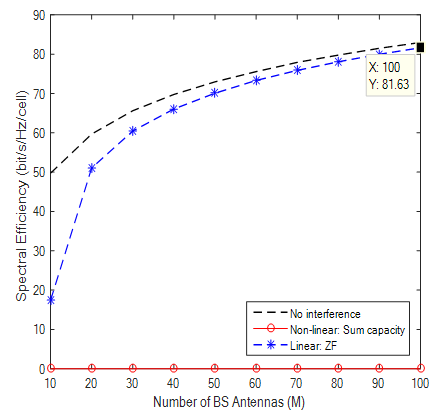 | Figure 10. Rayleigh fading |
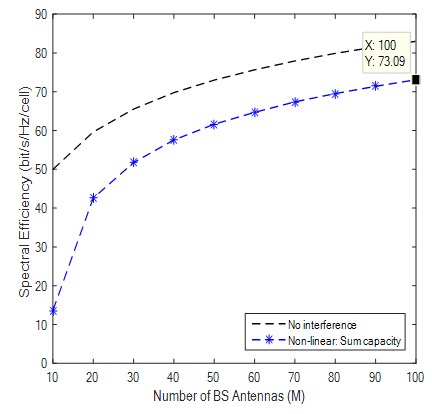 | Figure 11. SE with Rician Factor of 1 |
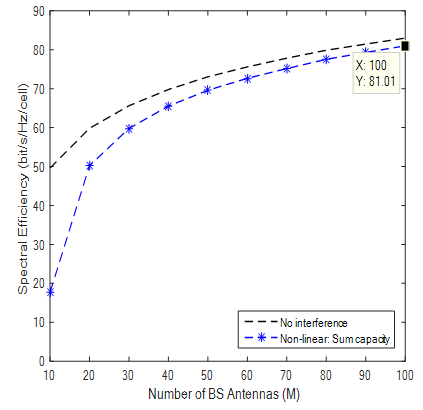 | Figure 12. SE with Rician Factor of 0.1 |
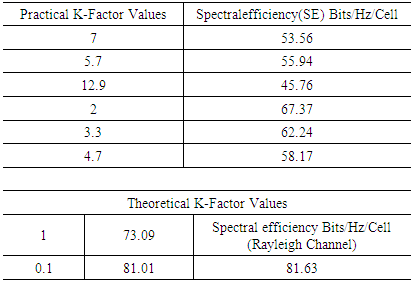
Table 2. Results of k-Factor and SE
 |
| |
|
5. Result Analysis
Results from simulations show different bit-rate for practical k-factor values. With K factor value of 7 the SE (bits/hz/cell) recorded was 53.59 and K value of 5.7 produces a SE of 55.94 and at K-Factor 3.3 and 4.7 SE was 62.24 and 58.17 respectively. It is observed that higher K Values like 12 produced lower SE compared to previous ones and results obviously demonstrated that the lower the K Value the higher the achievable rates recorded. Highest value of SE was shown when K factor is 2 which was measured from indoor hotspot by the WINNER II measurement campaign. Theoretical values of K were also simulated to show that when LOS and NLOS are equal bit rate increases and also confirms that in a rich scattering enviroment diversity transmission ACTUALLY THRIVES by taking advantage of multipath to deliver high throughput. Results also confirms that when K →∞ a Rician channel behaves like a Rayleigh channel. It should be noted that the highest SE of 67.37 with Rician K-factor of 2 comes from indoor hotspot environment which are wide with low mobility (0 -5 Km/h). Such environments like train stations, sport stadium, conference halls and airports are with high data traffic density and are characterized by large open spaces with significant BS/UE and UE/UE distances. These indoor environments could have space dimensions of not less than 20m by 20m but up to 100m by 100m with height in the region of 20m. Such environments though indoor, are expected to have both LOS and NLOS propagation conditions with high spectral efficiency and high throughput.
6. Conclusions
The aim of this paper is to study MASSIVE MIMO in Rician fading channel and justify the expectations of massive MIMO in being able to thrive in various fading channel taking advantage of spatial diversity to improve spectral efficiency. Result from extensive simulations shows that despite varying numbers of k-factors, high SE was still achieved. The results of the simulation shown in Fig 4 to 12 demostrates that massive MIMO can deliver high throguhput in a Rician channel as presented by the table and the Spectral effeiciency (SE) plot.
References
| [1] | T. L. Marzetta, “Noncooperative Cellular Wireless with Unlimited Numbers of Base Station Antennas,” vol. 9, no. 11, pp. 3590–3600, 2010. |
| [2] | O. Idowu-bismark, F. Idachaba, and A. A. A. Atayero, “A Survey on Traffic Evacuation Techniques in Internet of Things Network Environment,” vol. 10, no. September, 2017. |
| [3] | O. Idowu-Bismark, F. Idachaba, and A. Atayero, “Massive MIMO Channel Characterization and Modeling: The Present and the Future,” Int. J. Appl. Eng. Res. ISSN, vol. 12, no. 23, pp. 973–4562, 2017. |
| [4] | O. B. Idowu-Bismark, A. E. Ibhaze, and A. A. Atayero, “Mimo Optimization Techniques and Their Application in Maximizing Throughput for 3GPP HSPA+,” J. Wirel. Netw. Commun., vol. 7, no. 1, pp. 1–8, 2017. |
| [5] | O. E. Agboje, O. B. Idowu-Bismark, and A. E. Ibhaze, “Comparative analysis of fast fourier transform and discrete wavelet transform based MIMO-OFDM,” Int. J. Commun. Antenna Propag., vol. 7, no. 2, 2017. |
| [6] | E. G. Larsson, “Massive MIMO for Next Generation Wireless Systems,” no. February, pp. 186–195, 2014. |
| [7] | F. Rusek, D. Persson, B. K. Lau, and E. G. Larsson, “Scaling up MIMO: Opportunities and Challenges with Very Large Arrays,” pp. 1–30. |
| [8] | S. Kumar, “Performance Analysis of Rayleigh and Rician Fading Channel Models using Matlab Simulation,” no. August, pp. 94–102, 2013. |
| [9] | L. Lu, S. Member, G. Y. Li, and A. L. Swindlehurst, “An Overview of Massive MIMO: Bene fi ts and Challenges,” vol. 8, no. 5, pp. 742–758, 2014. |
| [10] | S. Zhang, A. Doufexi, and A. Nix, “Evaluating Realistic Performance Gains of Massive Multi-User MIMO System in Urban City Deployments,” 2016. |
| [11] | J. Hoydis, B. Labs, and L. Sanguinetti, “Massive MIMO Networks: Spectral, Energy, and Hardware Efficiency,” 2017. |
| [12] | S. V Hanly, I. B. Collings, Z. A. Shaikh, and P. Whiting, “Law of Large Numbers Analysis of Antenna Selection aided Downlink Beamforming in Massive MISO under RF Chains Constraint,” pp. 163–168, 2016. |
| [13] | K. Zheng, S. Ou, and X. Yin, “Massive MIMO Channel Models: A Survey,” vol. 2014, 2014. |
| [14] | “Outage Performance of Cooperative Small-Cell Systems Under Rician Fading Channels.” |
| [15] | L. Sanguinetti, A. Kammoun, and M. Debbah, “Asymptotic Analysis of Multicell Massive MIMO over Rician Fading Channels.” |
| [16] | A. Abdi and G. B. Giannakis, “The Ricean,” vol. 2, no. 4, pp. 799–810, 2003. |
| [17] | E. Amador and P. Besnier, “L-UNIVERSITA ` TA ` MALTA Msida − Malta Msida − Malta,” no. April, 2011. |
| [18] | S. Kim and B. Shim, “FDD-Based Cell-Free Massive MIMO Systems,” p. 22. |
| [19] | O. Idowu-bismark, O. Kennedy, F. Idachaba, and A. A. Atayero, “A Primer on MIMO Detection Algorithms for 5G Communication Network,” vol. 8, no. June, pp. 194–205, 2018. |
| [20] | T. Van Chien and E. Björnson, Massive MIMO Communications. 2017. |



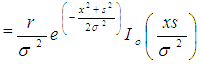


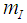 and mean of quadrature
and mean of quadrature 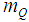 are given by
are given by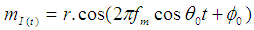
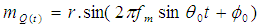
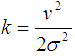
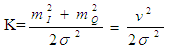
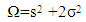
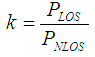
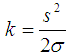
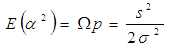
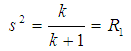
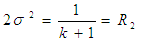
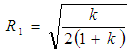
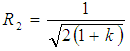
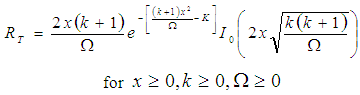

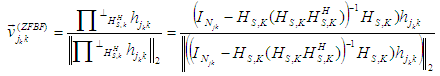
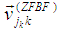 are generated by the projections of the channel vector
are generated by the projections of the channel vector 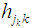 of the intended user on the orthogonal component of the space traversed by rows of channels of the intended users
of the intended user on the orthogonal component of the space traversed by rows of channels of the intended users 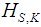 . (
. (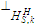 is the projection matrix unto the orthogonal complement of the column space) Since interference need to be cancelled for only active users, this is necessary for a scheduling set S.
is the projection matrix unto the orthogonal complement of the column space) Since interference need to be cancelled for only active users, this is necessary for a scheduling set S. 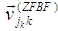 ,
,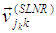 and
and 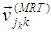 are the ZFBF, SLNR and MRT BF respectively [20].
are the ZFBF, SLNR and MRT BF respectively [20].








 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML
