N. M. El-Gohary1, M. A. M. El-Bendary2, F. E. Abd El-Samie3, M. M. Fouad1
1Department of Electonics and Communication, Faculty of Engineering, Zagazig University, Egypt
2Department of Communication Technology, Faculty of Industrial Education, Helwan University, Egypt
3Department of Electonics and Communication, Faculty of Electonics Engineering, Menofia University, Egypt
Correspondence to: N. M. El-Gohary, Department of Electonics and Communication, Faculty of Engineering, Zagazig University, Egypt.
| Email: |  |
Copyright © 2016 Scientific & Academic Publishing. All Rights Reserved.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/

Abstract
Reducing error in wireless, satellite, and space communication systems is critical. In the wireless communication system, various coding methods are employed on the data transferred to induce high bit error rates. High speed wireless networks, in order to address the large latency and degraded network throughput due to the retransmission triggered by frame loss, the purpose of this paper is to study and investigate the performance of fountain codes that is used to encode and decode the data stream in digital communication. This is an intelligent solution that encodes a number of redundant frames from the original frames upon link loss rate so that a receiver can effectively recover lost original frames without significant retransmissions. Since then, many digital Fountain coding methods have been invented such as Tornado codes, Luby transforms (LT) codes and Raptor codes.
Keywords:
Wireless communication systems,Fountain codes, Tornado codes, Luby transforms and Raptor codes
Cite this paper: N. M. El-Gohary, M. A. M. El-Bendary, F. E. Abd El-Samie, M. M. Fouad, Performance Evaluation of Various Erasures Coding Techniques in Digital Communication, Journal of Wireless Networking and Communications, Vol. 6 No. 1, 2016, pp. 10-20. doi: 10.5923/j.jwnc.20160601.02.
1. Introduction
In civil and military applications, wireless networking technologies have been widely deployed such as 3G/4G and IEEE 802.11 WLAN networks. However, wireless communication suffers from frame losses due to shadowing, mobility, channel fading, and interferences. Frame loss significantly undermines wireless network performance in that latency is enlarged and throughput is degraded. The large latency is induced by the retransmission of lost frames in the MAC layer [6].On the Internet, data is transmitted in the form of packets. Each packet is armed with a header that describes the source and the destination of the packet, and often also a sequence number describing the absolute or relative position of the packet in a given stream. These packets are routed in the network from the source to the destination [16]. Due to various reasons, for example, buffer overflows at the intermediate routers; some packets may get lost and never reach their destination, other packets may be announced as lost if the internal check of the packet does not match. Therefore, the Internet is a very good real-world pattern of the BEC.Reliable transmission of data over the Internet has been the subject of much research. Reliability is ensured by the use of suitable protocols. For example, the present TCP/IP ensures reliability by essentially retransmitting packets within a transmission window whose reception has not been acknowledged by the receiver. It is known that such protocols exhibit poor behavior in many cases, such as the transmission of data over heavily disabled channels or transmission of data from one server to multiple receivers or, such as poor wireless or satellite links. Moreover, ack-based protocols such as TCP perform poorly when the distance between the sender and the receiver is long, since large distances lead to idle times during which the sender waits for an acknowledgment and cannot send data. For these reasons, other transmission solutions have been proposed. One class of such solutions is based on coding. The original data is encoded using some linear erasure correcting code. If during the transmission some part of the data is lost, then it is possible to recover the lost data using erasure correcting algorithms. For applications it is critical that the codes used are able to correct as many erasures as possible, and it is also critical that the encoding and decoding algorithms for these codes are very fast. Reed–Solomon codes can be used to partially recover for the inefficiency of random codes. Reed–Solomon codes can be decoded from a block with the maximum possible number of erasures in time quadratic in the dimension. There are faster algorithms based on fast polynomial arithmetic, but these algorithms are often too complicated in practice. However, quadratic running times are still too large for many applications.Other codes are constructed with linear time encoding and decoding algorithms that can come arbitrarily close to the capacity of the BEC [16, 18]. These codes, called Tornado codes, are very similar to Gallager’s low-density parity-check (LDPC) codes [19], but they use a highly unequal weight distribution for the implied graphs.In computer networks, fountain codes are ideally suited for transmitting information. A server sending data to many recipients can perform Fountain code for a given piece of data to generate an infinite stream of packets. As soon as a receiver requests data, the packets are copied and forwarded to the receiver. In a broadcast transmission model, there is no need for copying the data since any outgoing packet is received by all the receivers. In other types of networks, the copying can be done actively by the sender, or it can be done by the network. An example, if multicast is enabled; the recipient collects the output symbols, and leaves the transmission as soon as it has been received by them. That time, it uses the decoding algorithm to recover the original symbols. That, the number is the same regardless of the channel characteristics between the sender and the receiver. More loss of symbols just translates to a longer waiting time to receive the packets. This paper surveys the channel coding methods in the physical layer and Digital Fountain code proposals in the application layer. The following paper is arranged as follows. Section 2 presents the RS codes architectures, applications and limitations. Section 3 discusses the fountain codes properties, the related erasure channel and construction. Section 4 Recent advances have produced powerful fountain codes, such as Tornado codes, Luby Transform (LT) codes and Raptor codes. Finally, section 5 discusses the advantages of fountain code over Reed Solomon code. Finally section 6 presents the conclusion.
2. Developing Background Related Work and Motivations
2.1. Error Correction Control (ECC)
In information and coding theory with applications in computer science and telecommunication system, error detection and correction are techniques that enables reliable and efficient delivery of digital data over communication channels. Many communication channels are subject to channel noise, and thus errors may be inserted during transmission from the source to a receiver. Error detection techniques permit detecting such errors, while error correction enables regeneration of the original data in many cases.Error correction control is accomplished by adding redundant symbols to the message. These redundant symbols make it possible for the receiver to detect and /or correct some of the errors that may occur in the received message. The main challenge is to ensure the required protection against the determined transmission errors without paying too high a price in adding extra symbols. Error correction may generally be accomplished in two different ways:• Forward error correction (FEC): The sender encodes the data using an error-correcting code (ECC) before transmission. The receiver used the additional redundancy added the code to recover the original data. • Automatic repeat request (ARQ): (referred also to as backward error correction): Every block of data received is checked using the error detection code used, and if the check fails, retransmission of the data is requested – this may be done repeatedly, until the data can be executed. This is an error control technique whereby an error detection scheme is combined with requests for retransmission of incorrect data. FEC and ARQ may be combined, this is called hybrid automatic repeat-request (HARQ), such that minor errors are corrected without retransmission, and major errors are corrected via a request for retransmission. There are many different families of error-correcting codes of major importance for recording applications is the family of Reed-Solomon (RS) codes.
2.2. Binary Erasure Channel
The Binary Erasure Channel (BEC) is a channel model where the receiver either receives the transmitted bit or is informed with the erasure of the bit, that is, the bit was not received or erased. Therefore, the receiver has no idea about the transmitted bit with a certain probability p, and is exactly sure about the transmitted bit with a certain probability 1-p. According to Shannon, the capacity of BEC is 1-p, which means that for the alphabet size of 2k, where k is the number of bits in the alphabet, no more than (1− p) k bits/symbol can be reliably communicated over the binary erasure channel [20].Feedback from the receiver to the transmitter will not increase the capacity of the channel and reliable communication should be possible at this rate. Automatic Repeat Request (ARQ) schemes have so long been used as a classical approach to solve the reliable communication problem. However, redundant number of feedbacks used in the case of erasures causes improvident usage of bandwidth, network overloads and impossible delays. Also known as rateless erasure codes are a class of erasure codes with the property that a potentially limitless sequence of encoding symbols can be generated from a given set of source symbols such that the original source symbols can ideally be recovered from any subset of the encoding symbols of size equal to or only slightly larger than the number of source symbols. The term fountain or rateless refers to the fact that these codes do not exhibit a fixed code rate.
2.3. Reed-Solomon Code
Reed-Solomon (RS) code is a forward error-correcting code first invented in 1960 by Irving Reed and Solomon [1]. Only in the past few years has it become computationally possible to send high-bandwidth data using RS. Versions of Reed-Solomon codes are now used in error-correction systems found just about everywhere, including the storage devices, wireless communications, satellite communications and digital television.RS codes are non-binary cyclic error-correcting codes. The RS encoder takes a block of digital data and adds extra information to the original data. While the errors occur during transmission or storage, the RS decoder processes, each block and attempts to correct errors and recover the original data. The number and type of errors that can be corrected depends on the characteristics of the RS code.
2.3.1. Encoding RS Codes
The basic structure of RS code is represented in Fig(1), as shown in that the codeword symbols (n) is unite of two segments information symbols (k) and parity symbols (2t). The information symbols (k) are having a message that is to be transmitted and parity symbols (2t) is the redundancy added to message to transmit it from source to destination without error [7].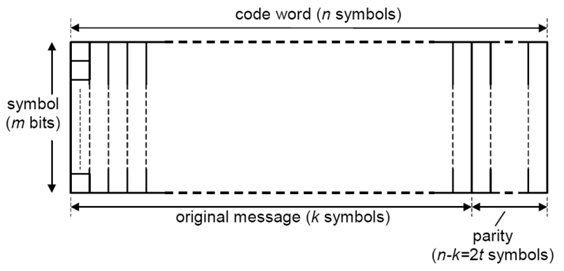 | Figure 1. Encoding of RS codes |
Reed-Solomon codes are nonbinary cyclic codes with symbols made up of m-bit sequences, where m is any positive integer having a value greater than 2. An RS code is specified as an RS (n, k) codes on m-bit 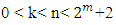 | (1) |
Where k is the number of data symbols being encoded, and n is the total number of code symbols in the encoded block. For the most conventional R-S (n, k) code,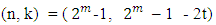 | (2) |
Where t is the symbol-error correcting capability of the code, and n - k = 2t is the number of parity symbols. An extended R-S code can be made up with 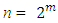 or
or  + 1. Reed-Solomon codes attain the largest possible code minimum distance for any linear code with the same encoder input and output block lengths. For nonbinary codes, the distance between two code words is defined as the number of symbols in which the sequences differ. For Reed- Solomon codes, the code minimum distance is given by:
+ 1. Reed-Solomon codes attain the largest possible code minimum distance for any linear code with the same encoder input and output block lengths. For nonbinary codes, the distance between two code words is defined as the number of symbols in which the sequences differ. For Reed- Solomon codes, the code minimum distance is given by: 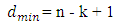 | (3) |
The code is capable of correcting any combination of t or fewer errors, where t can be expressed as [3]: | (4) |
RS differs from a Hamming code in that it encodes groups of bits instead of one bit at a time. Classical coding scheme for recovering erasures are Reed-Solomon codes [1, 3] employed in a variety of commercial applications, most notably in data storage as a key component of compact disks. In coding theory, Reed-Solomon codes are an example of Maximum Distance Separable (MDS) codes which achieve the Singleton bound [4]. The maximum distance separable (MDS) codes are practical codes that achieve the capacity of the erasure channel. A (n, k, d) MDS code, has a property that any k coordinates constitute an information set [2]. A receiver that receives any k symbols from a total of n symbols in each codeword can reconstruct the original message, provided it knows the position of the k received symbols. Reed Solomon (RS) codes are the most well-known MDS codes. These can be decoded in time O (K2), using algebraic methods such as list decoding.
2.3.2. Decoding of RS Codes
The RS decoder consists of two main stages; (1) error detection stage, and (2) error correction stage as shown in Fig. (2) [15]. Firstly, a serial syndrome is used to check if this codeword is a valid codeword or not. If errors occurred during transmission, the decoder carried out error detection, then try to correct these errors. Secondly, the key equation solver is used as decoding algorithm to find the coefficients of the error-location polynomial σ(x) and error-evaluator polynomial W(x). Thirdly, the Chien search block which is used to find the roots of σ(x) which present the inverse of the error locations. Fourthly, the Forney algorithm block is used to find the values of the errors. Finally, after getting the values and locations of the error, the received codeword can be corrected by XOR-ing the received vector with the error vector.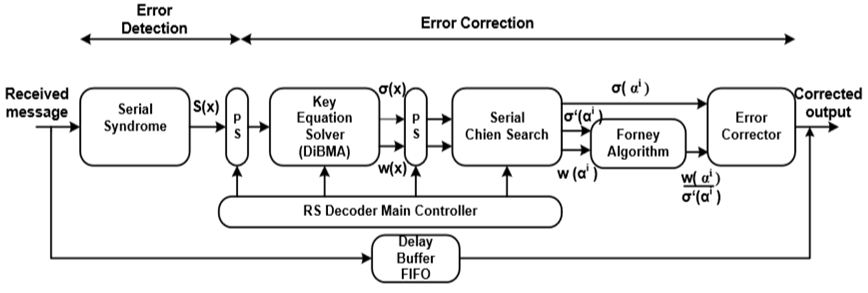 | Figure 2. RS decoder |
2.3.3. Reed-Solomon Code Applications
Reed-Solomon codes are the most frequently used digital error control codes in the world, due their usage in computer memory and non-volatile memory applications. A hurried list of significant applications includes the Digital Audio Disk, Deep Space Telecommunication Systems, and Error Control for Systems with Feedback, Spread-Spectrum Systems, and Computer Memory [8].
2.3.4. Reed-Solomon Codes Limitations
RS codes are not proper for bulk data distribution over the internet although spreading. When data rates are of the order of Mbps, the quadratic decoding time is unacceptable [2]. Moreover, typical RS code implementations have small block lengths such as the NASA standard (255; 233; 33) code. This requires a large file to be divided into many small blocks before transmission. Finally, since RS codes are block codes, they need to be designed for a specific rate. This requires that we need previous to evaluate the erasure probability of the channel. It is not possible when multiple clients over different quality of channels are being served simultaneously.
3. Fountain Codes
A fountain code is a forward-error-control code that can produce as many redundant packets as needed for packet erasure correction. Unlike automatic-repeat-request (ARQ) transmission, fountain coding does not require the destination to inform the source of the identities of the packets that are erased or even keep track of which packets are erased. We discuss the use of fountain coding for both unicast and multicast transmission in packet radio systems, where communication occurs over time-varying channels with fading, shadowing, and other types of propagation losses.A decoding algorithm for a Fountain code is an algorithm which can recover the original k input symbols from any set of n output symbols with high probability [16]. For good Fountain codes the value of n is very close to k, Note that the number n is the same regardless of the channel characteristics between the sender and the receiver. More loss of symbols just translates to a longer waiting time to receive the n packets. For noisy wireless channels, the waiting time and then the overall throughput performance of the fountain coding system depend heavily on the selection of the channel code and the modulation format used to transmit the wireless signals. Proposed for wireless mesh networks by Katti, et al not only forwards the packets, but also mixes packets from different sources into a single transmission and resolves the packets at the receiver. In upper layers, a coding concept called Digital Fountain has been introduced in 1998 by Byers, et al to generate a stream of packets including some redundant packets, like in a water fountain to address the potential packet loss in multicast applications that do not allow retransmission. Since then, many Digital Fountain coding methods have been invented such as Luby transform coding and Raptor codes.Consider a setting where a large file is disseminated to a wide audience who may want to access it at various times and have transmission links of different quality. Current networks use unicast established protocols such as the transport control protocol (TCP), which requires a transmitter to continually send the same packet until acknowledged by the receiver. It can easily be seen that this architecture does not scale well when many users access a server concurrently and is extremely inefficient when the information transmitted is always the same. In fact, TCP and other unicast protocols place strong importance on the ordering of packets to simplify coding at the expense of increased traffic.
3.1. Digital Fountain Codes
The digital fountain was devised as the ideal protocol for transmission of a single file to many users who may have different access times and channel fidelity. The name is drawn from an analogy to water fountains, where many can fill their cups with water at any time. The output Packets of digital fountains must be universal like drops of water and hence be useful independent of time or the state of a user’s channel [12, 13].The encoder of fountain codes is like a fountain spewing as show in Fig (3). Infinite coded symbols can be produced. Source data is divided into k input symbols of size l. With fountain codes, the k input symbols are combined into infinite encoding symbols at source. All k input symbols can be cured from any set of (1+ε) k encoding symbols, where 0< ε <1. Encoder of fountain codes is bit rate independent which is not limited by the size of the source data and can generate an unlimited number of encoding symbols.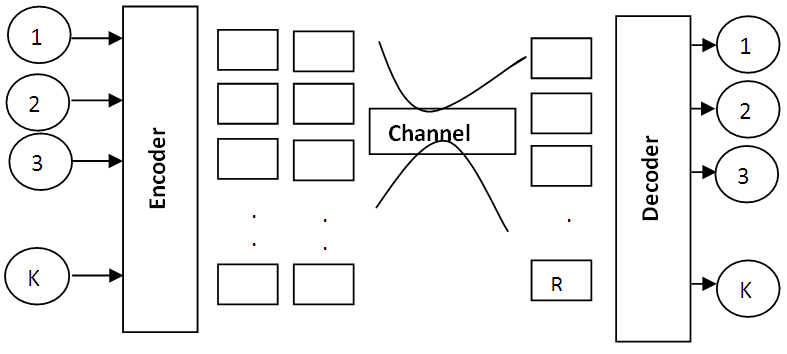 | Figure 3. Fountain code |
3.2. Fountain Codes Properties
Consider a file that can be split into k packets or information symbols and must be encoded for a BEC. A digital fountain that transmits this file has the next properties:1. It can generate an endless supply of encoding packets with constant encoding cost per packet in terms of time or arithmetic operations.2. A user can reconstruct the file using any k packets with constant decoding cost per packet, meaning the decoding is linear in k.3. The space needed to store any data during encoding and decoding is linear in k.These properties show that the digital fountains are as reliable and efficient as TCP systems, but also universal and tolerant, properties desired in networks.
3.3. Fountain Code Construction Outline
Fountain Codes are a new class of codes designed and ideally suitable for dependable transmission of data through an erasure channel with unknown erasure probability. Infinite number of output symbols can be produced potentially by the encoder. Output symbols can be bits or more general bit sequences. However, random linear Fountain Codes have encoding complexity of 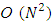 and decoding complexity of
and decoding complexity of 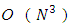 which makes them impractical for nowadays applications.The fountain code constructions we provide all have the property that encoded symbols are generated separately from one another. Moreover, we will assume that the set of receiving encoded symbols is independent of the values of the encoded symbols in that set, an assumption that is often true in practice. For a given value of k, these assumptions mean that the probability of the inability of the decoding is only dependent on how many encoded symbols are received and independent of the pattern of which encoded symbols are received.
which makes them impractical for nowadays applications.The fountain code constructions we provide all have the property that encoded symbols are generated separately from one another. Moreover, we will assume that the set of receiving encoded symbols is independent of the values of the encoded symbols in that set, an assumption that is often true in practice. For a given value of k, these assumptions mean that the probability of the inability of the decoding is only dependent on how many encoded symbols are received and independent of the pattern of which encoded symbols are received.
3.3.1. Fountain Coding
If the original k source symbols can be recovered from any k encoding symbols, fountain code is maximized. Fountain codes are known that have efficient encoding and decoding algorithms and that permit to pick up the original k source symbols from any k’ of the encoding symbols with high probability, where k’ is just slightly larger than k.Digital fountains have changed the standard transmission model. A digital fountain can encode and transmit an infinite number of data packets until every user has enough information to ensure correct decoding. Emerging peer-to-peer applications in multimedia broadcasting are only two examples of many other scripts where digital fountains can be applied successfully.Consider a file that can be split into k packets or information symbols and must be encoded for a BEC as shown in Fig (4) [17]. Regardless of the erasure probability, Fountain Codes are near optimal for all BEC. Therefore, on the BEC, Fountain Codes are called universal codes. A message consists of k*k bits and each drop contains k bits.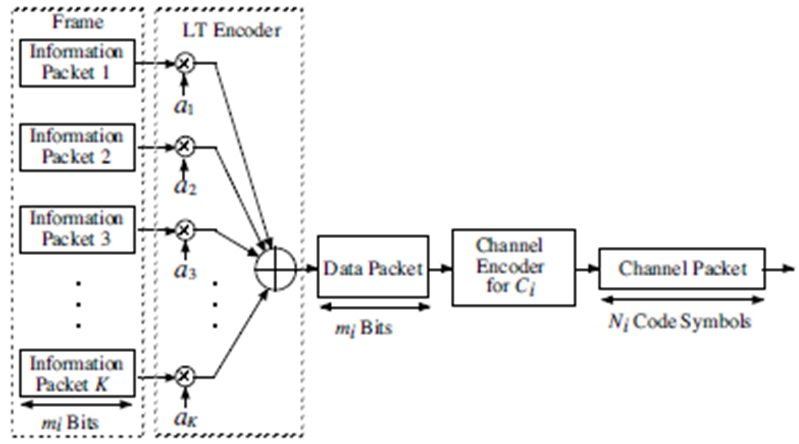 | Figure 4. Fountain code |
Whoever collects any K' ≥ K number of k bits, where K ' is little larger than K, can recover the original message with high probability.Fountain Codes can be accomplished at random with an average degree of k / 2. The degree is the number of one's divided by the total number of bits in the generator matrix. The average degree of the generator matrix determines the complexity of encoding and decoding process. The higher the degree, the higher the complexity at the transmitter and receiver side and the more successful the receiver is in the decoding phase. Let us assume that we transmit k source symbols k s, s, s... s 1 2 3 with a random generator matrix of degree k / 2. The encoding process of Fountain Codes is given by the following equation [9]: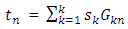 | (5) |
Where 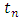 indicates to the transmitted symbols.
indicates to the transmitted symbols. 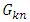 Can be generated at the transmitter side pseudo-randomly with a random seed, namely by a key, and transmitted to the receiver causing an extra overhead cost. Therefore, the symbol size is much larger than the key size, this overhead is neglectable. One other way to produce a unique
Can be generated at the transmitter side pseudo-randomly with a random seed, namely by a key, and transmitted to the receiver causing an extra overhead cost. Therefore, the symbol size is much larger than the key size, this overhead is neglectable. One other way to produce a unique  is to synchronize the receiver and the transmitter with same clock pulses and to use deterministic random number generators on both sides.
is to synchronize the receiver and the transmitter with same clock pulses and to use deterministic random number generators on both sides.
3.3.2. Fountain Decoding
The decoding process of Fountain Codes is given as: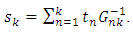 | (6) |
In order for a k*k G matrix to be invertible, each row should be linearly independent from the others. The probability that the first row is not an all zero row is 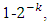 the probability that the second row is neither all zero nor same with the first row is
the probability that the second row is neither all zero nor same with the first row is 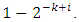 Iterating until K, we get as the overall success rate:
Iterating until K, we get as the overall success rate: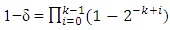 | (7) |
1−δ is lower bounded by 0.289 for k > 10. For any NxK binary matrix to be invertible, 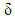 is upper bounded by
is upper bounded by 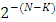 . Accordingly, each additional row increases the success probability drastically. Thus, as the message size increases, random Fountain Codes come arbitrarily close to the channel capacity. Despite a very small overhead and rate erasure independency, random Fountain Codes have a quadratic encoding complexity, k bits times the degree k/2, and cubic decoding complexity
. Accordingly, each additional row increases the success probability drastically. Thus, as the message size increases, random Fountain Codes come arbitrarily close to the channel capacity. Despite a very small overhead and rate erasure independency, random Fountain Codes have a quadratic encoding complexity, k bits times the degree k/2, and cubic decoding complexity 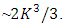 This makes them far away from most of the applications such as mobile broadcasting, where only a limited processor power can be used on the receiver side.Then, many digital Fountain coding methods have been invented such as Tornado codes, Luby transform codes and Raptor codes.
This makes them far away from most of the applications such as mobile broadcasting, where only a limited processor power can be used on the receiver side.Then, many digital Fountain coding methods have been invented such as Tornado codes, Luby transform codes and Raptor codes.
4. Fountain Coding Methods
4.1. Tornado Code
4.1.1. Introduction
Tornado codes first appeared in a technical report in 1997. Tornado codes are a new class of erasure randomized codes which have linear-time encoding and decoding algorithms. They can be used to transmit over erasure channels at rates extremely close to capacity. For Tornado codes, the encoding and decoding algorithms are both simple and faster by orders of magnitude than the best software implementations of standard erasure codes. Tornado codes will be expected extremely useful for applications such as reliable distributions of bulk data, including video distribution, software distribution, news and financial distribution, popular web site access, and military communications.We consider a system model in which a single transmitter performs evaluated data transfer to a larger number of users on an erasure channel. Our objective is to achieve complete file transfer with the minimum number of encoding symbols and low decoding complexity. For k information symbols, RS codes can achieve this with k log k encoding and quadratic decoding times. The reason for the longer decoding time is that on RS codes, every redundant symbol depends on all information symbols. In Tornado codes by contrast, every redundant symbol depends only on a small number of information symbols. Thus they achieve linear encoding and decoding complexity, with the cost that the user requires slightly more than k packets to successfully decode the transmitted symbols. The main contribution is the design and analysis of optimal degree distributions for the bipartite graph such that the receiver is able to recover all missing bits by a simple erasure decoding algorithm. The innovation of Tornado code has also inspired work on irregular LDPC codes.
4.1.2. Construction
The design and analysis of Tornado codes are mathematically simple and interesting. The design requires careful choice of a random irregular bipartite graph where the structure of the irregular graph is very important. The progress of the decoding algorithm is designed by a simple AND-OR tree analysis, which instantly gives rise to a polynomial in one variable with coefficients determined by the graph structure. We design a graph structure based on these polynomials assure successful decoding with high probability.Tornado codes are erasure block codes based on the irregular spare graph. Given an erasure channel with loss probability p, they can correct up to p (1- ε) errors. They can be encoded and decoded in time proportional to n*log (1/ ε). There are eight input symbols named x1, x2… x8 as shown in Fig (5). With tornado codes, four encoding symbols named y1, y2, y3 and y4 is produced by eight input symbols. Tornado codes can support that any one of y1, y2, y3 and y4 can be recovered by three others. 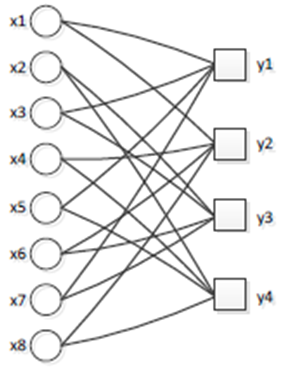 | Figure 5. Tornado codes |
Tornado codes are not suitable for large data transfer systems because the complexity of encoding and decoding algorithms for tornado codes is proportional to block length. For encoding the large amounts of data, an alternative classical ARQ concept is used as on the Internet.
4.2. LT Code
4.2.1. Introduction
LT codes are the first implementation of digital fountain codes in 2002 proposed by Michael Luby. Luby Transform (LT) codes have been invented to reduce the encoding and decoding complexity of random linear Fountain Codes while the small overhead is ensured. With a good choice of degree distributions of the edges in the Tanner graph, LT codes randomly close to channel capacity with certain decoder reliability and logarithmically inducing increases in encoding and decoding costs. In LT codes, Data was divided into blocks with fixed size. Each block is divided into fixed size symbols. So the number of input symbols is fixed. The encoder of LT codes can generate an infinite number of encoded symbols. When the number of encoding symbols is received slightly larger than the number of input symbols, this means the decoder of LT codes can recover all input symbols.Reducing the degree distribution resulting linear time encoding and decoding complexity leads to decrease in the reliability of the decoder. Thus, the decoder cannot decode all the input symbols with the lower degree distribution for the same overhead limitation. So, correcting the erasures arising from the weakened decoder would utilize an erasure correcting pre-code.
4.2.2. The Construction
For the binary erasure channel, LT codes are considered the first practical rateless codes. The encoder can produce as many encoding symbols as required to decode k information symbols. For LT codes, the encoding and decoding algorithms are simple and similar to parity-check processes. LT codes are efficient in that the transmitter does not require an acknowledgement (ACK) from the receiver. This property is especially desired in multicast channels because it will significantly decrease the overhead incurred by processing the ACKs from multiple receivers.LT codes are known to be efficient if k information symbols can be recovered from any 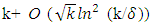 encoding symbols with probability
encoding symbols with probability  using
using 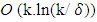 operations. However, their bit error rates cannot be decreased below some lower bound, meaning they suffer an error floor.To reduce the computational complexity, the number of edges at the encoder side should be reduced. LT codes with simple encoding and decoding algorithms can then be considered as sparse random linear Fountain Codes. Although, there are simple and fixed encoding and decoding schemes defined for LT codes the degree distributions of the edges play a crucial role in the design of good codes. Good codes are such codes, which have low encoding and decoding costs as well as a small overhead and a decoding failure. Let us start with the definitions of encoding and decoding schemes.A. LT CodingAny number of encoding symbols can be independently generated from k information symbols by the following encoding process:1) Determine the degree d of an encoding symbol. The degree is chosen at random from a given node degree distribution P (x).2) Choose d distinct information symbols uniformly at random. They will be neighbors of the encoding symbol.3) Assign the XOR of the chosen d information symbols to the encoding symbol. This process is similar to generating parity bits except that only the parity bits are transmitted.The degree distribution P (x) in Fig(6), comes from the sense that we can draw a bipartite graph, in which consists of information symbols as variable nodes and encoding symbols as factor nodes. The degree distribution determines the performance of LT codes, such as the number of encoding symbols and probability of successful decoding. The degree distribution is analyzed.
operations. However, their bit error rates cannot be decreased below some lower bound, meaning they suffer an error floor.To reduce the computational complexity, the number of edges at the encoder side should be reduced. LT codes with simple encoding and decoding algorithms can then be considered as sparse random linear Fountain Codes. Although, there are simple and fixed encoding and decoding schemes defined for LT codes the degree distributions of the edges play a crucial role in the design of good codes. Good codes are such codes, which have low encoding and decoding costs as well as a small overhead and a decoding failure. Let us start with the definitions of encoding and decoding schemes.A. LT CodingAny number of encoding symbols can be independently generated from k information symbols by the following encoding process:1) Determine the degree d of an encoding symbol. The degree is chosen at random from a given node degree distribution P (x).2) Choose d distinct information symbols uniformly at random. They will be neighbors of the encoding symbol.3) Assign the XOR of the chosen d information symbols to the encoding symbol. This process is similar to generating parity bits except that only the parity bits are transmitted.The degree distribution P (x) in Fig(6), comes from the sense that we can draw a bipartite graph, in which consists of information symbols as variable nodes and encoding symbols as factor nodes. The degree distribution determines the performance of LT codes, such as the number of encoding symbols and probability of successful decoding. The degree distribution is analyzed.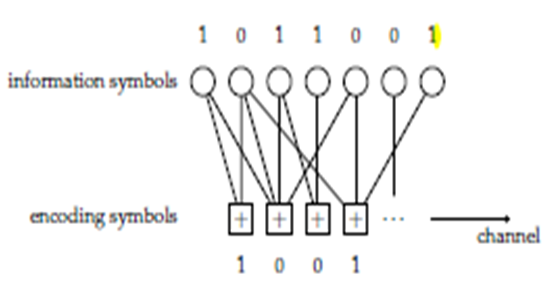 | Figure 6. Generation of encoding symbols |
The encoding symbols are transmitted through a BEC with the probability of erasure p. The special characteristic of a BEC is that receivers have correct data or no data. There is no confusion where the decoder needs to “guess” the original data; it recovers the true data or gives up.B. LT DecodingFor decoding of LT codes, a decoder needs to know the neighbors of each encoding symbol. This information can be transferred in several ways. For example, a transmitter can send a packet, which consists of an encoding symbol and the list of its neighbors. There is an alternative method is the encoder and the decoder share a random number generator seed, and the decoder finds out the neighbors of each encoding symbol by generating random linear combinations synchronized with the encoder.
4.2.3. Degree Distribution
LT codes do not have a fixed rate and hence the desired property is that the probability of successful recovery is as high as possible while the number of encoding symbols required is kept small. Describing the property in the terminology of the LT process:• For encoding symbols, the release rate is low in order to keep the size of the ripple small and prevent waste of encoding symbols.• For encoding symbols, the release rate is high enough to keep the ripple from dying out.Therefore, the degree distribution of encoding symbols needs to be very well designed so as to balance between the trade-off. This is the reason that the degree distribution plays an important role in LT codes. Several probability distributions are investigated as the degree distribution used in the fame Fountain encoding process [10] as follows:1) Uniform distribution: 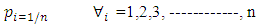 | (8) |
2) Normal distribution:  | (9) |
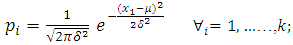 | (10) |
Where 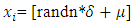 3) Sequential distribution:
3) Sequential distribution: | (11) |
4) Ideal solution distribution 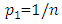 | (12) |
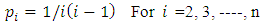 | (13) |
5) Robust Soliton distribution, 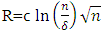 where c and
where c and 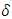 are extra parameters; c > 0 is some suitable constant.
are extra parameters; c > 0 is some suitable constant. 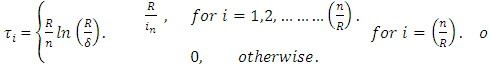 | (14) |
Enough frames can be encoded together as redundant frames to make sure there are enough variety of encoded frames at the receiver.
4.3. Raptor Code
4.3.1. Introduction
Raptor code has been standardized in the 3GPP (Third Generation Partnership Project). Raptor Codes are an extension of LT codes combined with a pre-coding scheme. Raptor (rapid Tornado) codes were developed and patented in 2001 as a way to reduce decoding cost to O (1) by preprocessing the LT code with a standard erasure block code (as a Tornado code). The main idea of Raptor Codes is to refresh the condition of recovering all input symbols and to require that only a constant fraction of input symbols be recoverable. Then the number of edges in the Tanner graph will exhibit only a constant degree which will precede linear time encoding and decoding costs. This is done by utilizing an erasure correcting pre-code working in linear time. The degree distribution, which is used for Raptor Codes, should be completely different from the one that of LT codes. Because, in the concept of Raptor Codes, we are forced to recover as many input symbols as possible for a given constant average degree rather than to recover all input symbols to be recovered and decoding to be successful. Degree distribution design and pre-coding is the heart of Raptor Codes. The degree distribution, which is used for Raptor Codes, should be completely different from the one that of LT codes. From the concept of Raptor Codes, we are forced to recover as many input symbols as possible for a given constant average degree rather than to recover all input symbols while maintaining the small overhead.
4.3.2. The Construction
Digital Fountain, Inc. proposed Raptor codes in 2006. It is a concatenation of a systematic pre-code with LT codes. As shown in Fig (7), in the pre-code, k native symbols are first mapped to (1+ε) k pre-coded symbols. Infinite coded symbols can be generated from pre-coded symbols by LT codes. In decoding process of Raptor codes, pre-coded symbols are recovered by LT codes firstly, and then input symbols are recovered by pre-coded symbols.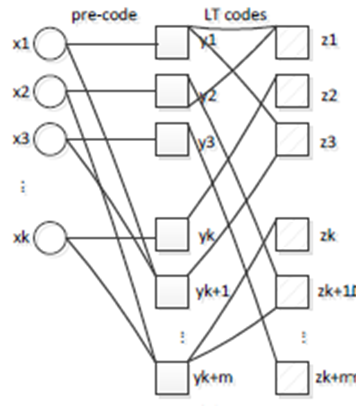 | Figure 7. Raptor codes |
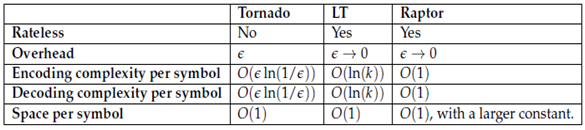
A Raptor code can achieve constant per-symbol encoding and decoding cost with overhead close to zero and a space proportional to k. This has been shown to be the closest code to the ideal universal digital fountain. A similar vein of work was proposed in under the name online codes. We have already seen two extreme cases of Raptor codes. When there is no pre-code, then we have the LT code. As an example of a pre-code only (PCO) Raptor code for the s are an extension of LT codes [11].Raptor Codes can produce a potentially infinite stream of symbols such that any subset of symbols of size k (1+ε) is sufficient to recover the original k symbols with high probability. The original symbols are recovered from the collected ones with O (k log (1/ε)) operations and output symbol is generated using O (log (1/ε)) operations. Raptor encoding starts with a suitable design of the pre-code. Shokrollahi uses LDPC codes as a pre-code with a constant rate of (1+ε /2) (1+ε) and BP algorithm can work in linear time and decode (ε / 4) (1+ε) fraction of erasures where ε is a real positive number. Next, the intermediate symbols are encoded with LT coding using a suitable degree distribution.Raptor decoding starts with the LT decoding process. In the example, LT decoding can recover all the intermediate symbols, but the ones filled with black. Since the pre-code is systematic, the first three input symbols are immediately recovered. The fifth intermediate symbol is encoded by xor-ing the third and fourth input symbol. We can recover the fourth input symbol by adding the fifth intermediate symbol to the third input symbol. Hence, as it is seen that the decoding process succeeds. Decoding is done the same way as described in this paper for LT decoding. LDPC decoding is performed using the BP algorithm.The table below summarizes the characteristics of the various codes that are designed for the digital fountain ideal:Table 1. Summary of fountain codes
 |
| |
|
5. Advantages of Fountain Code over Reed Solomon Code
• A DF Raptor code with k input symbols that produces n output symbols using symbols of size S bytes is designated Raptor (n,k,S).The Digital fountain code does not have any limitation to the amount of data that can be protected: the number of source symbols k for a DF Raptor code can be as large as desired, and the symbol size S is not subject to any constraints other than that it be less than or equal to the packet size. As a result, the value of S can be much smaller for a DF Raptor code than is possible for a Reed-Solomon erasure code.• A DF Raptor code’s processing requirements are significantly less than that of a Reed-Solomon erasure code and grow only linearly with the source block size, while a Reed-Solomon erasure code’s processing requirements grow quadratically with source block size.• In streaming applications, the erasure correction performance of Reed-Solomon erasure codes is directly affected by the inefficiencies associated with the limited number of symbols that can be used by the Reed-Solomon algorithm, while Reed-Solomon erasure codes can require an order of magnitude greater processing power for encoding and decoding than a DF Raptor code.• The Digital Fountain code's offer excellent performance compared to the Reed-Solomon erasure codes. For a given rate of packet loss, the mean time between artifacts for the DF Raptor code is significantly greater than that of the Reed-Solomon codes As can be seen from Fig (8).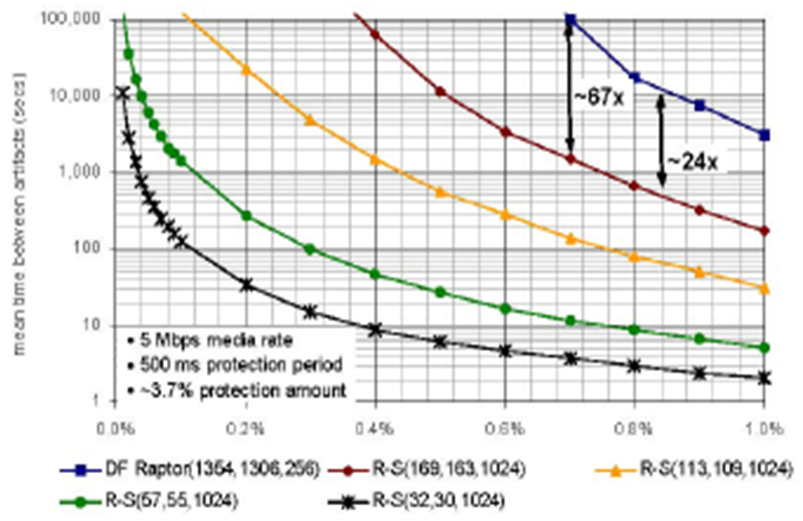 | Figure 8. A DF Raptor code can provide a mean time than that provided by Reed-Solomon erasure codes [21] |
• In streaming applications, the length of the protection period reflects a trade-off between robustness and latency. In general, the longer the protection period, the more likely that the actual number of lost packets over that period will approach the average packet loss rate so that a fixed code rate erasure correction code can be sure to provide sufficient protection. The DF Raptor code provides greater protection against packet loss, one can arbitrarily choose any protection period and latency without constraint as shown in Fig (9). The Reed-Solomon erasure code with the same amount of overhead and with the same mean time between artifacts, the protection period that can be supported by a single Reed-Solomon code is limited. With Reed-Solomon codes, however, a protection period of data must be segmented into multiple blocks that are protected individually, and the resulting encoded blocks are then interleaved, at the cost of additional processing as well as reduced packet loss protection.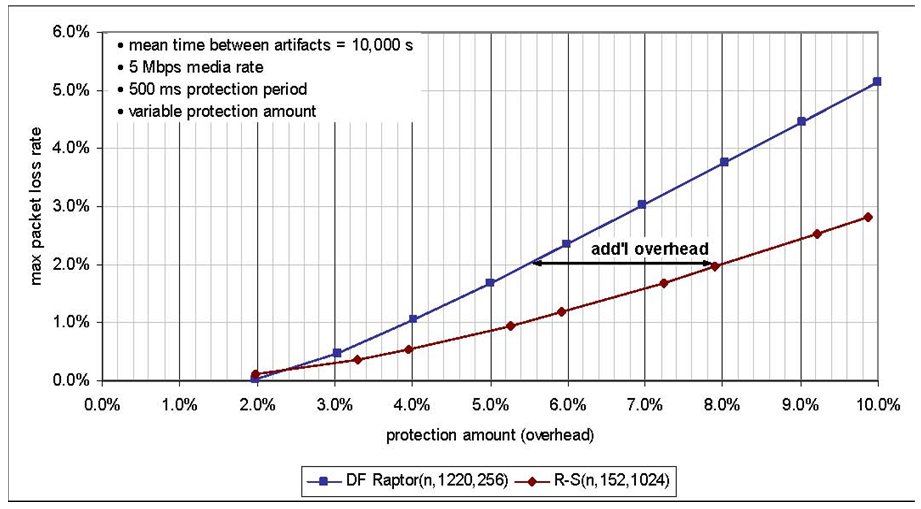 | Figure 9. The maximum packet loss rate for the DF Raptor code is higher than for the Reed-Solomon code [21] |
6. The Conclusions
It is clear, that the Fountain codes have flexible applications at a fixed code rate cannot be determined previously, and where efficient encoding and decoding of large amounts of data is required as:1) When multiple clients over different quality of channels are being served simultaneously. 2) The decoding time is acceptable when data rates are of the order of Mbps. 3) Fountain codes are suitable for large data distribution over the internet.4) Raptor Q code, is the more advanced Raptor code with greater flexibility and improved reception overhead. This code has been introduced into the IETF. It can be used with up to 56,403 source symbols in a source block, and a total of up to 16,777,216 encoded symbols produced for a source block. This code is able to recover a source block from any collection of encoded symbols equal to the number of source symbols in the source block with high probability and seldom cases from slightly more than the number of source symbols in the source block.
References
| [1] | I. S. Reed and G. Solomon “Reed-Solomon code”. Polynomial codes over certain _nite _elds. Journal of the Society for Industrial and Applied Mathematics, 1960. |
| [2] | David Forney Jr., Unpublished Course notes., http://ssg.mit.edu/6.451, 2003. |
| [3] | S. Wicker and V. Bhargava, Eds., “Reed-Solomon Codes and Their Applications” IEEE Press, Piscataway, NJ, USA, 1994. |
| [4] | J. van Lint, “Introduction to Coding Theory” Springer-Verlag (2nd Ed.), 1992. |
| [5] | G. Joshi, J .Bum Rhim, John Sun, Da Wang, “Fountain codes”, December 7, 2010. |
| [6] | Qingmei Yao, Chong Tang, Shaoen Wu Frame Fountain: Coding and Decoding MAC Frames. |
| [7] | International Journal of Advances in Science and Technology, BER Performance of Reed-Solomon Code Using M-ary FSK Modulation in AWGN Channel Vol. 3, No.1, 2011. |
| [8] | V. Korrapati, M V D Prasad*2, D. Venkatesh, G. Arun Tej “A Study on performance evaluation of Reed Solomon Codes through an AWGN Channel model for an efficient Communication System” International Journal of Engineering Trends and Technology (IJETT) - Volume4Issue4- April 2013. |
| [9] | G. GÜL, S. Adhikari and E. Mustafin “Fountain Codes, LT Codes, and Raptor Codes”. |
| [10] | Q. Yao, C. Tang, Sh. Wu School of Computing University of Southern Mississippi, USA “Frame Fountain: Coding and Decoding MAC Frames”. |
| [11] | A. Shokrollahi and M. Luby Foundations and Trends in Communications and Information Theory “Raptor Codes” Vol. 6, Nos. 3–4 (2009) 213–322 _c 2011. |
| [12] | J. Byers, M. Luby, M. Mitzenmacher, and A. Rege, “A Digital Fountain Approach to Reliable Distribution of Bulk Data,” In Proceeding of SIGCOMM, Vancouver, BC, CA, September 1998. |
| [13] | J. Liao, L. Zhang, X. Zhu, J. Wang and M. Liao “ Loss Rate Based Fountain Codes for Data Transfer”. |
| [14] | A. Khisti “Tornado Codes and Luby Transform Codes” October 22, 2003. |
| [15] | H. A. A. Elsaid, “Design and implementation of Reed-Solomon decoder using decomposed inversion less Berlekamp-Massey algorithm”, M. Sc. Thesis, Faculty of Engineering, Cairo University, 2010. |
| [16] | A. Shokrollahi, \Raptor codes," IEEE Transactions on Information Theory, vol.52, no. 6, pp. 2551{2567, June 2006. |
| [17] | J. D. Ellis, “Adaptive Transmission Protocols For Wirless Communication Systems With Fountain Coding” A Dissertation Presented to the raduate School of Clemson University, December 2013. |
| [18] | M. Luby, M. Mitzenmacher, A. Shokrollahi, and D. Spielman, “Efficient erasure correcting codes,” IEEE Trans. Inf. Theory, vol. 47, no. 2, pp. 569–584, Feb. 2001. |
| [19] | R. G. Gallager, “Low Density Parity-Check Codes”. Cambridge, MA: MIT Press, 1963. |
| [20] | D. J.C. MacKay Cavendish Laboratory, University of Cambridge“ Fountain codes” 1998 IEE, Cagliari, Italy Proc. of the Fourth Workshop on Discrete Event Systems. |
| [21] | San Diego "Why DF Raptor is Better Than Reed-Solomon for Streaming Applications", U.S. Dept. of Commerce, 2010. |




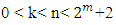
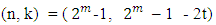
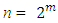 or
or  + 1. Reed-Solomon codes attain the largest possible code minimum distance for any linear code with the same encoder input and output block lengths. For nonbinary codes, the distance between two code words is defined as the number of symbols in which the sequences differ. For Reed- Solomon codes, the code minimum distance is given by:
+ 1. Reed-Solomon codes attain the largest possible code minimum distance for any linear code with the same encoder input and output block lengths. For nonbinary codes, the distance between two code words is defined as the number of symbols in which the sequences differ. For Reed- Solomon codes, the code minimum distance is given by: 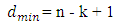



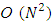 and decoding complexity of
and decoding complexity of 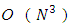 which makes them impractical for nowadays applications.The fountain code constructions we provide all have the property that encoded symbols are generated separately from one another. Moreover, we will assume that the set of receiving encoded symbols is independent of the values of the encoded symbols in that set, an assumption that is often true in practice. For a given value of k, these assumptions mean that the probability of the inability of the decoding is only dependent on how many encoded symbols are received and independent of the pattern of which encoded symbols are received.
which makes them impractical for nowadays applications.The fountain code constructions we provide all have the property that encoded symbols are generated separately from one another. Moreover, we will assume that the set of receiving encoded symbols is independent of the values of the encoded symbols in that set, an assumption that is often true in practice. For a given value of k, these assumptions mean that the probability of the inability of the decoding is only dependent on how many encoded symbols are received and independent of the pattern of which encoded symbols are received.
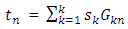
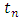 indicates to the transmitted symbols.
indicates to the transmitted symbols. 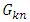 Can be generated at the transmitter side pseudo-randomly with a random seed, namely by a key, and transmitted to the receiver causing an extra overhead cost. Therefore, the symbol size is much larger than the key size, this overhead is neglectable. One other way to produce a unique
Can be generated at the transmitter side pseudo-randomly with a random seed, namely by a key, and transmitted to the receiver causing an extra overhead cost. Therefore, the symbol size is much larger than the key size, this overhead is neglectable. One other way to produce a unique  is to synchronize the receiver and the transmitter with same clock pulses and to use deterministic random number generators on both sides.
is to synchronize the receiver and the transmitter with same clock pulses and to use deterministic random number generators on both sides.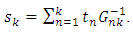
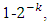 the probability that the second row is neither all zero nor same with the first row is
the probability that the second row is neither all zero nor same with the first row is 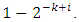 Iterating until K, we get as the overall success rate:
Iterating until K, we get as the overall success rate: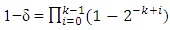
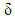 is upper bounded by
is upper bounded by 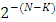 . Accordingly, each additional row increases the success probability drastically. Thus, as the message size increases, random Fountain Codes come arbitrarily close to the channel capacity. Despite a very small overhead and rate erasure independency, random Fountain Codes have a quadratic encoding complexity, k bits times the degree k/2, and cubic decoding complexity
. Accordingly, each additional row increases the success probability drastically. Thus, as the message size increases, random Fountain Codes come arbitrarily close to the channel capacity. Despite a very small overhead and rate erasure independency, random Fountain Codes have a quadratic encoding complexity, k bits times the degree k/2, and cubic decoding complexity 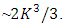 This makes them far away from most of the applications such as mobile broadcasting, where only a limited processor power can be used on the receiver side.Then, many digital Fountain coding methods have been invented such as Tornado codes, Luby transform codes and Raptor codes.
This makes them far away from most of the applications such as mobile broadcasting, where only a limited processor power can be used on the receiver side.Then, many digital Fountain coding methods have been invented such as Tornado codes, Luby transform codes and Raptor codes.
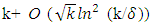 encoding symbols with probability
encoding symbols with probability  using
using 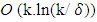 operations. However, their bit error rates cannot be decreased below some lower bound, meaning they suffer an error floor.To reduce the computational complexity, the number of edges at the encoder side should be reduced. LT codes with simple encoding and decoding algorithms can then be considered as sparse random linear Fountain Codes. Although, there are simple and fixed encoding and decoding schemes defined for LT codes the degree distributions of the edges play a crucial role in the design of good codes. Good codes are such codes, which have low encoding and decoding costs as well as a small overhead and a decoding failure. Let us start with the definitions of encoding and decoding schemes.A. LT CodingAny number of encoding symbols can be independently generated from k information symbols by the following encoding process:1) Determine the degree d of an encoding symbol. The degree is chosen at random from a given node degree distribution P (x).2) Choose d distinct information symbols uniformly at random. They will be neighbors of the encoding symbol.3) Assign the XOR of the chosen d information symbols to the encoding symbol. This process is similar to generating parity bits except that only the parity bits are transmitted.The degree distribution P (x) in Fig(6), comes from the sense that we can draw a bipartite graph, in which consists of information symbols as variable nodes and encoding symbols as factor nodes. The degree distribution determines the performance of LT codes, such as the number of encoding symbols and probability of successful decoding. The degree distribution is analyzed.
operations. However, their bit error rates cannot be decreased below some lower bound, meaning they suffer an error floor.To reduce the computational complexity, the number of edges at the encoder side should be reduced. LT codes with simple encoding and decoding algorithms can then be considered as sparse random linear Fountain Codes. Although, there are simple and fixed encoding and decoding schemes defined for LT codes the degree distributions of the edges play a crucial role in the design of good codes. Good codes are such codes, which have low encoding and decoding costs as well as a small overhead and a decoding failure. Let us start with the definitions of encoding and decoding schemes.A. LT CodingAny number of encoding symbols can be independently generated from k information symbols by the following encoding process:1) Determine the degree d of an encoding symbol. The degree is chosen at random from a given node degree distribution P (x).2) Choose d distinct information symbols uniformly at random. They will be neighbors of the encoding symbol.3) Assign the XOR of the chosen d information symbols to the encoding symbol. This process is similar to generating parity bits except that only the parity bits are transmitted.The degree distribution P (x) in Fig(6), comes from the sense that we can draw a bipartite graph, in which consists of information symbols as variable nodes and encoding symbols as factor nodes. The degree distribution determines the performance of LT codes, such as the number of encoding symbols and probability of successful decoding. The degree distribution is analyzed.
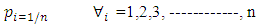

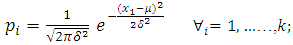
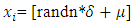 3) Sequential distribution:
3) Sequential distribution:
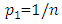
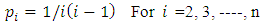
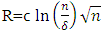 where c and
where c and 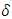 are extra parameters; c > 0 is some suitable constant.
are extra parameters; c > 0 is some suitable constant. 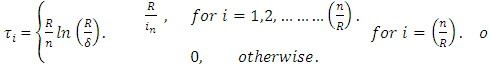



 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML