1. Introduction

The newly emerging technologies in the field of smart antennas have resulted in the development of space time coding techniques. These techniques are much more effective than conventional diversity techniques by employing information coding and signal processing simultaneously both at the transmitter and receiver [1], [2], [3], and [4]. Multiple antennas also introduce antenna diversity (also known as space diversity) into the communication system. The major problem with the receiver diversity is the cost, size and power consumption constraints. For this reason, transmit diversity scheme are very attractive.

Space-time block codes is a transmit diversity scheme with optional receive diversity to accomplish high data rate and to improve the reliability of a wireless channel. Since the pioneer work of Alamouti orthogonal space-time block coding for two transmit antennas (OSTBC) [5] has shown remarkable performance due to their low decoding complexity. According to V. Tarokh, H. Jafarkhani, and A. R. Calderbank when three or four transmit antennas were considered, the maximum symbol transmission rate of the complex OSTBC with the linear processing was 3/4 [6-8]. Due to this drawback Quasi orthogonal space-time codes relax the orthogo nality constraint of to enable rate-one transmission, at the expense of an increase in decoding complexity. For example, quasi orthogonal codes for four antennas were proposed independently by Jafarkhani [9], C. F. Mecklenbrauker and M. Rupp [10] Tirkkonen - Boariu-Hottinen [11] and Papadias-Foschini [12].

2. Existing GCOD Space Time Block Codes for N = 4 Transmit Antennas

Tarokh, Jafarkhani, and Calderbank [5] Proposed Complex orthogonal designs for four transmit antennas with code rate ½ based on above is given by

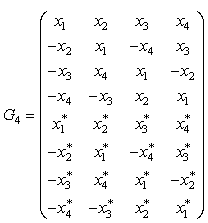An STBC is defined by p * n code matrix, where p represents the number of time intervals for transmitting k symbols, resulting in a code rate of R = k/p. At the receiver to recover symbols Maximum likelihood decoding algorithm is used.

3. New GCOD Space Time Block Codes for N = 4 Transmit Antennas

We presented GCOD Space time block codes for four transmit antennas, which can send 4 information symbols in a block of 8 channel uses and hence have rate ½ and G4 complex orthogonal design as follows:

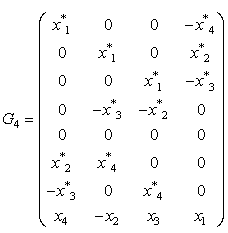The received signals during eight time slots can be expressed as

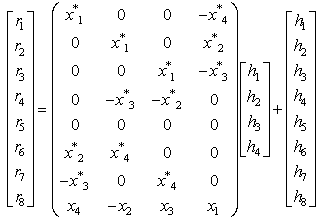At the receiver Maximum likelihood decoding is achieved in a simple way through decoupling of the signals transmitted from different antennas to recover original signals

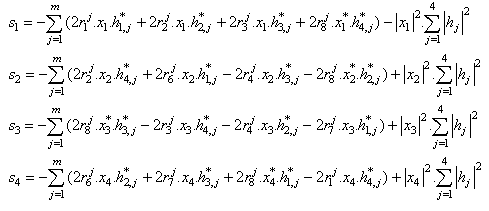We presented GCOD Space time block codes for four transmit antennas, which can send 4 information symbols in a block of 7 channel uses and hence have rate 4/7 and G4 complex orthogonal design as follows:

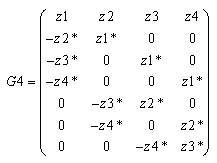The received signals during eight time slots can be expressed as

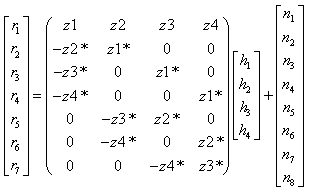At the receiver Maximum likelihood decoding is achieved in a simple way through decoupling of the signals transmitted from different antennas to recover original signals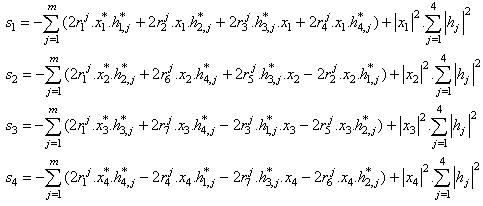

4. New GCOD Space Time Block Codes for N = 8 Transmit Antennas

The QOSTBC below matrix provides a rate R = 3/4 by transmitting six symbols in eight time slots.

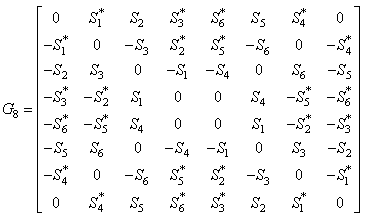The corresponding non orthogonal condition gives with G₈ as follows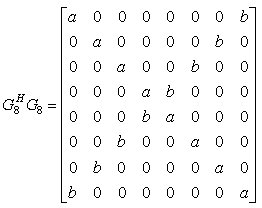

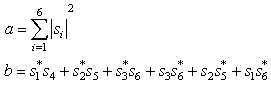Decoding analysis:

In this design the transmission matrix columns are divided into groups. While the columns within each group are not orthogonal to each other, different groups are orthogonal to each other. We call such a structure a quasi-orthogonal design. We show that using a quasi-orthogonal design, pairs of transmitted symbols can be decoded separately. We were decoding when there is one user.. Assuming perfect channel state information is available; the receiver computes the decision metric

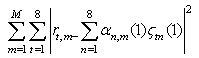Over all possible symbols to replace 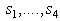with C and to decide in favour of constellation symbols that minimize the sum. Since we have only one user and for simplicity we specify one receiver antenna, and do not mention indexing of group of or receive antenna. Simple algebraic manipulation shows that ML decoding.

We proved that this metric is the sum of 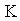components each consisting of only the variable 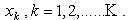Indeed, if the metric (4.4) is expanded, the cross terms involving 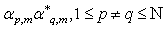are canceled out since 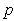th and 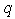th columns of 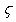are orthogonal to each other. Thus the sum has 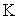components involving only the variable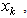 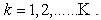It can be further proved that each component can be computed using only linear processing [3].

In this code if we define 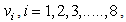as the 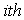column, we have

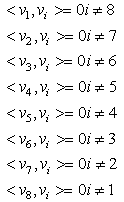(11)

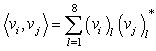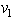Where is the inner product of vectors and Therefore, the subspace created by and 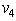is orthogonal to the subspace created by 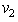and 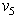. and the subspace created by 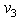and 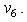Using this orthogonality, the maximum-likelihood decision metric can be calculated as the sum of the three terms 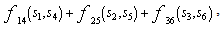where 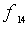is independent of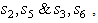 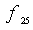is independent of 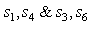and 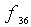is independent of 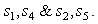In other words first the decoder finds the pair 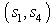that minimizes the 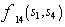among all possible 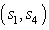pairs, next the decoder selects the pair 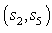which minimizes the 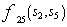and next the decoder selects the pair 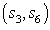which minimizes the 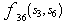This reduces the complexity of decoding without sacrificing the performance. The pairs 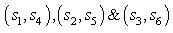can be decoded separately and the scheme is pair wise decidable.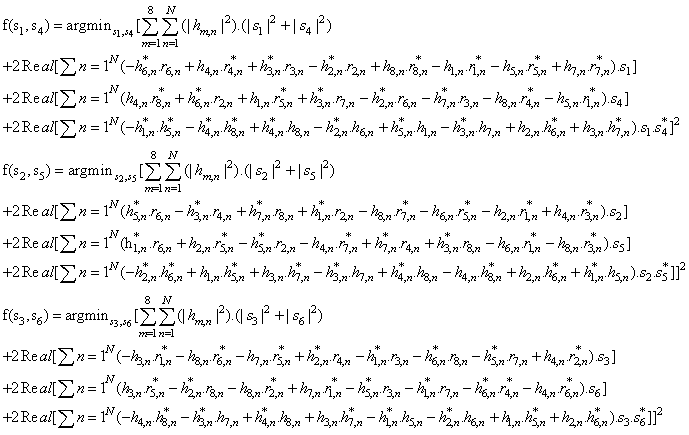

5. Results

Existing system

Proposed system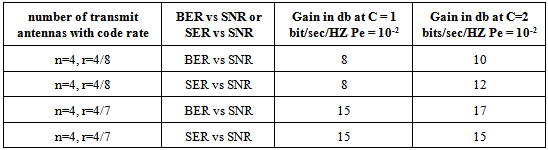

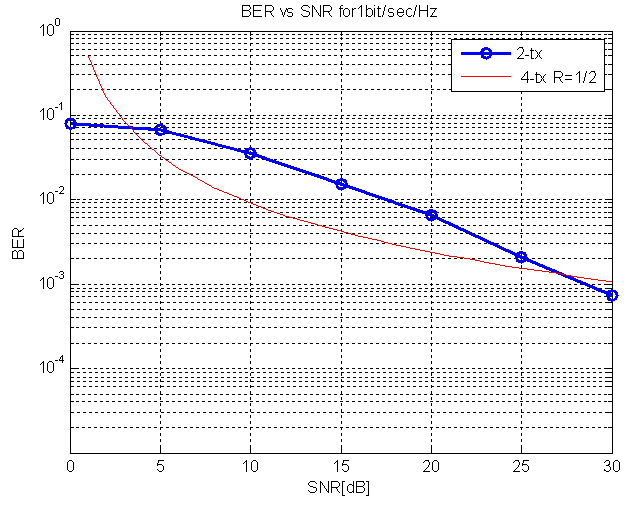
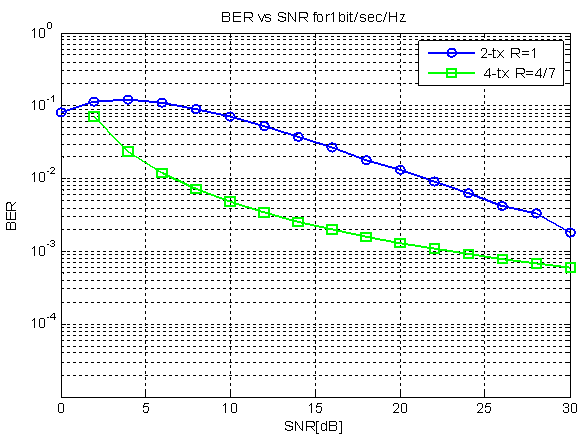Figure 1. BER of STBC for four tx.antennas with code rate 4/7 of 1bit/sec/Hz

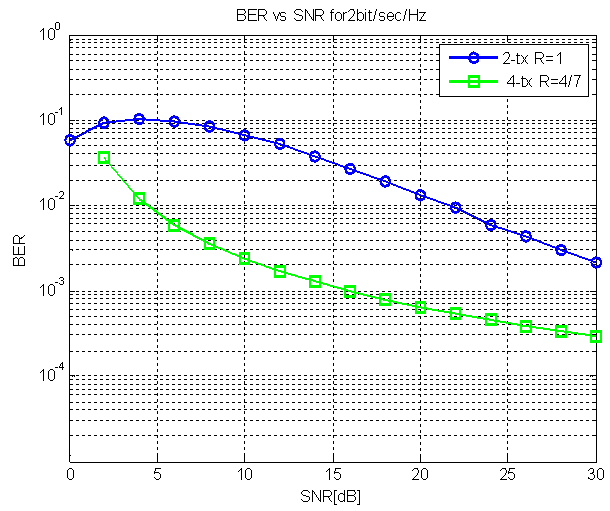Figure 2. BER of STBC for four tx.antennas with code rate 4/7 of 2bit/sec/Hz

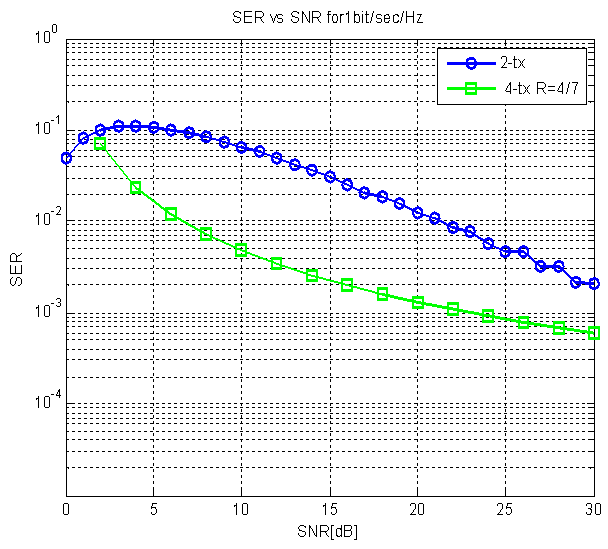Figure 3. SER of STBC for four tx.antennas with code rate 4/7 of 1bit/sec/Hz

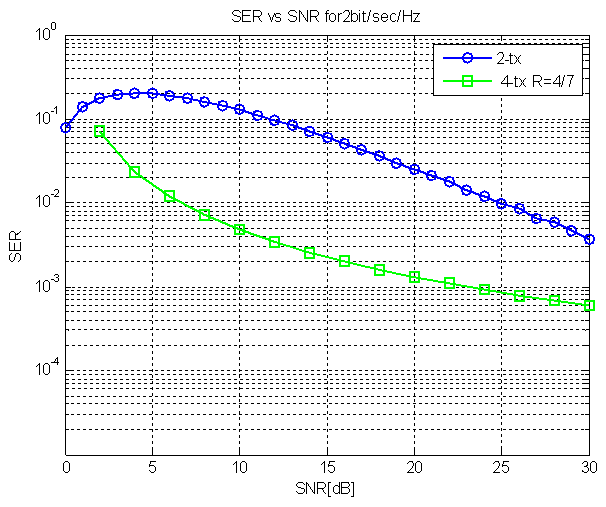Figure 4. SER of STBC for four tx.antennas with code rate 4/7 of 2bit/sec/Hz

Figure 5. BER of STBC for four tx.antennas with code rate ½ of 1 bit/sec/Hz

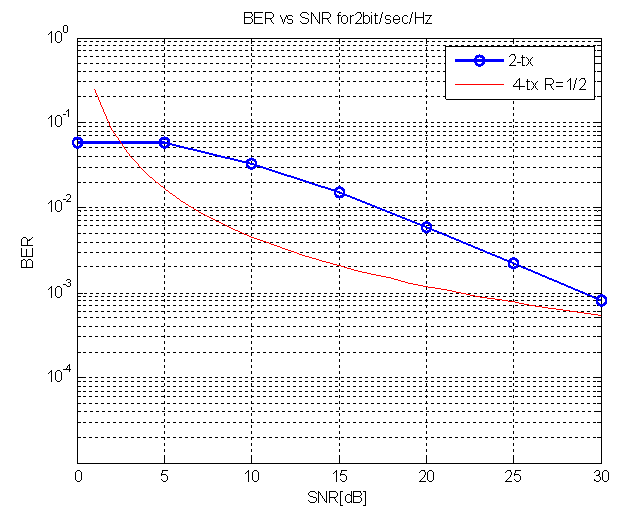Figure 6. BER of STBC for four tx.antennas with code rate ½ of 2 bit/sec/Hz

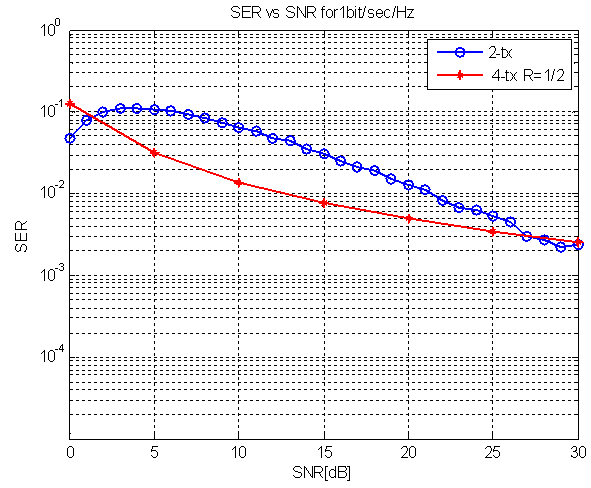Figure 7. SER of STBC for four tx.antennas with code rate ½ of 1 bit/sec/Hz

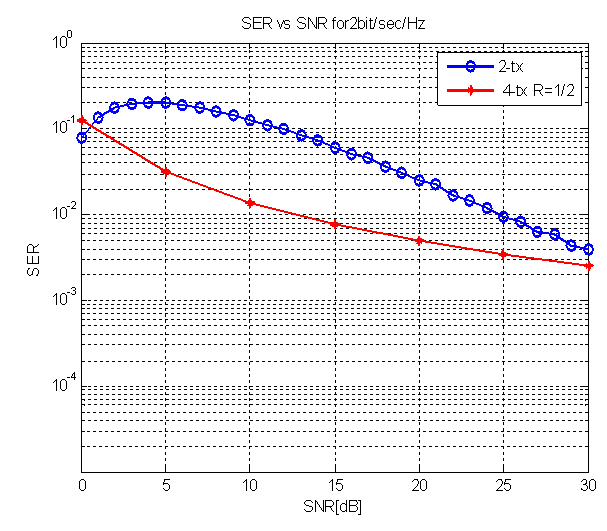Figure 8. SER of STBC for four tx.antennas with code rate ½ of 2 bit/sec/Hz

Simulation results of the performance of four transmit antenna with Alamouti two transmit antenna for Bit error probability vs signal to noise ratio at , significant gain achieved is 2.0db.New system

Simulation results of the performance of Eight transmit antenna with jafarkhani four transmit antenna for Bit error probability vs signal to noise ratio at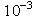, significant gain achieved is 4.0db.

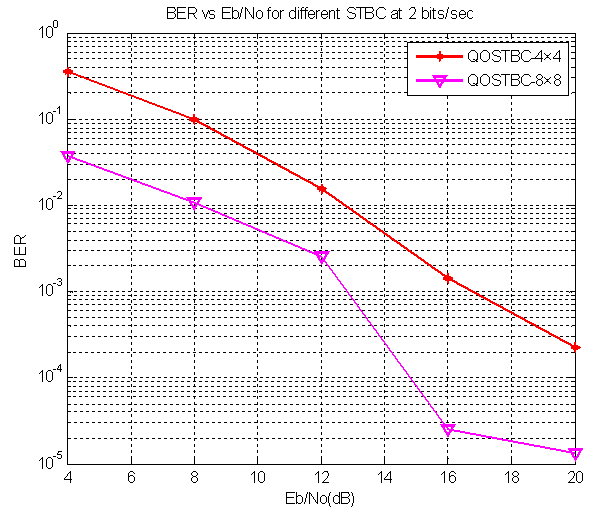Figure 9. Comparison of QOSTBC 4X4 with 8X8 QOSTBC

6. Conclusions

The performance of Space Time Block Codes for 1 bit/sec/HZ and 2 bits/sec/HZ using BPSK, QPSK Modulation Schemes for four transmit antennas with code rate of 1/2 and 4/7 is evaluated. By increasing the code rate of the system using four transmit antennas, significant gains are achieved compared to existing system. The performance of 4*4 QOSTBC with 8*8 QOSTBC for 2 bits/sec/HZ using QPSK Modulation Schemes for four and eight transmit antennas with code rate of 1 and 3/4 is evaluated. By increasing number of transmit antennas (8*8 QOSTBC) significant gains are achieved compared to existing system (4*4 QOSTBC).