Gokul Bhat , Janise McNair
Wireless and Mobile Systems Lab (WAMS), Department of Electrical Engineering, University of Florida, Gainesville, U.S.A.
Correspondence to: Gokul Bhat , Wireless and Mobile Systems Lab (WAMS), Department of Electrical Engineering, University of Florida, Gainesville, U.S.A..
| Email: |  |
Copyright © 2015 Scientific & Academic Publishing. All Rights Reserved.
Abstract
Delay and jitter are important performance metrics for streaming media as they are known to directly impact user experience. There are several sources of delay observed for streaming media in the internet such as the propagation delay, encoder delay, decoder delay and access delay to name a few. Significant amount of research has gone into minimizing different source of delay to provide a better user experience. The objective of this work is to present an analytical framework to achieve minimum access delay and jitter at the source of a streaming media characterized by variable bit-rate arrivals. Among several performance enhancing techniques for streaming high quality media, we focus on the impact of linear coding-based rate control at the transport layer as it has been established that coded transmission at the transport layer provides better overall performance for streaming media transmission. Since the development of practical network coding, many approaches have achieved receiver-based optimum delay as the decoding delay is considered to be an important element affecting network throughput. However, our work looks at the streaming system from the perspective of the source and aims to optimize the delay caused at the transmitter. Consequently, we formulate a dynamic programming problem to optimize access delay and jitter costs at the source for a streaming system based on the Markov Decision Process (MDP) model, to analyze a network-coded transport layer. Linear coding influences rate control at the transport layer and we analyze its impact on the streaming flow from an end-to-end perspective. For timely and uninterrupted streaming, achieving optimal queue service at the sender is essential and we use an approximate dynamic programming algorithm, “Value Iteration” to arrive at acceptable minimum access delay and jitter by maintaining the span norm error close to almost zero.
Keywords:
Dynamic programming, Intra-session network coding, Markov Decision Process, Span norm error, Value iteration, Video streaming
Cite this paper: Gokul Bhat , Janise McNair , An Iterative Approach to Minimize access Delay and Jitter for Streaming Media over Internet, Journal of Wireless Networking and Communications, Vol. 5 No. 1, 2015, pp. 1-8. doi: 10.5923/j.jwnc.20150501.01.
1. Introduction
VIDEO streaming traffic accounts for 66% of all consumer internet traffic and is projected to go upto about 80% by 2018 [1]. With high volume of video traffic, there is need to deliver high quality video under strict timeout deadlines. Due to the type of video and the encoding for delivering high quality media [2], it is observed that frames of varying sizes are created and passed down the network stack. This varying frame-size arrival adds to the existing rate control challenges at the transport layer to deliver video in a reliable manner. Further, streaming across wireless networks adds to the challenges in delivering high quality video owing to varying channel and network conditions. Quality of video has been evaluated using several metrics like Peak Signal-to-Noise Ratio (PSNR), Mean Square Error (MSE), goodput, delay and jitter among others [3]. The focus of the first two metrics are primarily on the impact video encoding has on the quality of generated video encoded frames and how much information is lost at the end of the encoding process. The rest of the metrics can represent different aspects of streaming media delivery depending on the layer at which they are measured. While, Peak Signal-to-Noise Ratio (PSNR), Mean Square Error (MSE) focus on the impact video encoding has on the quality of generated video encoded frames, metrics such as delay, jitter and goodput [3] if measured at the transport layer take into account the impact of network behavior on streaming delivery. Reliability is provided to streaming transmission by utilizing rate control techniques such as those provided by SCTP (Streaming Control Transmission Protocol) [4] and RTP (Real Time Transmission Protocol) [5]. In addition to several variants of TCP, especially for web-browser based video streaming [6], Forward Error Correction (FEC) techniques [7, 8] have also been employed to mitigate losses occurring in wireless networks. It has been demonstrated that network coding provides significant benefits to such streaming services in a wireless environment as it improves the network throughput and reliability of transmission [9]. In this work, we primarily focus on evaluating the access delay and jitter for streaming video from the transport layer perspective that is coupled with a linear-coding based algorithm previously described and investigated in [10, 11] because the network-centric reliability control begins at the transport layer. In related work, delay control in online network coding [12] for applications with strict time deadlines focuses on an analytical framework keeping the delay constraint as the figure of merit. However, it does not explore the impact of the arriving traffic model on the transport layer, which affects the performance, especially the delay. Similarly, in other work on rate distortion-optimized streaming [13] the receiver's buffer is tuned to receiving traffic and behavior at the user is modified than at the source. On the other hand, we investigate variable bit rate traffic arrival, sender's queue dynamics and the corresponding departure variability over the entire video transmission. 1 depicts variable bit-rate arrival traffic and the variable departure indicates the coded packet departure which may change over time to maintain low access delay and jitter. An represents the arriving traffic at time instant n and the departure Un and Un+1 are affected by the arrival as depending on the channel availability and source traffic, we have different departure patterns. The objective is to reduce the access time of the arriving traffic to be transmitted by the sender. We determine the optimum departure pattern to achieve the minimum access delay and jitter for the system model depicted in Figure 1.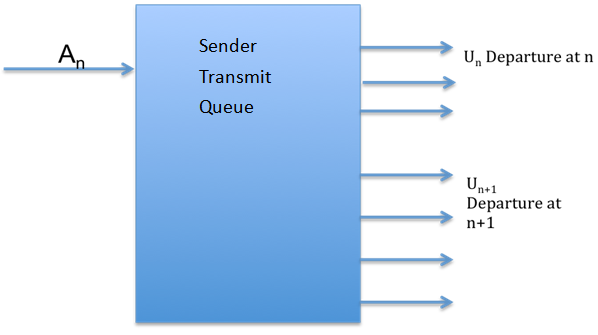 | Figure 1. Source transmit queue system model depicting the varying nature of both traffic arrival and service |
To do so we propose to use a Markov Decision Process (MDP) based model and set up a dynamic programming optimization problem where the state space includes the queue size and departure rates at the sender's transport layer. However, owing to the curse of dimensionality, the solution to the problem is obtained by using an iterative algorithm called value iteration to obtain an optimum policy that yields minimum delay and jitter for a streaming source. To the best of our knowledge, none of the previous work has looked at the sender's service rate based on the traffic arrival and coded departure which is represented by a bulk-service rate to minimize delay and jitter. Thus, the contribution of our work is to: i) model the streaming service source with a focus on arrival and bulk-departure rates using MDP; ii) formulate a dynamic programming problem to achieve minimum access delay and jitter for variable bit rate arrivals and iii) determine an optimum policy that achieves ii within acceptable error.Section 2 presents the requisite background to our work. Section 3 presents the system model and problem definition while section 4 describes the iterative algorithm used to solve the optimization problem. In section 5, we discuss the numerical results obtained and provide the conclusion in section 6.
2. Background
2.1. Why Approximate Dynamic Programming?
Based on the system model shown in Figure 1, the queue state and departure state form a Markov model as every new state can be expressed in terms of only the previous state and the corresponding input. We divide our problem of optimizing the cost into smaller sub-problems by evaluating the cost for every possible state in the state space. The state space in consideration is two-dimensional and grows quadratically which means arriving at a precise solution is impractical and there are approximate methods that can help achieve a solution as close to the optimum as possible. The value function, also known as the cost-to-go function gives the expected value of being in the present state and the cost of the optimal policy moving forward [14, 17]. At the stopping condition, the value function converges to yield the optimal policy for the desired objective.
2.2. Coded Transport Layer
A linear-coded transmission at the transport layer involves coding a pre-determined number of packets, known as the coding bucket size. These coded packets pass down the network stack and so, this form of service at the sender can be represented as a bulk-service where multiple packets are serviced by the transmit queue [10]. The bucket size for the next transmission opportunity is, then either an increment or a decrement to the current bucket size. In a coded transmission, there is always a possibility of source packets waiting to be transmitted to form the predetermined set of bucket size number of packets despite having the transmission opportunity. This wait time adds to the access delay at the source. The challenge is to determine the optimal change in the bucket size based on system model, the constraints and the objective. In this work, we determine the nature of this change in bucket size that minimizes access delay and jitter for the system shown in Figure 1.
3. System Model and Definitions
Consider the system state tuple to be {X} = {Q, U}. Let Qn represent the sender's queue state at time index n, An represent arrival process at the sender and Un represent service/packet departure at sender. Assume a discrete time system indexed by the frames present in the video traffic arriving at the sender's queue. The action space is defined by the increments/decrements on the service rate, Un, represented by {Y}. The following equations present the state dynamics of the system for the queue state and the departure state.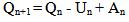 | (1) |
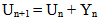 | (2) |
Yn is restricted by the Maximum Segment Size (MSS) limit on the transport layer and thus, it takes only multiples of the maximum segment size. For instance, TCP MSS is 1500 bytes and thus {Yn} = {1500, 3000, 4500, ..}. This implies that the resulting departing bucket size for instant (n+1) becomes 2, 3, 4, ... respectively. We are interested in determining an optimum change in the departure rate that leads to minimum delay and jitter. Henceforth, we use the term bucket size and the phrase “change in departure rate” interchangeably. A transmission event at instant “n” is considered successful, only when “Yn” number of packets, also called the bucket size, are successfully transmitted. Yn is also the action to be taken in this algorithm.
3.1. Cost Model
Our objective is to minimize the access delay and jitter observed at the receiver that can be calculated at the sender. We define access delay as the time taken to deliver the bucket size number of packets since their arrival at the transport layer’s transmit queue and jitter is defined as the difference between the delay in receiving two consecutive bucket size number of packets.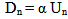 | (3) |
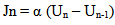 | (4) |
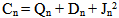 | (5) |
Using (2) and (4) in (5), we can say,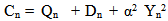 | (6) |
4. Value Iteration Algorithm
Since, we are dealing with a two dimensional state space, arriving at an exact solution for the optimal policy is not achievable practically given the large state and action space. As a result, the iterative algorithm has been implemented as shown in algorithm 1. For the algorithm to converge in reasonable amount of time, the step-size is crucial. Here the step size is decided by the limit on the packet size placed by the transport layer, which is at 1500 bytes.
4.1. Initialization
Starting with all zeros value function for the first iteration, the challenge was in mapping the randomly varying bit rate arrival of video traffic to the queue and departure states of the system. Assume that all packet units going down the network stack are constrained by a pre-determined fixed maximum size at the transport layer called maximum segment size. The queue size and departure states are thus indexed in terms of the number of maximum segment size units they represent as opposed to the actual frame index of the arriving video traffic. There are mainly two constraints applicable to the system. The departure is always at the most going to be equal to the queue size and step size of every action is limited by the maximum segment size chosen by the transport protocol.
There are mainly two constraints applicable to the system. The departure is always at the most going to be equal to the queue size and step size of every action is limited by the maximum segment size chosen by the transport protocol.
4.2. Value Iteration
The objective of the value iteration algorithm is to obtain the optimal decision space that minimizes the cost function in equation 6. To do so, we go over every possible state space tuple {Q, U} and for every possible action “k”, we calculate the cost and the corresponding value function. The value function is N*N dimensional where N corresponds to the number of {Q} states. Value function is computed as the sum of the cost of being in the current state and the average cost of arriving at a new state from the current state. This process is iteratively performed for all states and the algorithm stops when the shape of the value function does not change significantly for the next iteration. This is determined by calculating the span normal error which is maximum difference between the magnitude of the current and previous value function. The value function is convex in nature and the convexity is inherent in the algorithm. The expected cost to arrive at a new state is determined by computing the average of the value function over all the possible states which is 2*N.
5. Experiments and Results
We first present the packet size distribution of arrival traffic for the three video traces used in this experiment that highlights the aspect of the variability in the packet size distribution and hence the arrival.Figure 4 depicts the packet size distribution for 300 video frames for ''Jurassic Park'' trace [15] indicating the variability in packet sizes. The propagation delay is between 250-300 ms which is the maximum propagation delay in the internet across continental United States measured using iperf [16].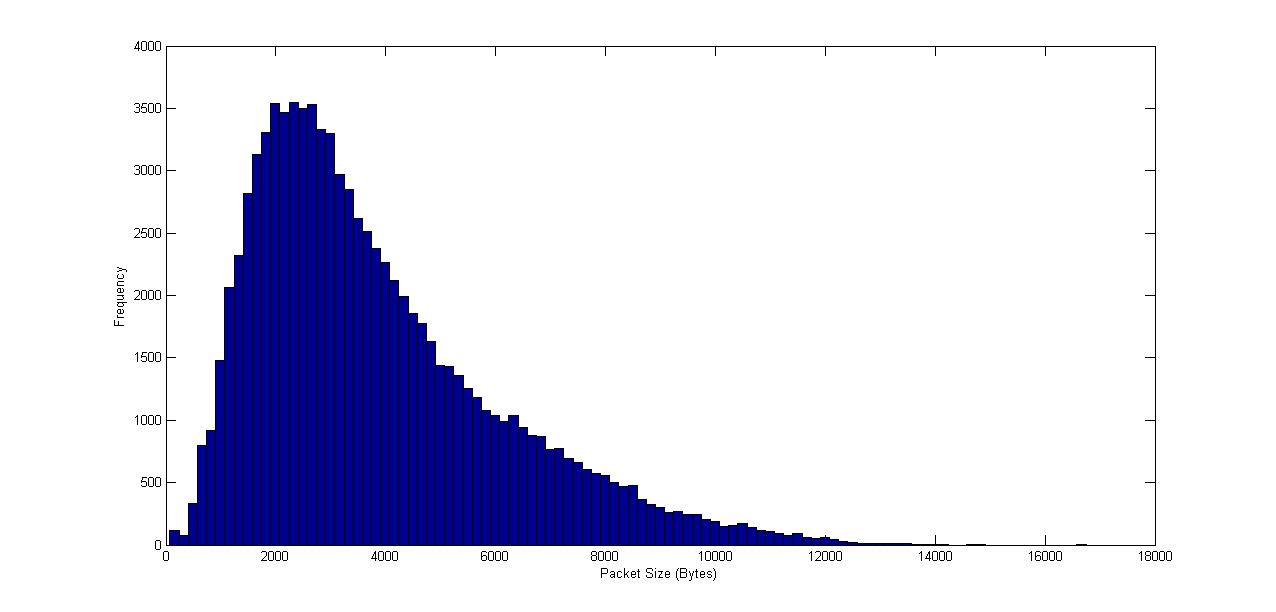 | Figure 2. Packet Size Distribution for “Jurassic Park” trace |
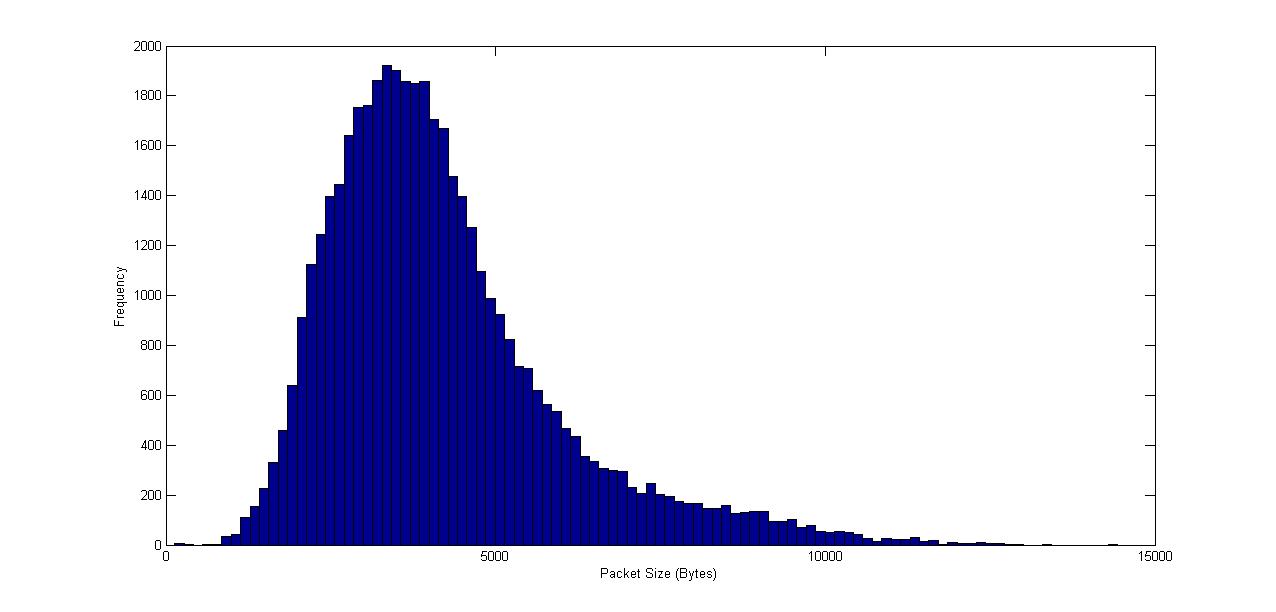 | Figure 3. Packet Size Distribution for “Silence of Lambs” trace |
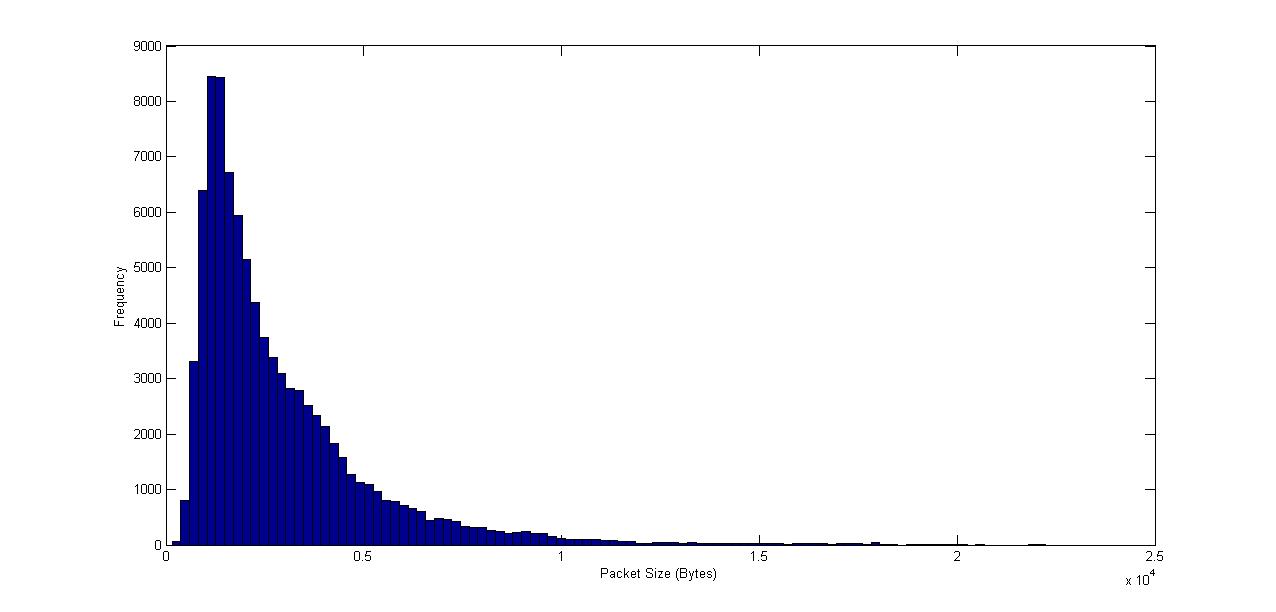 | Figure 4. Packet Size Distribution for “Formula 1” trace |
5.1. Convergence of Value Function
The stopping condition requires that the span norm error which is defined as the maximum difference between successive value functions is close to zero. This condition ensures that we arrive at a value function whose shape remains relatively same after successive iterations. In Figure 5, the behavior of the value function with respect to the departure rate is exponentially closer to the end of the video trace. The Figure 7, also indicates similar value function evolution.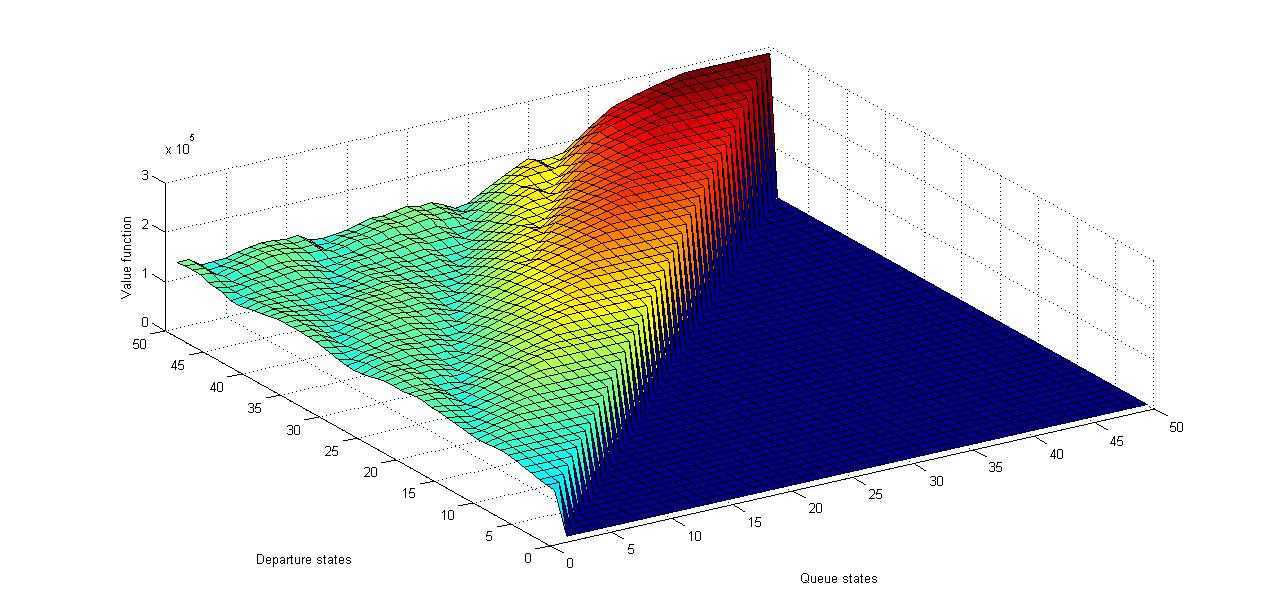 | Figure 5. Value function plot for “Formula 1” trace for all possible queue and departure states |
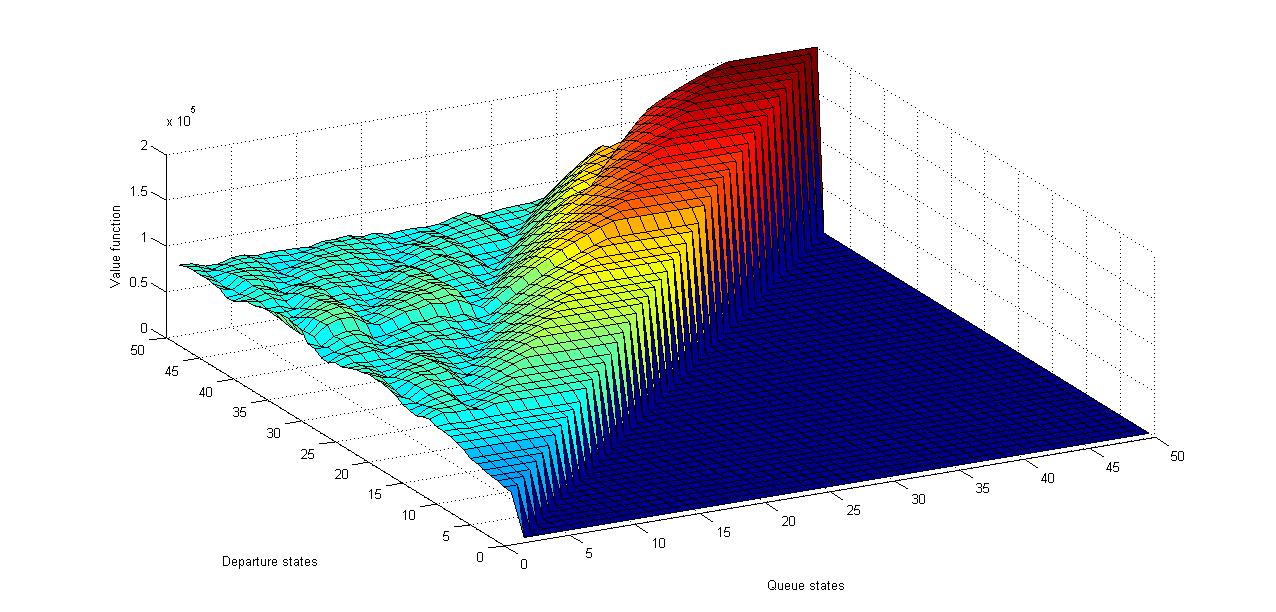 | Figure 6. Value function plot for “Silence of the lambs” trace for all possible queue and departure states |
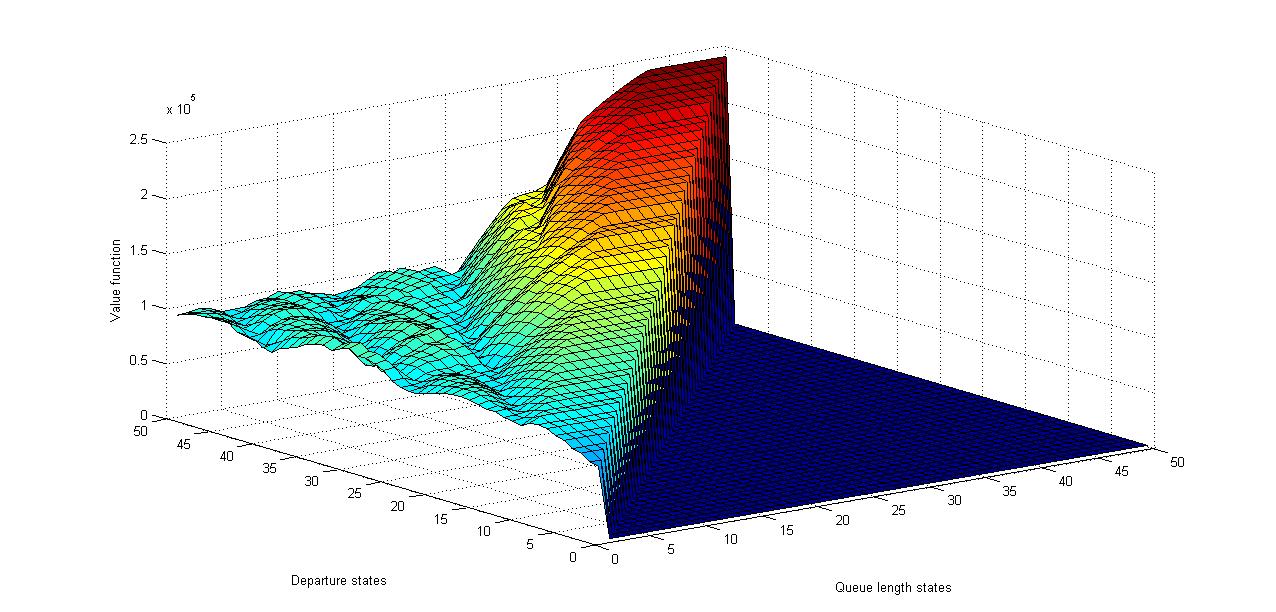 | Figure 7. Value function plot for “Formula 1” trace for all possible queue and departure states |
5.2. Action Space Evolution
For the smaller video frames, the action, which is the change in the departure rate is either one or two but for large video frames, we see that the departure rate increases to maintain the access delay and jitter at a minimum by minimizing the cost incurred.Notice in Figures 8, 9 and 10 the vertical axis indicates change in the departure rate for different frame sizes. The bulk-service departure assists in depleting the sending queue and it corroborates that a varying coding bucket size at the sender helps in optimizing streaming service at the transport layer as established in [10], [11].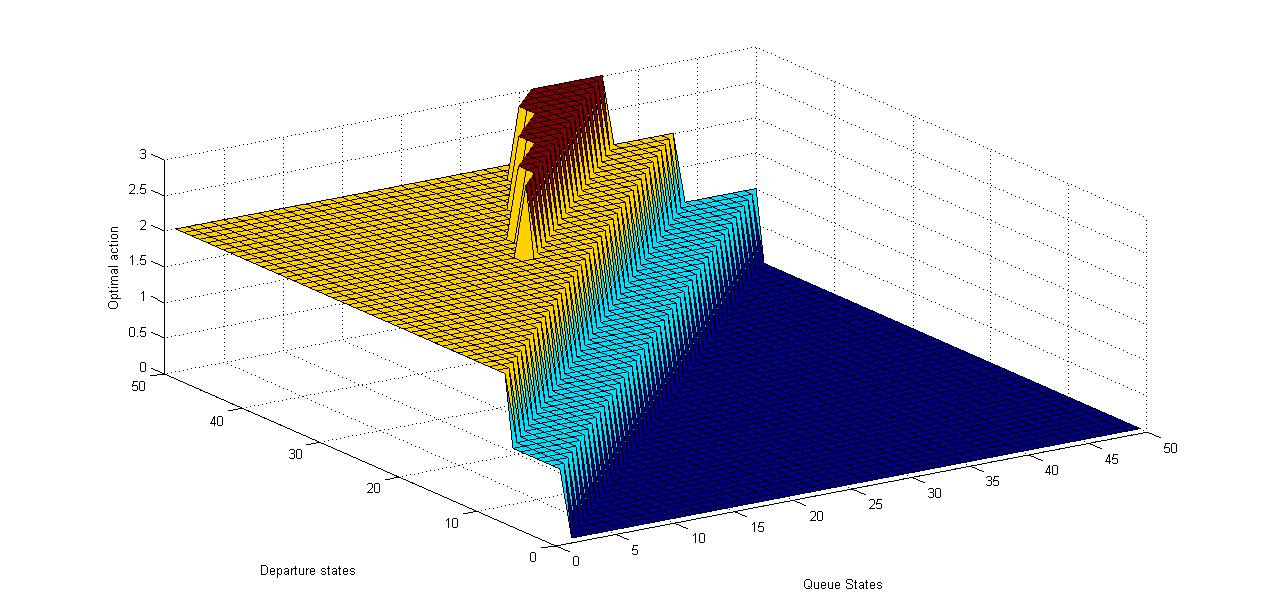 | Figure 8. Optimal action (bucket size dynamics) for “Formula 1” trace for all possible queue and departure states |
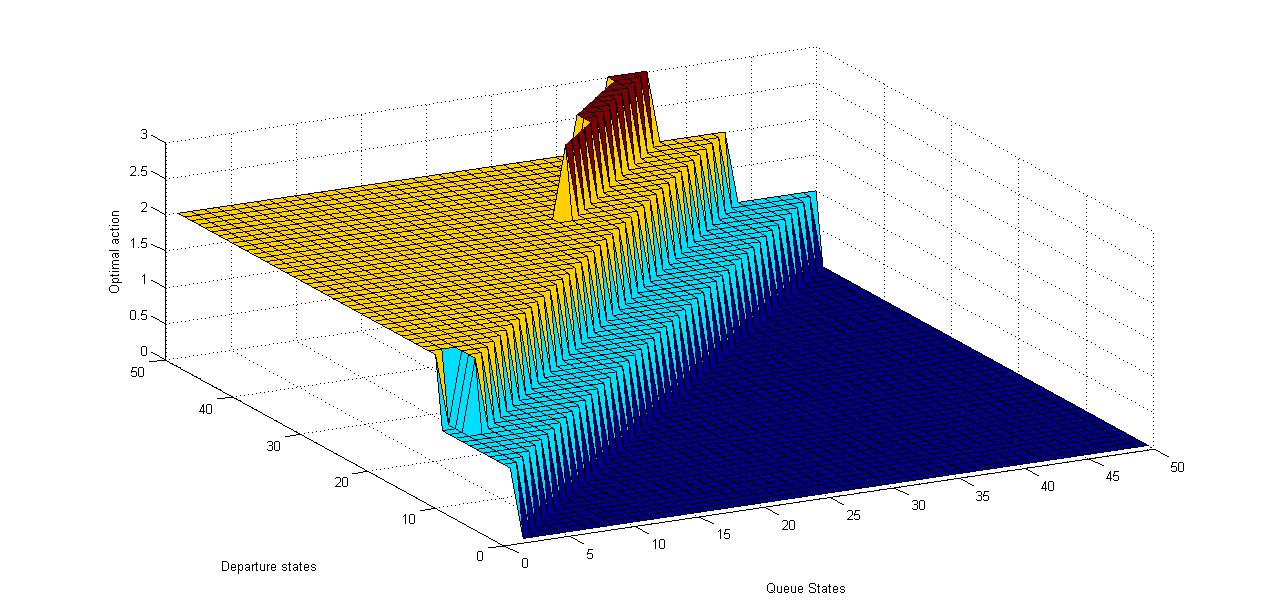 | Figure 9. Optimal action (bucket size dynamics) for “Silence of the lambs” trace for all possible queue and departure states |
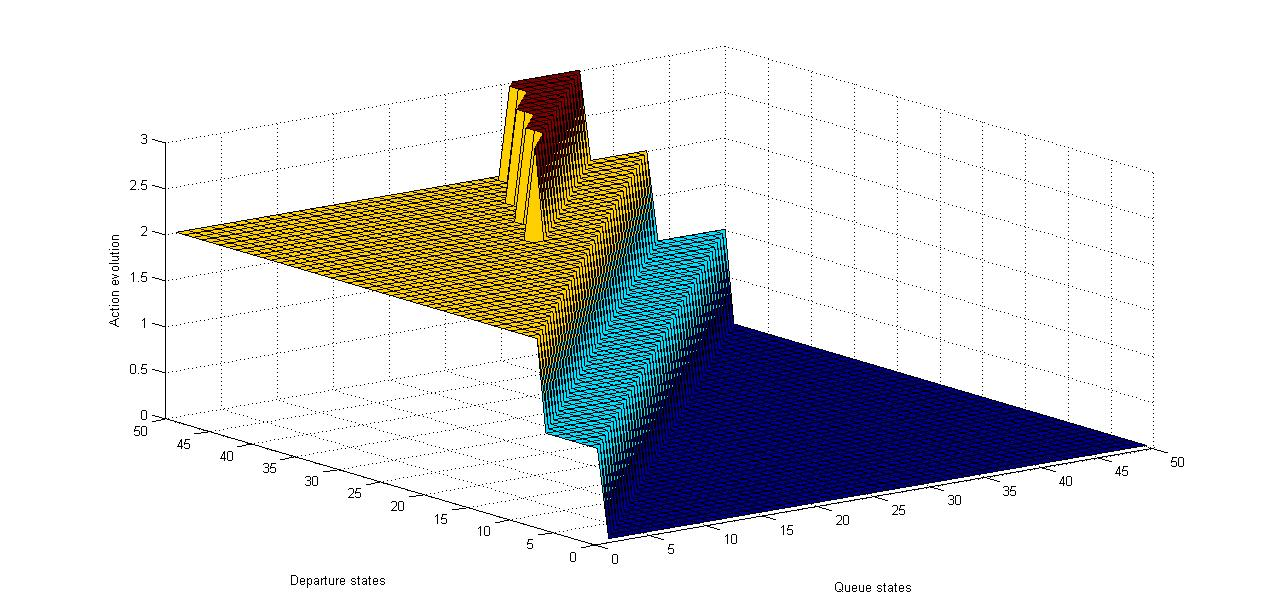 | Figure 10. Optimal action (bucket size dynamics) for “Jurassic Park” trace for all possible queue and departure states |
5.3. Impact on Transport Rate Control
We see from Figures 8, 9 and 10 that for lower departure rates and lower queue sizes, the bucket size varies between 1 and 3 while for higher departure rates, the bucket size or the increment in the departure is almost constant when the queue sizes are relatively small. But for larger queue sizes and higher departure rates, the bucket size goes up to 4 while for lower departures, the bucket size remains constant. A step-like behavior, is thus observed for corresponding queue and departure states as can be seen in the Figures.
5.4. Impact of Step Size
The step size in the algorithm is decided by the maximum segment size allowed for each transmitted segment from the transport layer perspective. It influences the number of iterations the algorithm takes to converge to an acceptable solution for the value function [17]. The step size also determines the next possible action that can be taken to go to a different queue and service state. For maximum segment size kept at the standard of 1500 bytes, the algorithm converges as early as within the first 10 iterations. Different transport protocols have different maximum sizes for transport layer data units. For instance, TCP has a maximum segment size of 1500 bytes, RTP also is in the range of 1400-1460 bytes. UDP doesn't enforce a strict limit on the maximum but is limited by the size of header field containing the message length which is 65,535 bytes.Some areas of the plots do not have any values because we have set up the simulation such that the departure can never go above the queue size and all the values corresponding to those states are thus, zero.
6. Conclusions
In this work we presented an analytical framework for a streaming service with variable bit rate arrival focusing on the coded transport layer rate control. We were particularly interested in minimizing the access delay and jitter from the sender's perspective using a generic MDP based model with constraints placed only on the queue state and the corresponding departure states. An approximate dynamic programming problem was formulated and solved using value iteration to obtain an optimal policy for the coding bucket size which was observed to be a step-function of the queue and departure states. The significance of this result lies in the fact that there is need to change the departure rate at the source to minimize one of the many sources of delay present in the internet. By minimizing access delay, we ensure that the streaming transmitter capitalizes on every transmission opportunity. An interesting extension of this work could be analyzing the importance of feedback in the state dynamics and how that impacts the cost function and thereby, the optimal policy.
ACKNOWLEDGMENTS
This work was supported by the DARPA Computer Science Study Group Program, Grant Number HR0011-09-1-0039.
Appendix
Intuition for value functionThe MDP model is a stochastic model and due to the large state space, it is impossible to get an intuition of the cost optimality in a discrete-stochastic space. In order to develop an intuition of the solution for equation (6) in the cost model, we use a fluid approximation for the states in the system. The state dynamics can, thus, be represented as,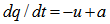 | (7) |
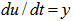 | (8) |
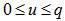 | (9) |
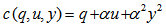 | (10) |
The Average Cost Optimality Equation (ACOE) can be written in terms of the generator polynomial, Dy,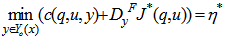 | (11) |
The right hand side term is a constant implying that the cost approaches a finite insignificant constant. The function J*(q,u) is the optimal relative value function and the generator polynomial creates the following polynomial,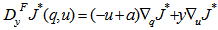 | (12) |
The gradient terms in the above expression represent the gradient of the relative value function with respect to the queue state and departure states respectively. Plugging 12 in 11 and differentiating with respect to y, gives,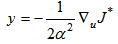 | (13) |
This represents the optimal action that satisfies equation 11. We, now guess the possible form for the relative value function. Upon expanding the equation 11, we see some power of q terms, power u terms and a few cross-terms of q and u. Thus, we can say that the value function should be of the form,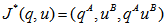 This is the kernel for the value function and clearly our intuition seems to be corroborated by figures 5, 6 and 7.
This is the kernel for the value function and clearly our intuition seems to be corroborated by figures 5, 6 and 7.
References
| [1] | S. M. Metev and V. P. Veiko, Laser Assisted Microtechnology, 2nd ed., R. M. Osgood, Jr., Ed. Berlin, Germany: Springer-Verlag, 1998. |
| [2] | J. Chakareski, S. Han, and B. Girod, “Layered coding vs. multiple descriptions for video streaming over multiple paths,” Multimedia Systems, vol. 10, no. 4, pp. 275–285, Apr. 2005. |
| [3] | R. Serral-Graci, E. Cerqueira, M. Curado, M. Yannuzzi, E. Monteiro, and X. Masip-Bruin, “An overview of quality of experience measurement challenges for video applications in ip networks,” vol. 6074, pp. 252–263, 2010. |
| [4] | L. Ong and J. Yoakum, “An introduction to stream control transmission protocol,” Internet Engineering Task Force, May 2002. |
| [5] | H. Schulzrinne and V. Jacobson, “Rtp: A transport protocol for real-time applications,” Internet Engineering Task Force, July 2003. |
| [6] | M. Ghobadi and M. Mathis, “Trickle: rate limiting YouTube video streaming,” Proceedings of the USENIX Annual Technical Conference (ATC), p. 6, 2012. |
| [7] | B. Li, Z. H. I. Wang, J. Liu, and W. Zhu, “Two Decades of Internet Video Streaming: A Retrospective View,” vol. 2, no. 3, 2013. |
| [8] | J. G. Apostolopoulos, W. tian Tan, and S. J. Wee, “Video streaming: Concepts, algorithms, and systems,” HP Laboratories, 2002, Tech. Rep., 2002. |
| [9] | S. S. Vyetrenko, “Network coding for error correction,” Dissertation, California Institute of Technology, 2011. |
| [10] | G. Bhat and J. McNair, “Modifying network coding with tcp for media streaming in ad hoc wireless networks,” Proceedings of 21st International Conference on Telecommunications, May 2014. |
| [11] | “Delivering low latency video using tcp with network coding over wireless network,” International Journal of Computer Applications, pp.1–8, February 2014. |
| [12] | J. Barros, R. A. Costa, D. Munaretto, and J. Widmer, “Effective Delay Control in Online Network Coding,” IEEE INFOCOM 2009 - The 28th Conference on Computer Communications, pp. 208–216, Apr. 2009. [Online]. Available:http://ieeexplore.ieee.org/lpdocs/epic03/wrapper.htm?arnumber=5061923. |
| [13] | P. A. Chou and Z. Miao, “Rate-distortion optimized streaming of packetized media,” no. May, pp. 1–16, 2005. |
| [14] | S. Meyn, Control Techniques for Complex Networks. Cambridge: Cambridge University Press, 2007. [Online]. Available:http://ebooks.cambridge.org/ref/id/CBO9780511804410. |
| [15] | M. Reisslein and F. H. Fitzek, “MPEG4 and H.263 video traces for network performance evaluation,” IEEE Network, no. December, pp. 40–54, Nov/Dec 2001. |
| [16] | C. hsing Hsu and U. Kremer, “Iperf: A framework for automatic construction of performance prediction models,” 1998. |
| [17] | W. B. Powell, “What you should know about approximate dynamic programming,” Naval Research Logistics, vol. 56, 2009. |

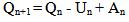
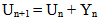
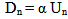
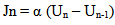
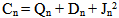
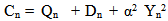
 There are mainly two constraints applicable to the system. The departure is always at the most going to be equal to the queue size and step size of every action is limited by the maximum segment size chosen by the transport protocol.
There are mainly two constraints applicable to the system. The departure is always at the most going to be equal to the queue size and step size of every action is limited by the maximum segment size chosen by the transport protocol. 








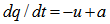
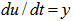
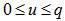
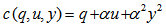
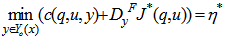
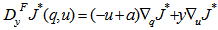
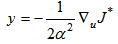
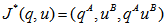 This is the kernel for the value function and clearly our intuition seems to be corroborated by figures 5, 6 and 7.
This is the kernel for the value function and clearly our intuition seems to be corroborated by figures 5, 6 and 7. Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML