1. Introduction

A Mobile Ad-hoc Network is an autonomous system of mobile devices connected through wireless ad-hoc links. Mobility management in mobile computing environments covers the methods for storing and updating the location information of mobile users who are served by the system. A hot topic in mobility management research field is mobility prediction. Mobility prediction can be defined as the prediction of a mobile user’s next movement where the mobile user is traveling between the cells of a PCS or GSM network. The predicted movement can then be used to increase the efficiency of PCSs. By using the predicted movement, the system can effectively allocate resources to the most probable-to-move cells instead of blindly allocating excessive resources in the cell-neighbourhood of a mobile user. Effective allocation of resources to mobile users would improve resource utilization and reduce the latency in accessing the resources. Broadcast program generation can also benefit from predicted mobility patterns, since the data items can be broadcast to the cell wherethe users are moving[1]. Accurate prediction of location information is also crucial in processing location-dependent queries of mobile users. When a user submits a location-dependent query, the answer to the query will depend on the current location of the user[2]. Many application areas including health care, bioscience, hotel management, and the military benefit from efficient processing of location-dependent queries. With effective prediction of location, it may also be possible to answer the queries that refer to the future positions of users.

Up until now, there has been a considerable amount of research on mobility management. Most of the research has focused on the problem of location update, which is concerned with the reporting of the up-to-date cell locations by the mobile users to the PCS network [3]. Location update should be performed whenever a mobile user moves to another cell in the network to be able to track the exact location of each mobile user. When an incoming call arrives, the network simply routes the call to the last reported location of the mobile user. Compared to the amount of work performed on location update, little has been done in the area of mobility prediction [4–6, 8-10, 12]. These works have some deficiencies, which are explained as the following:

— They seldom attempt to find mobility patterns. Instead, the patterns are assumed to be already available. These patterns are then used for mobility prediction.

— Habitually [7-9], prediction models in such cases are rooted in probability distribution of the speed and direction of the mobile user. For collecting such information, highly sophisticated and expensive tools such as GPS (Global Positioning System) are needed.

— Most of the methods studied in these works are highly sensitive to a change in a mobile user’s path. For this reason, the prediction accuracy drops in case of noisy data. These methods do not consider the difference between the randomness and the regularity in users’ paths (i.e., they do not distinguish a random movement and a regular movement of a user).

The general idea behind our method is to distinguish regularity and randomness in user movement. We examine real user mobility models for building an ad-hoc peer-to-peer network. Previous works explore randomness and regularity as two individual concepts and do not take them together for ad-hoc networks. Our objective is to examine whether a network based on the pair-wise and non-pair-wise contacts can be built or not. The novelty of our work is the conjecture that there is both regularity and randomness in user mobility which can provide complete coverage of the network. We create a user study to test our hypothesis using sequential pattern mining. We mine the access patterns of a user travelling in each node. In order to to overcome the deficiencies, we develop an effective mobility prediction algorithm as the following:

In the first phase of our two-phase algorithm, movement data of mobile user is mined for discovering regularities in inter-cell movements. These regularities are called mobility patterns. Mobility rules are then extracted from the mobility patterns in the second phase of our algorithm. The first two phases of our prediction algorithm, which are user mobility pattern mining and mobility rule generation, are accomplished offline through the system. Nevertheless, the mobility prediction is accomplished online. It means that whenever a user intends to make an inter-cell movement, a prediction request is sent to the system and the prediction is made by the system using our mobility rule based prediction algorithm [10-12]. Going over the main points again, the key contributions of our works are:

— We address the problem of group mobility movement from several parameters that directly affect Ad-hoc network partition prediction (this is the initial effort to solve this problem).

— We use sequential pattern mining to scrutinize the mobility patterns of users in mobile computing environments. Afterwards, we propose prediction accuracy model.

— We formalize our problem by introducing a principled group mobility model and propose an objective function for our problem.

— We evaluate the results obtained from simulation model. We apply group mobility pattern (GMP) algorithm with the intention of making best use of the mobility prediction algorithm.

Consequently, the effectiveness and advantage of our method are validated by a wide-ranging empirical study on a mobile user travels on a 15 by 15 hexagonal shaped network which gives a total of 225 base stations. We construct the training and test sets. The number of GAPs in training set is 9000 and the number of GAPs in test set is 1000 for supporting the experiment.

The remainder of the article is organized as follows: Section 2 presents some the background that related on the mobility models. Section 3 addresses related work. Section 4 describes the group mobility prediction based on mobility rules. Section 5 describes the experimental study and the results. Section 6 presents a conclusion and discusses some perspectives and ideas for future work.

2. Background

In this section, we described the definition terms that related on the mobility models. We classified into three categories as followings:

2.1. Random Waypoint Mobility Model

The Random Waypoint Mobility Model [13-14] is an extension of the Random Walk model. It introduces a pause after the node has reached its destination point. The pause time is uniformly distributed between a minimum and a maximum value. After the pause, the node starts moving towards the next randomly chosen destination point and the process is repeated again. The distribution of the nodes in the simulation area and the distribution of the node speeds vary over the simulation time. Even thought the speed of a node is chosen from a uniform distribution, the distribution of the node speed sampled after a long enough time will differ from the uniform distribution where the speed for the next trip is chosen from. A lower speed is more likely to be.

2.2. Reference Point Group Mobility Model

Reference Point Group Mobility Model (RPGM)[13-15] model is one of the typical group mobility models, and it has a logical center node as team leader that determined the group’s movement behavior. The movement of group leader at time, t can be represented by motion vector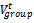,[14] provides the general motion trend of the whole group. The motion vector 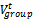can be randomly chosen or carefully designed based on certain predefined paths. The movement of group members is significantly affected by the movement of its group leader. For each node, mobility is assigned with a reference point that follows the group movement. Upon this predefined reference point, each mobile node could be randomly placed in the neighbourhood. The formally, motion vector of group member, I, at time t, 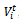, can be described as:

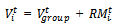(1)

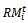From equation (1) illustrated[13], the motion vector  is a random vector deviated by group member i from its own reference point. The vector 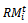 is an independent identically distributed random process whose length is uniformly distributed in the interval[0, 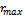] (where 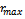is maximum allowed distance deviation) and whose direction is uniformly distributed in the interval[0, 2].

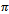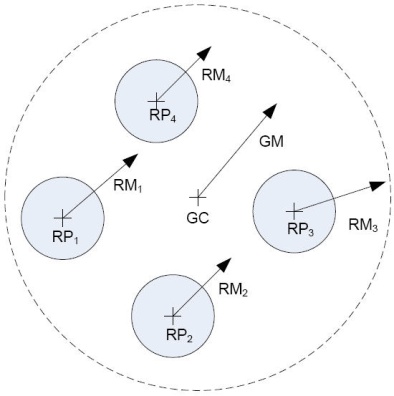Figure 1. Reference Point Group Mobility Model[3, 6]

From Figure 1 illustrates, each node has a reference point RP(t) within a certain range from the group center which is moved together with the movement of the group center. The Defense Advanced Research Projects Agency (DARPA) has classified the movement behavior of nodes for military operations and natural disaster into three categories based on the RPGM model[14-16]:

— In-Place Mobility Model: the entire field is divided into several adjacent regions. Each region is exclusively occupied by a single group. One such example is battlefield communication.

— Overlay Mobility Model: different groups with different tasks travel on the same field in an overlapping manner. Disaster relief is a good example.

— Convention Mobility Model: this scenario is to emulate the mobility behaviour in the conference. The area is also divided into several regions while some groups are allowed to travel between regions.

However, the RPGM model has two disadvantages [12, 15]: First, it has to know the complete information for the whole mobility groups, including their member nodes and movements. In natural ad-hoc network environments including tactical networks, however, such the assumption of the knowledge on global information for mobility groups can’t be achieve. Second, each mobile node's location is represented by its physical coordinates. Given only the instantaneous physical locations of the nodes, however, it is difficult to discern the nodes’ group movement patterns and the trend in the network topology changes. With the disadvantages of the RPGM model, it is difficult for the model to be applied to realistic environments.

2.3. The Reference Velocity Group Mobility Model

The Reference Velocity Group Mobility Model (RVGM)[16, 17] extended the RPGM model by proposing a velocity representation of the mobility group and the mobile nodes. The node movement is expressed by a velocity vector v = (v_x,v_y)^T; where v_x and v_y denote the velocity components in the x and y directions, respectively. In RVGM model, the velocity vector of i-th node in j-th group is obtained as following:

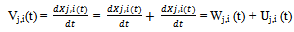(2)

From equation (2) illustrated[16], In particular, the Where W_j,i (t) and U_j,i (t) are the group velocity and the local velocity deviation vectors of the node, respectively. RVGM model based on velocity vectors or mobility angles overcomes the disadvantages of the RPGM model based on not physical coordinates. It can adapt the changes of network topology easily, also. However, it does not consider the effect by terrain of surroundings. That is, since there may appear several obstacles by terrains in battle fields, predicted mobility paths by the model may be along the obstacles which tactical nodes can’t pass through.

3. Related Work

In this section, we will first present other works related to the sequential pattern mining problem. Second, we present the research for predicting the mobile users’ group movement behaviour. Third, we present an adaptive algorithm for location management.

The sequential pattern mining problem was discussed in[7, 13]. For our domain, the mobile users are assumed to be moving between the cells of a PCS network. The algorithms proposed in[8] cannot be applied directly to our domain for mining mobility patterns, because these algorithms do not take into account the network topology while generating the candidate patterns. This weakness of the proposed algorithms gives rise to generation of candidate patterns, which cannot exist as mobility patterns on the corresponding network, since only the sequence of neighbouring cells of the network can be considered as a mobility pattern. Therefore, the number of candidates generated can be extremely high, and this factor can dramatically reduce the performance of the mining algorithm. In [1, 14], sequential pattern mining is applied to the domain of predictive Web prefetching. Web prefetching can be defined as deriving users’ future requests for Web documents based on their previous requests. For effectively predicting the users’ future requests, user access patterns are mined from the Web logs of users’ previous requests and then these patterns are used for prefetching. The method presented in[1, 7, and 13] extends existing algorithms for mining sequential patterns in order to take the graph structure of the corresponding Web site into account during support counting, candidate generation and pruning. As we describe in Section III, in the first phase of our mobility prediction algorithm, we generalize the method presented in[1, 13] to be able to mine mobility patterns of users in mobile computing environments. In the latter stages of our algorithm, mobility rules are extracted from the mobility patterns, and by using these rules, user movements are predicted. There has been a considerable amount of research in mobility prediction, as well. The work presented in[5] is among the pioneering research for predicting the mobile users’ movement behaviour. In that work, user’s moving behaviour is modelled as repetitions of some elementary movement patterns which are indeed circular and straight line patterns. In order to estimate the future location of a user, a mobile motion prediction (MMP) algorithm is proposed. However, the MMP algorithm is highly sensitive to random movements of the user. It is reported in [5] that as the random movements of the user increase the performance of MMP decreases linearly. The work in [6] proposes a two level scheme, which combines a local with a global prediction model. The top level is the Group mobility model (GMM), whose resolution is determined in terms of the cells crossed by a mobile user during the lifetime of the connection. The bottom level is the local mobility model (LMM), whose resolution is determined in terms of a 3-tuple sample space (speed, direction, position) that varies with time. LMM is used to model the intra-cell movements of the mobile users. On the other hand, GMM is used to predict the inter-cell movement trajectory of a user by matching the user’s actual path to one of the existing ‘‘mobility patterns’’. For this purpose pattern matching techniques are used. Premchaiswadi W. et. al.[10], enhance both the link layer and network layer handovers using location’s information driven from the mobile phone’s cell tower for tracking users. However, the weakness of the work is revealed at this point because there is no method presented in[4] to discover these mobility patterns, Gauss–Markov[3] model is introduced, where a mobile user’s current velocity and location is correlated in time to a various degree. Based on the Gauss–Markov model, a mobile user’s future location is predicted by the network based on the information gathered from the user’s last report of location and velocity. In [13], Aljadhai and Znati use a first-order autoregressive filter in order to determine the direction of movement of a user. It is claimed in that work that the proposed method guarantees that the predicted mobile direction is not affected by small deviations in the mobile user’s direction. In the work, Romsaiyud W. and Premchaiswadi W.[12] for location prediction cell-to-cell transition probabilities of a mobile user is calculated by the help of the previous inter-cell movements of the user, and then recorded to a matrix. Based on this, resource allocation is done at the k most probable cells that are in the neighbourhood of the current cell. Here k is a user-defined parameter. This method is called Mobility Prediction based on Transition Matrix (TM). An adaptive algorithm for location management is proposed in[16]. By building and maintaining a dictionary of individual user’s path updates, the proposed on-line algorithm can learn mobile users’ mobility patterns.

4. Group Mobility Prediction Based on Mobility Rules

In this section, we presented two algorithms: group mobility pattern (GMP) mining for generating of group mobility rules using the mined GMPs, and proposed the mobility prediction.

4.1. Group Mobility Patterns

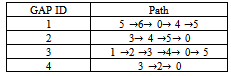
We define a group mobility pattern (GMP) as a sequence of neighbouring cells in the coverage region network [12]. The consecutive cells of a GMP should be neighbours because the users cannot travel between non neighbour cells. Indeed, GMPs correspond to the expected regularities of the group actual paths. In order to mine the GMPs from group actual paths (GAPs), sequential pattern mining [12, 14] can be used. Sequential pattern mining has been previously used and examined in various research domains. One such work has been performed in the domain of web log mining [14, 15, 18- 19]. In that work, sequential pattern mining is used to mine the access patterns of a user while visiting the pages of web sites. This method assumes the web pages to be the nodes and the links between these pages to be the edges of an unweighted directed graph, G. Then, sequential pattern mining is applied to web logs by considering G.

We design a new method that is convenient for our domain, by generalizing the method of[12, 14] and applying it for GMP mining. This new method employs

— A different definition of the graph G, and

— A new method for support counting, which generalizes the method presented in[12, 14-16].

From the group mobility pattern for traverse in the graph, assume that we have two GAPs, A = (a₁, a₂, …., a_n) and B=(b₁, b₂, …., b_m). B is a subsequence of A, if there exist integers 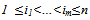such that b_k = a_ik, for all k, where 1.

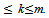In other words, B is a subsequence of A, if all cells in B also exist in A while keeping their order in B (but they do not need to be consecutive in A). Let us give an example by using the coverage region given in Figure. 2: assume A = (c₃, c₄, c₀, c₁, c₆, c₅), then B = (c₄, c₅) will be a length-2 subsequence of A. In other words, the GAP B is contained by the GAP A.

Figure 2. An example coverage region (a) the corresponding graph G (b)[11], User mobility traversal (c) and XML trace file that collects data from the starting point to the destination point (d)

Pseudocode I. GMPMining

Input: All the GAPs in the database, D

Minimum value for support, supp_min

Coverage Region Graph, G

Output: Group Mobility Patterns (GMPs), L

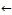1: C₁ the patterns which have a length of one

2: k=1

3: L

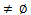4: while C_k

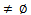5: foreach GAP a 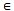D

6: S = {s | s 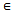C_k and s is a subsequence of a}

7: foreach s 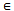S

8: s.count = s.count+s.supp_Inc

9: L_k ={ s|s 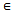C_k, s.count 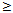supp_min}

10: L = L 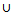L_k

11: C_k+1 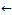CandidateGeneration (L_k, G), 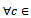C_k+1

12: c.count = 0

13: k= k+1

14: return L

From Pseudocode I, we illustrate this method of support counting treats a highly corrupted candidate pattern and a slightly corrupted (or even not corrupted at all) candidate pattern in the same way and assigns the support value of 1 to both patterns. Since this method is unfair for the context of mobile motion prediction, unlike the work in[11, 13- 14], our support counting method considers the degree of corruption, i.e., we differentiate the support given to a slightly corrupted pattern and to a highly corrupted pattern. In our method, we calculate the support assigned to a candidate pattern B by a GAP A (i.e., suppInc) by using the following formula:

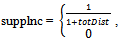(3)

if pattern B is contained by GAP A

We can define the totDist value by means of the notion of string alignment. Given two strings, where a string is a sequence of characters, Gusfield[20, 25] demonstrates methods for determining the similarity between these two strings by finding the optimal alignment between them. For instance, assume that the two strings are ‘‘acbcdb’’ and ‘‘cadbd’’. Here is one possible alignment of these two strings, where the special character ‘‘-’’ represents the insertion of a space.

4.2. Mobility Prediction Algorithm

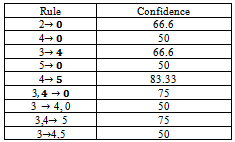
The pseudo-code for the mobility prediction phase of our algorithm is presented in a Preudocode II. In this phase, the next movement of the mobile group users’ are predicted. The prediction procedure can be summarized as follows: Assume that a mobile user has followed a path P = (c₁, c₂, . . ., c_i-1 ) up to now. The algorithm finds out the rules whose head parts are contained in path P, and also the last cell in their head is c_i-1. We call these rules the matching rules. We store the first cell of the tail of each matching rule along with a value which is calculated by summing up the confidence and the support values of the rule in an array of such tuples. The support of a rule is the support of the GMP from which the current rule is generated. The tuples of this array are then sorted in descending order with respect to their support plus confidence values. While sorting the matching rules, both the support and confidence values of a rule should be taken into consideration to select the most confident and frequent rules.

Pseudocode II. GroupMobilityPrediction Model

Input: Current trajectory of the user, P= (c₁, c₂,…,c_i-1)

Set of mobility rules, R

Maximum predictions made each time m

Output: Set of predicted cells, GCells

1: GCells =

2: k=1

3: foreach rule r: (a₁, a₂,..,a_j) 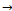(a_j+1,…,a_k) 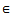R

4: if (a₁,a₂,..,a_j) is contained by P=(c₁,c₂,..,c_i-1) and a_j = c_i-1

5: MatchingRules MacthingRules 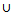r

6: TupleArray[k] = (a_j+1, r.confidence+r.support)

7: k = k+1

8: TupleArray sort(TupleArray)

9: index = 0

10: while (index < m && index < TupleArray.length)

11: GCells GCells TupleArray[index]

12: index = index+1

13: return GCells

From Pseudocode II, we illustrate this method of parameter, m; which is the maximum number of predictions that can be made each time the user moves. For prediction, we select the first m tuples from the sorted tuples array[12, 21, 26-27]. Then the cells of these tuples are our predictions for the next movement of the mobile user group. It means that we use the first m matching rules that have the highest confidence plus support value for predicting the group user’s next movement.

5. Experimental Results

For simulation, we have adapted the simulation model which is presented in our earlier work[23, 29-30]. In this model, it is assumed that a mobile user travels on a 15 by 15 hexagonal shaped network which gives a total of 225 base stations. In order to generate the group actual paths (GAPs), first a number of group mobility patterns (GMPs) is generated. The length of a GMP is determined by a uniform distribution with a mean length l. Each GMP is taken as a random walk over the hexagonal network[26]. There are two types of GAPs generated. The first type consists of GAPs that follow a GMP and the second type consists of outliers (i.e., those which do not follow a pattern). The ratio of the number of outliers to the number of GAPs that follow a GMP is denoted by 0. For each new GAP we decide whether it is going to be an outlier or not, according to the value 0. If it is an outlier, then it is formed as a random walk over the hexagonal network. Otherwise, a GMP is selected randomly that will correspond to the generated GAP. We also use a corruption mechanism to distinguish the GAP from its corresponding GMP. We insert random cells between the consecutive cells of the GMP. In order to accomplish this, we define a corruption ratio c, which denotes the ratio of the number of such random cells to the number of cells in the corresponding GMP. The total number of generated GAPs is 10,000 and from these, we construct the training and test sets. The number of GAPs in training set is 9000 and the number of GAPs in test set is 1000. GMPs are mined from the GAPs in the training set and then the mobility rules that will be used in prediction are generated by using these GMPs. The GAPs in the test set are used for evaluating the prediction accuracy of our algorithm. There are three possible outcomes for the location prediction, when compared to the actual location:

— The predictor correctly identified the location of the next move.

— The predictor incorrectly identified the location of the next move.

— The predictor returned ‘‘no prediction’’.

Table 1. The variable and value in our experiment Definition Default Values Maximum number of predictions made each time (m) 2 Average length of GAPs (l) 5 Corruption factor (c) 0.4 Minimum support percentage (Suppmin) 0.1% Minimum confidence percentage(confmin) 80%

We compared our GMP-based mobility prediction method with two different prediction methods. The first method is the Movement Circle (MC) and Movement Track (MT) models[22], which efficiently extended the Markov model in mobile applications for modeling the movement of mobile users. The MC algorithm is based on the closed circuit-like (MC) model of user movement behaviors and is used for predicting long-term regular movement. Such closed circuits, representing a return to a previous state, are topologically a circle. The MT algorithm based on the MT model is used for predicting the routine ones. Three classes of matching schemes are used for correlation analysis of MCs or MTs. The second prediction method is the TM Prediction, which is presented in[12, 25, 28]. MC/MT Prediction method disregards the information available from movement history. To predict the next inter-cell movement of a user user’s group, this method assigns equal transition probabilities to the neighbouring cells of the user’s group currently residence cell. It means that prediction is performed by randomly selecting m neighbouring cells of the current cell. It is a very primitive algorithm and we used it as a base algorithm to observe the system performance when no location prediction is made based on a prior knowledge of user movements.

The first experiment is conducted for choosing the m (the maximum number of predictions made each time) value which is appropriate for all the methods. The next two experiments are conducted for tuning the parameters of our method, which are: supp_min (the minimum support threshold used in GMP mining algorithm) and conf_min (the minimum confidence threshold used in mobility rule generation algorithm). In these experiments, we search for the best values for each parameter that make both recall and precision good. The last two experiments are to measure the performance of our method as compared to the performance of other methods. We also measured the average time required to make a single prediction with each algorithm. For our algorithm, computation of the predicted cells requires a time in the range of 10–50ms for all cases in the experiments. This is the time needed for the online computation of the predicted cells when a prediction request arrives at the system. Considering the fact that a user who reaches a cell would most probably stay in it for a period of time that is much larger than 50 ms, the prediction time is a negligible overhead. The mobility rule mining phase of our algorithm is executed offline just for once. Thus, the time needed for the offline phase can be neglected. The other two algorithms make their predictions in shorter time, since they involve less computation in determining locations as shown on Figure3.

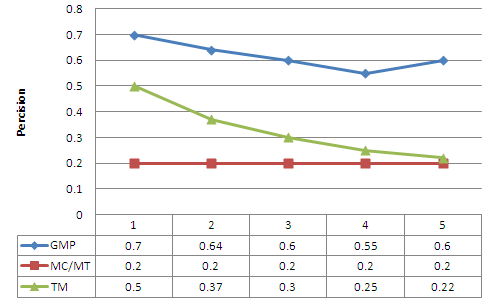Figure 3. Precision as a function of the maximum number of prediction made each time

From Figure 3, we illustrate the first experiment; we examine the performance impact of parameter m, maximum number of predictions made at each move of user. In the result, the precision obtained by our method and the precision obtained by TM decrease as m increases. The decrease in precision obtained by TM is more dramatic when compared to that obtained by our method. The decrease in both precision values is due to the fact that as the number of predictions made at each movement of the user increases, the probability of having some incorrect predictions gets higher. Therefore, the number of correct predictions made by our method and TM does not increase in the same rate with the number of predictions. On the other hand, the precision obtained by MC/MT Prediction method remains almost constant as m increases, ignoring some statistical variations. It is around 0.2 for all m values. As m increases, the total number of predictions and the number of correct predictions for this method increase at the same rate. This explains why the precision of the MC/MT method is fixed at 0.2. This value is very low when compared to the value obtained by our method.

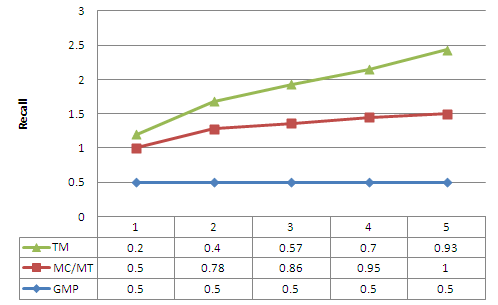Figure 4. Recall as a function of the maximum number of prediction made each time

From figure 4, we illustrate the recall values for all methods increase with increasing m as shown in Fig. 4. This observation can be explained by the fact that as the number of predictions made at each move of the mobile user increases, the probability of predicting the correct cell increases. The increase in recall values with TM and MC/MT methods are more significant when compared to the increase with our method. For our method, beginning from m = 3, recall values do not increase significantly and become almost fixed at around 0.5. This is because the number of matching rules is the same for all m values. Beginning from some m value, the number of correct predictions does not increase because the m value exceeds the number of matching rules. Therefore, the number of correct predictions becomes stable making the recall value stable. For TM and MC/MT methods, recall values increase steadily, finally reaching to 1.

From Figure 5, we illustrate the effect of increasing minimum support (supp_min) value on the recall and precision values obtained by our method. It is shown in Figure. 5 that as the supp_min increase, the precision and recall values decrease. This is due to the fact that the increase in the supp_min value leads to a decrease in the number of mined mobility rules. Therefore, the number of correct predictions is reduced. This causes the recall and the precision values to decrease. Since both recall and precision values decrease for increasing supp_min, it would be most appropriate to choose supp_min = 0.1 which is the smallest value used in the experiments. We have observed that recall and precision values do not increase considerably (it can even be said that the values do not increase at all) for the supp_min values smaller than 0.1.

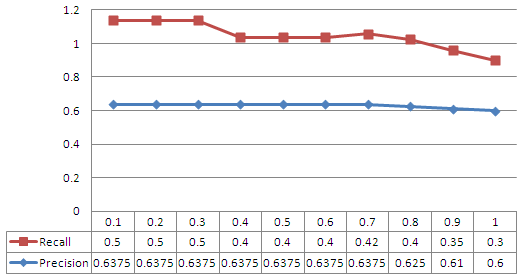Figure 5. Precision and Recall as a function of the minimum support for GMP prediction model

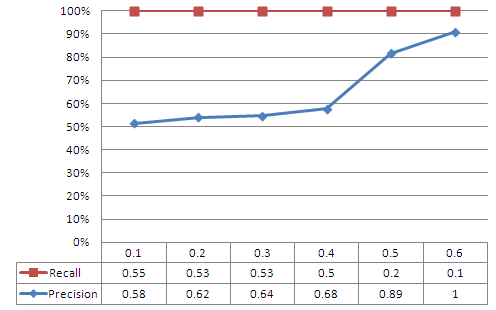Figure 6. Precision and Recall as a function of the minimum confidence for GMP prediction model

From figure 6, we examine the effect of increasing minimum confidence (conf_min) values on the recall and precision of our method. Figure 6 indicates the impact of minimum confidence on the precision. As one can realize, the precision increases as conf_min increases. Even, the precision reaches to very high values such as 0.99 at conf_min = 100. Because, at high conf_min values, only the rules that have high confidence values are used for prediction. As a result, the number of rules used for prediction is reduced and their quality gets higher with the increasing conf_min. This leads to a higher decrease rate in the number of predictions when compared to the decrease rate in the number of correct predictions. Therefore, the precision value improves as conf_min increases.

From figure 7 and 8, we examine the effect However, the precision obtained by our method is better than the precision obtained by its closest competitor, which is TM. This is true for all corruption values. Although the MC/MT Prediction method demonstrates a stable precision value, it presents the worst performance for precision. This indicates the ineffectiveness of the MC/MT Prediction method. The recall value also drops for both our method and TM with the increasing corruption factor. For our method, we can explain this by the decreasing number of mined rules. As the corruption in the data increases, the GAPs will provide less support to large patterns. This leads to a decrease in the number of GMPs mined by our algorithm. As a result, the number of mobility rules which are determined by our algorithm decreases. There is another reason for the performance reduction of our method. As a result of the corruption, our prediction algorithm will match less or even will not match any mobility rules to the current trajectory of a mobile user. Therefore, no prediction can be accomplished in many cases when the corruption gets very high.

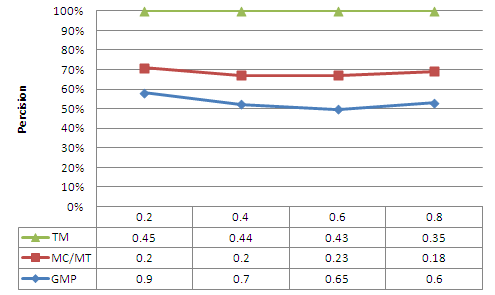Figure 7. Precision as a function of the corruption factor

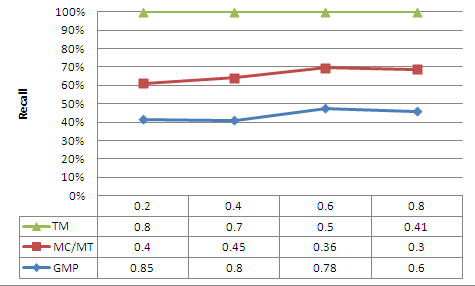Figure 8. Recall as a function of the corruption factor

6. Conclusions

In this paper, we applied a data mining technique for the prediction of behavioural group patterns derived from user movements’ data in a mobile computing system. The algorithm proposed in this study is based on mining the mobility patterns of users in each group, forming mobility rules from these patterns, and finally predicting a mobile user’s group movements using the mentioned mobility rules. Through accurate prediction of mobile user movements, our algorithm enabled the system to allocate resources to users in an efficient way, thus leading to an improvement in resource utilization and a reduction in the latency in accessing the resources. Furthermore, our algorithm enabled the system to produce more accurate answers to location dependent queries that refer to future positions of mobile users. We have evaluated the performance of our algorithm using simulation and compared the obtained results with the performance of two other prediction methods, mobility prediction based on MC/MT and TM models. In MC/MT model, mobility prediction is based on the cell-to-cell transition probability matrix. The TM method does not take any historical information into account when making prediction. In this method, randomly selected neighbours of the current cell are used as the predicted cells. This method can be considered as a baseline algorithm for comparison. Our method has performed well with a variety of corruption factor and outlier percentage values. We have observed that although an increase in the corruption in the data decreases the recall and precision, an increase in the outlier percentage has no significant effect on the recall and precision. When compared to the performance of the baseline method, which is MC/MT Prediction, our method provides a very good performance in terms of precision and recall.

APPENDIX

Present the three tables as 1) Database of group actual paths (gaps), 2) Generating all possible mobility rules and 3) The set of all large patterns.

Table 2. Database of group actual paths (GAPS)

Table 3. Generating all possible mobility rules

Table 4. The set of all large patterns PATTERN SUPP PATTERN SUPP 0 4 0, 3 1.33 2 2 3, 4 2 3 3 4, 0 1.5 4 3 4, 5 2.5 5 3 5, 0 1.5 0,5 1.5 3, 4, 0 1.5 2,0 1.33 3, 4, 5 1.5

ACKNOWLEDGEMENTS

The authors would like to thank the anonymous reviewers for their valuable feedbacks and suggestions for this work. We would also like to acknowledge support from the Graduate School of Information Technology at Siam University.