1. Introduction

The study results of the mechanism of actinides photofission reactions and their characteristics provide essential information about the properties of atomic nuclei since the nature of the photon-induced interactions is well known and allows obtaining fissionable nuclei directly after their absorption [1,2]. In addition, the information on the yields of actinides photofission products (fragments, prompt, and delayed neutrons) is relevant for solving a wide range of applied problems. These tasks are related to the development of new-generation energy-generating systems ‒ reactors with accelerators (controlled subcritical systems [3]), non-destructive methods of isotopic analysis of fertile nuclear materials [4,5], and alternative methods of developing medical radioisotopes [5]. The above-mentioned directions require reliable data on the yields of actinide photodissociation products.

Bremsstrahlung radiation obtained at electron accelerators is widely used to stimulate the actinides photofission reaction [2,4-6]. The bremsstrahlung photons and their energy spectra, obtained by converting electron beams into bremsstrahlung radiation (the generation process of which occurs due to radiative braking of electrons), depending on the initial energy of the electrons and the nuclear-physical properties of the materials from which the converters (converters of electron radiation into photons) are made [7-9]. Also, the bremsstrahlung photons and their energy spectra are affected by the geometric size of the initial electron beams (geometric shape of the cross-section in the beam plane, their distribution in space) and converters [10,11].

Since the optimal thickness of the converters (when the output of bremsstrahlung photons is maximum) is less than the electron’s mean free path in the substance from which the converter is made [12], there will be residual electrons in the beams of bremsstrahlung radiation [13,14].

Residual electrons, when interacting with the studied actinide samples, can generate secondary photons [15] and photoneutrons [16,17] in them, as well as additionally stimulate electronuclear and photonuclear reactions [18] and cause damage to the samples due to their heating (thermalization). In addition, secondary photoneutrons will be present in the bremsstrahlung beam formed in the converter material through e → γ → n reaction channels [19]. These factors can significantly affect the results of studies of the actinides’ photofission characteristics.

Thus, when the activation schemes of samples on electronic accelerators do not use magnets to remove electrons that have passed through the Ta-converter [20,21], there is a need to "clean" bremsstrahlung beams from residual electrons and secondary photoneutrons.

For "cleaning" bremsstrahlung beam without significantly weakening the intensity of photons, filters are used, which are made of materials with a small atomic number such as reactor graphite, aluminum, and boron carbide [13,22,23].

It should be noted that the quantitative (integral) number of photons, residual electrons, and secondary photoneutrons and their ratio in the bremsstrahlung beams that interact with the studied actinide samples are significantly influenced by geometric factors (the location of the converters and the studied samples relative to the electron output node of the accelerator), and the presence of additional structural elements (filters, screens, collimators), which are used in their formation [24]. Also, the final parameters of the bremsstrahlung beams will be influenced by the design features of the devices (assemblies) ‒ their output node, which differ significantly for different types of electron accelerators [25]. Therefore, these factors must be taken into account when developing actinide sample activation schemes.

To optimize the schemes (conditions) of irradiation of actinide samples by electron accelerators, it is necessary to have complete and reliable information about the characteristics of the bremsstrahlung beam and its components (photons, residual electrons, photoneutrons) that determine the radiation field of the beam and associated particles. Comprehensive information about the radiation fields is contained in the energy distributions of the bremsstrahlung components if they are known for any angle of photon emission from the target for the three-dimensional distribution relative to the axis of the electron beam.

Conducting experimental studies of the characteristics of the bremsstrahlung spectra, residual electrons, secondary photoneutrons, and their integral values (for example, with activation and tracking detectors, TLD dosimeters, and proportional counters [26,27]) is associated with significant difficulties (expensive and long-term measurements) and in many cases practically impossible.

To obtain information about the characteristics of bremsstrahlung beams obtained at electronic accelerators that interact with the studied samples, taking into account their design features and irradiation schemes, computer modeling using Monte Carlo software codes (MCNP6, FLUKA, GEANT4 [28,29]) is widely used, as they make it possible to obtain the spectra of bremsstrahlung photons, residual electrons, and secondary photoneutrons as closely as possible to the real conditions of their formation.

The presented work aims to model the optimal scheme for stimulation of the actinides’ photofission reaction on the electron accelerator of the Institute of Electronic Physics of the National Academy of Sciences (IEP NAS) of Ukraine - microtron M-30, taking into account the technical characteristics of its output node.

2. Materials and Methods

A software application was developed for modeling the photon spectra, residual electrons, and secondary photoneutrons, which were formed during the interaction of electrons with the Ta-converter and hit the plane (area in the location of the investigated actinide samples) or the samples themselves, installed perpendicular to the beam axis of the primary electron beam. The application was implemented in C++ using the GEANT4 10.7.1 toolkit [30,31]. The choice of the specified toolkit was determined by its suitability for modeling the formation processes of various types of particles and their interaction with the studied samples on electronic accelerators [2,9,28], as well as its availability in terms of free use.

The developed application gave a possibility to implement various variants of actinide activation schemes by taking into account the installation of structural elements (converters, filters, samples) in the three-dimensional space given by the input data. The simulation results of the activation process according to the given schemes made it possible to visualize the images of the profiles of all photons and electrons that hit the plane at the location of the studied actinide sample.

This made it possible to reproduce real irradiation schemes of the investigated actinide samples for implementation on electronic accelerators (in this case, on the electronic accelerator of the IEP of NAS of Ukraine - the M-30 microtron [26]).

The application was created for the Windows platform using multi-threading mode. A computer with a 6-core Intel (R) Core (TM) i7-9750H (2.60 GHz) processor and 36 GB of RAM was used for calculations. With the specified material base, calculations were made for the number of 1E8 events ÷ 1E9. The average calculation time was ~ 8-10 hours.

Calculations were made for 17.5 MeV electron energy. The output electron beam had the shape of an ellipse with axes of 22 × 6 mm and an equally probable distribution (taking into account the design features of the electron output node - a titanium window with a thickness of 0.05 mm) [32,33].

Figure 1 shows the scheme of stimulation of actinide photofission reaction by the M-30 microtron, where 1. is the output node of the M-30 microtron; 2. Ti-window; 3. Ta-converter; 4. filter (diameter – 35 mm, thickness – 19 mm); 5. a sample of actinide. Additionally, the photo of the output node is presented. The distance from the output node to the tantalum (Ta) converter was 22 mm.

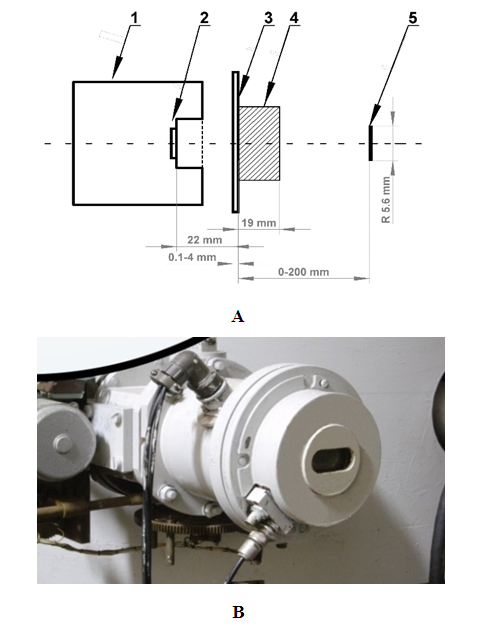Figure 1. Scheme of stimulation of the photodissociation reaction of actinides on the M-30 microtron (A) and photo of its output node (B)

Calculations were made for the Ta-converter with the following shapes: rectangular plate 100 × 50 mm with a thickness of 0.1, 0.5, 1.0, 1.5, 2.0, 3.0, 4.0 mm, and a cylinder with a thickness of 1 mm and a radius of 10, 15, 20, 30, 50, and 100 mm.

The actinide sample had the shape of a cylinder with a radius of 5.6 mm. Calculations were carried out for fixed distances of 0, 25, 50, 75, 100, 125, 150, 175, and 200 mm from the Ta-converter to the test sample installed perpendicular to the beam axis.

3. Results and Discussion

Simulations were carried out on the effect of the Ta-converter thickness (from 0.1 to 4 mm) on the characteristics of the bremsstrahlung spectra at a fixed distance from the converter to the place of sample installation of 75 mm. As a sensitive detector, a plane with the size of 1000x1000 mm and a cylinder corresponding to the dimensions of the real test sample were taken.

The spectra of bremsstrahlung photons and residual electrons interacting with the plane were obtained in the result of modeling and are shown in Figures 2 and 3. Similarly, the spectra of photons and electrons interacting with the real target are shown in Figures 4 and 5.

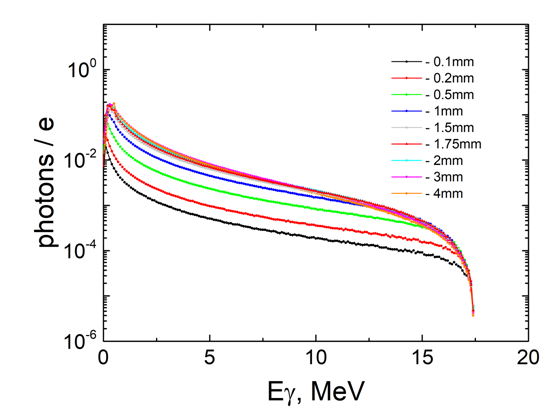Figure 2. Bremsstrahlung spectra for different thicknesses of the Ta-converter that hit the plane

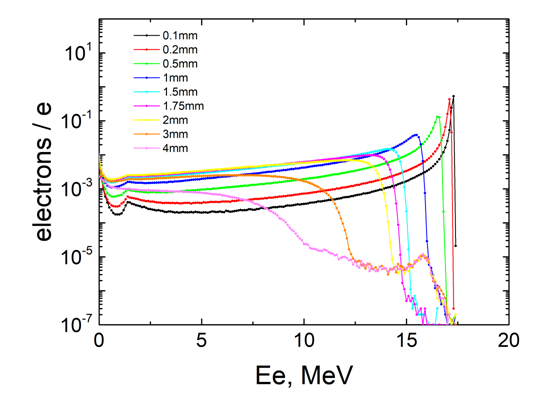Figure 3. Spectra of the residual electrons for different thicknesses of the Ta-converter that hit the plane

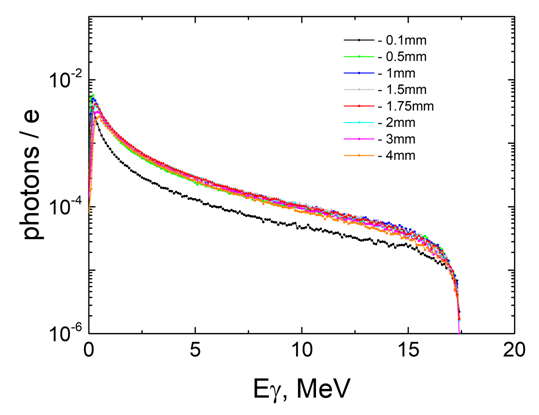Figure 4. Bremsstrahlung spectra for different thicknesses of the Ta-converter that hit the real actinide sample

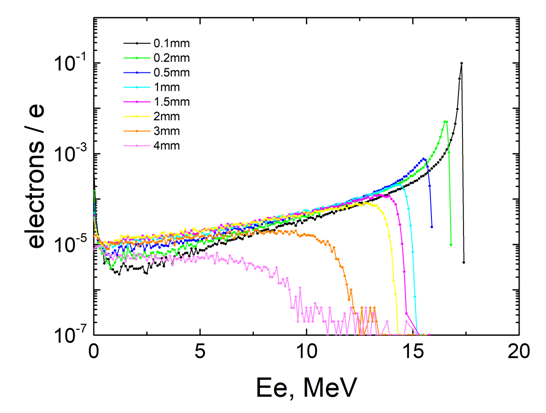Figure 5. Spectra of the residual electrons for different thicknesses of the Ta-converter that hit the real actinide sample

All results are normalized to one electron of the initial electron beam.

From the spectra of bremsstrahlung photons and residual electrons obtained as a result of simulation, integral values of the entire spectrum and its part for the energy range from 6 to 17.5 MeV were calculated. In this energy range, bremsstrahlung photons stimulate the photofission reaction of actinides, and residual electrons can additionally generate secondary photons and photoneutrons in the sample. Graphs of the dependence of the integral values of spectra of bremsstrahlung photons and residual electrons on the thickness of the Ta-converter are shown in Figures 6 and 7, respectively.

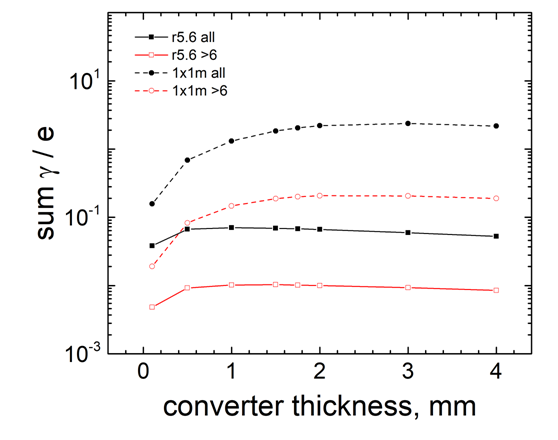Figure 6. Dependence of the integral values of bremsstrahlung photons on the thickness of the Ta-converter that hit the plane and the studied sample

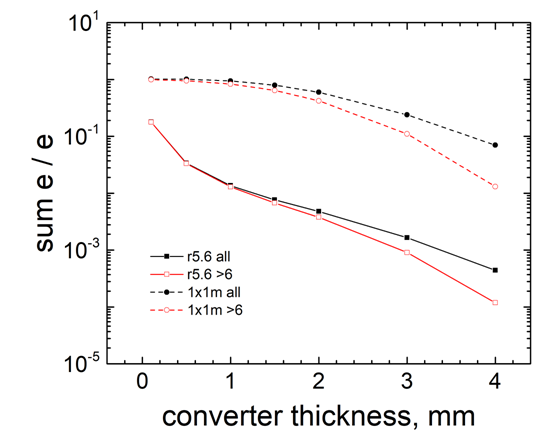Figure 7. Dependence of the integral values of the residual electrons on the thickness of the Ta-converter that hit the plane and the studied sample

With an increase in the thickness of the Ta-converter to ~ 1.0 mm, the integral values of the photon spectra interacting with the real sample (normalized by 1 e) increase and reach a maximum value of 0.07067. With a further increase in thickness to 4 mm - the values are constant. For photons with energies ≥ 6 MeV, the maximum yield of bremsstrahlung photons is reached at a thickness of ~ 1 mm (0.01022).

The ratio of the integral values of whole residual electron spectra and its part with energies from 6 to 17.5 MeV that hit the actinide sample (normalized to 1 e) also depends on the thickness of the Ta-converter. As the thickness of the converter increases from 0.1 to 4 mm, the integral values of all residual electrons decrease from 0.17843 to 4.416E-4. At a thickness of 1 mm, the value is 0.01364. For residual electrons with energies ≥ 6 MeV, the values change from 0.1776 to 1.181E-4. At a thickness of 1 mm, the value is 0.01293.

Further calculations were carried out for a fixed thickness of the Ta-converter, which was equal to 1 mm (at this thickness, the maximum output of photons is achieved).

When studying the dependence of the bremsstrahlung spectra's characteristics on the converter's geometric size, the technical characteristics of the output node of the M-30 microtron were taken into account [32,33]. Thus, the radius of the converter was taken from 5 mm to 25 mm at a fixed distance from the converter to the place of sample installation of 75 mm.

The spectra of bremsstrahlung photons and residual electrons interacting with the plane obtained as a result of modeling are shown in Figures 8 and 9. Similarly, the spectra of photons and electrons interacting with the real target are shown in Figures 10 and 11.

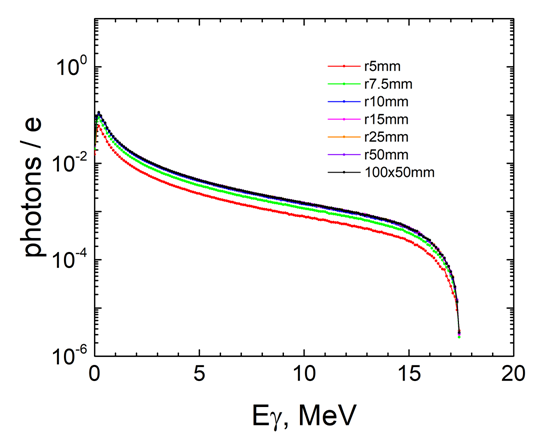Figure 8. Bremsstrahlung spectra for different radii of the Ta-converter that hit the plane

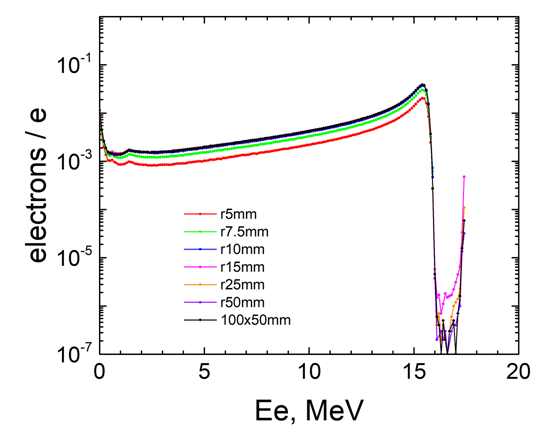Figure 9. Spectra of the residual electrons for different radii of the Ta-converter that hit the plane

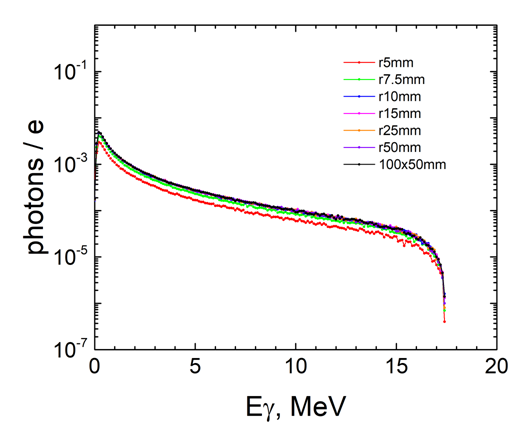Figure 10. Bremsstrahlung spectra for different radii of the Ta-converter that hit the real actinide sample

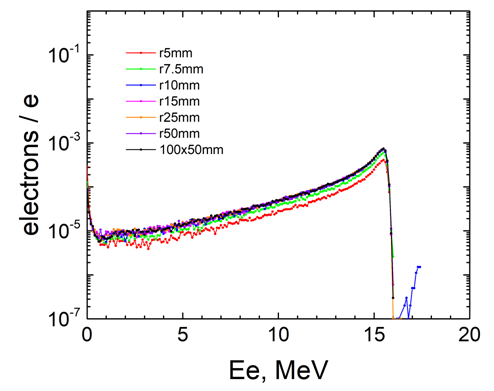Figure 11. Spectra of the residual electrons for different radii of the Ta-converter that hit the real actinide sample

Dependence of the integral values of bremsstrahlung photons and residual electrons (for the entire spectrum and with energies from 6 to 17.5 MeV) on the radius of the Ta-converter, which hit the plane and the real actinide sample (Figures 12, 13), are established.

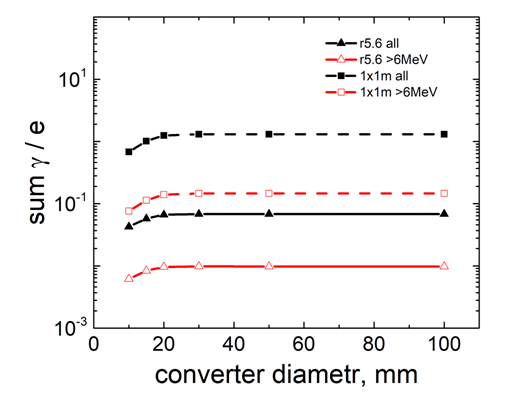Figure 12. Dependence of the integral values of bremsstrahlung photon spectra on the radius of the Ta-converter (thickness 1 mm) that hit the plane and the real actinide sample

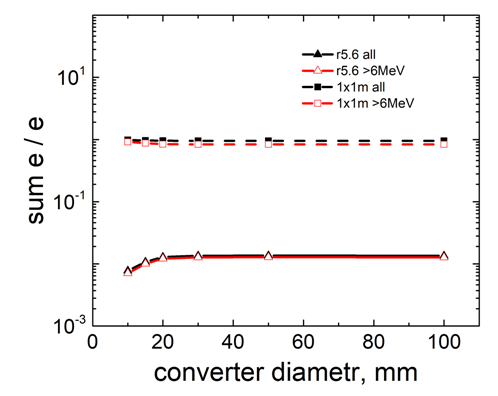Figure 13. Dependence of the integral values of residual electron spectra on the radius of the Ta-converter (thickness 1 mm) that hit the plane and the real actinide sample

Given that the area of the Ta-converter is larger than the geometric size of the initial electron beam, the size and shape of the converter do not affect the integral values of the generated bremsstrahlung photons and residual electrons. Therefore, the choice of the geometric size of the converter (100 x 50 mm) was due to the design features of the electron output node into the air and ease of use.

Calculation results of the dependence of the spectra of bremsstrahlung photons and residual electrons (normalized by 1 e) that hit the studied sample on the distance Ta-converter - sample (0 ÷ 200 mm) at a fixed thickness of the Ta-converter = 1 mm are presented in Figures 14 and 15, respectively.

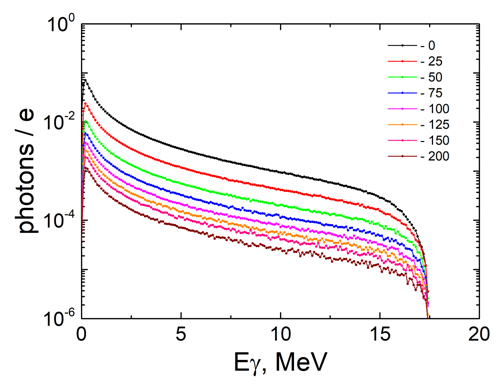Figure 14. Bremsstrahlung spectra for different distances of Ta-converter – sample

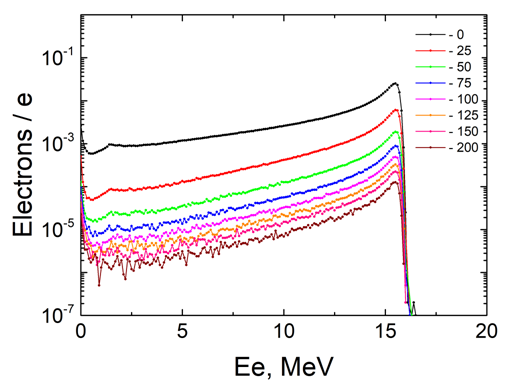Figure 15. Spectra of residual electrons for different distances of Ta-converter – sample

Based on the above calculations, integral values of bremsstrahlung photons and residual electrons hitting the real actinide sample were obtained (Figures 16, 17).

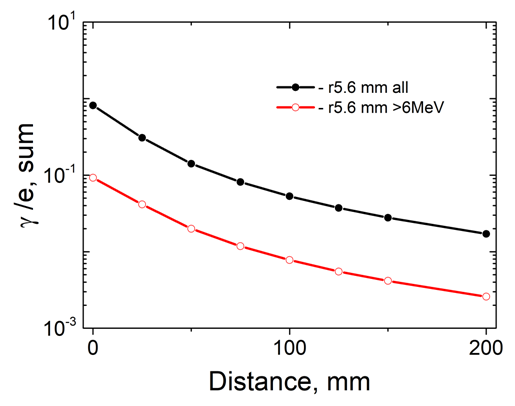Figure 16. Dependences of the integral values of bremsstrahlung photon spectra on the distance Ta-converter – sample

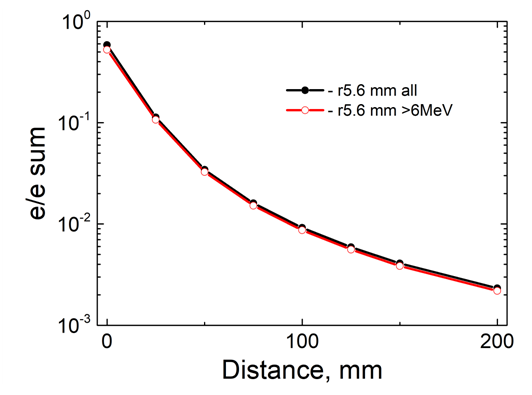Figure 17. Dependences of integral values of residual electron spectra on the distance Ta-converter – sample

It was established that the integral values of the spectra of the bremsstrahlung photons (Figure 16) and residual electrons (Figure 17) depend on the distance. With its increase from 0 to 200 mm, the integral values of photons and residual electrons spectra decrease from 0.81332 to 0.01711 (from 0.09218 to 0.00258 at energy ≥ 6 MeV) and from 0.58449 to 0.00233 (from 0.52531 to 0.00218 at energy ≥ 6 MeV), respectively.

In addition, calculations of the photoneutron spectra (normalized by 1 e) that interact with the actinide sample were carried out for the Ta-converter-sample distances (0 - 200 mm) at a fixed thickness of the Ta-converter = 1 mm (Figure 18).

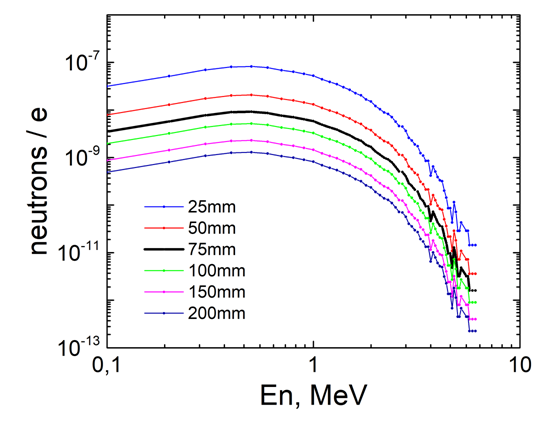Figure 18. Photoneutron spectra for different distances of Ta-converter – sample

As a result of the calculations, the dependence of the integral values of photoneutrons (for the entire energy spectrum) on the distance Ta-converter ‒ sample, that interact with the studied actinide, sample was established (Fig. 19).

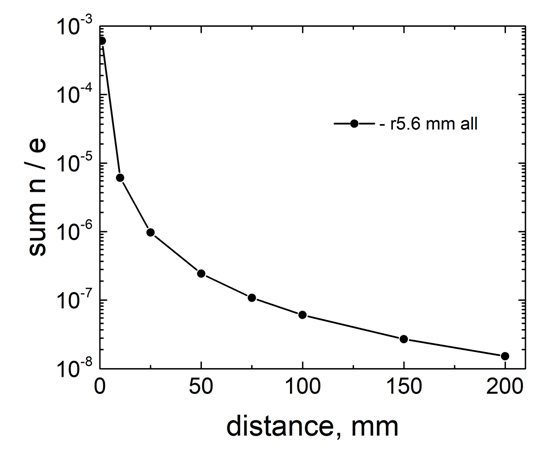Figure 19. Dependencies of the integral value of photoneutrons on the distance Ta-converter – sample

As the distance increases from 0 to 200 mm, the integral values of photoneutrons decrease from 6.08254E-4 to 1.52063E-8.

At a distance of 75 mm, the integral value of bremsstrahlung photon spectra equals 0.01179, which is less than ~ 8 times compared to their value when the sample is installed close to the Ta-converter. With a further increase in the distance (from 75 to 200 mm), the number of bremsstrahlung photons decreases by ~4.5 times.

At a distance of 75 mm, the integral value of residual electron spectra equals 0.01518, which is ~ 35 times less than their value when the sample is installed close to the Ta-converter. With a further increase in the distance (from 75 to 200 mm), the number of residual electrons decreases by only ~ 6.5 times.

At a distance of 75 mm, the integral value of photoneutrons equals 1.08134E-7, which is 4 orders of magnitude less than their value when the sample is installed close to the converter. With a further increase in the distance (from 75 to 200 mm), the number of neutrons decreases by only 1 order of magnitude.

Thus, at a distance of 75 mm, with a thickness of 1 mm and a size of the Ta-converter - 100 x 50 mm, there is a significant decrease in the integral values of the residual electrons and secondary photoneutrons with a slight decrease in the integral values of bremsstrahlung photons (energy spectrum from 6 to 17.5 MeV).

The calculations made it possible to establish the optimal geometric size and shape of the Ta-converter (100 x 50 x 1 mm) and the distance from the Ta-converter to the actinide sample (75 mm) for the formation of a bremsstrahlung beam on the M-30 microtron, taking into account its design features of the electron output node.

The obtained results reproduce the general patterns of the formation of bremsstrahlung photons during the interaction of electrons with converters, namely, the dependence of their yield on the converter material and geometric dimensions, and are consistent with the results of similar studies [8,9,16].

It should be noted that when using such an actinide sample activation scheme, it is necessary to clean the bremsstrahlung beam from residual electrons that pass through the Ta-converter [13,22]. Since our experimental scheme does not use a deflecting magnet to divert the electrons that have passed through the Ta-converter, it becomes necessary to use a filter to clean the bremsstrahlung beam. However, the disadvantage of such a scheme when using traditional reactor graphite and aluminum filters is the additional generation of photoneutrons (of a broad energy spectrum from thermal to prompt), which can stimulate additional neutron reactions in the studied actinide samples. Unlike traditional filters made of reactor graphite and aluminum, filters made of boron carbide absorb slow (thermal and epi-thermal) neutrons [22].

Therefore, calculations were made of the components of the bremsstrahlung beam (photons, residual electrons, photoneutrons) that interacted with the studied actinide samples when B₄C was used as a filter. Additionally, for comparison, similar calculations were made for reactor graphite and aluminum filters.

The results of calculations of the spectra of bremsstrahlung photons, residual electrons, and photoneutrons (normalized to 1 e) interacting with the studied sample in the presence and absence of a B₄C filter at a fixed distance Ta-converter (thickness - 1 mm) - sample - 75 mm are given in Figures 2022, respectively.

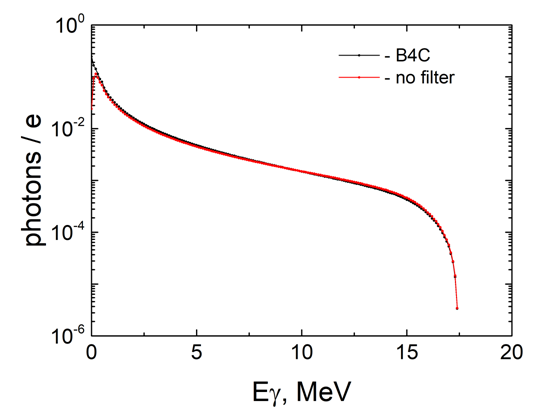Figure 20. Bremsstrahlung spectra interacting with the sample without and with the B4C filter

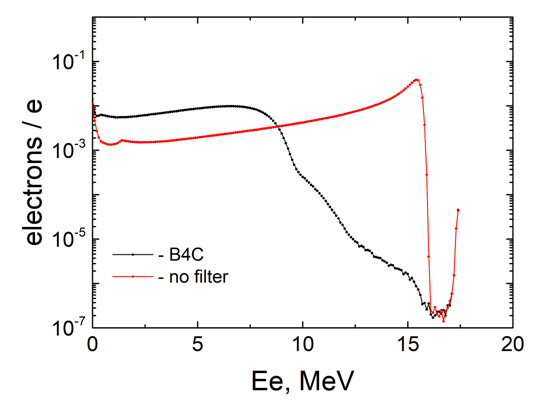Figure 21. Spectra of residual electrons interacting with the sample without and with the B4C filter

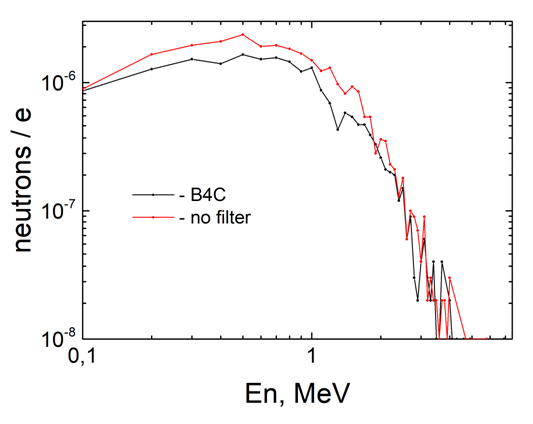Figure 22. Spectra of photoneutrons interacting with the sample without and with the B4C filter

It was established that the total number of residual electrons, photons, and photoneutrons absorbed by the filter made of B₄C is 43.64% (with energies ≥ 6 MeV – 70.17%), 13.07% (≥ 6 MeV – 6.38%) and 9.6%, respectively.

Additional calculations for reactor graphite and aluminum filters were carried out for an actinide sample activation scheme similar to the one with the B₄C filter. The geometric size of the filters made of reactor graphite and aluminum corresponded to the geometric size of the filter made of B₄C.

Calculated spectra of bremsstrahlung photons, residual electrons, and secondary photoneutrons (normalized to 1 e) interacting with the studied actinide sample in the presence and absence of various filters (aluminum, B₄C, and reactor graphite) at a fixed distance Ta-converter (thickness – 1 mm) – the studied sample = 75 mm, presented in Figures 23-25.

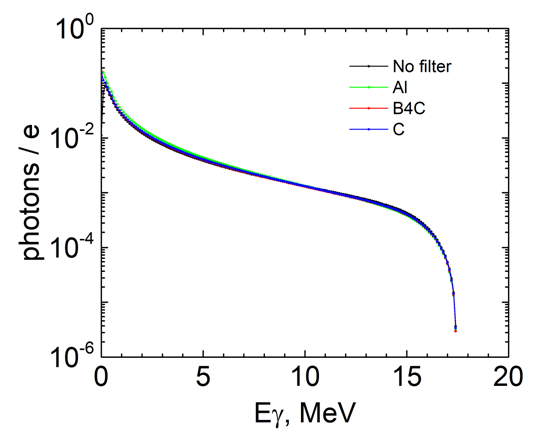Figure 23. Bremsstrahlung spectra interacting with the sample without and with various filters

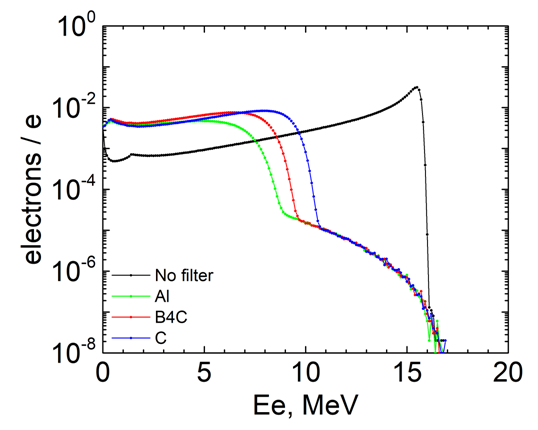Figure 24. Spectra of residual electrons interacting with the sample without and with various filters

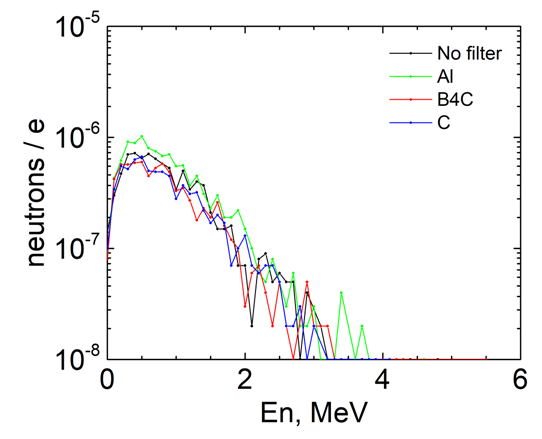Figure 25. Spectra of photoneutrons interacting with the sample without and with various filters

According to the results of calculations, it was established that B₄C absorbs residual electrons better than reactor graphite (70.17% and 57.12%, respectively). Compared to aluminum, its absorption properties are worse (70.17% and 91.39%), but aluminum generates additional photoneutrons (26.25%).

Based on the calculations, the parameters of the optimal scheme for stimulation of the actinide photodissociation reaction on the M-30 microtron were established, taking into account the technical features of its electron output unit, and studied sample characteristics.

Thus, the actinide activation scheme consists of a Ta-converter (1 mm thick) and a filter made of B₄C. The distance from the Ta-converter to the studied sample is 75 mm.

Figures 26 and 27 show the profiles of photons and electrons hitting the plane (1000 x 1000 mm) in the studied sample installation position.

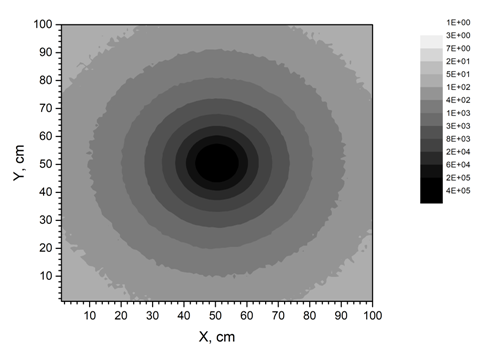Figure 26. Profile of a beam of residual electrons that hit the plane

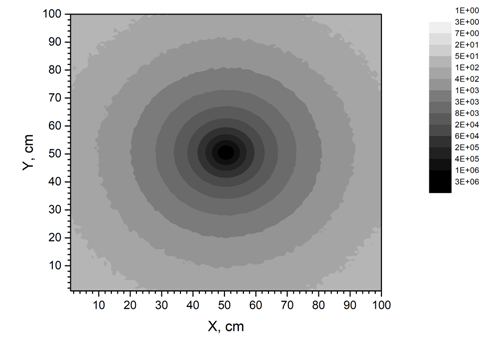Figure 27. Profile of a beam of photons that hit the plane

The ratio of the integral values of the spectra of bremsstrahlung photons, residual electrons, and photoneutrons that hit the real actinide sample to those that hit the plane is 6.38% (with energies ≥ 6 MeV – 11.12%), 2.59% (with energies ≥ 6 MeV – 3.99%) and 0.81%, respectively.

Thus, the presented scheme makes it possible to almost completely exclude the interaction of residual electrons and secondary photoneutrons with the studied actinide samples, that is, to make it impossible to stimulate additional electronuclear ((e,γ)-, (e,n)-, (e,f)-) and neutron ((n,γ)-, (n,f)-) reactions [34], which can contribute additional errors into the final results when studying the characteristics of actinide photofission reactions.

4. Conclusions

Conducted theoretical calculations using the GEANT 4 toolkit made it possible to establish the optimal parameters of the stimulation scheme for the photofission reactions of actinide samples on the M-30 microtron electron accelerator using a combined Ta + B₄C target. The obtained information is necessary for the formation of bremsstrahlung beams with the maximum number of photons and the minimum number of residual electrons and secondary photoneutrons, which interact with the studied actinide samples, and that takes into account the geometric sizes of the elements of the activation scheme (converters, filters) and their location, as well as the design features of the electron output node of the M-30 microtron.

This approach can be used for the development of actinide activation schemes in the study of their nuclear-physical characteristics, as well as for a wide range of applied applications: photonuclear activation analysis of the isotopic composition of fertile and fissile nuclear materials, transmutation of spent nuclear fuel, alternative production of medical radioisotopes on various types of electronic accelerators.

Funding

The present work was partially carried out within the framework of the project of research works of young scientists of the National Academy of Sciences of Ukraine. State registration number – 0123U102958).