-
Paper Information
- Paper Submission
-
Journal Information
- About This Journal
- Editorial Board
- Current Issue
- Archive
- Author Guidelines
- Contact Us
Journal of Nuclear and Particle Physics
p-ISSN: 2167-6895 e-ISSN: 2167-6909
2021; 11(3): 67-75
doi:10.5923/j.jnpp.20211103.02
Received: Dec. 4, 2021; Accepted: Dec. 22, 2021; Published: Dec. 24, 2021

The Effect of Pauli Operator on Nuclear Matter Properties within BHF Approach Using Argonne V18 Interaction
B. M. Elyan , A. E. Elmeshneb, Kh. S. A. Hassaneen
Faculty of Science, Physics Department, Sohag University, Egypt
Correspondence to: B. M. Elyan , Faculty of Science, Physics Department, Sohag University, Egypt.
| Email: |  |
Copyright © 2021 The Author(s). Published by Scientific & Academic Publishing.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/

We have studied the equation of state (EOS) and the contribution of partial waves for symmetric nuclear matter (SNM) and pure neutron matter (PNM) to explain the effect of Pauli operator treatment. Our calculations have been carried out in the framework of Bruckner-Hartree-Fock (BHF) approach with angle average approximation and exact Pauli operator using Argonne V18 nucleon-nucleon interaction. From studying the partial waves contributions to the equation of state (EOS), we have explained the effect of the tensor force. The correct saturation point is still missed, so the considered model needs to a correction to be able to reproduce the empirical saturation point of symmetric nuclear matter.
Keywords: BHF approach, Symmetric nuclear matter, Pure neutron matter, Angle average approximation, Exact Pauli operator, Single particle potential, Equation of state
Cite this paper: B. M. Elyan , A. E. Elmeshneb, Kh. S. A. Hassaneen , The Effect of Pauli Operator on Nuclear Matter Properties within BHF Approach Using Argonne V18 Interaction, Journal of Nuclear and Particle Physics, Vol. 11 No. 3, 2021, pp. 67-75. doi: 10.5923/j.jnpp.20211103.02.
Article Outline
1. Introduction
- Different many body theories have been developed to understand the properties of the nuclear matter like the many body perturbation theory [1-5], the Monte Carlo method with it's various versions [6-10], the variational method [11,12], and Bruckner-Hartree-Fock (BHF) approach [13,14].BHF approach considers that the nucleons in nuclear matter move in a mean field arising from the interaction with all other nucleons (bound nuclear matter) and have overcame the difficulty of the treatment of the strong short-range repulsive core for the nucleon-nucleon (NN) interaction which makes nuclear system non-perturbative. Brueckner and others [15,16] developed the G-matrix method which called Brueckner-Bethe-Goldstone theory. The effect of the nuclear medium is taken into calculations via Pauli operator, which limits the allowed intermediate sates above Fermi level and the denominator of the two body propagator contains the self energy.The exact treatment of Pauli operator and of the energy denominator is essential for the calculations. The Pauli operator depends on the angles between the relative and the center of mass momenta of the two scattering nucleons besides the magnitude of them. This angular dependence makes a difficulty in the numerical computations due to the coupling among the partial waves. Schiller [17] and others [18,19] have studied the exact treatment of Pauli operator. To avoid the coupling among the partial waves, the Pauli operator and the two nucleon energies averaged over the angle between the relative and the center of mass momenta. This is called angle average approximation [20,21].One of the main aims of Brueckner-Bethe-Goldstone theory is to study the equation of state and reproduce the empirical saturation point. Tensor component of the NN interaction plays a central role in reproduction of the experimental phase shifts and responsible for the structure and the binding energy of the deuteron [22]. Discussing the effect of the tensor force on the equation of state is a main aim of this work as we will see below.For both symmetric nuclear matter and pure neutron matter, we have carried out our calculations in the framework of BHF approach in three cases. The first case is by using the angle average approximation with the continuous choice of the single particle potential, the second by using the conventional one and the third is by using the exact Pauli operator.BHF approach calculations depend on the choice of the single particle potential where the conventional choice considers a zero single particle energy above Fermi level [23], but the continuous choice assumes the self -consistent BHF potential extends above Fermi level, thus making the single particle potential a continuous function through the Fermi surface [24]. This continuous choice leads to an enhancement of correlation effects in the medium than the conventional one. The nucleon nucleon interaction employed in this work is Argonne
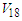 interaction [25].The Argonne
interaction [25].The Argonne 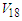 is non-relativistic potential defined in terms of local functions. It is with explicit charge dependence an charge symmetry. Wiringa et al. [25] have been updated Argonne
is non-relativistic potential defined in terms of local functions. It is with explicit charge dependence an charge symmetry. Wiringa et al. [25] have been updated Argonne 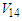 potential to fit both pp and np data with high quality. They added to the fourteen operators three additional charge-dependent and one charge-asymmetric operators. It called Argonne
potential to fit both pp and np data with high quality. They added to the fourteen operators three additional charge-dependent and one charge-asymmetric operators. It called Argonne 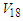 and it gives a
and it gives a 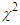 per datum 1.09 for 4301 pp and nn data in the range 0-350 MeV. The nucleon nucleon Argonne
per datum 1.09 for 4301 pp and nn data in the range 0-350 MeV. The nucleon nucleon Argonne 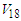 potential includes a complete electromagnetic part, one-pion-exchange (OPE) part and a short range phenomenological one.
potential includes a complete electromagnetic part, one-pion-exchange (OPE) part and a short range phenomenological one.2. The Theoretical Model
- The main component of BHF approach is the G-matrix which is defined by the Bethe-Goldstone equation as:
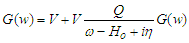 | (1) |
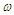 is the starting energy, V is the bare 2N potential,
is the starting energy, V is the bare 2N potential, 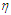 is a small number,
is a small number, 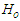 is the unperturbed energy of the intermediate states and Q is the Pauli operator which projects out states with two nucleons above the Fermi level and it's donated by the relation:
is the unperturbed energy of the intermediate states and Q is the Pauli operator which projects out states with two nucleons above the Fermi level and it's donated by the relation: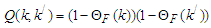 | (2) |
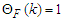 for
for 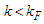 and zero otherwise and
and zero otherwise and 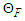 is the occupation probability of a free Fermi gas with a Fermi momentum
is the occupation probability of a free Fermi gas with a Fermi momentum 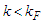 .According to BHF approach, the nuclear matter total energy is given by the expression:
.According to BHF approach, the nuclear matter total energy is given by the expression: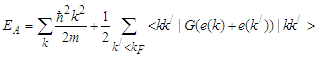 | (3) |
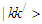 refer to the anti-symmetrization of the G-matrix elements. The single particle energy
refer to the anti-symmetrization of the G-matrix elements. The single particle energy 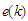 is the sum of the kinetic energy
is the sum of the kinetic energy 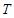 and the single particle potential
and the single particle potential 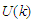 and given by:
and given by: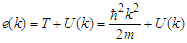 | (4) |
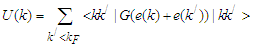 | (5) |
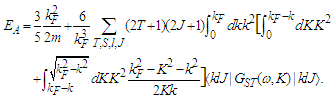 | (6) |
 is the angle between the direction of the relative momentum
is the angle between the direction of the relative momentum 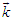 and the center of mass momentum
and the center of mass momentum 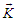 .And in the case of the exact of Pauli operator, it's given by:
.And in the case of the exact of Pauli operator, it's given by: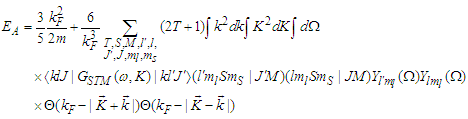 | (7) |
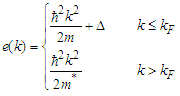 | (8) |
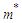 is the nucleon effective mass and
is the nucleon effective mass and  is a constant gives the single particle energy at k=0.The nuclear incompressibility
is a constant gives the single particle energy at k=0.The nuclear incompressibility 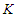 is an important characteristic of the nuclear matter equation of state (EOS) and it's related to the curvature of the energy per nucleon
is an important characteristic of the nuclear matter equation of state (EOS) and it's related to the curvature of the energy per nucleon 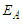 in symmetric nuclear matter around the saturation point by:
in symmetric nuclear matter around the saturation point by: 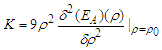 | (9) |
3. Results and Discussion
3.1. Single Particle Potential
- The single particle energy was represented by Eq. (4) as the sum of the kinetic energy
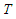 and the single particle potential
and the single particle potential 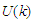 . As long as the kinetic energy is independent of the method of calculation, we will restrict our discussion on the single particle potential.In this work we have calculated the single particle potential
. As long as the kinetic energy is independent of the method of calculation, we will restrict our discussion on the single particle potential.In this work we have calculated the single particle potential 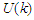 for symmetric nuclear matter and pure neutron matter according to eq.(5) using Argonne
for symmetric nuclear matter and pure neutron matter according to eq.(5) using Argonne 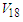 potential. The calculations have carried out with angle average approximation and exact Pauli operator. We plot the dependence of the single particle potential
potential. The calculations have carried out with angle average approximation and exact Pauli operator. We plot the dependence of the single particle potential 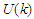 on the momentum
on the momentum 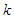 at different densities
at different densities 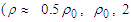
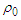 and
and 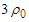 , where
, where 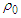 is the saturation density) in figs. (1) and (2) for the considered potential. The dotted curve represents the conventional choice which assumes a zero single particle potential for single-particle states above the Fermi level and U is self-consistent BHF potential for
is the saturation density) in figs. (1) and (2) for the considered potential. The dotted curve represents the conventional choice which assumes a zero single particle potential for single-particle states above the Fermi level and U is self-consistent BHF potential for 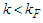 [26], the solid one represents the continuous choice for which the self-consistency of the BHF potential extends to
[26], the solid one represents the continuous choice for which the self-consistency of the BHF potential extends to 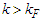 , and the dashed one represents exact Pauli operator. We notice that
, and the dashed one represents exact Pauli operator. We notice that 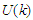 has a simple parabolic shape, increases with increasing
has a simple parabolic shape, increases with increasing  and the curve that represents the conventional choice is more repulsive than the other curves.
and the curve that represents the conventional choice is more repulsive than the other curves. | Figure 1. The single particle potential  as a function of momentum as a function of momentum 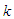 at different densities using Argonne at different densities using Argonne 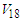 potential for symmetric nuclear matter potential for symmetric nuclear matter |
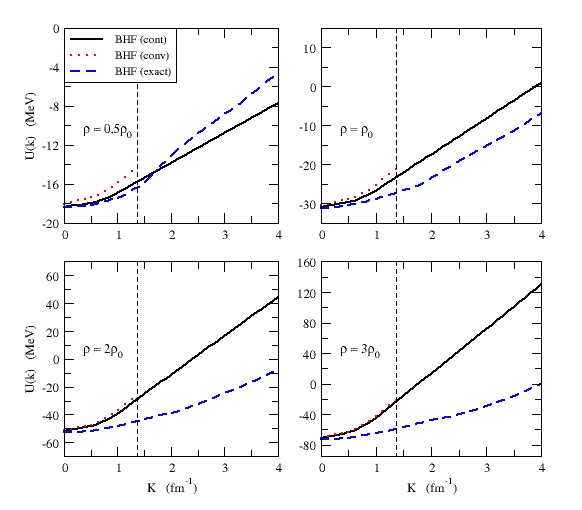 | Figure 2. The single particle potential 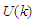 as a function of momentum as a function of momentum 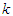 at different densities using Argonne at different densities using Argonne 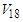 potential for pure neutron matter potential for pure neutron matter |
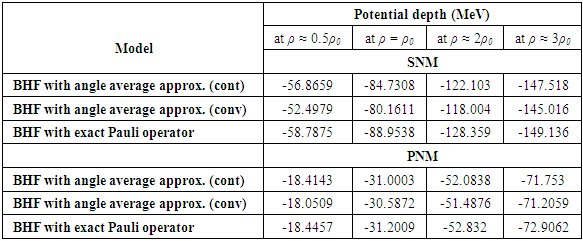
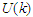 at
at 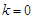 are listed in table (1) for symmetric nuclear matter and pure neutron matter. We notice that the potential depth decreases with increasing density. Also, it is more repulsive in the angle average approximation than the exact Pauli operator. That reflects the fact that the effective interaction is more attractive between nucleons in the exact Pauli operator than the angle average approximation [27]. When the density increases, the values of the single particle potential becomes more attractive at low momentum, and more repulsive at high momentum. Also, the difference between the values for the continuous choice and the conventional one decreases (the curves converge from each other), but the difference between the values for the angle average approximation and the exact Pauli operator increases (the curves diverge from each other).
are listed in table (1) for symmetric nuclear matter and pure neutron matter. We notice that the potential depth decreases with increasing density. Also, it is more repulsive in the angle average approximation than the exact Pauli operator. That reflects the fact that the effective interaction is more attractive between nucleons in the exact Pauli operator than the angle average approximation [27]. When the density increases, the values of the single particle potential becomes more attractive at low momentum, and more repulsive at high momentum. Also, the difference between the values for the continuous choice and the conventional one decreases (the curves converge from each other), but the difference between the values for the angle average approximation and the exact Pauli operator increases (the curves diverge from each other).
|
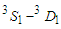 which increase the attraction. But at high momenta, the values of the single particle potential in symmetric nuclear matter more repulsive than that of pure neutron matter.
which increase the attraction. But at high momenta, the values of the single particle potential in symmetric nuclear matter more repulsive than that of pure neutron matter. 3.2. Partial Waves Contribution
- In this section, we will discuss the potential energy per nucleon originating from various partial waves up to J=9, where the contribution coming from higher partial waves is negligible. This contribution of the partial waves have studied using angle average approximation and exact Pauli operator without adding any correlations. The calculation carried out for symmetric nuclear matter and pure neutron matter using Argonne
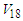 potential.Figs. (3) and (4) show the
potential.Figs. (3) and (4) show the 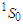 partial wave as a function of density
partial wave as a function of density 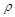 for symmetric nuclear matter and pure neutron matter, respectively. The value of
for symmetric nuclear matter and pure neutron matter, respectively. The value of 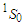 component in the three cases, the continuous choice (bold curve), the conventional one (dotted curve), and the exact Pauli operator (dashed curve) decreases with increasing density. But in the cases of exact Pauli operator, it decreases until reaches a minimum value then increases with increasing density. The curve that represents the exact Pauli operator is more repulsive than others, and this means the exact treatment of Pauli operator makes a significant change by inducing a substantial repulsion with increasing density.
component in the three cases, the continuous choice (bold curve), the conventional one (dotted curve), and the exact Pauli operator (dashed curve) decreases with increasing density. But in the cases of exact Pauli operator, it decreases until reaches a minimum value then increases with increasing density. The curve that represents the exact Pauli operator is more repulsive than others, and this means the exact treatment of Pauli operator makes a significant change by inducing a substantial repulsion with increasing density.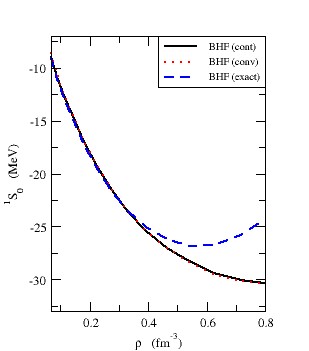 | Figure 3. The 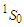 partial wave as a function of density partial wave as a function of density 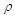 using Argonne using Argonne 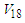 potential for symmetric nuclear matter potential for symmetric nuclear matter |
 | Figure 4. The 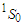 partial wave as a function of density partial wave as a function of density  using Argonne using Argonne 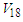 potential for pure neutron matter potential for pure neutron matter |
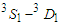 partial wave as a function of density
partial wave as a function of density 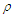 for symmetric nuclear matter in the above mentioned cases. This partial wave takes negative values only, therefore it's responsible for the bound state of the symmetric nuclear matter. This clarifies the absence of this component for pure neutron matter. The three cases have the same behavior, the
for symmetric nuclear matter in the above mentioned cases. This partial wave takes negative values only, therefore it's responsible for the bound state of the symmetric nuclear matter. This clarifies the absence of this component for pure neutron matter. The three cases have the same behavior, the 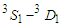 component value decreases with increasing density until reaches a minimum value then increases with increasing density. In the same figure we notice that the curve which represents the exact Pauli operator is more attractive at small densities than others, this is due to the enhancement of the tensor force. Tensor force is a very important source for the origin of the two-body correlations and originally is in a relative
component value decreases with increasing density until reaches a minimum value then increases with increasing density. In the same figure we notice that the curve which represents the exact Pauli operator is more attractive at small densities than others, this is due to the enhancement of the tensor force. Tensor force is a very important source for the origin of the two-body correlations and originally is in a relative 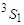 state with momentum below
state with momentum below 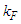 into a
into a 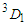 state above
state above 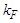 [27]. The measure of tensor force is called D-state probability
[27]. The measure of tensor force is called D-state probability 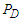 obtained for the deutron, which equals 5.76% for Argonne
obtained for the deutron, which equals 5.76% for Argonne 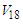 [28]. This large value of D-state probability for Argonne
[28]. This large value of D-state probability for Argonne 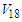 comparing with that for other NN interactions refers to the strong tensor force for Argonne
comparing with that for other NN interactions refers to the strong tensor force for Argonne 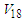 [29].
[29].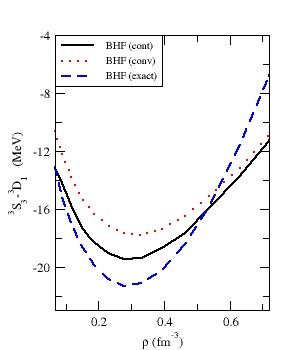 | Figure 5. The  partial wave as a function of using Argonne partial wave as a function of using Argonne 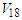 potential for symmetric nuclear matter potential for symmetric nuclear matter |
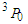 partial wave as a function of density
partial wave as a function of density 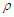 for symmetric nuclear matter and pure neutron matter, respectively. It's value decreases with increasing density until reaches a minimum value then increases with increasing density. The effect of the exact treatment is large at high densities, especially for pure neutron matter.
for symmetric nuclear matter and pure neutron matter, respectively. It's value decreases with increasing density until reaches a minimum value then increases with increasing density. The effect of the exact treatment is large at high densities, especially for pure neutron matter.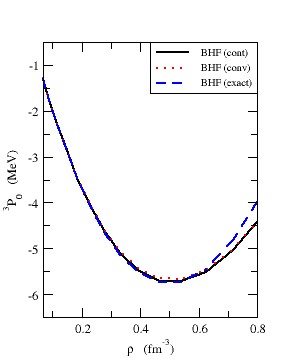 | Figure 6. The 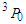 partial wave as a function of density partial wave as a function of density 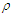 using Argonne using Argonne 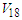 potential for symmetric nuclear matter potential for symmetric nuclear matter |
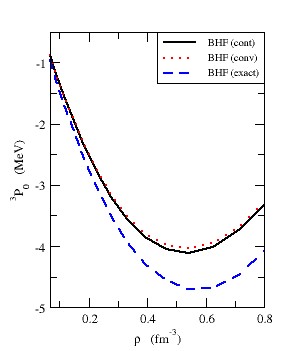 | Figure 7. The 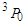 partial wave as a function of density partial wave as a function of density 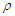 using Argonne using Argonne 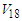 potential for pure neutron matter potential for pure neutron matter |
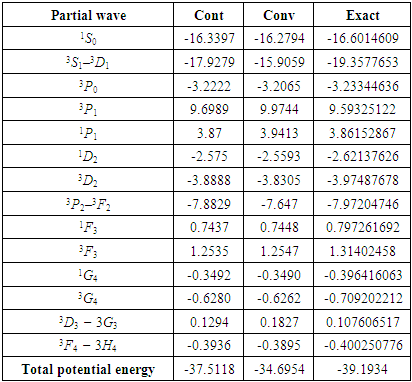
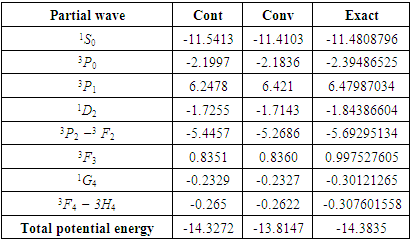
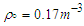 . Table (3) is the sam as (2) but for pure neutron matter. From this table, we can say
. Table (3) is the sam as (2) but for pure neutron matter. From this table, we can say 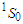 and
and 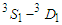 partials waves are more important than other partial waves and have the main contribution to EOS.
partials waves are more important than other partial waves and have the main contribution to EOS.
|
|
3.3. Equation of State
- The results of EOS calculations are plotted in fig. (8) for symmetric nuclear matter. The dotted curve represents the conventional choice, the solid one represents the continuous choice, and the dashed one represents the exact Pauli operator. The empirical saturation point indicated by square box, whereas the solid points refer to the calculated saturation points.
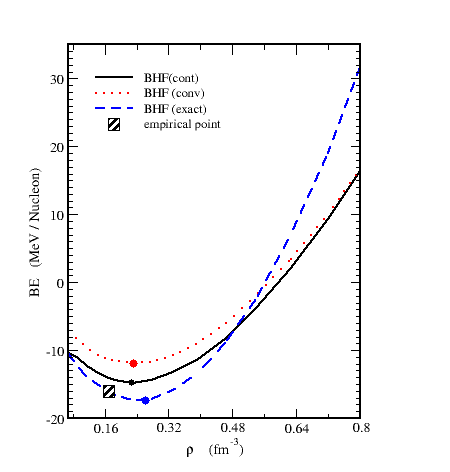 | Figure 8. The binding energy per nucleon E/A as a function of density 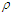 using Argonne using Argonne 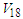 potential for symmetric nuclear matter potential for symmetric nuclear matter |
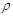 until reaches the saturation point, then it increases with increasing density
until reaches the saturation point, then it increases with increasing density 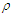 . The binding energy per particle
. The binding energy per particle 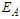 using Argonne
using Argonne 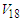 takes repulsive values. This means that the quenching effect, which reduces the interaction of non-Born terms in the G-matrix efficient for Argonne
takes repulsive values. This means that the quenching effect, which reduces the interaction of non-Born terms in the G-matrix efficient for Argonne 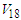 , consequently Argonne
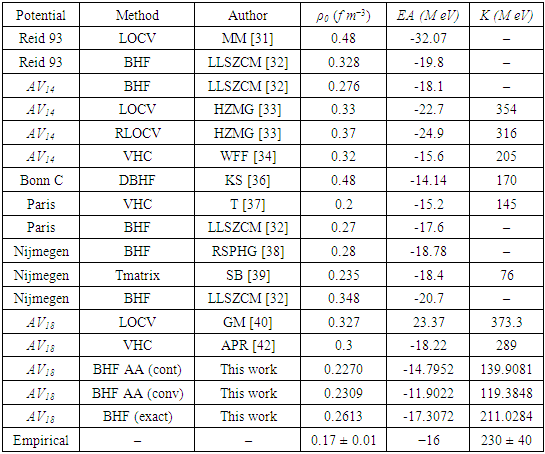
, consequently Argonne 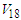 potential yield more repulsion compared to other potentials [27]. The curve that represents the exact treatment of Pauli operator is more attractive than other curves at low densities but is more repulsive at high densities. Table (4) shows the saturation points in the three cases for the considered potential. The saturation points are fallen on a band (called Coester band [30]) shifted with respect to the empirical saturation point
potential yield more repulsion compared to other potentials [27]. The curve that represents the exact treatment of Pauli operator is more attractive than other curves at low densities but is more repulsive at high densities. Table (4) shows the saturation points in the three cases for the considered potential. The saturation points are fallen on a band (called Coester band [30]) shifted with respect to the empirical saturation point 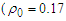
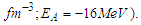 It's obvious that the saturation point in case of the exact treatment of Pauli operator and the continuous choice is closer to the empirical point than the conventional one. Therefore, the exact treatment of Pauli operator and the continuous choice lead to an enhancement of correlation effects and the exact treatment of Pauli operator predicts larger binding energy for nuclear matter. Fig. (9) shows the EOS results for pure neutron matter. The binding energy per nucleon takes positive values only which increases rapidly with increasing density. It's clear that the effect of exact treatment of Pauli operator is negligible.
It's obvious that the saturation point in case of the exact treatment of Pauli operator and the continuous choice is closer to the empirical point than the conventional one. Therefore, the exact treatment of Pauli operator and the continuous choice lead to an enhancement of correlation effects and the exact treatment of Pauli operator predicts larger binding energy for nuclear matter. Fig. (9) shows the EOS results for pure neutron matter. The binding energy per nucleon takes positive values only which increases rapidly with increasing density. It's clear that the effect of exact treatment of Pauli operator is negligible. | Figure 9. The binding energy per nucleon E/A as a function of density  using Argonne using Argonne 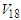 potential for pure neutron matter potential for pure neutron matter |
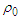 is
is 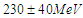 [43]. The calculated values of
[43]. The calculated values of 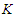 according to equation (9) for the considered cases using Argonne
according to equation (9) for the considered cases using Argonne 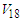 are listed in table (4). We observe that the value of
are listed in table (4). We observe that the value of 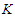 in the case of exact Pauli operator lies on the range of the experimental measurement. This refers to the good effect of the exact treatment of Pauli operator. A comparison of our nuclear matter binding energy, saturation density as well as incompressibility with other many-body methods for various potentials is also listed in table (4).
in the case of exact Pauli operator lies on the range of the experimental measurement. This refers to the good effect of the exact treatment of Pauli operator. A comparison of our nuclear matter binding energy, saturation density as well as incompressibility with other many-body methods for various potentials is also listed in table (4).
|
4. Conclusions
- From the above mentioned, we would like to show that the exact treatment of Pauli operator has a good enhancement in medium better than the angle average approximation. Tensor force effect appears by introducing the partial waves contributions, especially the
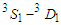 partial wave. The presence of
partial wave. The presence of 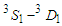 partial wave in symmetric nuclear matter (SNM) and it's absence in pure neutron matter (PNM) interpreted the unbound state for pure neutron matter (PNM).By using the exact treatment of Pauli operator, we have obtained a correct value of the incompressibility. But the effect of this treatment is not a very large around the empirical saturation point at small densities. Comparing our results with previous studies, we found that empirical saturation point is missed and we must add a correction to the present model to obtain the correct saturation point. This correction may be the three body forces which makes the results more repulsive.
partial wave in symmetric nuclear matter (SNM) and it's absence in pure neutron matter (PNM) interpreted the unbound state for pure neutron matter (PNM).By using the exact treatment of Pauli operator, we have obtained a correct value of the incompressibility. But the effect of this treatment is not a very large around the empirical saturation point at small densities. Comparing our results with previous studies, we found that empirical saturation point is missed and we must add a correction to the present model to obtain the correct saturation point. This correction may be the three body forces which makes the results more repulsive.  Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML