Cvavb Chandra Raju
Dept. Phys, Osmania University, Hyderabad, India
Correspondence to: Cvavb Chandra Raju, Dept. Phys, Osmania University, Hyderabad, India.
| Email: |  |
Copyright © 2021 The Author(s). Published by Scientific & Academic Publishing.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/

Abstract
The absolute mass eigen-states of the neutrinos and the absolute mass eigen states of the corresponding charged leptons are assumed to obtain their effective mass through their interaction with the Higgs field. However Electron and its neutrino of the Standard model have non-diagonal mass matrix. Similarly the muon and its neutrino have non-diagonal mass matrix. The Tau-lepton and its neutrino have a non-diagonal mass matrix in the Standard model. By diagonlizing these mass matrices, we can arrange a two flavor neutrino mixing. This mixing allows the estimation of the deviation of neutrino flux ratio from one flavor to the other flavor.
Keywords:
Neutrino mass eigenstates, Mass of charged lepton, Flavor mixing
Cite this paper: Cvavb Chandra Raju, Masses of the Neutrinos and Two Flavor Mixing, Journal of Nuclear and Particle Physics, Vol. 11 No. 2, 2021, pp. 47-51. doi: 10.5923/j.jnpp.20211102.03.
1. Introduction
The deviation of muon-neutrino flux to electron- neutrino flux is what is known as the Atmospheric neutrino anomaly. This observation of flavor violation is also observed by man made neutrinos after propagating sizable distances. To explain this, each neutrino flavor is assumed to be mixture of different mass eigenstates. As neutrinos propagate, each component mass eigen state acquires a different phase, so neutrino of a definite flavor will convert to a mixture different flavors. To obtain mixing It is the mass that causes mixing. we should consider three Neutrino mass and mixing scheme. Here we follow Two flavor mixing much like the Cabibbo-mixing in the quark sector.
2. Absolute Mass Eigenstates of Neutrinos and the Charged Leptons
The absolute value of the electron-neutrino mass comes from the Tritium beta decay [1] and appears to be about 2 eV. The muon neutrino also has mass. In the Standard Model [2] each lepton starts out with no intrinsic mass. The charged leptons obtain an effective mass through their interaction with the Higgs field. The neutrino is automatically massless because it is left-handed in the Standard model. Right-handed neutrinos have no interaction with other particles and so are not a functional part of the Standard Model. But neutrino oscillations confirm that Neutrinos have non-zero mass. Does the neutrino obtain its mass through interaction with the same Higgs field like all other particles? For this to take place we should start with a mass eigen state for the neutrino.Let there be a mass eigenstate for the electron neutrino and its effective mass be generated through the Lagrangian,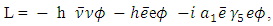 | (1) |
where, the Higgs field is 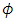 with the VEV
with the VEV 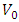 , and h in Eq. (1), is very small and we are not assuming that the neutrino is left-handed. It is a full mass eigenstate. The electron is coupled to the Higgs field through a
, and h in Eq. (1), is very small and we are not assuming that the neutrino is left-handed. It is a full mass eigenstate. The electron is coupled to the Higgs field through a 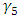 coupling also. We recover the standard model scenario when h is set zero and i
coupling also. We recover the standard model scenario when h is set zero and i 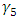 is replaced by one. Given a Dirac field say,
is replaced by one. Given a Dirac field say, 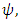 the Hermitian Scalar
the Hermitian Scalar 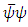 and
and 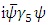 have opposite CP and T transformation properties (In this respect they are unlike the vector and axial vector.) The CP violation is now caused by the exchange of
have opposite CP and T transformation properties (In this respect they are unlike the vector and axial vector.) The CP violation is now caused by the exchange of 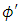 fields. Since the coupling of Higgs Field is usually rather small, it is possible to arrange for the CP violation to be of roughly milliweak magnitude [Mohapatra 1980, Bilenkey, 3&4].After spontaneous symmetry breaking from (1) we note that,
fields. Since the coupling of Higgs Field is usually rather small, it is possible to arrange for the CP violation to be of roughly milliweak magnitude [Mohapatra 1980, Bilenkey, 3&4].After spontaneous symmetry breaking from (1) we note that,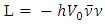
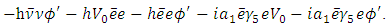 And with,
And with, 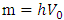 , which is now the electron-neutrino mass,
, which is now the electron-neutrino mass, 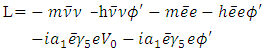 | (2) |
In the above m, and also h are presumably very small because m is neutrino mass. 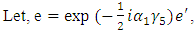 | (3) |
where 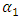 is a real parameter. Vector and axial vector interactions are not affected by this transformation. We choose
is a real parameter. Vector and axial vector interactions are not affected by this transformation. We choose 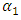 in such a way that the constant coefficient of
in such a way that the constant coefficient of 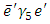 is zero. This gives,
is zero. This gives,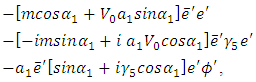 | (4) |
and set the coefficient of the second term equal to zero to yield, 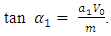 | (5) |
The mass of the electron is now given by,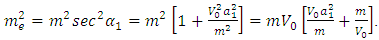 | (6) |
The very last term within the bracket is independent of the VEV. It is the sum of 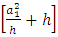 , which are the interaction constants of the Higgs field with the electron and its neutrino, [Eq.(2)]. Let,
, which are the interaction constants of the Higgs field with the electron and its neutrino, [Eq.(2)]. Let,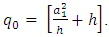 | (7) |
A similar Lagrangian can be chosen to obtain the effective mass for the muon and its neutrino through their interaction with the same Higgs field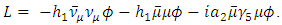 | (8) |
In Eq. (8), 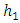 and
and 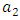 are real positive numbers and after symmetry breaking, the muon neutrino obtains the following mass:
are real positive numbers and after symmetry breaking, the muon neutrino obtains the following mass: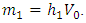 | (9) |
Following the same steps as in Eq. (2, 3, 4, and 5) for the Lagrangian (8) we readily observe that,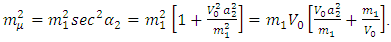 | (10) |
Again, we note that in Eq. (10) the parameter at the end in the brackets is independent of the VEV and is equal to 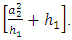 Let,
Let,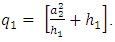 | (11) |
After symmetry breaking, the muon neutrino obtains the mass 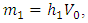 and with the same VEV,
and with the same VEV,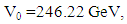 | (12) |
There is another massive charged lepton, the 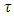 lepton. Its mass is,
lepton. Its mass is,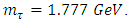 | (13) |
This lepton also has a neutrino. Like the other leptons, they start out with no intrinsic mass and obtain effective mass with their interaction to the same Higgs field with the VEV = V0. The Lagrangian in this case is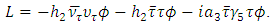 | (14) |
Following by now the familiar steps, after spontaneous symmetry breaking, we have, 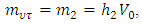 | (15) |
where 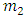 is the mass of the
is the mass of the 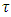 -neutrino and the mass of the charged
-neutrino and the mass of the charged 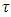 lepton is now given by,
lepton is now given by,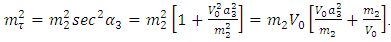 | (16) |
Again, the very last factor in the brackets is independent of the VEV.And it is given by, 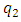 where,
where, 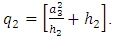 | (17) |
Even though we do not know what is the value of q, it is a real positive number. The masses of W and Z bosons are given in terms of the gauge constants gL and g’ of SU(2)L XU(1) through Higgs Mechanism. The mass generating interaction constants of the charged leptons with the Higgs boson are put by hand in the Standard model as there is no theory which will require a particular choice for these constants. In Eq. (2) the electron is coupled to the 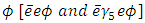 in two ways, and this sort of coupling is also there with the standard Z-boson. Using this clue, we tried to relate the masses of the electron and muon to the interaction constants
in two ways, and this sort of coupling is also there with the standard Z-boson. Using this clue, we tried to relate the masses of the electron and muon to the interaction constants 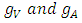 of the Z boson in Ref. [5].First let us note how a simple choice of
of the Z boson in Ref. [5].First let us note how a simple choice of 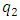 enables the prediction of Tau -neutrino mass.
enables the prediction of Tau -neutrino mass.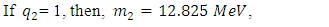 | (18) |
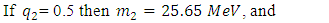 | (19) |
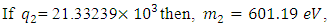 | (20) |
The choice of these values will be explained shortly. But it is clear that Neutrinos have mass. In the above, three possible values for the mass of the tau -neutrino are given. If h = h1 = h2 then all the three neutrinos will have the same mass. The electron neutrino mass can be computed from the following in which 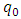 is chosen as a function of gauge constants [5].
is chosen as a function of gauge constants [5].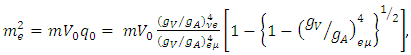 | (21) |
The factor 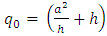 is given by the expression that is after
is given by the expression that is after 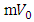 in Eq. (21), where
in Eq. (21), where 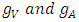 are the vector and axial vector coupling constants of the particles indicated by the subscripts with the Z-boson of the Standard model. The ratio
are the vector and axial vector coupling constants of the particles indicated by the subscripts with the Z-boson of the Standard model. The ratio 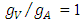 for all the neutrinos and it is introduced for future generalization. On the other hand,
for all the neutrinos and it is introduced for future generalization. On the other hand,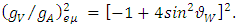 | (22) |
Where 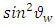 is the Weinberg mixing parameter. Eq.(21) is approximately
is the Weinberg mixing parameter. Eq.(21) is approximately 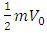 irrespective of the value of the mixing parameter. The mass of the electron neutrino is therefore,
irrespective of the value of the mixing parameter. The mass of the electron neutrino is therefore, 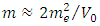 = 2.12eV. We took 0.5 for
= 2.12eV. We took 0.5 for 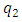 in Eq. (19) assuming a possibility that
in Eq. (19) assuming a possibility that 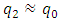 .Exact mass of the electron neutrino is, (with
.Exact mass of the electron neutrino is, (with 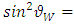
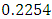 ),
),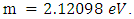 | (23) |
The above value appears correct. In Eq. (10) also the very last factor involving the constants 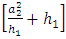 must as well be a function of gauge constants and from Ref. [5], it can be noted that,
must as well be a function of gauge constants and from Ref. [5], it can be noted that,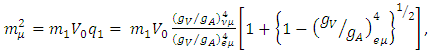 | (24) |
From the above the muon neutrino mass 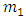 is given by,
is given by,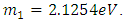 | (25) |
While computing the mass of the Tau-neutrino, we used the possibility in Eq. (20), that 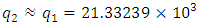 , which is
, which is 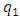 is from Eq. (24). The electron-neutrino and the muon -neutrino masses are nearly equal.Because of this the electron and muon mass ratio is given by,
is from Eq. (24). The electron-neutrino and the muon -neutrino masses are nearly equal.Because of this the electron and muon mass ratio is given by,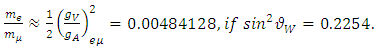 | (26) |
If 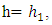 On the other hand, both these neutrinos will have the same mass. This mass can be arranged to be a Majorana mass, and these two Neutrinos together are equivalent to a single Dirac neutrino with the same mass, Ref. [5],
On the other hand, both these neutrinos will have the same mass. This mass can be arranged to be a Majorana mass, and these two Neutrinos together are equivalent to a single Dirac neutrino with the same mass, Ref. [5], | (27) |
With this there is no necessity of any right handed component for these Neutrinos. But then the electron and muon are subject to an electroweak Model, SU(2)LxSU(2)RXU(1) guage model with the mixing parameters 0.2254 and 0.2746. Identical mass for these two neutrinos is not supported by the observed neutrino oscillation. Hence the electron and Muon neutrinos have different masses and these are given by Eqs. (23) and (25).In place of 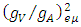 we take
we take 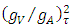 in both Eqs. (21) & (24) and find that, Ref. [6],
in both Eqs. (21) & (24) and find that, Ref. [6],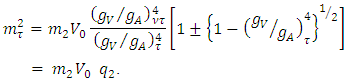 | (28) |
In Eq.(28), the expression after 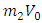 is similar to Eq.(24) with the plus Sign and with Eq.(21) with the negative sign.
is similar to Eq.(24) with the plus Sign and with Eq.(21) with the negative sign.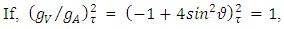 | (29) |
the expression after 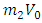 in the middle is just one and so
in the middle is just one and so 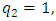 that means that the mixing parameter for the electroweak model of the tau lepton is 0.5. It is SU(2)LXU(1) gauge model with a different mixing parameter. The
that means that the mixing parameter for the electroweak model of the tau lepton is 0.5. It is SU(2)LXU(1) gauge model with a different mixing parameter. The 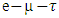 universality is no longer valid. Thus, the experimental determination of Tau-neutrino mass is very crucial [7,8,9]
universality is no longer valid. Thus, the experimental determination of Tau-neutrino mass is very crucial [7,8,9] 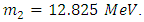 | (30) |
There is no evidence as of now for the non-universality of 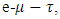 and Hence the mass of tau-neutrino may not be given by Eq.(30). But Eq.(27) may well be recast for the mass of the Tau neutrino,
and Hence the mass of tau-neutrino may not be given by Eq.(30). But Eq.(27) may well be recast for the mass of the Tau neutrino,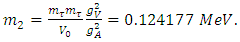 | (31) |
Where we replaced  by
by  assuming some sort of generality. We believe that the mass of the Tau neutrino is given by Eq.(31). While Estimating the above value the Weinberg mixing parameter is taken to Be 0.2254. If we take it to be 0.23 these numbers will be substantially quite different. In order to obtain Eq.(31), we note that Eq.(28) must be,
assuming some sort of generality. We believe that the mass of the Tau neutrino is given by Eq.(31). While Estimating the above value the Weinberg mixing parameter is taken to Be 0.2254. If we take it to be 0.23 these numbers will be substantially quite different. In order to obtain Eq.(31), we note that Eq.(28) must be,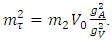 | (32) |
Experiments suggest that the theoretical estimations here of all the neutrino masses are right. The assumption that the neutrino mass eigen state exists and obtains its mass through its interaction with the same Higgs field through which the corresponding charged lepton obtains its mass is a departure from the Standard Model. But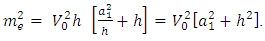 | (33) |
In which we shifted the neutrino mass constant. Suppose 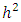 is very small compared to
is very small compared to 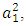 then we can assume that the neutrino has no interaction at all and our neutrino is massless and left-handed, but the electron mass is given by its interaction with the Higgs field. In a similar way the muon mass can be arranged and the muon neutrino has no mass apparently and it is left-handed like the electron neutrino. Note that the constant h is about 8.6x 10-12, from the electron neutrino mass. The square of this constant is definitely very small compared to the other number in Eq. (33)
then we can assume that the neutrino has no interaction at all and our neutrino is massless and left-handed, but the electron mass is given by its interaction with the Higgs field. In a similar way the muon mass can be arranged and the muon neutrino has no mass apparently and it is left-handed like the electron neutrino. Note that the constant h is about 8.6x 10-12, from the electron neutrino mass. The square of this constant is definitely very small compared to the other number in Eq. (33)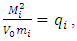 | (34) |
where 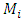 is the mass of the corresponding charged lepton and
is the mass of the corresponding charged lepton and 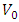 is the VEV which is known. From
is the VEV which is known. From 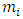 the parameter h can be found and then the corresponding
the parameter h can be found and then the corresponding 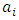 can as well be calculated and it fixes the CP transformation.
can as well be calculated and it fixes the CP transformation.
3. Two State Mixing of Neutrinos
As in the case of quarks the lepton mass matrix may not be diagonal.It will lead to a mixed state of the two neutrinos much like Cabibbo Mixing of quarks. For obtaining the electron-neutrino & muon-neutrino Mixing we proceed in the following, Ref. [10,11], way.Let the electron and its neutrino mass matrix be given by, 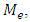 where,
where, 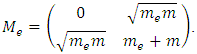 | (35) |
This mass matrix is diagonalized by an orthogonal matrix, 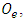 where,
where,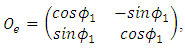 | (36) |
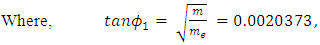 | (37) |
From the above we note that,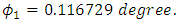 | (38) |
Let the mass matrix for the muon and its neutrino be given by the matrix, 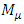 where,
where,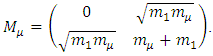 | (39) |
The above mass matrix is diagonalized by an orthogonal matrix 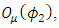
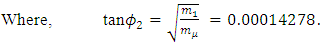 | (40) |
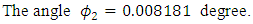 | (41) |
The absolute mass eigen-states 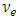 of the electron- neutrino and the absolute mass eigen state
of the electron- neutrino and the absolute mass eigen state 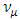 of the muon-neutrino are not the eigen States that take part in the electroweak model. Instead they mix and appear as a mixed states much like the Cabibbo-mixed states.
of the muon-neutrino are not the eigen States that take part in the electroweak model. Instead they mix and appear as a mixed states much like the Cabibbo-mixed states.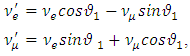 | (42) |
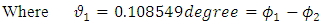 | (43) |
This is much like the Cabibbo mixing in the quark sector. To obtain this mixing angle we used the non-diagonal mass matrices, 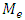 and
and 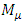 . [10]. In view of the mixing of
. [10]. In view of the mixing of 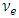 and
and 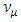 with the mixing angle
with the mixing angle 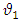 the relative Phase of
the relative Phase of 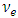 and
and 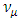 changes because of the mass difference so that a neutrino originating as
changes because of the mass difference so that a neutrino originating as 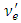 has a non-zero probability of being detected as
has a non-zero probability of being detected as 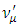 . If an electron-type of neutrino is propagating with momentum
. If an electron-type of neutrino is propagating with momentum 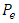 at time t=0, it will have a probability of oscillation
at time t=0, it will have a probability of oscillation 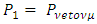 , where,
, where, 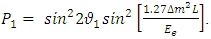 | (44) |
Here, 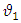 is given by Eq. (43), and,
is given by Eq. (43), and,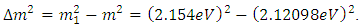 | (45) |
Moreover 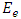 is the initial energy of the electron- neutrino in GeV and L is in km. Ref. [9].
is the initial energy of the electron- neutrino in GeV and L is in km. Ref. [9].
4. Electron and Tau Neutrino Mixing
We follow an exact mass mixing procedure to obtain the electron and Tau-neutrino mixing, again we assume two flavor mixing. In order to find the mixing angle of the Tau-neutrino with the electron-neutrino, we consider the following mass matrix for the Tau and its neutrino again assuming as though there are two generations.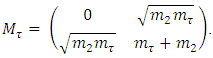 | (46) |
This matrix is diagonalized by the orthogonal matrix 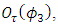 where
where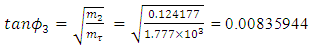 | (47) |
From the above, the angle 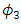 is given by,
is given by,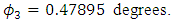 | (48) |
The electron-neutrino and the Tau-neutrino mix where the mixing angle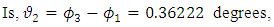 | (49) |
The mixed neutrino states are given by,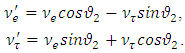 | (50) |
Because of this mixing, a neutrino 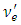 which starts with energy
which starts with energy 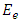 will Oscillate into a neutrino
will Oscillate into a neutrino 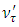 with a probability,
with a probability, 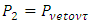 given by
given by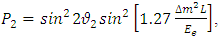 | (51) |
Where 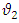 is given by Eq.(49), and, [see Ref. [9]].
is given by Eq.(49), and, [see Ref. [9]].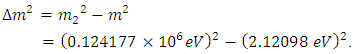 | (52) |
5. Muon-Tau Neutrino Mixing
The muon neutrino can also mix with the tau neutrino exactly like the electron neutrino. The Cabibbo type of mixing angle in this case is given by, 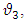 where,
where,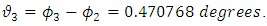 | (53) |
The mixed neutrino states are given by,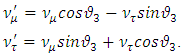 | (54) |
Because of the above mixing a 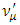 neutrino with initial Energy
neutrino with initial Energy 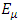 oscillates into a
oscillates into a 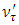 with a probability,
with a probability,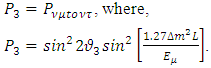 | (55) |
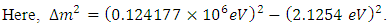 | (56) |
6. Conclusions
From the mass matrices we obtained the necessary theoretical data to Verify the flavor violation. Instead of two flavor mixing we should consider three by three mass mixings. But the present analysis should Yield at least approximate results. The masses of the neutrinos will be Slightly different if we take the Weinberg mixing parameter = 0.23.
References
| [1] | Particle Data Group, Progress of Theort. Phys, 083c1 (2020). |
| [2] | Weinberg. S Phys. Rev. Letts. 19, 1264, (1967). |
| [3] | Mohapatra R.N. Sanjanovic G, Phys. Rev. Letts. 44, 912 (1980). |
| [4] | Bilenkey S.M, Petrov S.T Rev. Mod. Phys 59,671 (1987). |
| [5] | Raju. Cvavbc Intl. Jour. Theort. Phys Vol. 36, No. 12 2937 (1997). |
| [6] | Raju. Cvavbc Turk. Jour. Phys. Vol. 32, 59, (2008). |
| [7] | Gonzalez M.C-Garcia, Neutrino Masses & Mixing. YITP Aug (2019) Stony Brook. |
| [8] | Drexlin, et all, Adv. In High Energy Phys. Vol. 2013, article Id 293986. |
| [9] | Barry C Barish, Tau Neutrino PHYS, An Introduction, Cal. Teh. lecture. |
| [10] | H. Fritzsch, phys. Rev. Lett, B 155(1979), 189. |
| [11] | L. F. Li, phys. Rev. Lett. B84, (1979), 461. |



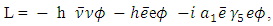
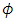 with the VEV
with the VEV 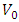 , and h in Eq. (1), is very small and we are not assuming that the neutrino is left-handed. It is a full mass eigenstate. The electron is coupled to the Higgs field through a
, and h in Eq. (1), is very small and we are not assuming that the neutrino is left-handed. It is a full mass eigenstate. The electron is coupled to the Higgs field through a 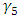 coupling also. We recover the standard model scenario when h is set zero and i
coupling also. We recover the standard model scenario when h is set zero and i 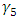 is replaced by one. Given a Dirac field say,
is replaced by one. Given a Dirac field say, 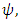 the Hermitian Scalar
the Hermitian Scalar 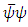 and
and 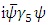 have opposite CP and T transformation properties (In this respect they are unlike the vector and axial vector.) The CP violation is now caused by the exchange of
have opposite CP and T transformation properties (In this respect they are unlike the vector and axial vector.) The CP violation is now caused by the exchange of 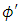 fields. Since the coupling of Higgs Field is usually rather small, it is possible to arrange for the CP violation to be of roughly milliweak magnitude [Mohapatra 1980, Bilenkey, 3&4].After spontaneous symmetry breaking from (1) we note that,
fields. Since the coupling of Higgs Field is usually rather small, it is possible to arrange for the CP violation to be of roughly milliweak magnitude [Mohapatra 1980, Bilenkey, 3&4].After spontaneous symmetry breaking from (1) we note that,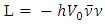
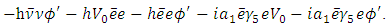 And with,
And with, 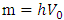 , which is now the electron-neutrino mass,
, which is now the electron-neutrino mass, 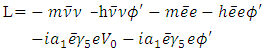
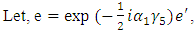
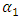 is a real parameter. Vector and axial vector interactions are not affected by this transformation. We choose
is a real parameter. Vector and axial vector interactions are not affected by this transformation. We choose 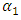 in such a way that the constant coefficient of
in such a way that the constant coefficient of 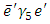 is zero. This gives,
is zero. This gives,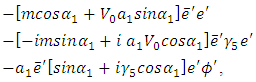
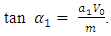
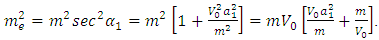
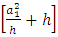 , which are the interaction constants of the Higgs field with the electron and its neutrino, [Eq.(2)]. Let,
, which are the interaction constants of the Higgs field with the electron and its neutrino, [Eq.(2)]. Let,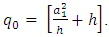
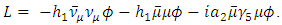
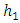 and
and 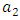 are real positive numbers and after symmetry breaking, the muon neutrino obtains the following mass:
are real positive numbers and after symmetry breaking, the muon neutrino obtains the following mass: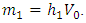
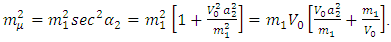
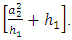 Let,
Let,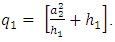
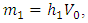 and with the same VEV,
and with the same VEV,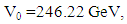
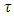 lepton. Its mass is,
lepton. Its mass is,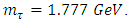
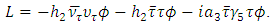
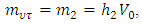
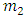 is the mass of the
is the mass of the 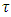 -neutrino and the mass of the charged
-neutrino and the mass of the charged 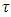 lepton is now given by,
lepton is now given by,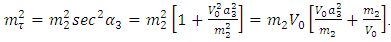
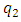 where,
where, 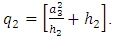
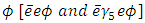 in two ways, and this sort of coupling is also there with the standard Z-boson. Using this clue, we tried to relate the masses of the electron and muon to the interaction constants
in two ways, and this sort of coupling is also there with the standard Z-boson. Using this clue, we tried to relate the masses of the electron and muon to the interaction constants 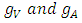 of the Z boson in Ref. [5].First let us note how a simple choice of
of the Z boson in Ref. [5].First let us note how a simple choice of 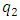 enables the prediction of Tau -neutrino mass.
enables the prediction of Tau -neutrino mass.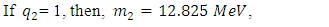
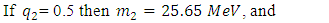
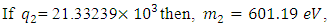
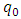 is chosen as a function of gauge constants [5].
is chosen as a function of gauge constants [5].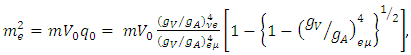
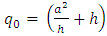 is given by the expression that is after
is given by the expression that is after 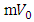 in Eq. (21), where
in Eq. (21), where 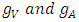 are the vector and axial vector coupling constants of the particles indicated by the subscripts with the Z-boson of the Standard model. The ratio
are the vector and axial vector coupling constants of the particles indicated by the subscripts with the Z-boson of the Standard model. The ratio 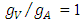 for all the neutrinos and it is introduced for future generalization. On the other hand,
for all the neutrinos and it is introduced for future generalization. On the other hand,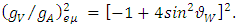
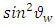 is the Weinberg mixing parameter. Eq.(21) is approximately
is the Weinberg mixing parameter. Eq.(21) is approximately 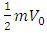 irrespective of the value of the mixing parameter. The mass of the electron neutrino is therefore,
irrespective of the value of the mixing parameter. The mass of the electron neutrino is therefore, 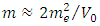 = 2.12eV. We took 0.5 for
= 2.12eV. We took 0.5 for 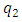 in Eq. (19) assuming a possibility that
in Eq. (19) assuming a possibility that 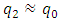 .Exact mass of the electron neutrino is, (with
.Exact mass of the electron neutrino is, (with 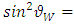
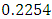 ),
),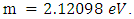
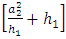 must as well be a function of gauge constants and from Ref. [5], it can be noted that,
must as well be a function of gauge constants and from Ref. [5], it can be noted that,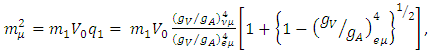
 is given by,
is given by,
 , which is
, which is 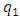 is from Eq. (24). The electron-neutrino and the muon -neutrino masses are nearly equal.Because of this the electron and muon mass ratio is given by,
is from Eq. (24). The electron-neutrino and the muon -neutrino masses are nearly equal.Because of this the electron and muon mass ratio is given by,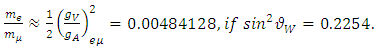
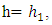 On the other hand, both these neutrinos will have the same mass. This mass can be arranged to be a Majorana mass, and these two Neutrinos together are equivalent to a single Dirac neutrino with the same mass, Ref. [5],
On the other hand, both these neutrinos will have the same mass. This mass can be arranged to be a Majorana mass, and these two Neutrinos together are equivalent to a single Dirac neutrino with the same mass, Ref. [5],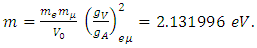
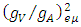 we take
we take 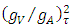 in both Eqs. (21) & (24) and find that, Ref. [6],
in both Eqs. (21) & (24) and find that, Ref. [6],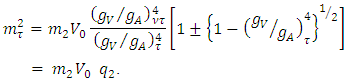
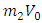 is similar to Eq.(24) with the plus Sign and with Eq.(21) with the negative sign.
is similar to Eq.(24) with the plus Sign and with Eq.(21) with the negative sign.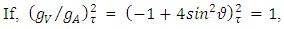
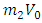 in the middle is just one and so
in the middle is just one and so 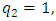 that means that the mixing parameter for the electroweak model of the tau lepton is 0.5. It is SU(2)LXU(1) gauge model with a different mixing parameter. The
that means that the mixing parameter for the electroweak model of the tau lepton is 0.5. It is SU(2)LXU(1) gauge model with a different mixing parameter. The 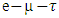 universality is no longer valid. Thus, the experimental determination of Tau-neutrino mass is very crucial [7,8,9]
universality is no longer valid. Thus, the experimental determination of Tau-neutrino mass is very crucial [7,8,9] 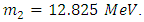
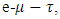 and Hence the mass of tau-neutrino may not be given by Eq.(30). But Eq.(27) may well be recast for the mass of the Tau neutrino,
and Hence the mass of tau-neutrino may not be given by Eq.(30). But Eq.(27) may well be recast for the mass of the Tau neutrino,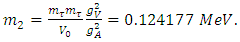
 by
by 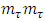 assuming some sort of generality. We believe that the mass of the Tau neutrino is given by Eq.(31). While Estimating the above value the Weinberg mixing parameter is taken to Be 0.2254. If we take it to be 0.23 these numbers will be substantially quite different. In order to obtain Eq.(31), we note that Eq.(28) must be,
assuming some sort of generality. We believe that the mass of the Tau neutrino is given by Eq.(31). While Estimating the above value the Weinberg mixing parameter is taken to Be 0.2254. If we take it to be 0.23 these numbers will be substantially quite different. In order to obtain Eq.(31), we note that Eq.(28) must be,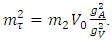
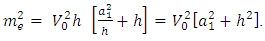
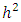 is very small compared to
is very small compared to 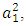 then we can assume that the neutrino has no interaction at all and our neutrino is massless and left-handed, but the electron mass is given by its interaction with the Higgs field. In a similar way the muon mass can be arranged and the muon neutrino has no mass apparently and it is left-handed like the electron neutrino. Note that the constant h is about 8.6x 10-12, from the electron neutrino mass. The square of this constant is definitely very small compared to the other number in Eq. (33)
then we can assume that the neutrino has no interaction at all and our neutrino is massless and left-handed, but the electron mass is given by its interaction with the Higgs field. In a similar way the muon mass can be arranged and the muon neutrino has no mass apparently and it is left-handed like the electron neutrino. Note that the constant h is about 8.6x 10-12, from the electron neutrino mass. The square of this constant is definitely very small compared to the other number in Eq. (33)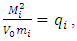
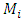 is the mass of the corresponding charged lepton and
is the mass of the corresponding charged lepton and 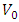 is the VEV which is known. From
is the VEV which is known. From 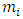 the parameter h can be found and then the corresponding
the parameter h can be found and then the corresponding 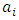 can as well be calculated and it fixes the CP transformation.
can as well be calculated and it fixes the CP transformation.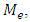 where,
where, 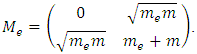
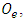 where,
where,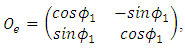
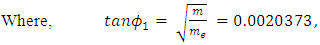
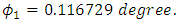
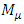 where,
where,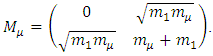
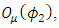
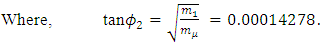
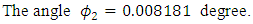
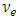 of the electron- neutrino and the absolute mass eigen state
of the electron- neutrino and the absolute mass eigen state 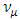 of the muon-neutrino are not the eigen States that take part in the electroweak model. Instead they mix and appear as a mixed states much like the Cabibbo-mixed states.
of the muon-neutrino are not the eigen States that take part in the electroweak model. Instead they mix and appear as a mixed states much like the Cabibbo-mixed states.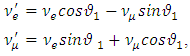
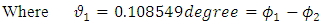
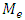 and
and 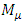 . [10]. In view of the mixing of
. [10]. In view of the mixing of 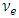 and
and 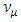 with the mixing angle
with the mixing angle 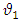 the relative Phase of
the relative Phase of 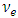 and
and 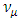 changes because of the mass difference so that a neutrino originating as
changes because of the mass difference so that a neutrino originating as 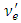 has a non-zero probability of being detected as
has a non-zero probability of being detected as 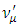 . If an electron-type of neutrino is propagating with momentum
. If an electron-type of neutrino is propagating with momentum 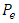 at time t=0, it will have a probability of oscillation
at time t=0, it will have a probability of oscillation 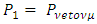 , where,
, where, 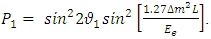
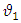 is given by Eq. (43), and,
is given by Eq. (43), and,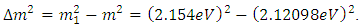
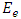 is the initial energy of the electron- neutrino in GeV and L is in km. Ref. [9].
is the initial energy of the electron- neutrino in GeV and L is in km. Ref. [9].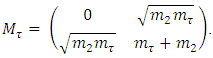
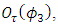 where
where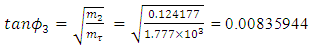
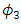 is given by,
is given by,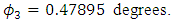
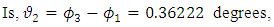
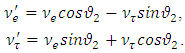
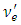 which starts with energy
which starts with energy 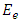 will Oscillate into a neutrino
will Oscillate into a neutrino 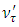 with a probability,
with a probability, 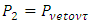 given by
given by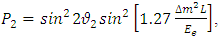
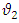 is given by Eq.(49), and, [see Ref. [9]].
is given by Eq.(49), and, [see Ref. [9]].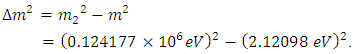
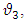 where,
where,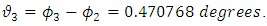
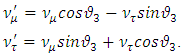
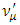 neutrino with initial Energy
neutrino with initial Energy 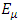 oscillates into a
oscillates into a 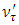 with a probability,
with a probability,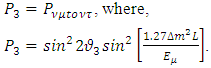
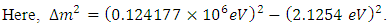
 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML