-
Paper Information
- Paper Submission
-
Journal Information
- About This Journal
- Editorial Board
- Current Issue
- Archive
- Author Guidelines
- Contact Us
Journal of Nuclear and Particle Physics
p-ISSN: 2167-6895 e-ISSN: 2167-6909
2021; 11(2): 38-46
doi:10.5923/j.jnpp.20211102.02
Received: Aug. 3, 2021; Accepted: Aug. 18, 2021; Published: Aug. 25, 2021

Single-particle Properties of Asymmetric Nuclear Matter Based on Two- and Three-Body Forces within Brueckner Theory
Khaled S. A. Hassaneen, Alaa M. El-Sheikh, Hoda M. Abou-Elsebaa
Physics Department, Faculty of Science, Sohag University, Sohag, Egypt
Correspondence to: Khaled S. A. Hassaneen, Physics Department, Faculty of Science, Sohag University, Sohag, Egypt.
| Email: |  |
Copyright © 2021 The Author(s). Published by Scientific & Academic Publishing.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/

We study the single-particle (sp) properties of asymmetric nuclear within the framework of the Brueckner-Hartree-Fock (BHF) approach extended by including a phenomenological three-body force (3BF). These properties are the single-particle energy, the nucleon effective masses and the nuclear symmetry potential. Two kinds of realistic nucleon-nucleon interactions have been extensively used in the present BHF calculations. One is the charge-dependent Bonn potential (CD-Bonn) and the other is local soft core Argonne (V18). It is demonstrated that the single-particle potential becomes more attractive for the proton and more repulsive for the neutron at higher asymmetries. Also, the symmetry potentials at the normal density for different asymmetry parameters are in good agreement with the empirical value constrained by the experimental data. Finally, the neutron and proton effective masses show strong isospin splitting with m*n > m*p on the whole range of asymmetry parameters. So the 3BF force has effects turn out to be crucial for predicting reliably the sp properties within the Brueckner framework.
Keywords: Asymmetric Nuclear Matter, Single-Particle Potential, Effective mass, Nuclear Symmetry Potential
Cite this paper: Khaled S. A. Hassaneen, Alaa M. El-Sheikh, Hoda M. Abou-Elsebaa, Single-particle Properties of Asymmetric Nuclear Matter Based on Two- and Three-Body Forces within Brueckner Theory, Journal of Nuclear and Particle Physics, Vol. 11 No. 2, 2021, pp. 38-46. doi: 10.5923/j.jnpp.20211102.02.
Article Outline
1. Introduction
- One of the fundamental points of nuclear physics and nuclear astrophysics is to study the single particle (sp) properties of asymmetric nuclear matter in a wide range of density. The momentum dependence of the single-particle (sp) potential in nuclear medium is described by nucleon effective mass. The nucleon effective masses assumes a significant part in understanding many intriguing physical quantities in nuclear physics and astrophysics [1], like the properties of nucleon superfluidity in nuclear matter [2], nucleon-nucleon (NN) cross sections in thick nuclear matter [3] and the dynamical advancement of heavy-ion collisions (HIC) at intermediate energies [4].The determination of the momentum-dependence of symmetry potential and the neutron-proton effective mass splitting in neutron-rich nuclear matter is receiving more and more attention [5]. These properties are depend on the structure of asymmetric nuclear matter at densities around and below the nuclear saturation density. The properties of asymmetric nuclear matter can be anticipated by embracing different nuclear many-body approaches, including phenomenological methods and microscopic approaches.It is well known that the non-relativistic approaches using realistic two-body NN interactions are not reproduce the correct saturation point of symmetric nuclear matter, and three-body forces (3BF) are required [6]. In recent years, the sp properties of asymmetric nuclear matter have been investigated extensively within the framework of various microscopic approaches including the Brueckner-Hartree-Fock (BHF), and the extended BHF approaches [7,8], the relativistic Dirac-BHF (DBHF) theory [9], the in-medium T-matrix and Green function methods [10], and the many- body variational approach [11]. There are two kinds of 3BF, the phenomenological 3BF such as the Urbana 3BF [12] and the microscopic one [13].The paper is arranged as follows. In the next section we discuss the BHF approach of asymmetric nuclear matter, then we extend it to include the 3BF rearrangement contribution in calculating sp properties in asymmetric nuclear matter. Our numerical results are reported in Sec. III, we will concentrate on the discussion of the effects of the 3BF rearrangement on neutron and proton sp properties including the sp potentials, the isospin splitting of the effective mass and the density dependence of the symmetry potential, based on the BHF approximation and BHF with the inclusion of phenomenological 3BF using two realistic nucleon-nucleon potentials are the CD-Bonn potential and Argonne (V18) potential. Finally, we summarize our present investigation in Sec. IV.
2. The BHF Approach of Asymmetric Matter
- The BHF approach of asymmetric nuclear matter [14-18] starts with the construction of all the G matrices describing the effective interaction between two nucleons in the presence of a surrounding medium. They are obtained by solving the well-known Bethe-Goldstone equation
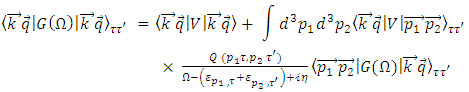 | (1) |
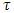 = n,p indicates the isospin projection of the two nucleons in the initial, intermediate and final states, V denotes the bare NN interaction,
= n,p indicates the isospin projection of the two nucleons in the initial, intermediate and final states, V denotes the bare NN interaction, 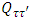 the Pauli operator that allows only intermediate states compatible with the Pauli principle, and ω, the so-called starting energy, corresponds to the sum of non-relativistic energies of the interacting nucleons. The single-particle energy
the Pauli operator that allows only intermediate states compatible with the Pauli principle, and ω, the so-called starting energy, corresponds to the sum of non-relativistic energies of the interacting nucleons. The single-particle energy 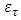 of a nucleon with momentum
of a nucleon with momentum 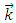 is given by
is given by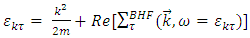 | (2) |
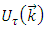 or self-energy of a nucleon with isospin
or self-energy of a nucleon with isospin 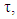 represents the mean field "felt" by a nucleon due to its interaction with the other nucleons of the medium. In the BHF approach,
represents the mean field "felt" by a nucleon due to its interaction with the other nucleons of the medium. In the BHF approach, 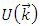 is calculated through the "on-shell energy" G-matrix, and is given by
is calculated through the "on-shell energy" G-matrix, and is given by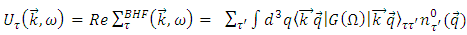 | (3) |
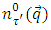 refers to the occupation probability of a free Fermi gas of protons
refers to the occupation probability of a free Fermi gas of protons 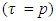 and neutrons
and neutrons 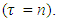 This means for asymmetric matter with a total density ρ and asymmetry α
This means for asymmetric matter with a total density ρ and asymmetry α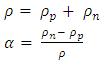 | (4) |
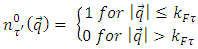 | (5) |
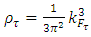 | (6) |
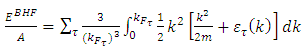 | (7) |
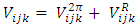 | (8) |
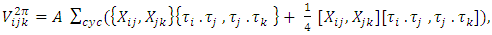 | (9) |
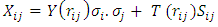 | (10) |
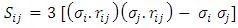 is the tensor operator. Y(r) and T(r) are the Yukawa and tensor functions, respectively, associated to the one- pion exchange, as in the two {body potential. The repulsive part is taken as
is the tensor operator. Y(r) and T(r) are the Yukawa and tensor functions, respectively, associated to the one- pion exchange, as in the two {body potential. The repulsive part is taken as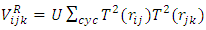 | (11) |
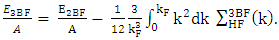 | (12) |
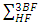 coming from the 3BF is calculated from an effective two nucleons potential at the lowest order, in keeping with the procedure established Ref. [22].Regarding Un/p as functions of the asymmetry parameter α, one can easily verify that the following approximate relation applies [26]
coming from the 3BF is calculated from an effective two nucleons potential at the lowest order, in keeping with the procedure established Ref. [22].Regarding Un/p as functions of the asymmetry parameter α, one can easily verify that the following approximate relation applies [26]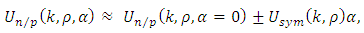 | (13) |
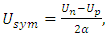 | (14) |
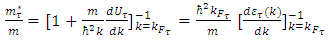 | (15) |
3. Results and Discussion
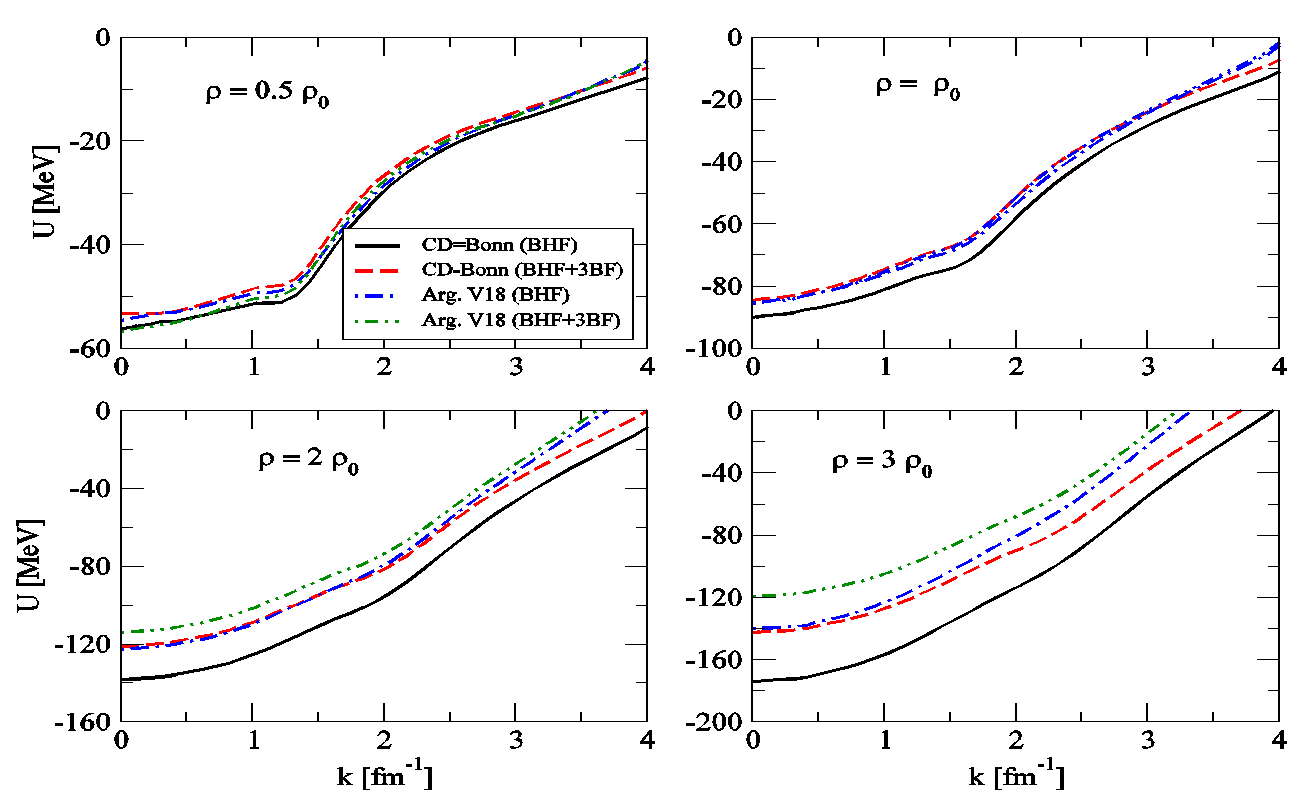
- As a first step we would like to discuss the single-particle potentials or the real part of self-energies as a function of the asymmetry parameter of nuclear matter α. For that purpose we consider nuclear matter at the empirical value for the saturation density of symmetric nuclear matter (ρ = 0.16 fm-3) and consider the self-energies for various values of the asymmetry parameter α. All the results discussed in this work have been computed for the charge-dependent Bonn (CD-Bonn) potential, defined in [27], which is nonlocal and exhibits a softer tensor component compared to another realistic nucleon-nucleon potential such as the Argonne V18 [28], which are local. As well, it represents a phenomenological parameterization in real space, including 18 spin-isospin operators. It is a typical example of a particularly strong, but finite, short-range core.In order to discuss clearly the 3BF effects, firstly, we compare in Figure 1. the single-particle potentials or real-part of the on-shell self-energies in symmetric nuclear matter for both approaches obtained in four different densities ranging from 0.08, 0.16, 0.32 to 0.48 fm-3. In the case of CD-Bonn interaction, it is seen that the single-particle potential at the BHF level (solid curves) without including any 3BF is most attractive. At low densities below and around the normal nuclear matter density, the 3BF effects (red dashed curves) are reasonably small.
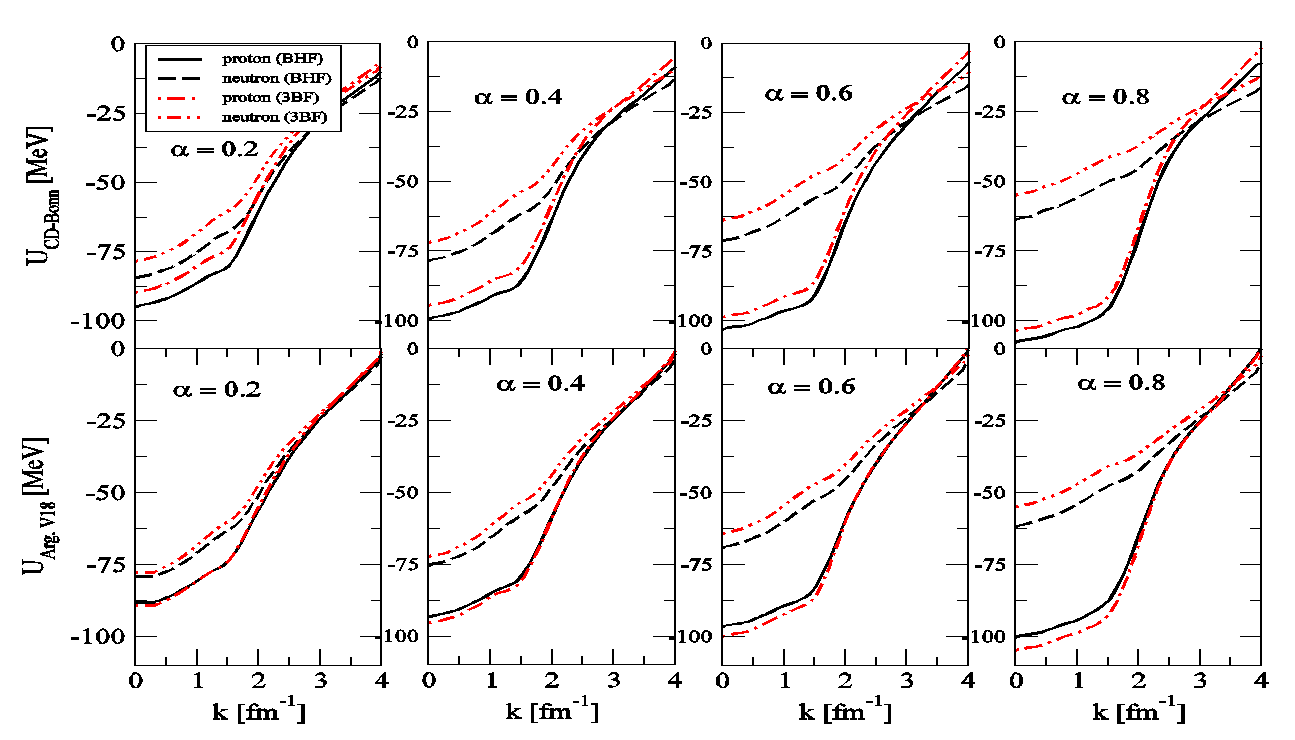
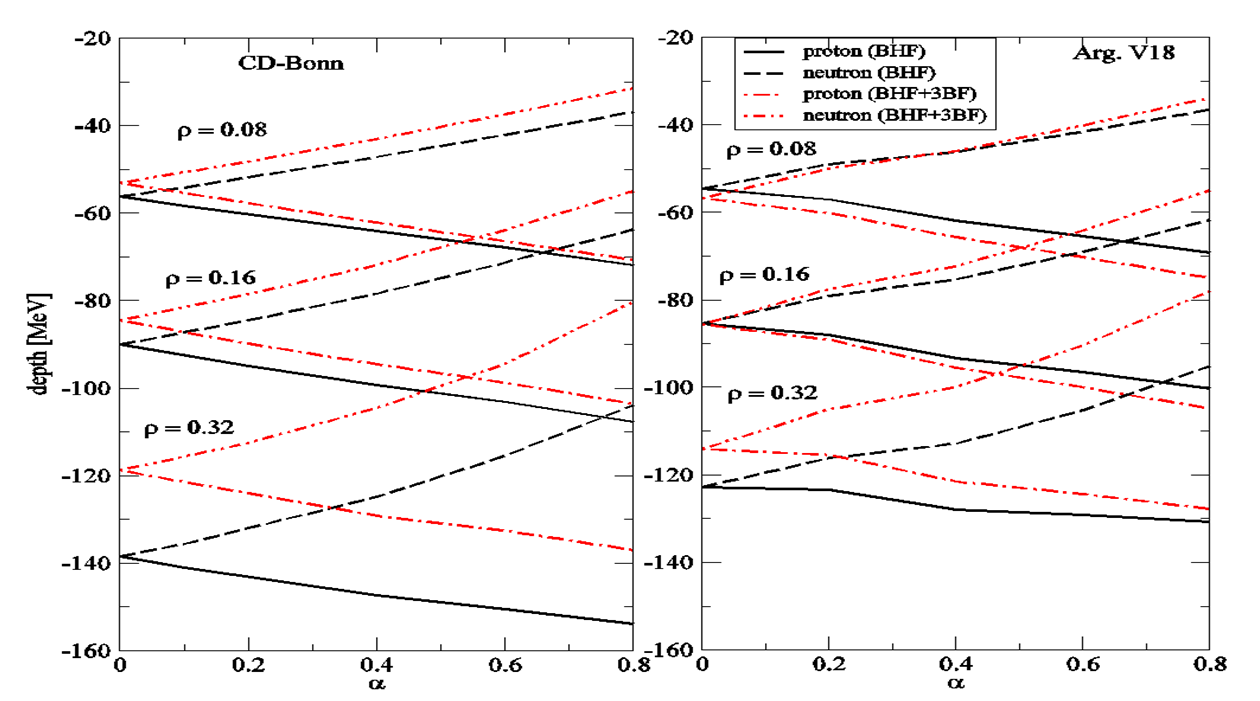 | Figure 3. The proton and neutron single-particle potentials as a function of the asymmetry parameter α at various densities and momentum equal to zero, i.e. potential depth |
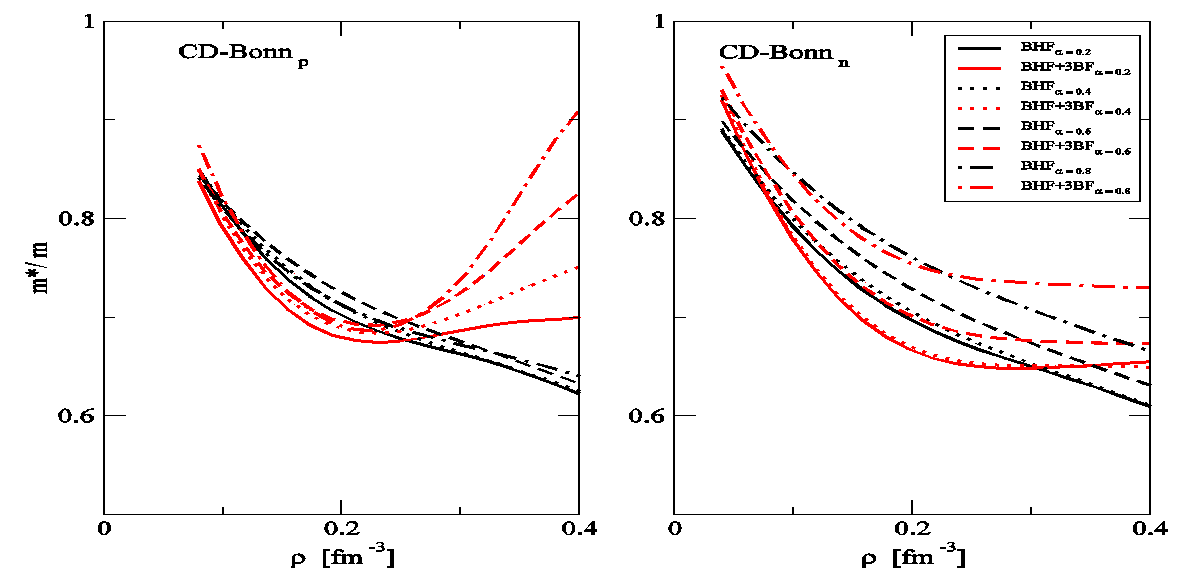
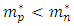 on the whole range of asymmetry parameters.
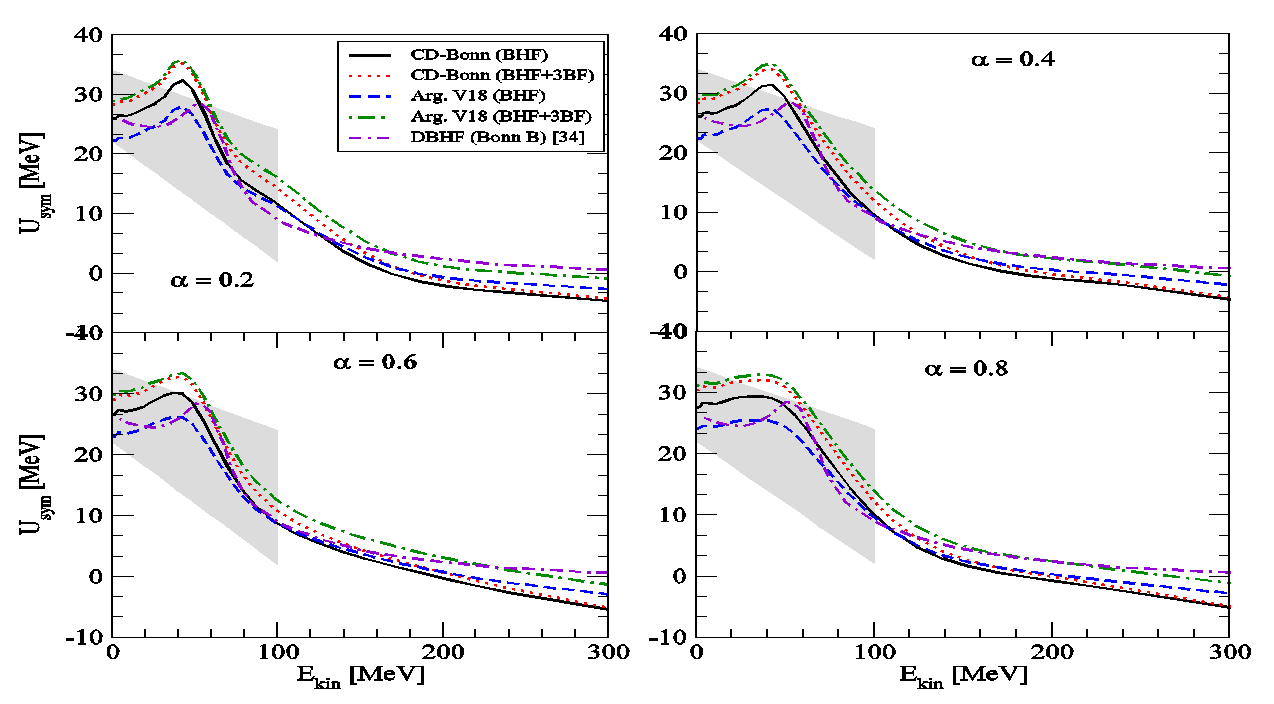
on the whole range of asymmetry parameters. 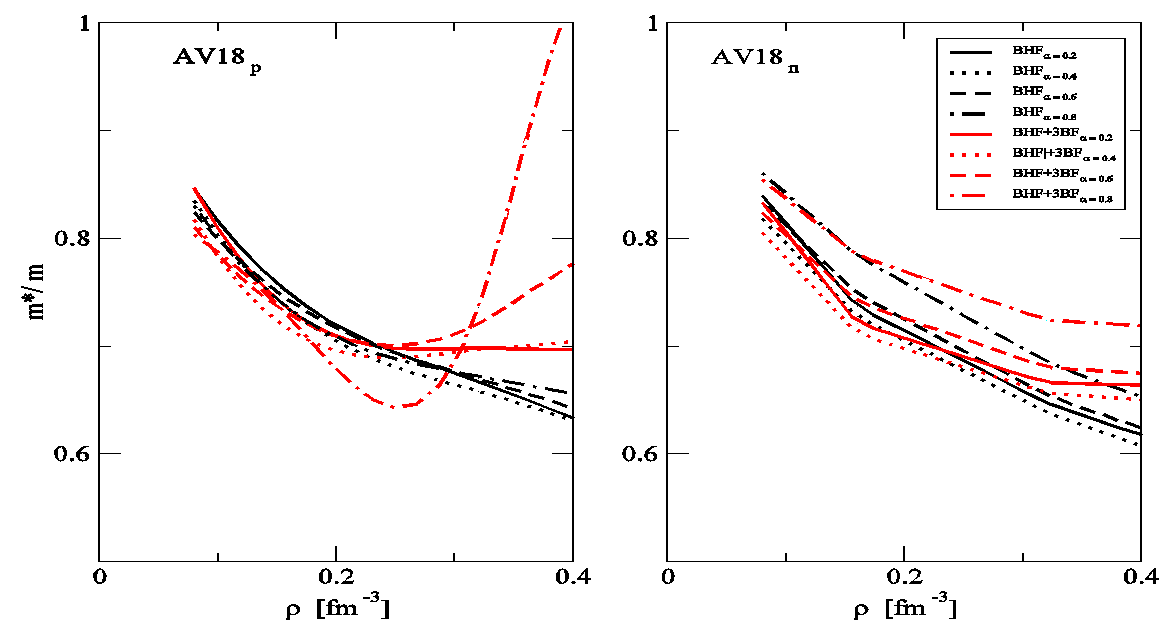 | Figure 7. The same as Figure 7. but using Argonne V18 potential |
4. Conclusions
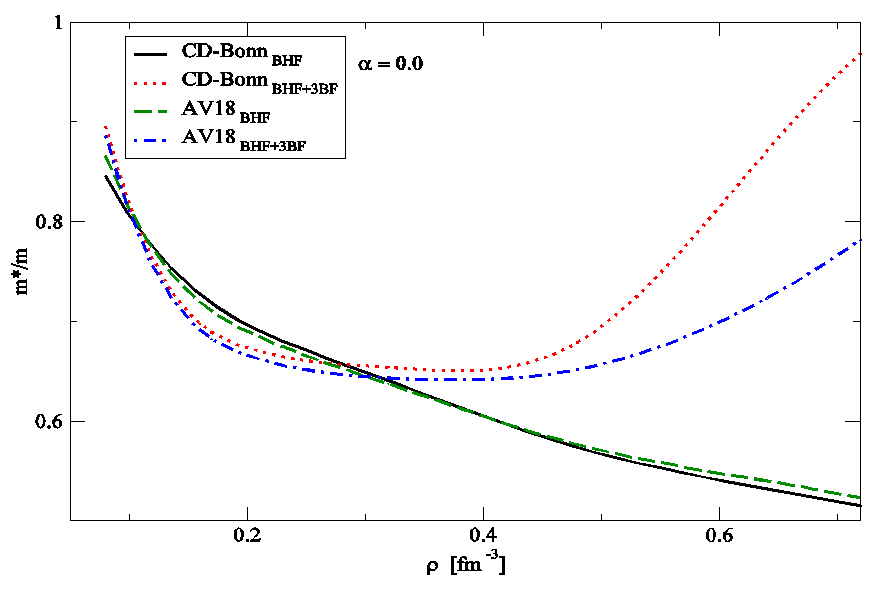
- The sp properties of asymmetric nuclear matter within the BHF approach with and without the inclusion of 3BF are studied. It is found that the 3BF make the results of the single-particle potential more repulsion than BHF only and the Argonne V18 potential is more repulsive than CD-Bonn potential. It is demonstrated that the single-particle potential becomes more attractive for the proton and more repulsive for the neutron at higher values of α. The isospin symmetry potentials at the normal density for different α is calculated, the results are in good agreement with the empirical information from Lane potential. We have predicted the nucleon effective masses and their isospin dependence in asymmetric nuclear matter, at low densities, the 3BF effect is fairly small. Also, the neutron and proton effective masses show strong isospin splitting with
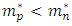 on the whole range of asymmetry parameters.
on the whole range of asymmetry parameters.ACKNOWLEDGEMENTS
- One of the authors, Khaled S. A. Hassaneen, would like to thank Professors H. Müther for helpful discussions and guidance as well as Professor M. Baldo for providing three-body force code.
 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML