-
Paper Information
- Paper Submission
-
Journal Information
- About This Journal
- Editorial Board
- Current Issue
- Archive
- Author Guidelines
- Contact Us
Journal of Nuclear and Particle Physics
p-ISSN: 2167-6895 e-ISSN: 2167-6909
2021; 11(2): 27-37
doi:10.5923/j.jnpp.20211102.01
Received: Mar. 1, 2021; Accepted: Mar. 22, 2021; Published: Apr. 25, 2021

Laws of Gravity and Electrostatics Reduce Elementary Particles to Only Two – Positron and Negatron
Misheck Kirimi
Moi University, Kesses, Eldoret, Kenya
Correspondence to: Misheck Kirimi, Moi University, Kesses, Eldoret, Kenya.
| Email: |  |
Copyright © 2021 The Author(s). Published by Scientific & Academic Publishing.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/

I demonstrate that the macrocosmic gravitational interaction between two masses and the microcosmic electrostatic interaction between two charges unify in simple concepts and mathematical laws when electric charge and ordinary mass are interpreted in reciprocal terms. No previous research has ever attempted to unify electric charge and ordinary mass. The difficulty has been the lack of an intelligible definition of charge. A three-point paradigm shift solves the problem, giving convincing evidence – for the first time – that positive electron (positron) and negative electron (negatron) are the ultimate elementary particles. That is, matter is pure positive and negative grains of electricity. Paradigm shift #1: Electron is a moving charge; a charge is a static electron – a case of one entity two identities. This implies that, contrary to popular view, ordinary matter contains equal numbers of positrons and negatron – observed in motion as electrons and at rest as charges. In motion, a positron-negatron pair obeys the laws of electrodynamics and annihilates; at rest, the pair obeys the laws of electrostatics and neutralizes. Paradigm shift #2: Electron mass and electrostatic field are either positive or negative. Thus, opposite masses and fields, rather than indefinable ‘charge’, give opposite electrons physical distinctiveness. Paradigm shift #3: Electric charge and ordinary mass interconvert. Positive charge (e+) and negative charge (e-) neutralize to neutral charge (2e0), which is nature’s quantum of ordinary mass. Conversely, a quantum of ordinary mass splits to opposite charges e.g., in frictional electrification. The insights systematize the search, identification and classification of the baryons, ending decades of confusion in the ‘elementary particle zoo’. A third stable nucleon, in the order of proton and neutron, is identified and named the nairotron.
Keywords: Electron, Electrostatics, Elementary particles, Fields, Gravity, Unification
Cite this paper: Misheck Kirimi, Laws of Gravity and Electrostatics Reduce Elementary Particles to Only Two – Positron and Negatron, Journal of Nuclear and Particle Physics, Vol. 11 No. 2, 2021, pp. 27-37. doi: 10.5923/j.jnpp.20211102.01.
Article Outline
1. Introduction
- Newton discovered that masses M1 and M2 stationed distance r apart attract each other with a force (F) that is directly proportional to the product of the masses (M1M2) and inversely proportional to the square of the distance (r-2). Rearranging his equation: Fr2/MIM2 = G. About a century later Coulomb discovered that quantities of charge Q1 and Q2 obey a similar law: Fr2/QIQ2 = K. The two equations have a common mathematical configuration. In addition, the numerators describe the same entity (Fr2). However, the products of masses (M1M2) and charges (Q1Q2) swop places. Consequently, constants G and K are different. These observations change the traditional focus on ‘two types of interaction’ to ‘two types of matter that interact differently’. Attempts to explain the similarities and differences between Newton’s and Coulomb’s laws started soon after Coulomb published his finding [1]. For over 230 years, however, unification of electric and gravitational phenomena, in general, has eluded “some of the greatest minds in science” [2] – including Faraday [3], Einstein [4] and Weyl [5]. The long and fruitless search may mean that the phenomena have no natural link; or that a paradigm shift is required to spot the link.
2. Recent Studies
- Fragmented evidence hints that electrostatics and gravitation1 are different manifestations of a common interaction. For example, Spears derives gravitation constant (G) using only electrostatic parameters and concludes that “gravity is almost certainly an electrostatic phenomenon” [6]. But his findings remain at the level of mathematical abstraction without giving physical meaning to the numerical relations. Similarly, Greulich demonstrates that “gravitation can be rewritten completely as electrostatics” as long as one assigns to matter (ordinary mass) “a very small gravitational charge density” [7]. Greulich treats ordinary mass as a composite of infinitesimal quanta of electric charge and finds that ‘electric charge density’ and ‘gravitational charge density’ amount to the same thing. However, he does not explain what ‘charge densities’ mean in physical sense and why gravitation is only attractive. Haug, in agreement with Greulich, observes that for Planck masses Newton’s formula of gravitation is mathematically exactly the same as Coulomb’s formula of electrostatics. His observation suggests that at the most basic level of material structure – “at the very bottom of the rabbit hole” [8] – electric charge and ordinary mass have a common fabric. In a related study Aspden infers that gravity is the mutual electrostatic action between “material particles that are uncharged” [9]. In effect, Aspden equates gravitational mass to ‘neutral electric charge’. Consistent with Aspden’s proposal, Assis demonstrates that units of electrically uncharged particles – which he calls “neutral dipoles” – attracting electrostatically result in gravitation. The notion of ‘neutral dipoles’ suggests particles that are electrically neutral and yet exhibit internal polarity. Assis concludes that “gravitation is the statistical residual force between groups of neutral dipoles” [10]. More explicitly, he states that “heavy bodies are composed of oppositely charged particles” [11]. Beyond his statistical argument Assis does not interpret “neutral dipoles” or “oppositely charged particles” in familiar terms.The studies cited above point at a common inference that ‘unification of electrostatics and gravitation’ is essentially the ‘unification of electric charge and ordinary mass’. The inference agrees with the fact that charge (Q1Q2) and mass (M1M2) are the sole variables that Coulomb’s and Newton’s laws do not share. In other words, electric charge and ordinary mass are separate physical entities with similar and dissimilar interactive features. The similar features make Coulomb’s and Newton’s laws analogous. The dissimilar features result in two differences. 1) Coulomb’s matter (electric charge) either attracts or repels but Newton’s matter (ordinary mass) only attracts. 2) Coulomb’s interaction is much stronger than Newton’s interaction. The numerical value of Coulomb’s constant over Newton’s constant (K/G) shows that Fr2 per interacting charges (Fr2/QIQ2) is 1.347 x 1020 times greater than Fr2 per interacting masses (Fr2/MIM2). Hence, correct unification of electrostatics and gravitation is only possible if the natural relation of electric charge to ordinary mass is known. No past study has ever recognized or exploited this fact. Consequently, no one has ever established a natural link between gravity and electricity [12].
3. Unification of Charge and Mass
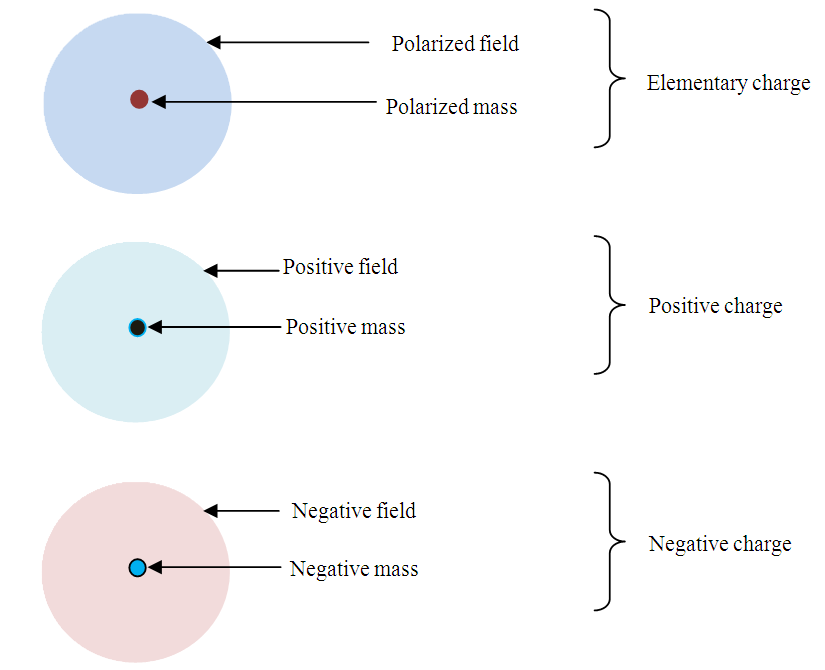
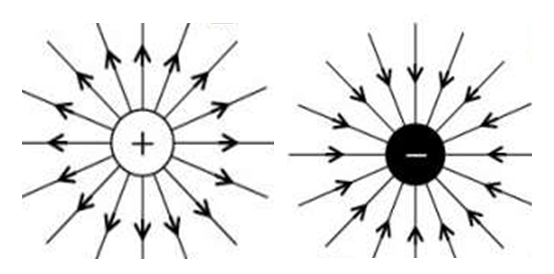
- Physics literature lacks any significant information on how nature relates electric charge to ordinary mass. The underlying difficulty has been the lack of clarity on the physical meaning of charge. Although charge has been recognized, analyzed and applied for centuries [13], its fundamental nature remains incoherent [14,15] – with no clear formulas linking it to better defined parameters [16]. This is a problem of great importance and “failure to solve it has restrained development in physics” [17]. Is charge so rudimentary that it has no further underlying meaning? Is it so unrelated to the rest of the physical realities that it cannot be interpreted in terms of anything else more comprehensible?There are scientific findings that explicitly define electric charge. It is known that charge is the sole material entity in electrostatic (Coulomb’s) interaction and ordinary mass is the sole material entity in gravitational (Newton’s) interaction. Therefore, the familiar entity that compares with electric charge is ordinary mass. Moreover, physicists have established two features that distinguish charge from ordinary mass. One, charge is quantized. Millikan proved “very directly” [18] that a quantity of charge is an aggregate of individual elementary charges. Similar quantization is not observed in ordinary mass. Two, charge is polarized2. This fact was first established by Dufay in 1733 [19]. In contrast, positive-negative symmetry is not observed in ordinary mass. Therefore, it can be inferred, without any scientific ambiguity, that charge is the ‘polarized type of matter’ and ordinary mass is the ‘unpolarized type of matter’. Polarized matter exhibits electric properties that include electrostatic interaction; unpolarized matter exhibits mechanical properties that include gravitational interaction. Hence, Coulomb’s law describes the interaction between quantities of polarized matter and Newton’s law gives a parallel account for unpolarized matter. The inference raises an imperative question: does nature polarize the unpolarized matter and vice versa? If this is shown to be the case, then electric charge and ordinary mass interconvert. Established scientific laws specify the aspects of a particle that are either polarized or unpolarized. For example, the law of gravitation resolves an unpolarized (gravitational) mass in two components: unpolarized inertial mass and unpolarized gravitational field (Fig. 1). Newton discovered that altering either the size or the position of a massive body produces instant mechanical effect in another massive body stationed across space. This entails instant transmission of mechanical energy between physical objects that have no obvious mechanical contact. The direct interpretation of this reality is that a gravitational mass is a single mechanical system comprising a tangible (inertial) mass and an intangible (gravitational) field. In Newton’s equation, the term MIM2 describes the contribution of inertial mass to gravitational force; and the term r-2 describes the contribution of gravitational field to the force. This interpretation, as demonstrated below, succeeds to explain a number of other observations. It means that gravitational field is no less a mechanical reality than inertial mass. The field is an invisible extension of gravitational mass beyond the edge of its tangible (inertial) mass. Whereas distance separates inertial masses, there is no distance between gravitational masses. In other words, two gravitational masses are mechanically connected all the time, such that even the slightest alteration in one is instantly reflected in the other. Hence, Newton’s Law of Universal Gravitation means that gravitational field mechanically connects every inertial mass to every other inertial mass. In this light, what seems like instant action at a distance [20] is instant action at no distance. Moreover, a mechanical field that originates in the center of mass and increases in direct proportion to the quantity of mass, and which extends and thins out equally in a three-dimension space, has the geometric properties that Einstein interpreted as curved space.For the first time, Maxwell’s vision of unified “field and substance” [21] is realized. In the case of gravitation, the “field” is the gravitational field and the “substance” is the inertial mass (Fig. 1). Firm theoretical and experimental evidence (presented shortly) shows that in the case of a polarized particle (a charge) the “field” is the electrostatic field and the “substance” is the electron mass (Fig. 2(a)). Put differently, the physical components of a charge are electron mass and electrostatic field. Unlike the components of a gravitational particle, the components of a charge are polarized – resulting in positive and negative charges (Fig. 2(b)). Hence, Coulomb’s and Newton’s laws relate the same variables – force, mass and field (distance). Differences arise because Coulomb deals with polarized mass and field and Newton deals with unpolarized mass and field.
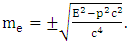 | (1) |
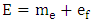 | (2) |
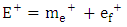 | (3) |
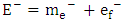 | (4) |
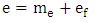 | (5) |
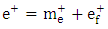 | (6) |
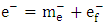 | (7) |
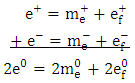 | (8) |
4. Predictions
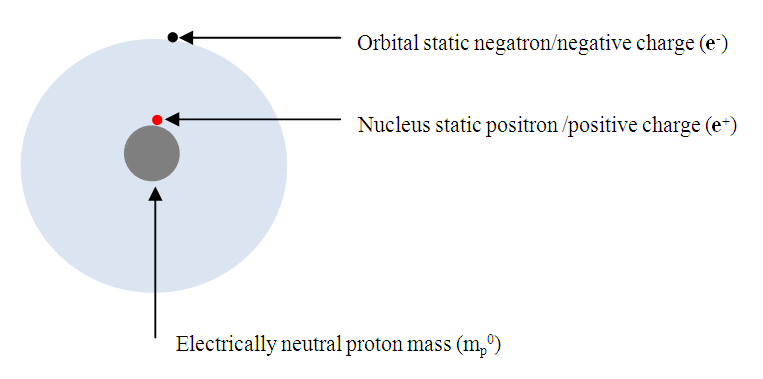
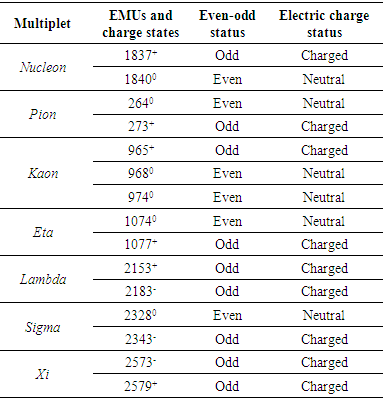
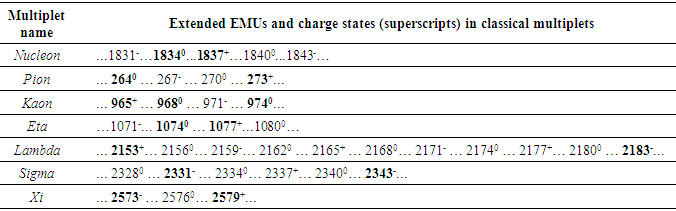
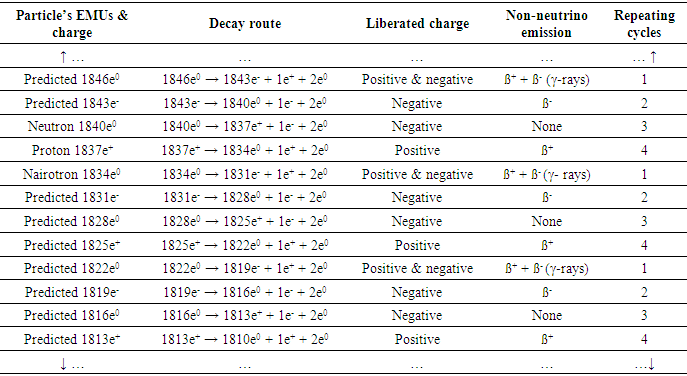
- Eq. (5) resolves charge (e) to electron mass (me) and electrostatics field (ef). Thus, conservation of electric charge is the conservation electron mass and electrostatic field. But an electrically neutral particle must have an even number of elementary charges – half positive (e+) and half negative (e-). Equally, an electrically charged particle must have excess of either of the elementary charges. By associating elementary charge and electron mass, eq. (5) predicts that an electrically neutral particle must have an even number of electron mass units (EMUs) – half positive (me+) and half negative (me-). Conversely, a particle that carries an elementary charge must have an odd number of EMUs – with unpaired me+ or me-. Whether the equation is valid or not is testable against existing experimental data. Rounding off the experimental masses of the common baryons [40] to the nearest whole EMU shows that, in agreement with the equation’s requirement, particles with even number of EMUs are electrically neutral and the old-numbered ones are electrically charged (Table 2). In other words, nature uses ‘whole positive and negative electron mass units’ as the basic building blocks of mass in in both natural and artificially generated baryons. This observation forces the conclusion that electron mass (me) is nature’s elementary mass. In this light, decimals in the experimental EMUs may be attributed to one or more factors, such human, environmental and experimental errors.
|
 | Figure 6. Hydrogen atom comprises low- and high-density quanta of ordinary mass. The masses of static nuclear positron and orbital negatron constitute the outer quantum. The densely packed me+ and me- pairs form the high-density quantum (mp0) |
|
|
5. Unification of Electrostatics and Gravity
- It has been demonstrated above, for example in Table 1, that ordinary mass is the neutral electric charge – a composite of equal numbers of positive and negative charges. Therefore, both Coulomb’s and Newton’s laws can be expressed in terms of electric charges. Coulomb describes how positive and negative charges interact; Newton describes how neutral charges interact. Thus, gravitation can be expressed as the electrostatic attraction between unlike halves of like masses M1 and M2:
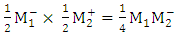 | (9) |
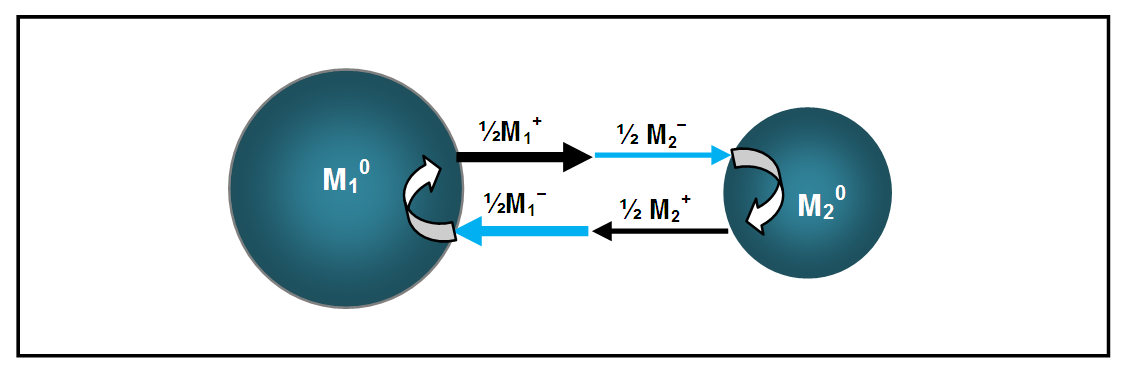 | Figure 7. Gravitational attraction is the electrostatic attraction between unlike halves of like masses. Resolving Newton’s mass (M0) into ½M+ and ½M- explains why unequal gravitational masses M10 and M20 attract with equal but opposite forces. Each mass contributes to force in either direction |
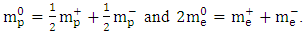 Hence, the natural (smallest) unit of ¼M1M2- is:
Hence, the natural (smallest) unit of ¼M1M2- is: 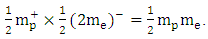 The total number of ½mpme units in ¼M1M2 is:
The total number of ½mpme units in ¼M1M2 is: 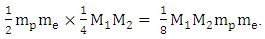 Expressed in natural units, Q1Q2 becomes Q1Q2e2 and ¼M1M2 becomes 1/8M1M2mpme. In these forms, the two types of matter that make electrostatics and gravitation different are standardized – polarized and quantized. This opens a way to standardize (unify) Coulomb’s and Newton’s equations. Coulomb shows that Fr2/QIQ2 is constant (K) and Newton shows that Fr2/MIM2 is a different constant (G). Matter in Coulomb’s equation (Q1Q2) is polarized but not quantized. On the other hand, matter in Newton’s equation (M1M2) is neither polarized nor quantized. When Coulomb’s matter is polarized and quantized, his equation becomes Fr2/Q1Q2e2 = Tc where Tc is a new electrostatic constant. Equally, when Newton’s matter is polarized and quantized, his equation becomes 8Fr2/M1M2mpme = Tn, where Tn is a new gravitation constant. Calculations based on CODATA values of physical constants [45] show that Tc equals 3.506 x 1047 NM2/C4 and Tn equals 3.506 x 1047NM2/kg4, meaning that electric charge (C4) and gravitational mass (kg4) are equivalent. The fact that constants Tc and Tn are perfectly equal proves that eq. (8) correctly unifies electric charge and ordinary mass. Equating Tc to Tn:
Expressed in natural units, Q1Q2 becomes Q1Q2e2 and ¼M1M2 becomes 1/8M1M2mpme. In these forms, the two types of matter that make electrostatics and gravitation different are standardized – polarized and quantized. This opens a way to standardize (unify) Coulomb’s and Newton’s equations. Coulomb shows that Fr2/QIQ2 is constant (K) and Newton shows that Fr2/MIM2 is a different constant (G). Matter in Coulomb’s equation (Q1Q2) is polarized but not quantized. On the other hand, matter in Newton’s equation (M1M2) is neither polarized nor quantized. When Coulomb’s matter is polarized and quantized, his equation becomes Fr2/Q1Q2e2 = Tc where Tc is a new electrostatic constant. Equally, when Newton’s matter is polarized and quantized, his equation becomes 8Fr2/M1M2mpme = Tn, where Tn is a new gravitation constant. Calculations based on CODATA values of physical constants [45] show that Tc equals 3.506 x 1047 NM2/C4 and Tn equals 3.506 x 1047NM2/kg4, meaning that electric charge (C4) and gravitational mass (kg4) are equivalent. The fact that constants Tc and Tn are perfectly equal proves that eq. (8) correctly unifies electric charge and ordinary mass. Equating Tc to Tn: 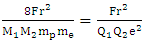 | (10) |
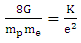 | (11) |
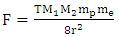 | (12) |
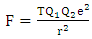 | (13) |
6. Conclusions
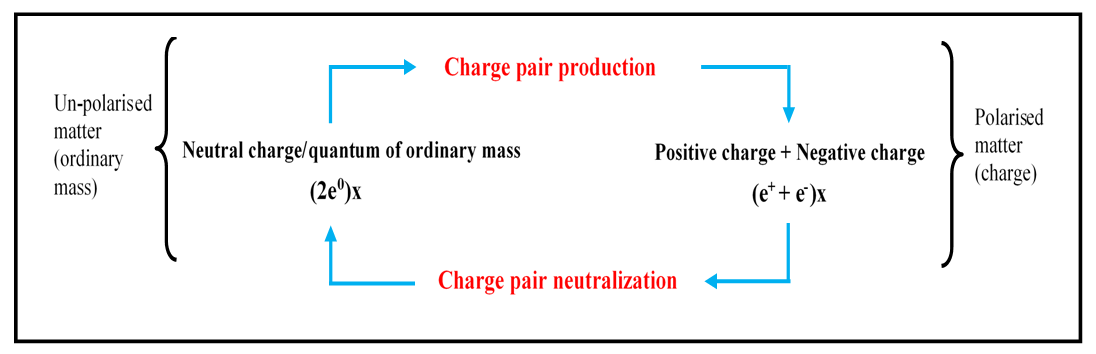
- It has been demonstrated that the macrocosmic gravitational interaction between two masses and the microcosmic electrostatic interaction between two charges unify in simple concepts and mathematical laws when electric charge and ordinary mass are interpreted in reciprocal terms. The paper has presented firm evidence that positron and negatron are the ultimate elementary blocks of matter and identified a new, stable subatomic particle. These discoveries could not have been made earlier due to lack of clarity on the fundamental nature of electric charge. A three-point paradigm shift has solved the problem, opening new vistas in physics. One, it has been demonstrated that an electron is a moving charge and a charge is a static electron. Electron and elementary charge have previously been regarded as two different entities, with the electron ‘carrying’ the charge. The confusion led to the inference that negative electrons dominate our immediate universe and that positive electrons are fringe particles. While theories – and particularly Dirac’s – demand positive-negative electron symmetry in nature, lack of such symmetry has always been enigmatic. The new insights have shown that our immediate universe has equal numbers of positive and negative electrons – moving and static – meaning that the atom’s overall electric neutrality is due to equal numbers of static positive and negative electrons. Two, the paper has proved that a grain of electricity is not an ordinary particle. Its contents, the electron mass and the electrostatic field, are either positive or negative. The current view is that positron and negatron have the same type of mass but opposite types of electric charge – though ‘electric charge’ in existing theories is ambiguous. The new insight shows that polarized stuffs, rather than the incoherent ‘charge’, give opposite electrons physical distinction. Firm theoretical and experimental proof has been presented to show that electron mass and electrostatic fields are either positive or negative. Three, it has been proved that electric charge and ordinary mass interconvert. Whereas opposite charges in motion (electrons) annihilate to energy, opposite electrons at rest (charges) neutralize to a quantum of ordinary mass. Conversely, a quantum of ordinary mass splits into a pair of opposite charges. The two processes have been named charge pair production and charge pair neutralization. It has been shown that charge pair production – the electrostatic equivalence of ‘electron pair production’ in electrodynamics – splits a quantum of ordinary mass to a pair of opposite charges. In reverse, charge pair neutralization – the electrostatic equivalence of electron pair annihilation in electrodynamics – converts a pair of opposite charges to a quantum of ordinary mass. That is, positive charge (e+) and negative charge (e-) convert to neutral charge (2e0) – which is nature’s elementary block of ordinary mass. Two vital equations have been derived from the paradigm shift: Eq. (8) and Eq. (11). Eq. (8) unifies ordinary mass and electric charge. Among other things, it reveals that electron mass is the natural elementary mass. The Equation has made it possible to establish previously unknown patterns in nuclear reactions, leading to identification of a new subatomic particle – a third, stable nucleon – which has been named the Nairotron. In addition, the Equation has predicted an infinite array of baryons in terms of their mass and electric charge. On the other hand, Eq. (12) has established the long-sought link between gravity and electricity. Broadly, two quantities of electric charge separated by distance r experience a force (F) that is directly proportional to their product and inversely proportional to the square of the distance (r-2). However, quantities of charge in Newton’s equation are neither polarized nor quantized. In contrast, quantities of charge in Coulomb’s equation are polarized but not quantized. Standardizing – polarizing and quantizing – quantities of charge in both equations reveals underlying harmony. Unification of gravity and electricity provides a theoretical blueprint for possible manipulation of gravity. Equally, the observed new patterns in nuclear reactions pave way to systematic search, identification and classification of baryons, ending decades of confusion in what is colloquially described as ‘elementary particle zoo’.
Notes
- 1. The terms ‘gravitation’ and ‘gravity’ are used interchangeably throughout this article. 2. The term ‘polarised’ is used in this article to describe the type of matter that exists either in positive or negative type.
References
| [1] | A. K. T. Assis, Deriving Gravitation from Electromagnetism, Can. J. Phys. 70, 330 - 340 (1992). |
| [2] | M. A. El-Lakany, Unification of Gravity and Electromagnetism, Journal of Physical Science and Application 7 3 15-24 (2017). |
| [3] | M. Faraday, On the Possible Relation of Gravity to Electricity, Philosophical Transactions, 141, pp. 1-6. (1851). |
| [4] | D. Gross, Einstein and the Search for Unification, Current Science 89, No. 12 (2005). |
| [5] | H. Weyl, Electricity and Gravitation, Nature 106, 800–802 (1921). |
| [6] | M. F. Spears, An Electrostatic Solution for the Gravity Force and the Value of G, Galilean Electrodynamics, 21, No. 2, pp. 23-32 (2010). |
| [7] | K. O. Greulich, A Surprisingly Close Relationship between Gravitation and Electrostatic Interactions, Fritz Lipmann Institute, Beutenbergstr. 11 D 07745 Jena, http://www.fli-leibniz.de/www_kog/ (accessed 28 April 2018). |
| [8] | E. G. Haug, Unification of Gravity and Electromagnetism, Gravity Electro Magnetism – A Probability Interpretation of Gravity, Norwegian University of Life Science (2016). |
| [9] | H. Aspden, Can Gravity Be an Electrostatic Force? Aspden Research Papers, No. 3, (2005). |
| [10] | A.K.T. Assis, Advanced Electromagnetism – Foundations, Theory and Application, World Scientific, Singapore, pp. 314-331 (1995). |
| [11] | A.K.T. Assis, Deriving Gravitation from Electromagnetism, Can. J. Phys. 70, 330 - 340 (1992). |
| [12] | R. Feynman, The Character of Physical Laws, The MIT Press, pp. 30-31(1967). |
| [13] | D.H.D. Roller, The Development of the Concept of Electric Charge: Electricity from the Greeks to Coulomb, Cambridge, MA: Harvard University Press. p. 1 (1954). |
| [14] | J. N. Mahdi, On the Nature of Electric Charge, Int. J. Phys. Sci. 9(4), pp. 54-60, (2014). |
| [15] | V. A. Etkin, Modified Coulomb Law, World Scientific News 87 163-174, (2017). |
| [16] | T. Zhang, Electric Charge as a Form of Imaginary Energy, Progress in Physics, 2, pp. 79-83 (2008). |
| [17] | L.G. Kreidik and G.P. Shpenkov, Atomic Structure of Matter-Space, Alternative Picture of the World, 1-3, Bydgoszcz, (1996). |
| [18] | R. A. Millikan, On the Elementary Electrical Charge and the Avogadro Constant, Phys Rev.2.109 (1913). |
| [19] | C. F. C. DuFay, Two Kinds of Electrical Fluid: Vitreous and Resinous – Archived 2009-05-26 at the Wayback Machine. sparkmuseum.com (1733). |
| [20] | L. J. Wang, Unification of Gravitational and Electromagnetic Forces, J Phys Chem Biophys, (2018). |
| [21] | F. Wilczek, Unification of Force and Substance. Phil. Trans. R. Soc. A 374: 20150257 (2016). |
| [22] | E.M. Purcell and D. J. Morin, Electricity and Magnetism (3rd Ed.) Harvard University, Cambridge University Press, New York pp. 5-7 (2013). |
| [23] | F. Winterberg, Teichmüller Space Interpretation of Quantum Mechanics, Gauss Press, Reno, Nevada, Zf. Naturforsch 58a, 231 (2003). |
| [24] | G. N. Golden, Avoiding Negative Probabilities in Quantum Mechanics, Journal of Modern Physics, 4, 1066-1074 (2013). |
| [25] | G. B. Stephen, and S. Ariel, The Making of Twentieth Century Science, How Theories Became Knowledge, P. 271, Oxford University Press (2015). |
| [26] | J. M. Luttinger, On Negative Mass in the Theory of Gravitation, Gravity Research Foundation, (1951). |
| [27] | H. Bondi, Negative Mass in General Relativity, Reviews of Modern Physics. 29 (3): 423–428 (1957). |
| [28] | R. M. Price, Negative Mass Can be Positively Amusing, Am. J. Phys. 61(3): 216 (1993). |
| [29] | T. Pashby, Dirac’s Prediction of the Positron: A Case Study for the Current Realism Debate, Perspectives on Science, 20, no. 4 p 440 (2012). |
| [30] | C. Anderson, The Positive Electron, Phys. Rev., 43, no. 6, pp. 491–494, Mar. 1933. |
| [31] | O. Igonkina, Inaugural Speech, Radboud University Facility Services, p. 9 (2015). |
| [32] | T. Zhang, Electric Charge as a Form of Imaginary Energy, Progress in Physics, 2 pp 79-83 (2008). |
| [33] | F. Soddy, The Complexity of Chemical Elements, The Scientific Monthly, 5, No. 5, pp. 451-462 (1917). |
| [34] | C.S. Unnikrishnan, and G. T. Gillies, The Electrical Neutrality of Atoms and of Bulk Matter, Metrologia, 41(5): S125 (2004). |
| [35] | I. Curie, and F. Joliot, β-Emission of Positive Electrons, C. R. Acad. Sci. 198, 254 (1934). |
| [36] | D. W. Engelkemeir, K. F. Flynn, and L. E., Glendenin, Positron Emission in the Decay of K40, Phys. Rev. 126 (5), 1818 (1962). |
| [37] | C.D. Simak (ed.), From Atom to Infinity, Readings in Modern Science, p.282, Minneapolis Star and Tribune Company, NY, (1964). |
| [38] | P. Blackett, Nobel Lectures, Physics 1942-1962, Elsevier Publishing Company, Amsterdam (1964). |
| [39] | J. H. Hubbell, Electron Positron Pair Production by Photons: A historical overview, Radiation Physics and Chemistry. 75 (6): 614–623 (2006). |
| [40] | S. P. Parker (ed.), Elementary Particles, McGraw-Hill Encyclopaedia of Science and Technology,' Fifth Edition, 5, McGraw-Hill Book Co., New York (1982). |
| [41] | J. Konya, and N. M. Nagy, Nuclear and Radio-chemistry, Elsevier, pp. 74–75, (2012). |
| [42] | S. Mertens, Direct Neutrino Mass Experiments, Journal of Physics: Conference Series. 718 (2): 022013 (2016). |
| [43] | P. G. Roll, R. Krotkove, and R. H. Dicke, The Equivalence of Inertial and Passive Gravitational Mass, Annals of Physics, 26, 442-517 (1964). |
| [44] | S. Carlip, Kinetic Energy and the Equivalence Principle, Am. J. Phys. 66, 409 (1998). |
| [45] | P.J. Mohr, et al. CODATA Recommended Values of the Fundamental Physical Constants, ARev. Mod. Phys, 84 1527-1605 (2012). |
 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML