-
Paper Information
- Paper Submission
-
Journal Information
- About This Journal
- Editorial Board
- Current Issue
- Archive
- Author Guidelines
- Contact Us
Journal of Nuclear and Particle Physics
p-ISSN: 2167-6895 e-ISSN: 2167-6909
2021; 11(1): 15-26
doi:10.5923/j.jnpp.20211101.03
Received: Mar. 31, 2021; Accepted: Apr. 12, 2021; Published: Apr. 25, 2021

Sensitivity Analysis of the Kinetic Parameters to Physical Parameters Variation in VVER Reactor
Heba K. Louis
Safety Engineering Department, Nuclear and Radiological Regulatory Authority (NRRA), Cairo, Egypt
Correspondence to: Heba K. Louis , Safety Engineering Department, Nuclear and Radiological Regulatory Authority (NRRA), Cairo, Egypt.
| Email: |  |
Copyright © 2021 The Author(s). Published by Scientific & Academic Publishing.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/

The effective delayed neutron fraction and the neutron generation time are the most important parameters of reactor kinetics. The main objective of this paper is to identify the influential physical parameters on kinetic parameters (sensitivity analysis). The influence of the control rod movement, temperature changes, fuel consumption, fuel enrichment, and burnable absorbers BAs on kinetic parameters is investigated. The calculations are performed using MCNP6 code together with (ENDF/B)-VII.1 library for VVER-1000. The study evidenced that fuel consumption, temperature increasing and control rod movement have the greatest influence on the effective delayed neutron fraction. The value of ßeff reduced by fuel combustion after 365 days and by rising temperature by 33.5% and 20.9% respectively. While increased to 12.11% with fully insertion of control rods. βeff parameter is not influenced by the fuel enrichment. Also, the fuel enrichment and insertion of control rods have the greatest effect on the generation time. The influence of the BAs material on the dependence of the kinetic parameters on the BAs enrichment is presented.
Keywords: Kinetic parameters, Effective delayed neutron fraction, Generation time, Power reactors, Monte Carlo code
Cite this paper: Heba K. Louis , Sensitivity Analysis of the Kinetic Parameters to Physical Parameters Variation in VVER Reactor, Journal of Nuclear and Particle Physics, Vol. 11 No. 1, 2021, pp. 15-26. doi: 10.5923/j.jnpp.20211101.03.
Article Outline
1. Introduction
- The determination of kinetic parameters is of major importance in reactor physics calculations because of its important role in the transitional reactivity analysis, safety and control of nuclear reactors. Kinetic parameters are the effective delayed neutron fraction, prompt neutron lifetime and neutron generation time.The effective fraction of delayed neutrons is a key safety parameter in nuclear reactors as it plays a scale role in the reactivity value of control bars, vacuum fractions, Doppler effect, etc. [1]. It is crucial that nuclear reactors have delayed neutrons because they act to control the rate of increase in reactor power. Without delay neutrons, the reactor's power will increase in such a magnitude and in such a short time period that significant damage will result [2]. The effective delayed neutron fraction determines the time-dependent response of the reactor. A smaller value of βeff indicates that a larger fraction of the fission neutrons appears as the prompt neutrons; therefore, the kinetic response of the reactor is quicker. Conversely, a larger value of βeff indicates that a smaller fraction of the fission neutrons appears as the prompt neutrons and the core has a slower response [3].The effective total delayed neutron fraction is designated as βeff and is normally obtained from the following relationship [4]:
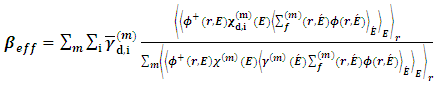 | (1) |
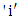 the delayed neutron family index,
the delayed neutron family index, 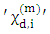 is the delayed neutron spectrum for fissile isotope m and delayed neutron family i,
is the delayed neutron spectrum for fissile isotope m and delayed neutron family i, 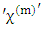 is the total neutron spectrum for fissile isotope m,
is the total neutron spectrum for fissile isotope m, 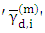 is the average value of delayed neutrons emitted from fissile isotope m and delayed neutron family i, for a given incident neutron spectrum,
is the average value of delayed neutrons emitted from fissile isotope m and delayed neutron family i, for a given incident neutron spectrum, 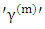 is the total neutron emitted from fissile isotope m, and
is the total neutron emitted from fissile isotope m, and 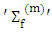 The macroscopic fission cross section of the fissile isotope m.Another important kinetic parameter that characterizes the time behavior of neutron population is the prompt neutron lifetime. The prompt neutron lifetime (lp) has an impact on the time scale of the reactor core response to reactivity changes. It is related to the neutron generation time and therefore is a measure of the time that it takes for changes in the core multiplication factor to affect the neutron population. In reactor kinetics, the prompt neutron lifetime is defined as the mean time for one neutron to be removed from the reactor i.e. it is the average time between the emission of a fission neutron and its final absorption in the active part of the reactor core. [5]Also the prompt neutron generation time (Λ) called reproduction time. It is often used to determine the dynamic response of a nuclear reactor [6]. It is defined as mean time required for one generation of neutrons to produce, due to fission, another generation of prompt neutrons or precursors [7]. The neutron generation time is related to the prompt neutron lifetime by (Λ= lp/keff) therefore is a measure of the time that it takes for changes in the core multiplication factor to affect the neutron population [8]. For a critical system (k ∼ 1), the prompt neutron lifetime is equal to the mean generation time (Λ), I. e. The time of neutron removal is equal to the time for neutron creation. Consequently, in a subcritical system, the neutron lifetime is smaller than the generation time and vice versa in a supercritical system [1].Also, it is a very important characteristic because of its own definition it is inversely proportional to macroscopic absorption cross section and consequently, to inverse 235U atom density, this can be explained from its definition [9] as shown in equation 2:
The macroscopic fission cross section of the fissile isotope m.Another important kinetic parameter that characterizes the time behavior of neutron population is the prompt neutron lifetime. The prompt neutron lifetime (lp) has an impact on the time scale of the reactor core response to reactivity changes. It is related to the neutron generation time and therefore is a measure of the time that it takes for changes in the core multiplication factor to affect the neutron population. In reactor kinetics, the prompt neutron lifetime is defined as the mean time for one neutron to be removed from the reactor i.e. it is the average time between the emission of a fission neutron and its final absorption in the active part of the reactor core. [5]Also the prompt neutron generation time (Λ) called reproduction time. It is often used to determine the dynamic response of a nuclear reactor [6]. It is defined as mean time required for one generation of neutrons to produce, due to fission, another generation of prompt neutrons or precursors [7]. The neutron generation time is related to the prompt neutron lifetime by (Λ= lp/keff) therefore is a measure of the time that it takes for changes in the core multiplication factor to affect the neutron population [8]. For a critical system (k ∼ 1), the prompt neutron lifetime is equal to the mean generation time (Λ), I. e. The time of neutron removal is equal to the time for neutron creation. Consequently, in a subcritical system, the neutron lifetime is smaller than the generation time and vice versa in a supercritical system [1].Also, it is a very important characteristic because of its own definition it is inversely proportional to macroscopic absorption cross section and consequently, to inverse 235U atom density, this can be explained from its definition [9] as shown in equation 2: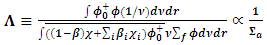 | (2) |
2. Brief Description of VVER-1000/V320 Reactor Core
- VVER-1000/V320 [15] [16] reactor core is made up from 163 hexagonal fuel assemblies of the same geometry producing 3000 MWth at full operating power. Each fuel assembly consists of 312 fuel rods containing uranium dioxide (UO2). The VVER-1000/V320 core loading pattern for the first fuel cycle consists of five fuel assembly type. The fuel assemblies’ arrangements are shown in Figure 1.
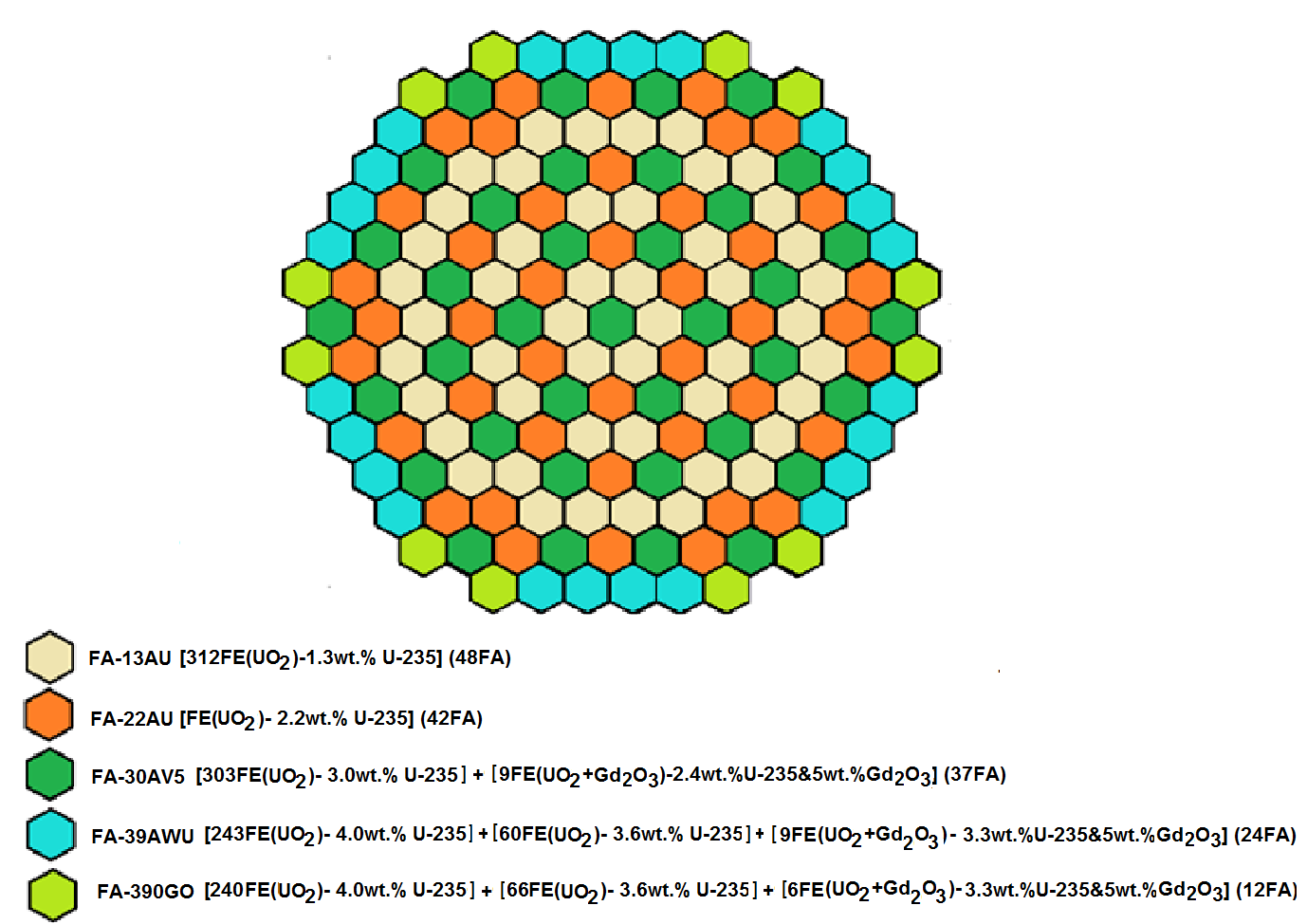 | Figure 1. Core loading pattern for first cycle of VVER-1000/V320 |
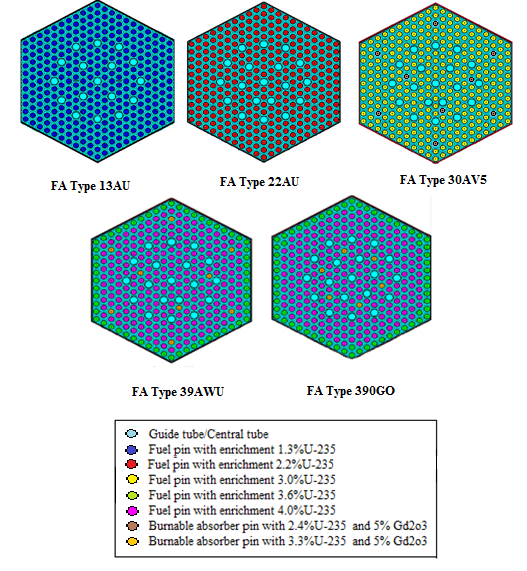 | Figure 2. Pin layout of the FA types 13AU, 22AU, 30AV5 and 39AWU |
3. Model and Calculation Procedures
- This paper has examined and analyzed the influence of several physical parameters on kinetic parameters (the effective delayed neutron fraction (βeff), and the prompt generation time (Λ)) for VVER-1000 reactor.MCNP is a general-purpose, continuous-energy, generalized-geometry, time-dependent, Monte Carlo radiation-transport code designed to track many particle types over broad ranges of energies. MCNP6 represents the culmination of a multi-year effort to merge the MCNP5 and MCNPX codes into a single product comprising all features of both. The MCNP6 code contains numerous features; one of those is to determine the delayed neutron parameters. The accuracy of the calculated delayed neutron parameters affects the accuracy of transient or dynamic condition. The superiority of the MCNP6 code can be seen in the change of the prompt neutron life time parameter
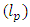 , that can't be obtained from the deterministic code so can be used in the sensitivity analysis of the delayed neutron parameter. Also, the code has been expanded to handle a multitude of particles and to include model physics options for energies above the cross-section table range, a material burnup feature, and delayed particle production.The cross section for all materials (I.e. The fuel, cladding, moderator, burnable absorber material and structural) are taken from the ENDF/B-VII.1 library (ENDF71x). Figure 3 shows the full geometric model for the VVER-1000/V320 reactor core layout in MCNP Visual Editor (VisEd). Several models are carried out according to the position of the control rods, burnup level, U-235 loading on the core level, temperature changes, presence of BAs, BAs material which used and the enrichment of BAs in the fuel.
, that can't be obtained from the deterministic code so can be used in the sensitivity analysis of the delayed neutron parameter. Also, the code has been expanded to handle a multitude of particles and to include model physics options for energies above the cross-section table range, a material burnup feature, and delayed particle production.The cross section for all materials (I.e. The fuel, cladding, moderator, burnable absorber material and structural) are taken from the ENDF/B-VII.1 library (ENDF71x). Figure 3 shows the full geometric model for the VVER-1000/V320 reactor core layout in MCNP Visual Editor (VisEd). Several models are carried out according to the position of the control rods, burnup level, U-235 loading on the core level, temperature changes, presence of BAs, BAs material which used and the enrichment of BAs in the fuel.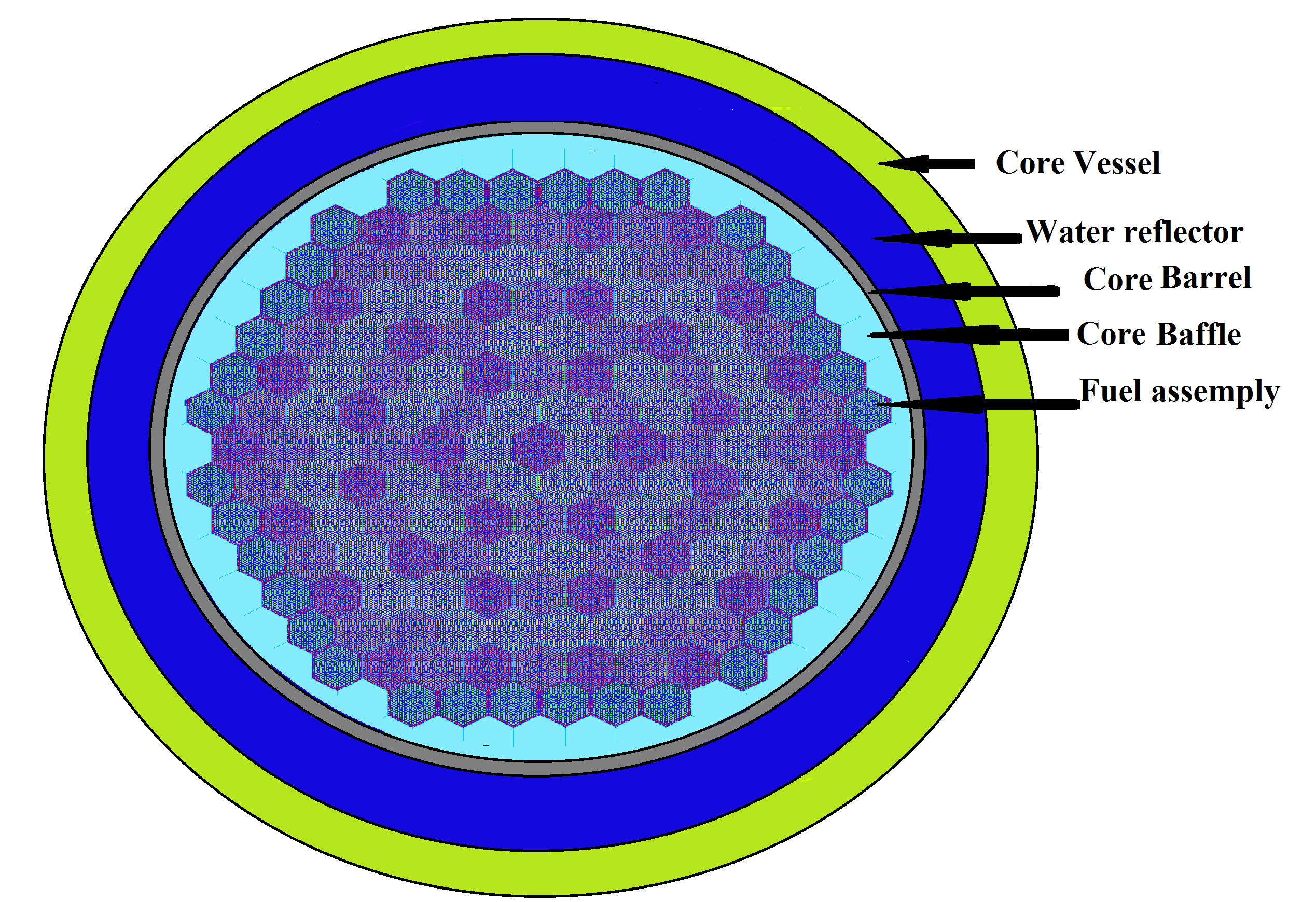 | Figure 3. Full MCNP Core Geometry Model for VVER-1000/V320 reactor |
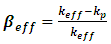 | (3) |
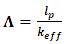 | (4) |
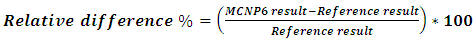 | (5) |
4. Results and Discussion
4.1. Validation of MCNP Model
- The MCNP model is validated by comparing the results of the effective delayed neutron fraction computed by the MCNP6 code with the reference data in the calculations [15]. The effective delayed neutron fraction is calculated using Eq. 3. The MCNP6 results; keff and kp as well calculated effective delayed neutron fraction are presented in table1. The standard deviation associated with criticality calculations in MCNP6 code is also presented. Moreover, the relative difference between the βeff of MCNP6 code and the mentioned reference is calculated using Eq. 5 and shown in table 1.
|
4.2. Sensitivity Studies
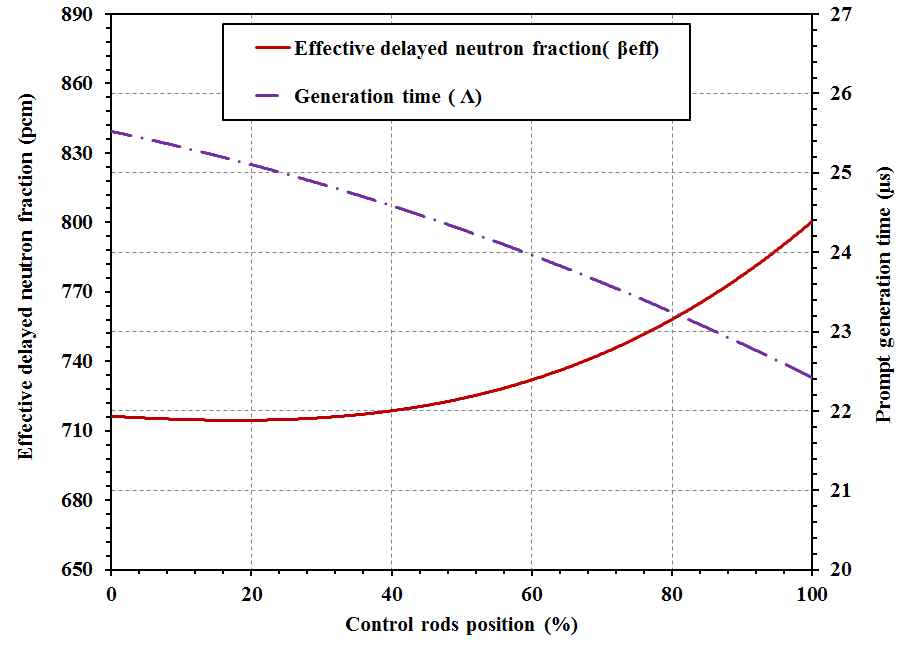
- The dependency of the kinetic parameter on the control rod movement, the temperature changes, the fuel consumption (burn up), the fuel enrichment and the integral burnable absorbers are investigated in this section. The statistical uncertainties (1 standard deviation) associated with criticality calculations in MCNP6 code were ranging from 0.00013 - 0.00025 while with prompt neutron lifetime were from 1.3E-08 - 9.6E-09. Kinetic parameters (the effective delayed neutron fraction and generation time) were calculated using Eq. 3 and Eq. 4 as mentioned previously. The dependency these parameters on the kinetic parameters are studied as follows:• The influence of control rod movement on the kinetic parameter is investigated as shown in figure 4. This figure shows the variations in the effective delayed neutron fraction and the prompt neutron generation time relative to the control rods position% from the bottom of the reactor.
 | Figure 4. Variations in kinetic parameters versus control rods position% |
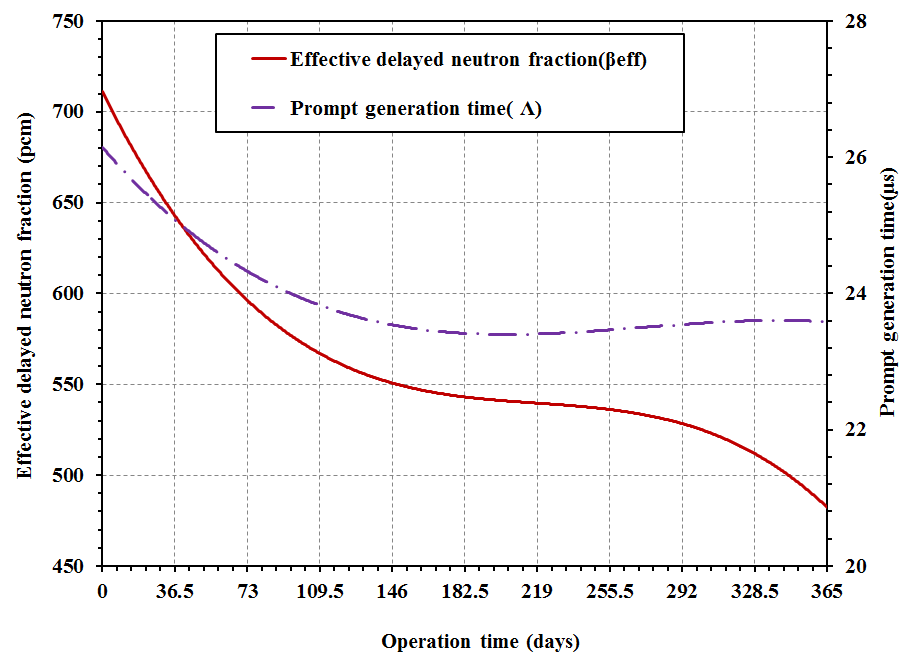 | Figure 5. Variations in kinetic parameters versus the operating time |
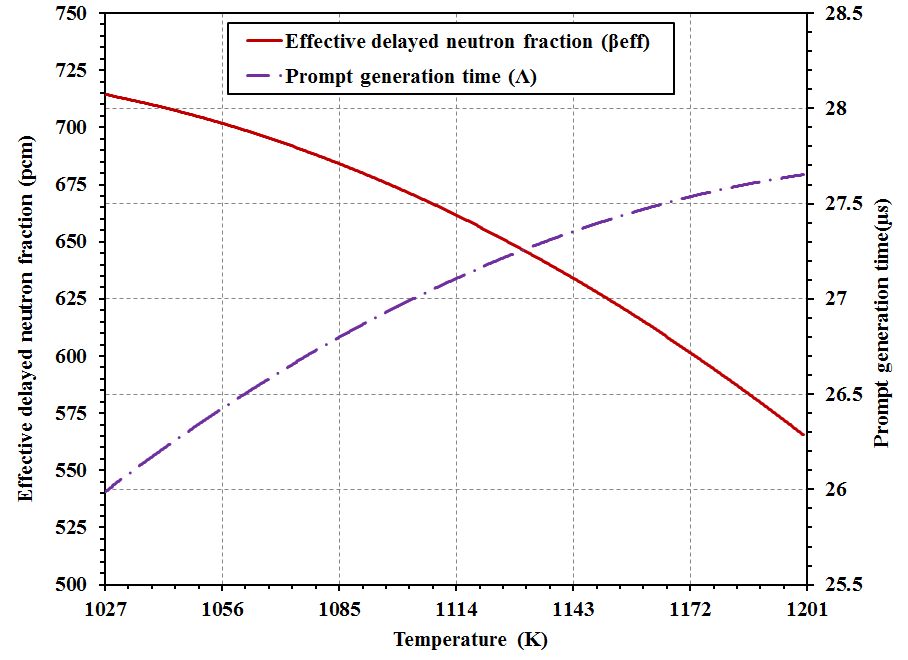 | Figure 6. Variations in kinetic parameters versus temperature rising |
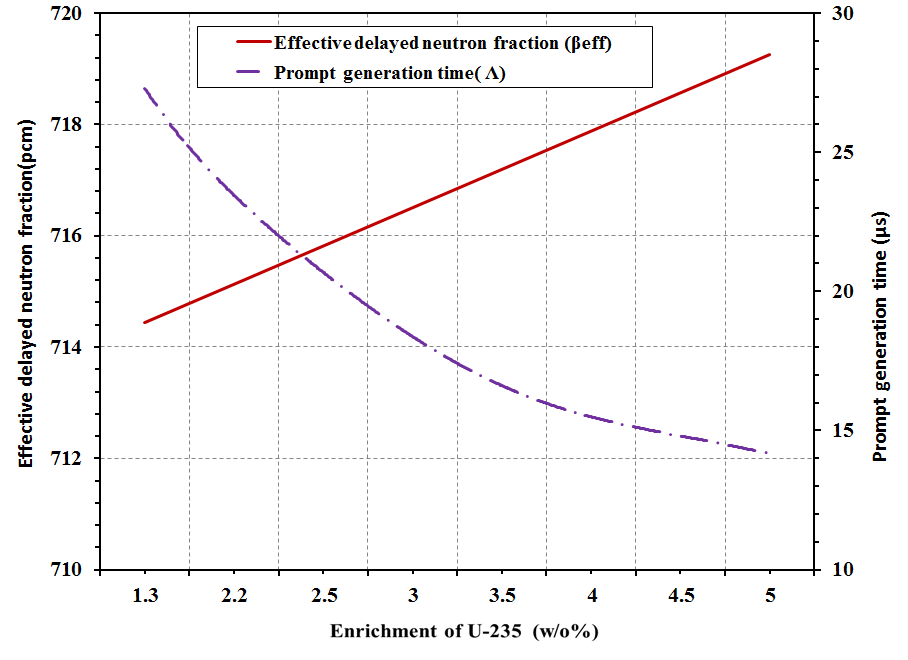 | Figure 7. Variations in kinetic parameters versus increasing fuel enrichment |
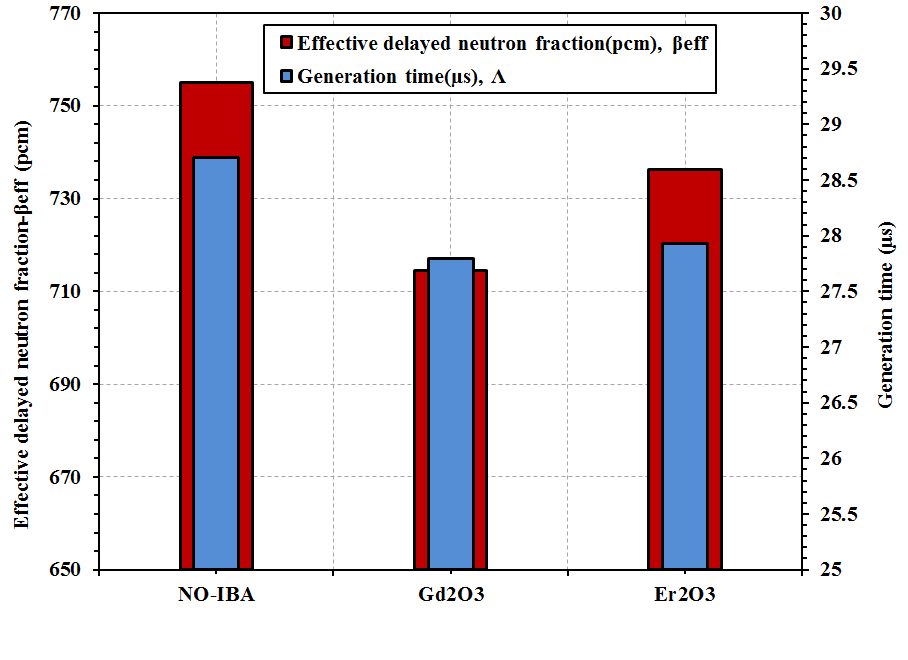 | Figure 8. Variations of VVER kinetic parameters with and without IBAs |
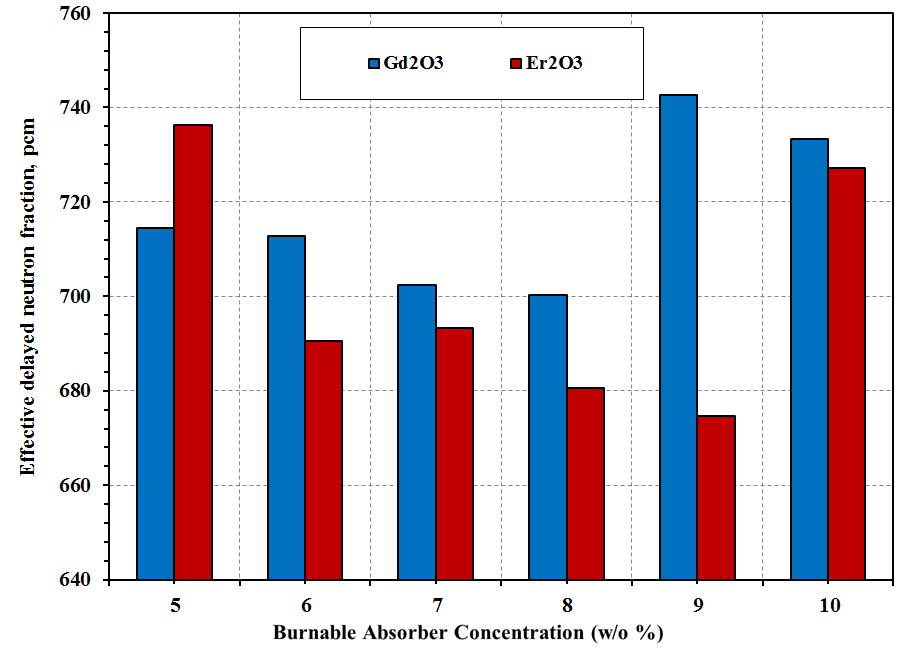 | Figure 9. Variations in effective delayed neutron fraction versus increasing BA concentration |
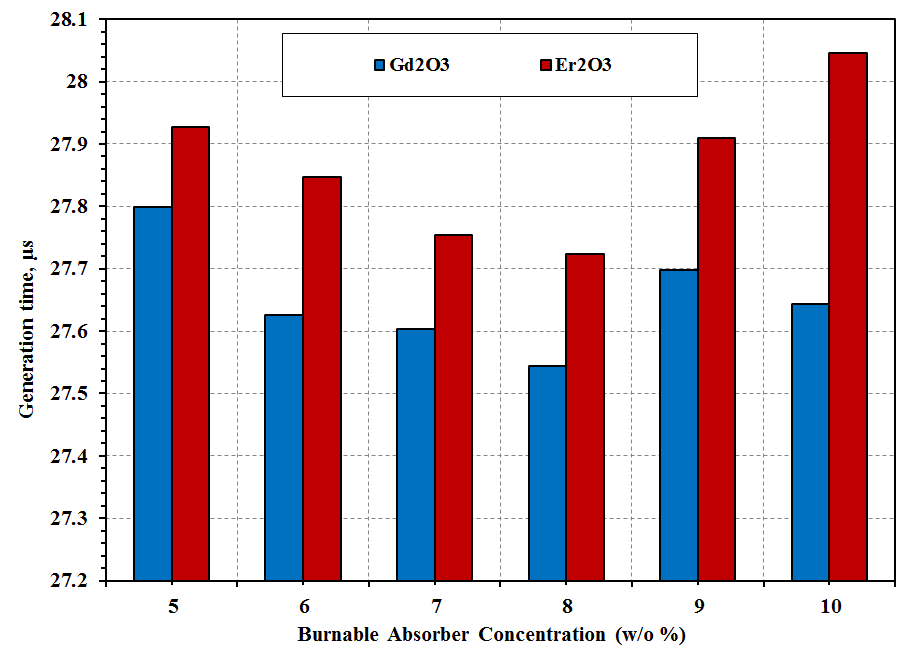 | Figure 10. Variations in generation time versus increasing BA concentration |
5. Conclusions
- Reactor kinetic parameters are very important for safety analysis in power reactors. The kinetic parameters are the effective delayed neutron fraction (βeff), and prompt neutron generation time (Λ). The effects of change in temperature, burnp, the fuel enrichment, the control rod movement and burnable absorber rods (enrichment and absorber type which used) in VVER-1000 core have been investigated using Monte Carlo code MCNP6.The sensitivity analysis evidenced that the greatest effect on the effective delayed neutron fraction was the fuel consumption, increasing temperature and control rod positions. While, lowest effect was for the fuel enrichment and the presence of BAs. The fuel enrichment and insertion of control rods have the greatest effect on the generation time while the fuel consumption, temperature changes and presence of BA have the lowest effect. The effect of changes in all parameters is detailed as follows:• The value of prompt generation time parameter decreased by fully inserted of control rods in the core by 14.6%. While the value of the effective delayed neutron fraction has increased about 12.11%.• Also, effective delayed neutron fraction, prompt neutron generation time becomes smaller as fuel consumed. The parameters have dropped up to 33.5% and 8.85% for βeff and Λ parameters respectively.• In addition, the raising of temperature produces a decrease of effective delayed neutron fraction of 20.9% and increase of generation time by 6.4%.• The Uranium enrichment produces a decrease in the generation time. The prompt neutron generation time decreased by 48.0%, βeff doesn’t show any considerable change by increasing U-235 enrichment. It means the βeff parameter is not influenced by the fuel enrichment. • Furthermore, the effective delayed neutron fraction (βeff) for the reactor without IBA is higher than for the reactor with IBAs. The Gd2O3 has smaller value for βeff than Er2O3. The Burnable absorbers cause a decrease in the βeff value by 5.4%, 2.5% for gadolinium and erbium respectively, and a decrease in the Λ value by 9.32% and 8.97% respectively.From all observations we can conclude that, the changing the control rod position, temperature, and fuel burn-up strongly affects on the effective delayed neutron fraction (βeff) and the prompt neutron generation time (Λ) which have a key role in analyzing the dynamics of nuclear reactor behavior.
 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML