-
Paper Information
- Paper Submission
-
Journal Information
- About This Journal
- Editorial Board
- Current Issue
- Archive
- Author Guidelines
- Contact Us
Journal of Nuclear and Particle Physics
p-ISSN: 2167-6895 e-ISSN: 2167-6909
2020; 10(2): 23-30
doi:10.5923/j.jnpp.20201002.01

Nonrelativistic Open String Model – Neutrino Mass and Lifetime Values
J. J. Bevelacqua
Bevelacqua Resources, Richland, WA, USA
Correspondence to: J. J. Bevelacqua, Bevelacqua Resources, Richland, WA, USA.
| Email: |  |
Copyright © 2020 The Author(s). Published by Scientific & Academic Publishing.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/

Candidate neutrino string parameters are investigated using a nonrelativistic open string model with fixed endpoints. String parameters and lifetime values are derived as a function of the neutrino mass. Large variations in string parameter and lifetime values are predicted for the various neutrino mass values utilized in this paper. The neutrino lifetime values exceed 1055 y for the 0.0001 – 1.0 eV/c2 neutrino mass range considered in this paper.
Keywords: String theory, Neutrino string parameter values, Open string model, Neutrino mass, and neutrino lifetime
Cite this paper: J. J. Bevelacqua, Nonrelativistic Open String Model – Neutrino Mass and Lifetime Values, Journal of Nuclear and Particle Physics, Vol. 10 No. 2, 2020, pp. 23-30. doi: 10.5923/j.jnpp.20201002.01.
Article Outline
1. Introduction
- String theory is an elegant mathematical formulation [1-7] that has yet to be experimentally verified. Specific particle parameter values and associated decay modes are uncertain and have been qualitatively discussed [8-28]. These uncertainties are exemplified by estimates of the neutrino mass and lifetime values [25,29,30]. This paper applies the nonrelativistic open string model proposed by the author [28] to calculate a range of neutrino string parameter and lifetime values as a function of assumed neutrino mass values.Within the Standard Model of Particle Physics, there are three generations each with a specific neutrino. These generations include the electron, muon, and tau neutrinos that are presumed to have different mass values. The nonrelativistic open string model [28] will be applied to the determination of the neutrino string parameters and lifetime values. However, the model is not sufficiently accurate to distinguish between the various neutrino types. Accordingly, this paper does not distinguish between the three generations of neutrinos, and calculates generic neutrino string characteristic and lifetime values as a function of the neutrino mass. Neutrino mass values are uncertain [25,29,30], but the KATRIN Collaboration [29] recently reported an upper limit neutrino mass of < 1.1 eV/c2 (90% C.L.). The KATRIN Collaboration results [29] significantly improved previous lifetime estimates by almost a factor of two. The magnitude of the neutrino mass and associated lifetime values have implications for both particle physics and cosmology. For particle physics, it narrows the allowed range of quasi-degenerate neutrino mass models. With respect to cosmology, a model-independent limit can be used as input for determination of the structural evolution in cosmological models. This paper defines a model to calculate the neutrino lifetime and associated string parameters as a function of neutrino mass using the nonrelativistic open string model with fixed endpoints [28]. By constraining the model to reproduce a selected neutrino mass, a set of parameters that provide an initial representation for the neutrino string and associated lifetime are derived.Determination of these string parameters and lifetime values is fraught with obvious uncertainty. The present approach provides string parameters that establish an initial, but not definitive, set as the basis to explore in future work. Subsequent work will include a string model incorporating charge, electric and magnetic fields, multiple interacting strings including loops, various boundary conditions, interaction types, gauge theories, and symmetry conditions. The deviation in string parameters from the base case values established in this paper will illuminate the dependence of the various parameters on specific string properties.
2. Nonrelativistic Open String Model Overview
- The model proposed in this paper assumes the production of cosmic strings following the big bang or during a big bang/crunch cycle of cosmic events. In this paper, it is assumed that particles result from the emission of the vibrational energy of the string. The fields associated with these particles can be derived from a number of symmetry classes. A simple example would be an Abelian-Higgs theory with a complex scalar field and a U(1) gauge field [27]. This class of fields is shown by Matsunami et al. [27] to produce a string with a lifetime, defined in Section 6.0 that is proportional to the square of the string length.Following the Abelian-Higgs field theory with a U(1) gauge approach, the decay of strings into requisite particles occurs episodically with an associated energy loss. This energy loss is associated with the neutrino mass.In previous work [28], a representative sample of string parameters for a set of baryons, leptons, and mesons were determined. This determination was based on specific mass and lifetime values for the set of selected particles that included the proton, neutron, and lambda baryons; electron, muon, and tau leptons; and charged pions and charged B mesons [28].Since the neutrino mass and lifetime values are uncertain [25,29,30], these circumstances require a somewhat different approach than utilized in [28]. Given these uncertainties, neutrino masses are assumed to vary between 0.0001 eV/c2 and 1.0 eV/c2 where 1.1eV/c2 was the upper bound noted by the KATRIN Collaboration [29]. For each assumed mass, string parameter and lifetime values are derived from the best three fits to the particle mass value. These parameter values and lifetimes are summarized in Table 1 – 5.
3. Model Parameter Specification
- The string utilized in this paper is limited to nonrelativistic velocities. The energy of the string available for neutrino decay is based on its total vibrational energy (kinetic plus potential energy). In this paper, assumed neutrino mass values are utilized to calculate the associated neutrino lifetime and string parameter values. Key model parameters include the string density, which is related to the tension, and the length, amplitude, and velocity. Bounds on the string tension (S), derived from pulsar timing measurements [22-24,27], are based on the gravitational wave background produced by decaying cosmic string loops. This bound,
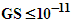 , is based on Newton’s gravitational constant (G) and is derived from simulations that ignore the field composition of the string. This would correspond to a string mass density of about 1.4x1017 kg/m. As a matter of comparison, a density of 1.4x1027 kg/m is derived from the Planck energy divided by the Planck length. Davis and Kibble [20] suggest that a string density of 1021 kg/m is an appropriate string density. These results imply that a range of density values are possible. Accordingly, the string density is permitted to vary over a range of values. Matsunami et al. [27] suggest that particle radiation is associated with a string length that is < 10-19 m. Longer lived particles that do not decay or that have extended lifetimes (e.g., protons and electrons) would be expected to have significantly longer string lengths. This assertion was also noted in [28]. In addition, cosmological strings are expected to be mildly relativistic [27]. Matsunami et al. [27] utilize values of 0.33 c and 0.6 c in their calculations. The model proposed in this paper [28] uses a nonrelativistic approach and limits the string velocity to values less than used in [27] (i.e., β ≤ 0.05).These parameter values will be used as a guide and not a specific limitation in this paper. Reasonable variations will be considered in subsequent discussion. In particular, the density is permitted to vary between 107 and 1.4x1027 kg/m. The string length is permitted to vary within the 10-21 to 1046 m. String velocity is assumed to be nonrelativistic and is limited to
, is based on Newton’s gravitational constant (G) and is derived from simulations that ignore the field composition of the string. This would correspond to a string mass density of about 1.4x1017 kg/m. As a matter of comparison, a density of 1.4x1027 kg/m is derived from the Planck energy divided by the Planck length. Davis and Kibble [20] suggest that a string density of 1021 kg/m is an appropriate string density. These results imply that a range of density values are possible. Accordingly, the string density is permitted to vary over a range of values. Matsunami et al. [27] suggest that particle radiation is associated with a string length that is < 10-19 m. Longer lived particles that do not decay or that have extended lifetimes (e.g., protons and electrons) would be expected to have significantly longer string lengths. This assertion was also noted in [28]. In addition, cosmological strings are expected to be mildly relativistic [27]. Matsunami et al. [27] utilize values of 0.33 c and 0.6 c in their calculations. The model proposed in this paper [28] uses a nonrelativistic approach and limits the string velocity to values less than used in [27] (i.e., β ≤ 0.05).These parameter values will be used as a guide and not a specific limitation in this paper. Reasonable variations will be considered in subsequent discussion. In particular, the density is permitted to vary between 107 and 1.4x1027 kg/m. The string length is permitted to vary within the 10-21 to 1046 m. String velocity is assumed to be nonrelativistic and is limited to 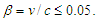 Amplitude values are restricted to be less than the string length. The lifetime value of Chacko et al. [30] was used as a lower limit for the calculated neutrino values.
Amplitude values are restricted to be less than the string length. The lifetime value of Chacko et al. [30] was used as a lower limit for the calculated neutrino values.4. Base Case String Model
- Cosmic strings have extremely large masses that greatly exceed the particle masses considered in this paper. The particle masses are assumed to be generated by the kinetic and potential energies of the vibrating string. The resulting particle mass does not depend on the total inclusive string mass. In this paper, the inherent string mass is treated as a renormalized vacuum or zero point energy with particles associated with the vibrational energy of the string.As a base case, a one-dimensional string of finite length and fixed endpoints is assumed to vibrate with peak amplitude A
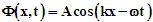 | (1) |
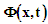 is the displacement of the string from its linear, nonoscillating state, k is the wave number, x is the position as measured from one end of the string, ω is the angular frequency, and t is the time. The string is assumed to be under tension and has mass per unit length (μ), and is fixed at x=0 and x=L where L is the nonvibrating string length. For small displacements, summing the kinetic and potential energies determines the amount of energy contained within a segment of length dx.The kinetic energy (dT) is the product of the string segment’s mass and its velocity
is the displacement of the string from its linear, nonoscillating state, k is the wave number, x is the position as measured from one end of the string, ω is the angular frequency, and t is the time. The string is assumed to be under tension and has mass per unit length (μ), and is fixed at x=0 and x=L where L is the nonvibrating string length. For small displacements, summing the kinetic and potential energies determines the amount of energy contained within a segment of length dx.The kinetic energy (dT) is the product of the string segment’s mass and its velocity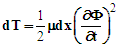 | (2) |
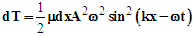 | (3) |
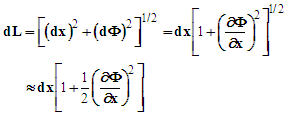 | (4) |
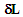 due to the tension
due to the tension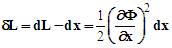 | (5) |
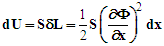 | (6) |
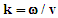 and
and 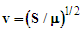 yields
yields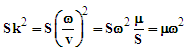 | (7) |
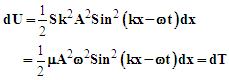 | (8) |
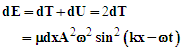 | (9) |
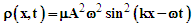 | (10) |
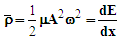 | (11) |
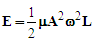 | (12) |
5. Neutrino Mass
- In order to estimate the characteristics of a string corresponding to a neutrino’s mass, a simplifying assumption is made (i.e., the string is vibrating in its fundamental frequency). This is a reasonable first approximation because the neutrino is not a resonance of a lighter particle.An application of Eq. 12 permits an estimate of neutrino’s rest mass energy (ε). This can be accomplished using the relationship between angular frequency and frequency (ν)
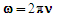 | (13) |
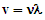 | (14) |
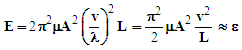 | (15) |
6. Neutrino Lifetime
- Matsunami et al. [27] provide a relationship for the string lifetime (τ)
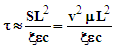 | (16) |
7. Model Assumptions and Limitations
- The neutrino lifetime and associated string parameters are derived by assuming the following:1. The model, defined in Sections 2 – 4, specifies the string parameters that characterize the neutrino.2. One episode per period is assumed which is consistent with the fundamental mode assumption of Section 5.3. The average energy lost per unit time (e.g., over a period) is the string kinetic plus potential energy. Since the string is nonrelativistic, this is assumed to be the neutrino’s rest mass. The neutrino lifetime is derived from the rest mass energy of the particle (ε) and is defined by Eqs. 15 and 16.4. Only the string kinetic plus potential energy contributes to the neutrino mass. The inherent string mass
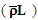 is essentially a constant (i.e., it is the vacuum or zero point energy), because the neutrino energy is much smaller than this inherent mass.5. No distinction is made for the three neutrino generations that occur in the Standard Model. The lifetime and string parameter values should be considered as a global average over the three generations of electron, muon, and tau neutrinos.6. The mass hierarchy of neutrinos is not considered or specifically evaluated. 7. Neutrino oscillations are not included in the model.8. Additional neutrino generations or the specific nature of neutrinos (i.e., Dirac or Majorana) are not considered. 9. The specific neutrino decay modes and their associated decay products are not specified or considered.
is essentially a constant (i.e., it is the vacuum or zero point energy), because the neutrino energy is much smaller than this inherent mass.5. No distinction is made for the three neutrino generations that occur in the Standard Model. The lifetime and string parameter values should be considered as a global average over the three generations of electron, muon, and tau neutrinos.6. The mass hierarchy of neutrinos is not considered or specifically evaluated. 7. Neutrino oscillations are not included in the model.8. Additional neutrino generations or the specific nature of neutrinos (i.e., Dirac or Majorana) are not considered. 9. The specific neutrino decay modes and their associated decay products are not specified or considered.8. Results and Discussion
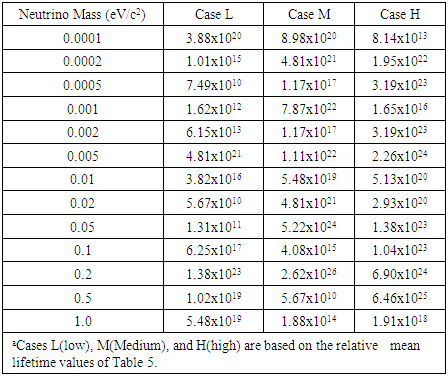
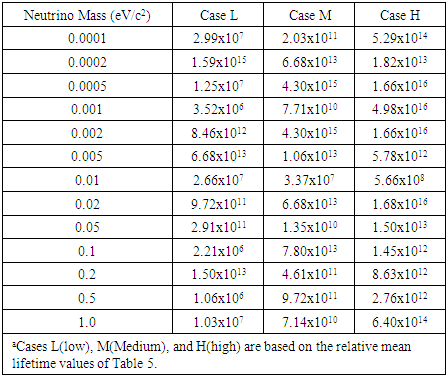
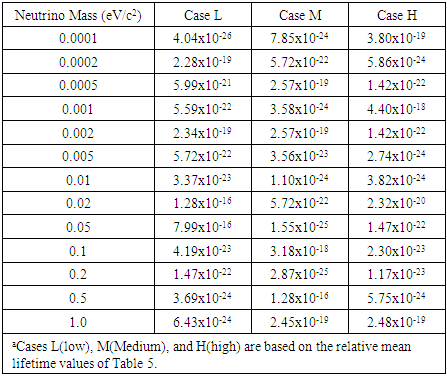
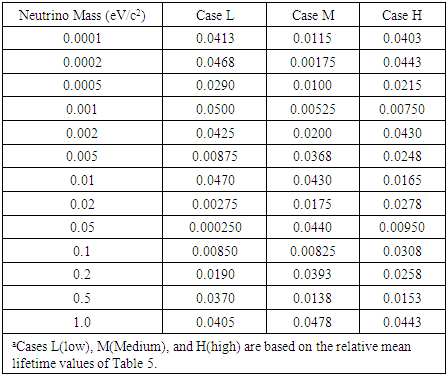
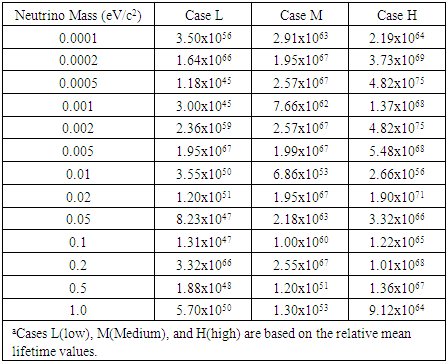
- The model results provide specific neutrino string parameter values and neutrino mean lifetime values as a function of neutrino mass. Model results suggest that long-lived neutrino lifetime values are obtained for a wide range of string parameters. The string parameters (i.e., density, length, amplitude, and velocity) supporting these lifetime values are addressed, and their variation with neutrino mass are discussed in subsequent commentary. Tables 1, 2, 3, 4, and 5 summarize, as a function of neutrino mass, the neutrino string density, length, amplitude, beta value, and lifetime values, respectively. The three best fits to the assumed neutrino mass are provided in these tables. Given the nature of the proposed calculations and associated uncertainties, a preliminary goal of fitting the particle masses and lifetimes to within 1% of their experimental values was set. This appears to be a reasonable criterion for the initial calculations.In Tables 1 – 5, the notation H (high), M (medium), and L (low) is used to label the columns of the three best parameter fits to the assumed neutrino mass value. The parameter set yielding the largest lifetime for each string mass is listed under the H column. The L (M) columns record the lowest (middle) lifetime for each of the assumed neutrino mass values.
8.1. Neutrino Masses
- The neutrino masses summarized in Tables 1 – 5 are limited to values between 0.0001 and 1.0 eV/c2 [29]. The 1.1 eV/c2 value represents the current best estimate for an upper bound to the neutrino mass [29]. The string parameters and lifetime values are calculated as a function of these assumed neutrino mass values. The neutrino mass values were fit to within 0.1% for all masses considered in Tables 1 – 5. Given the simplistic nonrelativistic, uncharged, fixed endpoint open string model, the mass results are encouraging. However, the model parameter assumptions and associated parameter ranges are still lacking in experimental verification.
8.2. String Density
- As noted in Table 1, there is significant variation in the string density as a function of neutrino mass for the L, M, and H Cases. In particular, the string density values reside within the range of 1011 – 1026 kg/m. In view of this variation, definitive conclusions regarding the string density are not possible. Therefore, a more global analysis must be utilized.To facilitate a global analysis, an averaged logarithmic string parameter (ALSP) Ω(E) is defined by the relationship:
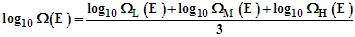 | (17) |
|
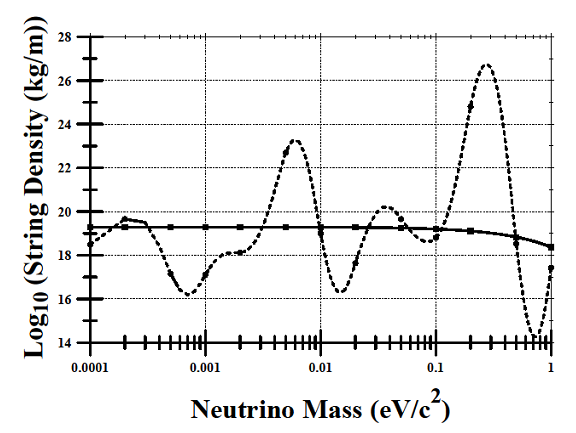 | Figure 1. Neutrino string density as a function of neutrino mass |
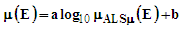 | (18) |
8.3. String Length
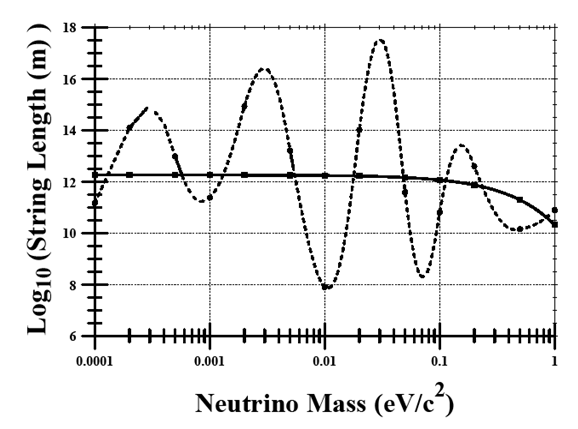
- Following [27], the string length associated with decay of unstable particles should be <10-19 m. As noted in previous discussion, this value provides an indication of an expected unstable particle string length and the results of the open string nonrelativistic model may differ.The neutrino string length values summarized in Table 2 varies over a range of 106 – 1017 m. These string length values are much larger than noted for unstable particles [27,28].For baryons, the neutron and lambda string lengths are in the range of 10-15 to 10-12 m and ≈10-19 m, respectively. A similar range of string values is found for leptons. The muon and tau string lengths are in the range of 10-19 to 10-17 m and ≈10-19 m, respectively. The meson values are 10-19 to 10-17 m and ≈10-19 m for the charged pion and charged B meson, respectively. For long-lived particles, string lengths have an increased value. Proton and electron string lengths are in the range of 106 – 1011 m and 104 – 1014 m, respectively [28]. Eq. 16 suggests that the increased proton and electron lifetime values should correspond with string lengths that are much longer than those values encountered in unstable baryons, leptons, and mesons [28]. The results summarized in Table 2 further suggest a long-lived neutrino with a lifetime as long or longer than the proton and electron. The neutrino string length results are further summarized in Fig. 2. In Fig. 2, the dashed curve represents the ALSL values derived from Table 2. The solid curve in Fig. 2 represents a linear fit to the ALSL values:
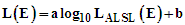 | (19) |
|
 | Figure 2. Neutrino string length as a function of neutrino mass |
8.4. String Amplitude
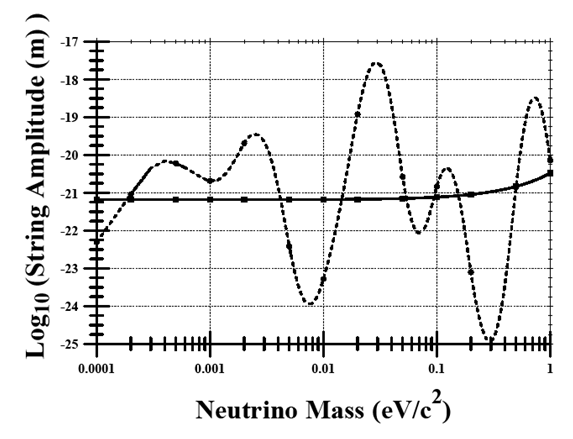
- The neutrino string amplitude summarized in Table 3 has a range between 10-26 m and 10-15 m. As noted with the other string parameters, there is considerable variability in the amplitude values. This variability is reduced using the ALSA values.Using Eq. 17, an ALSA value is calculated and is represented by the dashed curve in Fig. 3. The solid curve in Fig. 3 represents the linear fit to the ALSA values
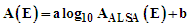 | (20) |
|
 | Figure 3. Neutrino string amplitude as a function of neutrino mass |
8.5. String Velocity
- The string velocity is restricted to β ≤ 0.05. In a previous paper [28], the baryon, lepton, and meson results suggested that there was no general velocity relationship between values of β and the particle mass or mean lifetime and associated string parameters. There is also considerable scatter in the neutrino string velocity values summarized in Table 4.The L, M, and H Case values were averaged to obtain the ASβ value:
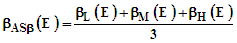 | (21) |
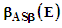 values were fit to the linear relationship
values were fit to the linear relationship 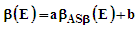 | (22) |
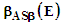 values, and the solid curve illustrates the linear fit values of Eq. 22. The averaged
values, and the solid curve illustrates the linear fit values of Eq. 22. The averaged 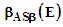 values still exhibit considerable scatter, but the linear fit suggests the neutrino velocity values lie in the range of about 0.025 c – 0.040 c. These Table 4 and Fig. 4 values are not clustered near the maximum β value (i.e., 0.05) that suggests that the model is favoring a nonrelativistic solution. This conclusion is model dependent and must be verified with a more refined approach including electromagnetic fields and other symmetry assumptions that were noted previously.
values still exhibit considerable scatter, but the linear fit suggests the neutrino velocity values lie in the range of about 0.025 c – 0.040 c. These Table 4 and Fig. 4 values are not clustered near the maximum β value (i.e., 0.05) that suggests that the model is favoring a nonrelativistic solution. This conclusion is model dependent and must be verified with a more refined approach including electromagnetic fields and other symmetry assumptions that were noted previously.
|
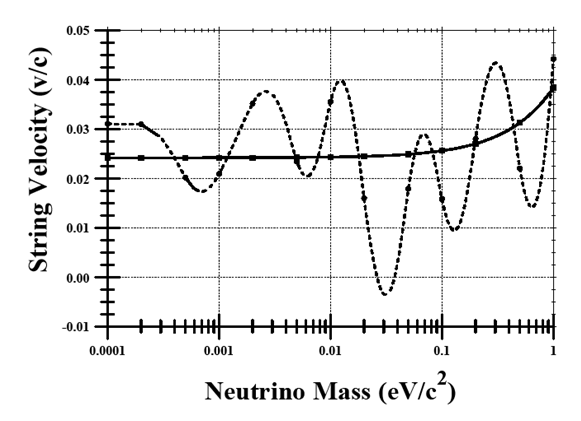 | Figure 4. Neutrino string velocity as a function of neutrino mass |
8.6. Particle Lifetime
- Following Eq. 16 and the associated discussion, the particle lifetime values are strongly dependent on the string length, tension, and particle mass. The particle mass (Eq. 15) involves multiple parameters, but the lifetime (Eq. 16) only depends on a subset of these parameters. The variation in lifetime values as a function of neutrino mass is illustrated by an examination of Table 5. As summarized in Table 5, the neutrino lifetime values vary significantly and range between 1045 and 1075 y. In the spirit of the model assumptions and limitations, the results of Table 5 were fit to the functional form of Eq. 17.
|
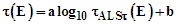 | (23) |
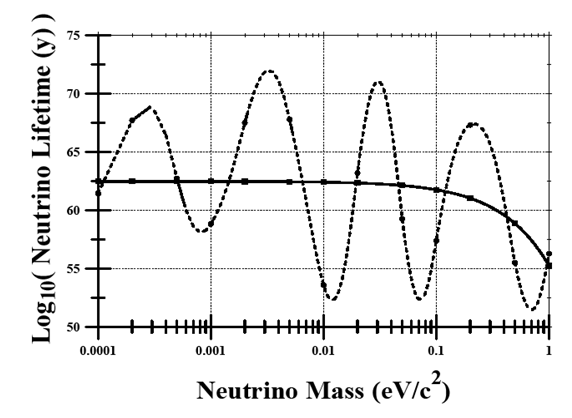 | Figure 5. Neutrino mean lifetime as a function of neutrino mass |
9. Generalization to Closed String Models
- Bagchi et al. [26] note that there is a natural emergence of an open string from a closed string given selected parameter limits. There is also a condensation of perturbative closed string modes to an open string. Bagchi et al. [26] provide an important calculation that has the potential to generalize the open string model of this paper to closed string models.
10. Conclusions
- The proposed nonrelativistic open string model with fixed endpoints provides an initial set of neutrino string parameters that yield mean lifetime values in excess of 1055 y for masses in the range of 0.0001 – 1.0 eV/c2. The derived neutrino string parameters and lifetime values are based on a simplistic open string model, and will likely change as the model becomes more complex through the inclusion of charge, electric and magnetic fields, multiple strings with loops, additional boundary conditions, and specific symmetries and gauge theories. The validity of the proposed and subsequent models will be determined by experimental verification. Experimental verification is ultimately the requirement that will determine the validity of all string theories. However, this initial set of neutrino parameters provides a base case for future investigation, development, and determination of observable string characteristics.
 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML