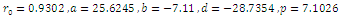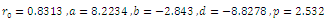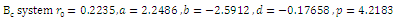| [1] | F.Halzem, A.Martin, Quarks and Leptons an Introductory Course in Modern Particle Physics, Wiley publication, 1984. |
| [2] | David Griffiths, introduction to elementary particles, Wiley publication, 1987. |
| [3] | Donald H. Perkins, Introduction to High Energy Physics, Cambridge university press, 2000. |
| [4] | B. R. Martin, Graham G Shaw, 2nd Edition, Particle Physics, the Manchester Physics Series, 1997. |
| [5] | B. H. Bransden and C. J. Joachain, Quantum Mechanics, Prentice Hall, 2000. |
| [6] | L. D. Landau and E. M. LIFSHITZ, Quantum mechanics, Butterworth Heinemann, 1981. |
| [7] | David Griffiths, introduction to elementary particle, Wiley -VCH, 2008. |
| [8] | Nouredine Zettili, Quantum Mechanics Concepts and Applications, John Wiley, 2009. |
| [9] | Cüneyt Berkdemir, theoretical concept of quantum mechanics, In Tech, 2012. |
| [10] | F Yaşuk, C Berkdemir and A Berkdemir, Exact solutions of the Schrodinger equation with non-central potential by the Nikiforov–Uvarov method, 38, 6579 (2005). |
| [11] | Yan-Fu Cheng and Tong-Qing Dai, Exact solution of the Schrödinger equation for the modified Kratzer potential plus a ring-shaped potential by the Nikiforov–Uvarov method, Phys. Scr. 75, 274 (2007). |
| [12] | [Özlem Ye, silta, PT/non-PT symmetric and non-Hermitian Pöschl–Teller-like solvable potentials via Nikiforov–Uvarov method, Phys. Scr. 75, 41 (2007). |
| [13] | H. Hassanabadi1, S. Zarrinkamar2 and A.A. Rajabi, Exact Solutions of D-Dimensional Schrödinger Equation for an Energy-Dependent Potential by NU Method, Communications in Theoretical Physics journal, 55, 541 (2011). |
| [14] | Mohammad R Setare and S Haidari, Bound states of the Dirac equation with some physical potentials by the Nikiforov–Uvarov method, Phys. Scr. 81, 015201 (5pp) (2010). |
| [15] | Birkhauser-Boston; H. Karayer, D. Demirhan, and F. Büyükkılıç, math.phys.j. 56, 063504 (2015). |
| [16] | A. Kumar Ray and P. C. Vinodkumar, J. Phys. 66, 953 (2006),; Said Laachir and Aziz Laaribi, Inter. J. of. Math. Compu. Phys. Electr. and Compu. Eng. 7(1) (2013); Hakan Ciftci, Richard L. Hall, and Nasser Saad, Phys. Rev. A 72, 022101 (2005). |
| [17] | E. J. Eichten and C Quigg, Phys. Rev. D 49, 5845 (1994); Mary Alberg, L.Wilets, Phys Lett. A 286, 7 (2001). |
| [18] | D. Ebert, R. N. Faustov and V. O. Galkin, Phys. Rev. 67, 014027 (2003); B. Ita, P. Tchoua, E. Siryabe, G. E. Ntamack, Inter. J. of Theor. And Math. Phys. 4(5), 173 (2014); H. Goudarzi 1 and V. Vahidi, Adv. Studies Theor. Phys. 5(10), 469 (2011). |
| [19] | R. Kumar and F. Chand, Commun. Theor. Phys. 59, 528 (2013); M. Abu-Shady, Inter. J. of Appl. Math. and Theor. Phys. 2(2), 16 (2016). |
| [20] | A. Al-Jamel and H. Widyan, Appl. Phys. Rese. 4, 94 (2013); CHANG ChaoHsi and WANG GuoLi, SCI. chinese 53(11), 2025 (2010). |
| [21] | N. V. Masksimenko and S. M. Kuchin, Russ. Phy. J. 54, 57 (2011); E. Eichten, T. Kinoshita, K. Gottfried, et al., Phys. Rev. Lett. 34, 369 (1975). |
| [22] | Z. Ghalenovi, A. A. Rajabi, A. Tavakolinezhad, Mod. Phys. inter. J. 5(6), 1250057 (2012); Juan-Juan Niu, a Lei Guo, b, Hong-Hao Ma,c, Shao-Ming Wang, Eur. Phys. J. C 78, 657 (2018). |
| [23] | S. M. Kuchin and N. V. Maksimenko, Univ. J. Phys. Appl. 7, 295 (2013); R. Faccini, BABAR-CONF-07/035 SLAC-PUB-13080. |
| [24] | R. Kumar and F. Chand, Phys. Scr. 85, 055008 (2012); Yang Li, Pieter Maris, and James P.Vary, Phys. Rev. D 96, 016022 (2017). |
| [25] | J. Beringer et al. [Particle Data Group], Phys. Rev. D 86, 1 (2012); Byungsik Hong, Overview of quarkonium production in heavy-ion collisions at LHC, published by EDP Sciences (2015). |
| [26] | Yu-Qi Chen 1'3, Yu-Ping Kuang 1'2'3, General relations of heavy quark-antiquark potentials induced by reparameterization invariance, Z. Phys. C 67, 627 (1995). |
| [27] | Q ¯ Q (Q ∈ {b, c}) spectroscopy using Cornell potential, N. R. Soni,∗ B. R. Joshi,† R. P. Shah,‡ H. R. Chauhan,§ and J. N. Pandya, European Physical Journal C 78(7), (2017). |
| [28] | D. Ebert, R. N. Faustov, and V. O. Galkin, Spectra of heavy mesons in the Bethe-Salpeter approach,Eur. Phys. J. C 71, 1825 (2011). |
| [29] | W.-J. Deng, H. Liu, L.-C. Gui, and X.-H. Zhong, Properties of Low-Lying Charmonium States in a Phenomenological Approach, Phys. Rev. D 95, 034026, 1608.00287 (2017). |
| [30] | C. S. Fischer, S. Kubrak, and R. Williams, Spectra of heavy mesons in the Bethe-Salpeter approach,Eur. Phys. J. A 51, 1409.5076, 10 (2015). |
| [31] | B.-Q. Li and K.-T. Chao, Higher Charmonia and X,Y,Z states with Screened Potential, Phys. Rev. D 79, 094004 (2009). |
| [32] | B.-Q. Li and K.-T. Chao, Bottomonium Spectrum with Screened Potential, Commun. Theor. Phys. 52, 0909. 1369, 653 (2009). |
| [33] | N. Devlani, V. Kher, and A. K. Rai, Masses and electromagnetic transitions of the Bc mesons, Eur. Phys. J. A 50, 154 (2014). |
| [34] | S. Godfrey, Phys. Rev. D 70, Spectroscopy of Bc mesons in the relativized quark model, 054017, hep-ph/0406228, (2004). |
| [35] | A. P. Monteiro, M. Bhat, and K. B. Vijaya Kumar, cb¯ spectrum and decay properties with coupled channel effects, Phys. Rev. D 95, 1608.05782, 054016 (2017). |


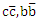 and
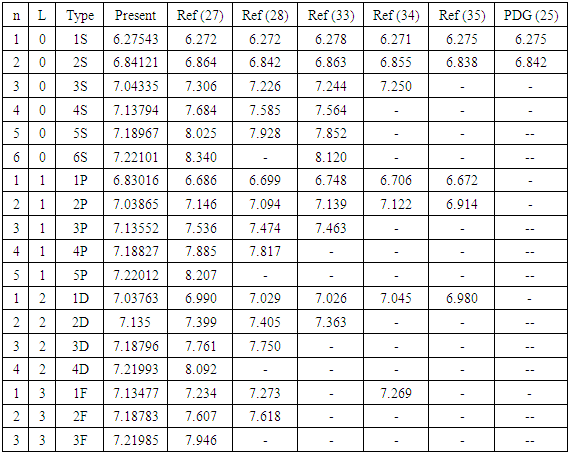
and 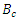 meson in the quark model framework with phenomenological potentials is motivated by quantum chromodynamics (QCD). It is found that analysis of the mass spectra of these systems is effectively given by the nonrelativistic Schrödinger's equation. There are several methods which are used to solve Schrödinger's equation with a general polynomial potential one of them is the Nikiforov-Uvarov (NU) method. It’s one of the effective methods which gives the energy eigenvalues and eigenstates for our potential. The results obtained are in good agreement with the experimental data and are better than previous theoretical studies.
meson in the quark model framework with phenomenological potentials is motivated by quantum chromodynamics (QCD). It is found that analysis of the mass spectra of these systems is effectively given by the nonrelativistic Schrödinger's equation. There are several methods which are used to solve Schrödinger's equation with a general polynomial potential one of them is the Nikiforov-Uvarov (NU) method. It’s one of the effective methods which gives the energy eigenvalues and eigenstates for our potential. The results obtained are in good agreement with the experimental data and are better than previous theoretical studies.
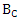 Meson Mass Spectrum
Meson Mass Spectrum
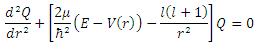
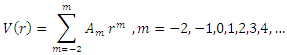
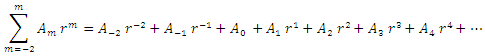
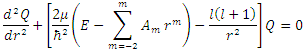
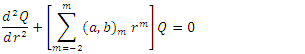
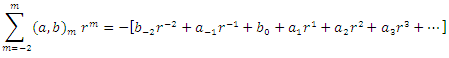
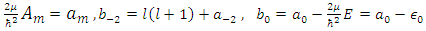
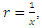 and substituting in equation (5), we get
and substituting in equation (5), we get 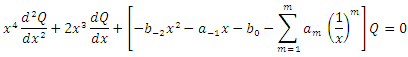
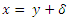
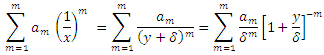
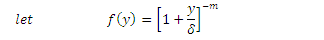
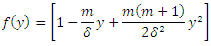
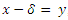 , we get
, we get 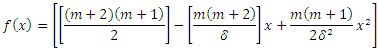
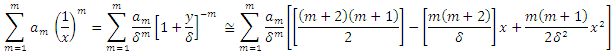
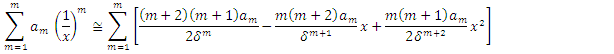
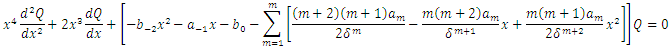
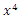 where
where 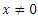 to obtain,
to obtain,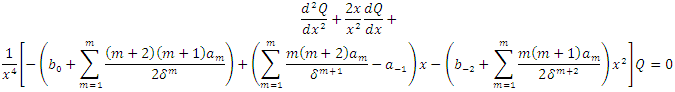
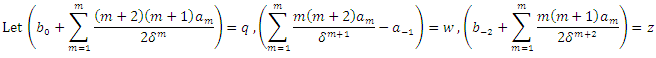
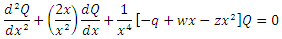
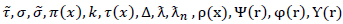 are symbols used in the Nikiforov-Uvarov (NU) method.
are symbols used in the Nikiforov-Uvarov (NU) method.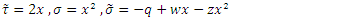
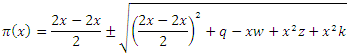
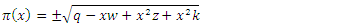
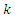 which make the square root in equation (21) as a quadratic term
which make the square root in equation (21) as a quadratic term 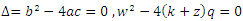
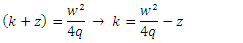
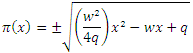
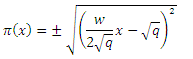
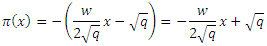
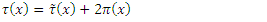
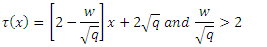
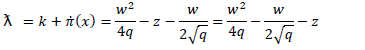
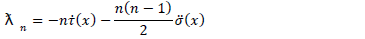
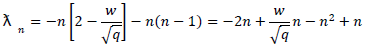
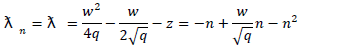
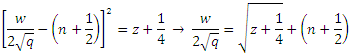
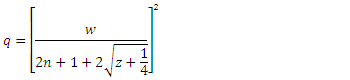
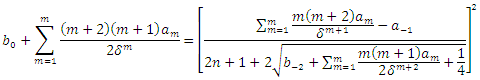
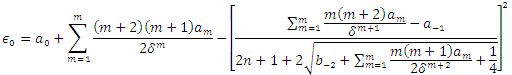
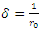 and substituting in equation (36), we obtain
and substituting in equation (36), we obtain 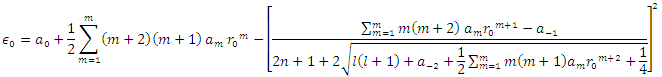
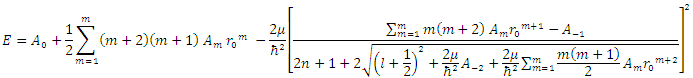
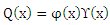
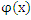
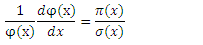
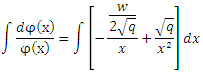
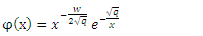
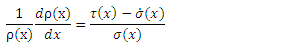
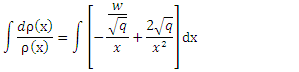

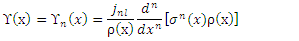
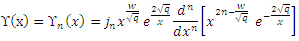
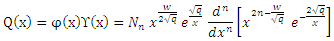
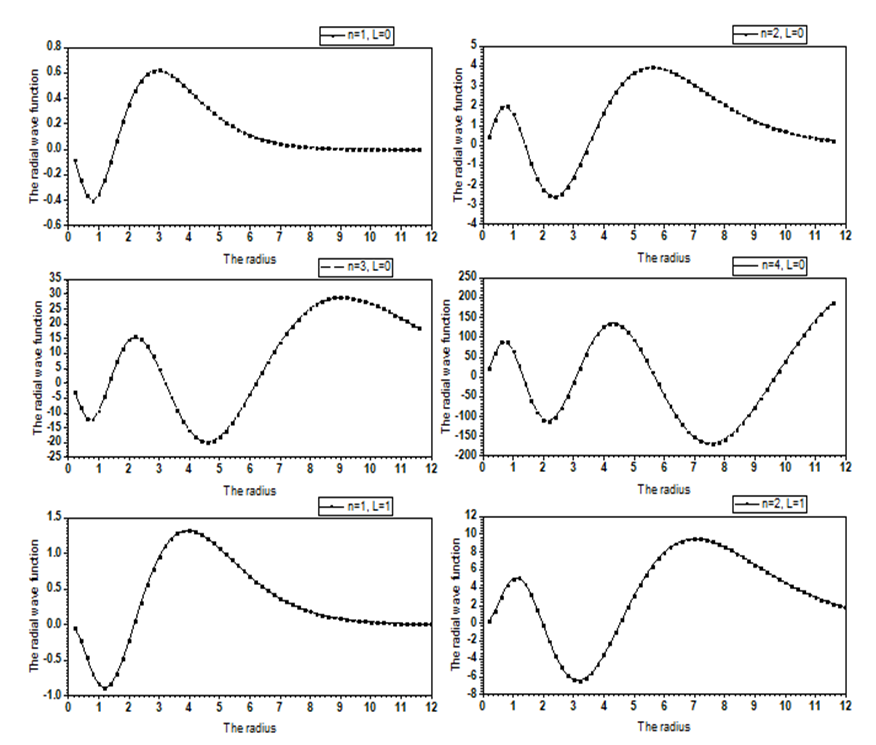
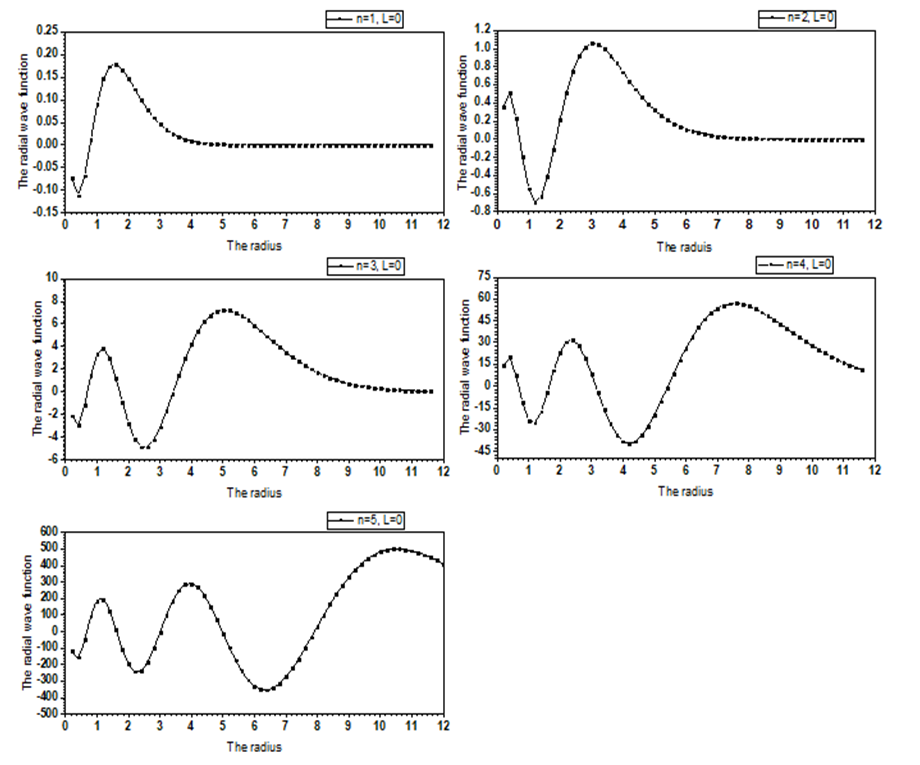
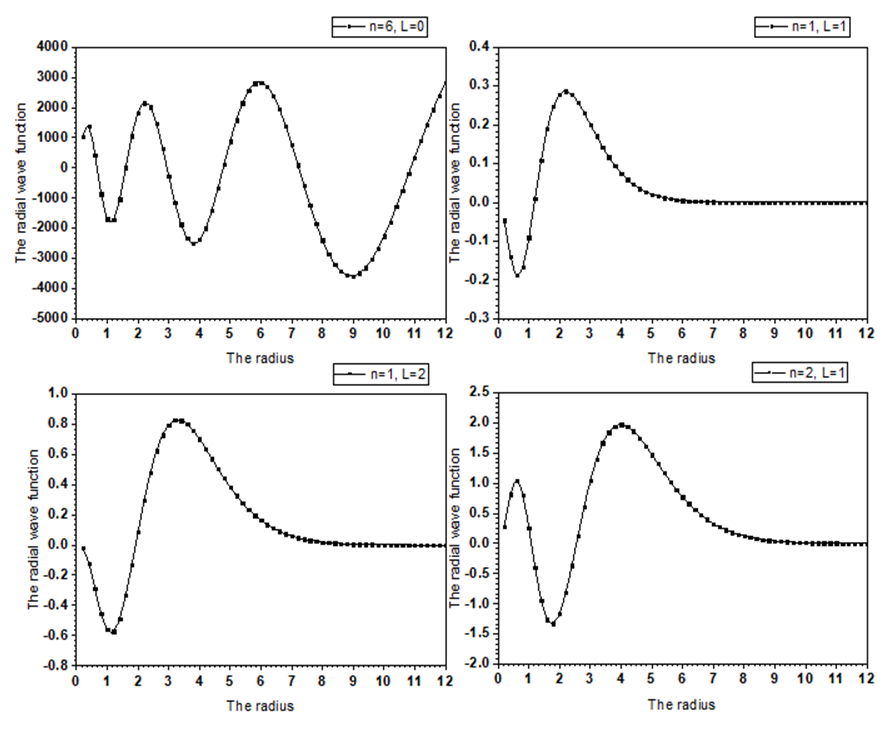
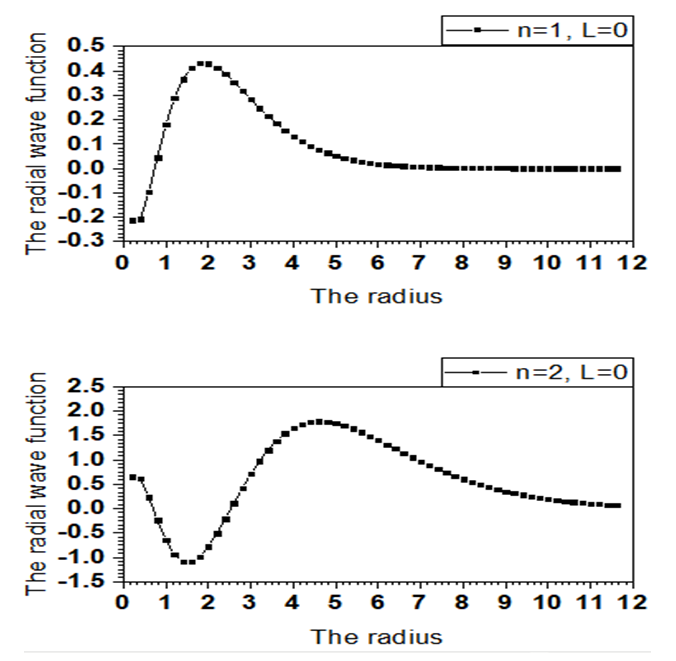
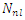 is a normalization constant.So, the radial wavefunction of Schrödinger equation (1) for a polynomial potential is
is a normalization constant.So, the radial wavefunction of Schrödinger equation (1) for a polynomial potential is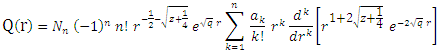
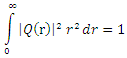
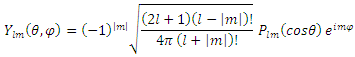
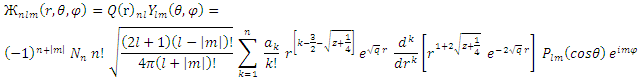
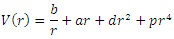
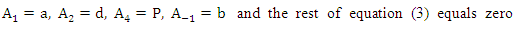
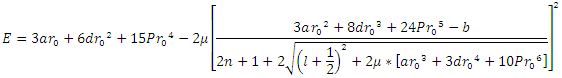
 meson. The mass spectra equation is
meson. The mass spectra equation is 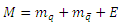
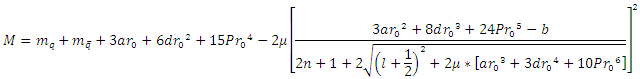
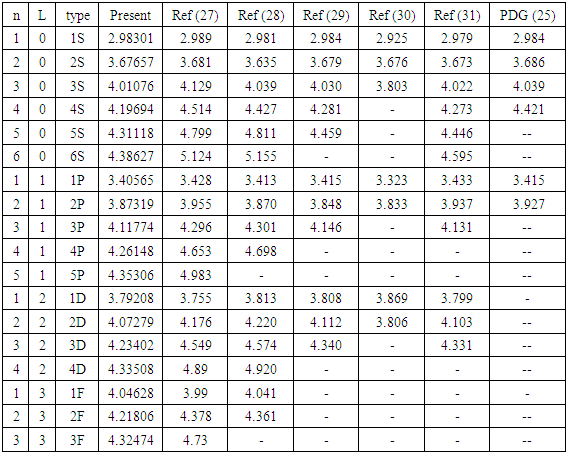
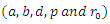 which will be obtained from the experimental data.In the case of charmonium
which will be obtained from the experimental data.In the case of charmonium 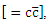 the rest mass equation is
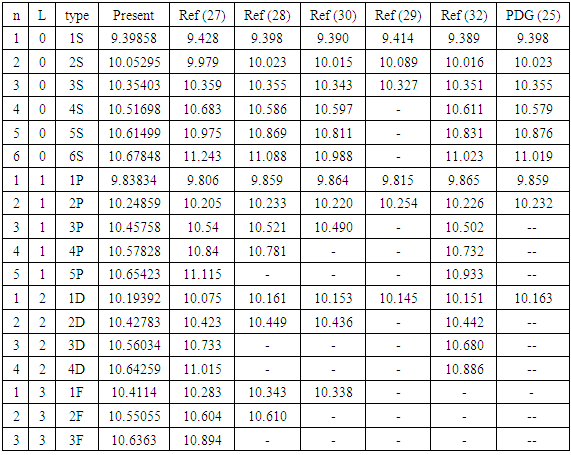
the rest mass equation is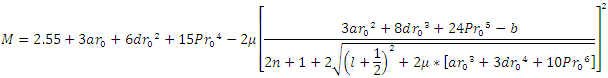
 , the rest mass equation is
, the rest mass equation is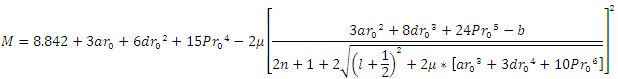
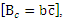 the rest mass equation is
the rest mass equation is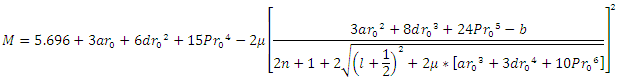
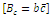 system
system Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML