| [1] | A. O. Barut and J. Kraus, Resonances in e+,e− system due to anomalous magnetic moment interactions, Physics Letters B59,175, 1975. |
| [2] | A. O. Barut and J. Kraus, Solution of the Dirac equation with Coulomb and magnetic moment interactions, Journal of Mathematical Physics 17, 506, 1976. |
| [3] | A. O. Barut and J. Kraus, Form-factor corrections to superpositronium and short-distance behavior of the magnetic moment of the electron., physical review D 16, 161, 1977. |
| [4] | Alberto Sadum and Masoud Asadi-Zeydabadi, A Study of the Two-body Problem with Magnetic Interactions, Journal of physics, astrophysics and physical cosmology, 3, Issue 1, 2009. |
| [5] | Bruno Gruber, two body problems with magnetic interaction "Symmetries in Science VIII", Springer Science, 1994. |
| [6] | M. Naghdi, Nucleon-Nucleon Interaction: A Typical/Concise Review, arXiv:nucl-th/0702078. |
| [7] | Bernard Schaeffer, Electromagnetic Theory of the Nuclear Interaction, World Journal of Nuclear Science and Technology, 6, no.4, 199, 2016. |
| [8] | F.BLOCH, Le moment magnétique du neutron, Annales de l'institut Henri Poincaré, 8, no. 1, 63, 1938. |
| [9] | Richard P Feynman; Robert B Leighton, Matthew Linzee Sands, the Feynman lectures on physics, San Francisco, Pearson addition Wesley, 2006. |
| [10] | Rajmund Krivec, Mitja Rosina, Bojan Golli and Simon Širca, Few-Body Problems in Physics, Springer Wein New York, 2003; W.T. Grandy, book: Relativistic Quantum Mechanics of Leptons and Fields, Springer Science & Business Media, 1990. |
| [11] | A. O. Barut and G.strobel, Large Magnetic Moment Effects at High Energies and Composite Particle Models, Field Theory in Elementary Particles. Studies in the Natural Sciences (A Series from the Center for Theoretical Studies), Springer, Boston, 19, 323, 1983. |
| [12] | C. Prion, F. Reuse, Relativistic dynamics for the spin 1/2 particle, Helvetica Physica Act, 51, 146, 1978. |
| [13] | F. Reuse, A new relativistic model for the hydrogen atom, Helvetica Physica Acta, 51, 157, 1978. |
| [14] | A. O. Barut, lectures on magnetic interaction of stable particles and magnetic resonances, mathematical reviews, American mathematical society, P 4933, 1982. |
| [15] | A. O. Barut, Magnetic resonances between massive and massless spin‐ 1/2 particles with magnetic moments, Journal of Mathematical Physics 21, 568, 1980. |
| [16] | A. O. Barut, radial equations for Dirac particle with anomalous magnetic moment in a dipole field, quantum theory groups, fields and particles, mathematical physics studies, 1983. |
| [17] | G. Aad et al. (ATLAS Collaboration), Search for magnetic monopoles and stable particles with high electric charges in 8 TeV pp collisions with the ATLAS detector, Phys. Rev. D 93, 052009, 2016. |
| [18] | The MoEDAL collaboration, Search for magnetic monopoles with the MoEDAL prototype trapping detector in 8 TeV proton-proton collisions at the LHC, Journal of High Energy Physics, 8, 67, 2016. |
| [19] | M. W. Ray, E. Ruokokoski, S. Kandel, M. Möttönen & D. S. Hall, Observation of Dirac monopoles in a synthetic magnetic field, Nature, 505, 657, 2014. |
| [20] | C. Castelnovo, R. Moessner & S. L. Sondhi, Magnetic monopoles in spin ice, Nature 451, 42, 2008. |
| [21] | A.O. Barut, R. Rączka, Two-Fermion Equation with Form-Factors and Electromagnetic High Mass Resonances, acta physica polonica B10, 687, 1979. |
| [22] | M.M. Bakri, H.M.M. Mansour, The Relativistic Two-Fermion Equations (I), acta physica polonica B11, 413, 1980. |
| [23] | M.M. Bakri, H.M.M. Mansour, The Relativistic Two-Fermion Equations (II), acta physica polonica B11, 543, 1980. |
| [24] | E. E. Salpeter and H. A. Bethe, A Relativistic Equation for Bound-State Problems, Physical Review, 84, 1232, 1951. |
| [25] | W. Królikowski, J. Rzewuski, Covariant one-time formulation of the many-body problem in quantum theory, Il Nuovo Cimento, 2, Issue 2, 203, 1955. |
| [26] | W. Królikowski, J. Rzewuski, On “ potentials ” in the theory of quantized fields, Il Nuovo Cimento, 3, Issue 2, 260, 1956. |
| [27] | W. Królikowski, J. Rzewuski, One-time formulation of the relativistic two-body problem. Separation of angular variables, Il Nuovo Cimento, 4, Issue 5, 975, 1956. |
| [28] | W. Królikowski, J. Rzewuski, Remarks on composite and unstable objects in quantum field theory, Il Nuovo Cimento B, 25, Issue 2, 739, 1975. |
| [29] | M. Hossein Partovi, New treatment of the bound-state problem in quantum field theory, physical review D 12, 3887, 1975. |
| [30] | H. Suura, Relativistic Two-Body Wave Equation, and Meson Spectrum, Physical Review Letters, 38, 636,1977. |
| [31] | G. Preparata,N.S .Craigie, A space-time description of quarks and hadrons, Nuclear Physics B 102, Issue 3, 478, 1976. |
| [32] | A. O. Barut, M. Berrondo, and G. García‐Calderón, Narrow resonances as an eigenvalue problem and applications to high energy magnetic resonances: An exactly soluble model, Journal of Mathematical Physics 21, 1851, 1980. |
| [33] | H. M. M. Mansour, and H. J. W. Müller‐Kirsten, Perturbative technique as an alternative to the WKB method applied to the double‐well potential, Journal of Mathematical Physics 23, 1835, 1982. |
| [34] | H. M. M. Mansour and H. J. W. Müller-Kirsten, Matching of WKB solutions to other solutions, physical review, D 24, 1033, 1981. |
| [35] | Andrzej A.Skorupski, Reports on Mathematical Physics, Improved higher order phase-integral approximations of the JWKB type in the vicinity of zeros and singularities of the “wave number”, 17, Issue 2, 161, 1980. |
| [36] | Nouredine Zettili, Quantum Mechanics Concepts and Applications, John Wiley, 2009. |
| [37] | Cüneyt Berkdemir, Theoretical concept of quantum mechanics, In Tech, 2012. |
| [38] | F. Nikiforov and V. B. Uvarov, Special Functions of Mathematical Physics, Birkhäauser, Basel, Switzerland, 1988. |
| [39] | E. Eichten, K. Gottfried, T. Kinoshita, J. Kogut, K. D. Lane, and T. M. Yan, “Spectrum of charmed quark-antiquark bound states,” Physical Review Letters, 34, no. 6, 369, 1975. |
| [40] | S. M. Kuchin and N. V. Maksimenko, “Theoretical Estimations of the Spin – Averaged Mass Spectra of Heavy Quarkonia and Bc Mesons,” Universal Journal of Physics and Application, 7, 295, 2013. |
| [41] | S. Laachir and A. Laaribi, “Exact Solutions of the Helmholtz equation via the Nikiforov-Uvarov Method,” International Journal of Mathematical, Computational, Physical, Electrical and Computer Engineering, 7, no. 1, 2013. |
| [42] | H. Ciftci, R. L. Hall, and N. Saad, “Iterative solutions to the Dirac equation,” Physical Review A: Atomic, Molecular and Optical Physics, 72, no. 2, part A, 022101, 2005. |
| [43] | M. Alberg and L. Wilets, “Exact solutions to the Schrödinger equation for potentials with Coulomb and harmonic oscillator terms,” Physics Letters A, 286, no. 1, 7, 2001. |
| [44] | B. Ita, P. Tchoua, E. Siryabe, and G. E. Ntamack, “Solutions of the Klein-Gordon Equation with the Hulthen Potential Using the Frobenius Method,” International Journal of Theoretical and Mathematical Physics, 4, no. 5, 173, 2014. |
| [45] | H. Goudarzi and V. Vahidi, “Supersymmetric approach for Eckart potential using the {NU} method,” Advanced Studies in Theoretical Physics, 5, no. 9, 469, 2011. |
| [46] | N. V. Masksimenko and S. M. Kuchin, “Determination of the mass spectrum of quarkonia by the Nikiforov–Uvarov method,” Russian Physics Journal, 54, no. 57, 54, 2011. |
| [47] | Hesham Mansour and Ahmed Gamal, Bound State of Heavy Quarks Using a General Polynomial Potential, Advances in High Energy Physics, 1, Article ID 7269657, 2018. |



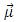 [11], or alterentivly, a charged spin 1/2 particle of mass m and magntic moment
[11], or alterentivly, a charged spin 1/2 particle of mass m and magntic moment 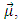 in the field of a fixed charge [12,13]. In both cases the radial equation has the form
in the field of a fixed charge [12,13]. In both cases the radial equation has the form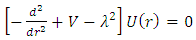
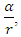 by
by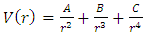
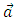 to the particle, then additional terms are added to equation (2).Further models may also treat the magnetic moment of both particles. The potential in equation (2) is treated in atomic phenomena as well as in the quark models as a perturbation. This is justified only if the energies are of the order of the Coulomb energies. At very short distances, the form of the potentials is quite uncertain, and these potentials must be modified by form factors. Form factors must then be calculated in a non-perturbative and self-cosistent method from the wave functions which are localized around each well. In the next section, we will sketch some of the physical problems in which case such a form of this potential appears.In section (3) we will give a short description of the relativistic two -body equation which is used to describe two-body systems, and finally, in section (4), we will show a method for solving equation (1) over the whole range of the independent variable.
to the particle, then additional terms are added to equation (2).Further models may also treat the magnetic moment of both particles. The potential in equation (2) is treated in atomic phenomena as well as in the quark models as a perturbation. This is justified only if the energies are of the order of the Coulomb energies. At very short distances, the form of the potentials is quite uncertain, and these potentials must be modified by form factors. Form factors must then be calculated in a non-perturbative and self-cosistent method from the wave functions which are localized around each well. In the next section, we will sketch some of the physical problems in which case such a form of this potential appears.In section (3) we will give a short description of the relativistic two -body equation which is used to describe two-body systems, and finally, in section (4), we will show a method for solving equation (1) over the whole range of the independent variable.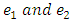 with magntic moments
with magntic moments 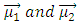 respectivly the Hamiltonain in this case is
respectivly the Hamiltonain in this case is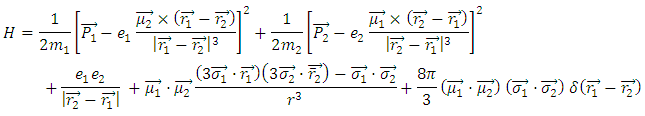
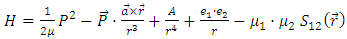
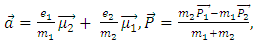
 And
And 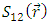 is the so-called tensor and dipole-dipole interaction potential In some special cases, the problem becomes easier to solve e.g.a)
is the so-called tensor and dipole-dipole interaction potential In some special cases, the problem becomes easier to solve e.g.a) 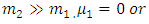 b)
b) 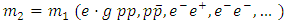
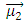 and charge
and charge 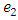 the equation ( in natural units) [1,2] is
the equation ( in natural units) [1,2] is 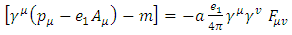
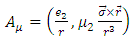 Or in the Hamiltonian form
Or in the Hamiltonian form 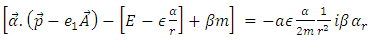
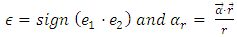 When
When 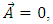 the above equation can be transformed to two- uncoupled second order Sturm-Liouville eigen value equations [1,15]; viz;
the above equation can be transformed to two- uncoupled second order Sturm-Liouville eigen value equations [1,15]; viz; 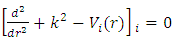
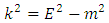 And the effective energy and angular momentum potential
And the effective energy and angular momentum potential 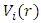 will have the same shape as shown in figure (2)Next one must include the dipole field
will have the same shape as shown in figure (2)Next one must include the dipole field  and the spin-spin terms due to the anomalous magnetic moment. In such case one obtains 4 -coupled first order equations [16].
and the spin-spin terms due to the anomalous magnetic moment. In such case one obtains 4 -coupled first order equations [16].
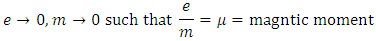 One gets an equation which is exactly solvable [14,15]; viz,
One gets an equation which is exactly solvable [14,15]; viz,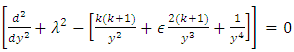
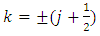 Also for a
Also for a  system, we have the Hamiltionian which includes the recoil and spin-spin terms
system, we have the Hamiltionian which includes the recoil and spin-spin terms 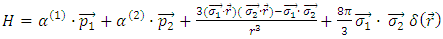
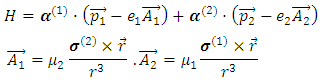
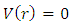
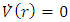
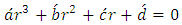
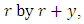 this can be transformed into
this can be transformed into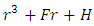
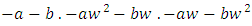
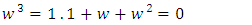
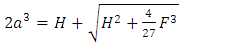
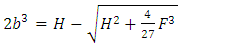
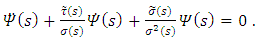
 and
and  are second-degree polynomials,
are second-degree polynomials,  is a first-degree polynomial and ψ(s) is a function of the hypergeometric-type.By taking
is a first-degree polynomial and ψ(s) is a function of the hypergeometric-type.By taking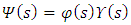
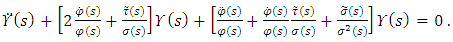
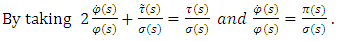
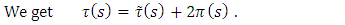
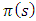 and
and 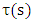 are polynomials of degree at most one.
are polynomials of degree at most one.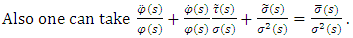
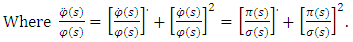
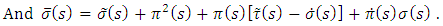
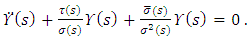
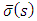 by
by 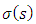 to obtain a constant
to obtain a constant 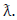 i.e.
i.e.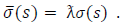
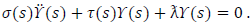
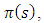 we get
we get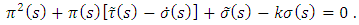

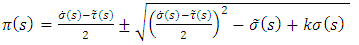
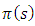 depend on the parameter
depend on the parameter 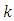 according to the plus and minus signs of
according to the plus and minus signs of 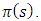 Since
Since 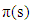 is a polynomial of degree at most one, so the expression under the square root must be the square of a polynomial. In this case, an equation of the quadratic form is available for the constant
is a polynomial of degree at most one, so the expression under the square root must be the square of a polynomial. In this case, an equation of the quadratic form is available for the constant 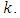 To determine the parameter
To determine the parameter 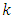 one must set the discriminant of this quadratic expression to be equal to zero. After determining the values of
one must set the discriminant of this quadratic expression to be equal to zero. After determining the values of 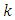 one can find the values
one can find the values 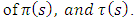 Applying the same systematic way for equation (28), we get
Applying the same systematic way for equation (28), we get 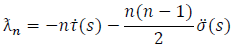
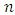 is the principle quantum number. By comparing equations (31) and (33), we get the energy eigenvalues equation.To get the eigenfunction
is the principle quantum number. By comparing equations (31) and (33), we get the energy eigenvalues equation.To get the eigenfunction 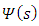 , one must know
, one must know 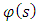 and
and 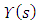 .We can obtian
.We can obtian 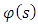 from equation (22).Now, we will obtian
from equation (22).Now, we will obtian 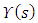 by
by 
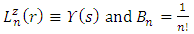
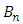 is a normalization constant and the weight function
is a normalization constant and the weight function 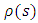 must satisfy the condition below
must satisfy the condition below 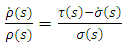
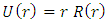 and subtituting in equation (1) [39-47], we get
and subtituting in equation (1) [39-47], we get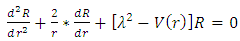
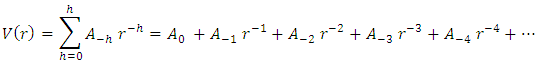
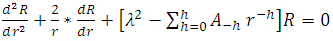
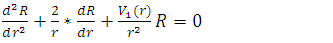
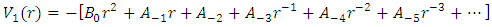
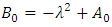 By substituting equation (41) in equation (40), we get
By substituting equation (41) in equation (40), we get 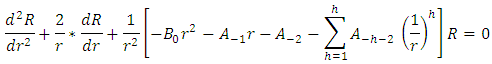
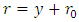 (where
(where  is the smallest distance from the origin to the particle) and take Maclurin expansion for the summation terms to the second order, one gets
is the smallest distance from the origin to the particle) and take Maclurin expansion for the summation terms to the second order, one gets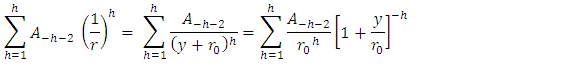
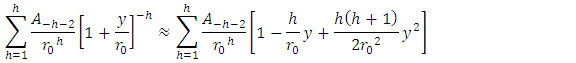
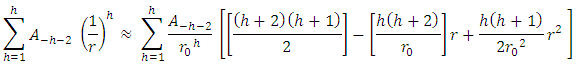
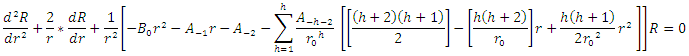

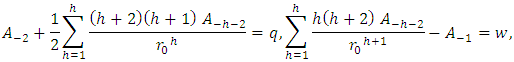
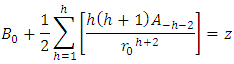 we obtain
we obtain 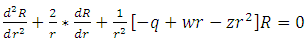
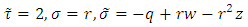 Equation (32) is used to obtain
Equation (32) is used to obtain 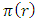
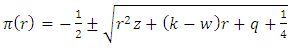
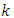
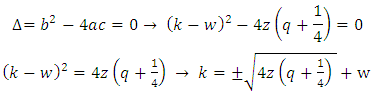
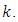 By substituting the values of
By substituting the values of 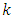 in equation (49) and take the negative value of
in equation (49) and take the negative value of 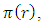 one gets
one gets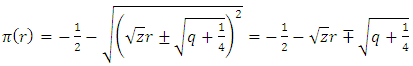
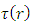
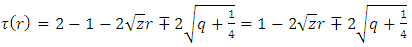
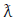
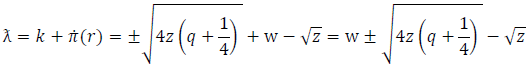
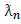 can be obtained from equation (33)
can be obtained from equation (33)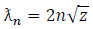

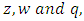 we get the energy eigenvalue equation for a general inverse polynomial potential
we get the energy eigenvalue equation for a general inverse polynomial potential  One can also calculate the eigenfunctions for the general inverse polynomial potential from equation (20) using the negative value of
One can also calculate the eigenfunctions for the general inverse polynomial potential from equation (20) using the negative value of  So first, we calculate
So first, we calculate  from equation (22)
from equation (22) 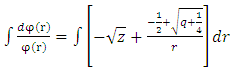

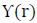 from equation (36) and equation (34)
from equation (36) and equation (34)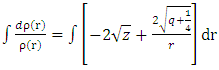
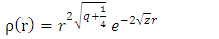
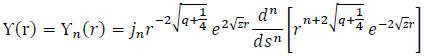
 is a normalization constant of
is a normalization constant of 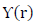 which can be expressed as an associated Laguerre polynomial, where
which can be expressed as an associated Laguerre polynomial, where 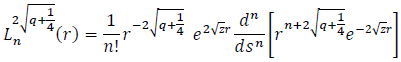
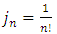 From equation (20), the eigenfunction becomes
From equation (20), the eigenfunction becomes 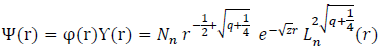
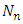 is a normalization constant of the eigenfunction
is a normalization constant of the eigenfunction 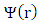 By substituting the values of
By substituting the values of 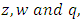 we get the eigenfunction for a general inverse polynomial potential
we get the eigenfunction for a general inverse polynomial potential Hence,
Hence,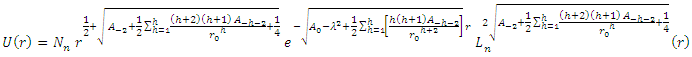 For the potential in equation (2)
For the potential in equation (2) 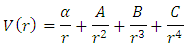 Where
Where 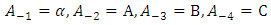 and the rest of the summation parameters in
and the rest of the summation parameters in  is equal to zeroThe energy eigenvalues become
is equal to zeroThe energy eigenvalues become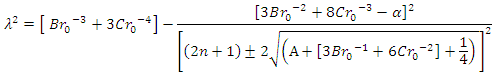 And, the state eigenfunctions are given as
And, the state eigenfunctions are given as 
 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML