Nishant Kumar Sharma
S.B.S P.G COLLEGE, RUDRAPUR, India
Correspondence to: Nishant Kumar Sharma, S.B.S P.G COLLEGE, RUDRAPUR, India.
| Email: |  |
Copyright © 2019 The Author(s). Published by Scientific & Academic Publishing.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/

Abstract
The theory of new type of particles called non-intractable particles, these are the particles which attend every mass state in universe, with it defining the statistic of Non-Intractable particles, the equations of Non-Interactive Mechanics, structure of Nucleus and Atom according to Non-Interactive Mechanics, proof of Dirac Particle-Antiparticle theory, Nishant Effect -The process by which Non-Interactive particles react with matter with this the proofs of Nishant effect 1. Linear harmonic oscillator 2. Plank’s radiation law 3. Mass- energy equivalence relation E=mc^2 4. velocity of light 5. The Relativistic relation E^2=P^2C^2+m^2c^4.
Keywords:
Ramanujan Entering, Ramanujan Effect, Velocity of Light
Cite this paper: Nishant Kumar Sharma, Non-Interactive Mechanics, Journal of Nuclear and Particle Physics, Vol. 9 No. 1, 2019, pp. 18-41. doi: 10.5923/j.jnpp.20190901.03.
1. Introduction
The Human Afford To Understand Physical Phenomena is Too Old, From Ancient Indian, Greek And So other Civilizations Put Their Approaches To Understand The Physical World Around Them Including Earth, Solar System, Galaxy And This Infinite Universe And So As The Modern Day Scientist Try to Find the Physical World’s nature, reason and properties around them such as Newton, A. Einstein.The Approach to understand the physical world is started with the assumption of the classic way by Newton, later Einstein and plank put their approaches to understand the advance form of physics in two different ways.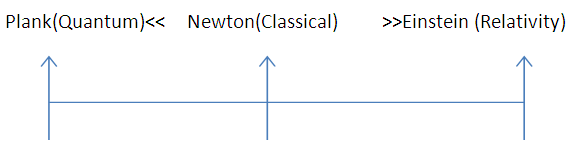 | Figure 1 |
Both ways of plank and Einstein is the another way to approach the way of Newton, both ways have their possibility in some special conditions. But still a question arise as all these three cases posses a same restriction. Now let’s see what is this restriction is-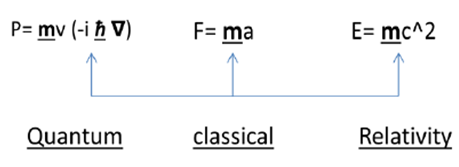 | Figure 2 |
The terms P(momentum), F(force), E(energy) is attached with the quantity m(mass) and it make possible to explain these quantities practically and physically, but still a question arise “How A Field Quanta Attend Mass”?. if any field’s quanta possessing these three nature of P(momentum), F(force), E(energy) then without the quantity m(mass) these quality can’t be explained so how a field quanta attend mass value the only understanding of mass of a quanta comes arrive when it comes in range of interaction of other quanta. 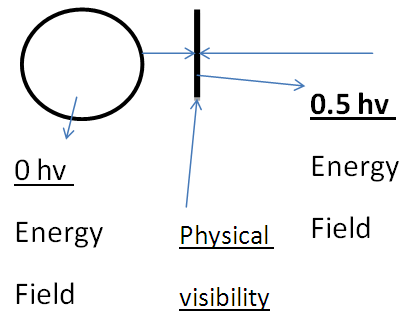 | Figure 3 |
Quantum mechanically a field quanta can be observed and explained at E=0.5hv Energy level that it’s “zero-point Energy.Here we introduce a new particles called “NON-INTERACTIBLE PARTICLES” or simply “N-I Particles” The field quanta of ‘0hv’ Energy level, the N-I particles are those particles, whose interaction with matter particles is negligible or they doesn’t exchange energy with energy or energy with mass when they interacts with matter obtained particles, they exchange energy with energy only when they interact with each other. Here by the term interaction means the energy exchange only occurs if the quantas are same or approximately similar energy level and interaction with other energy level quantas will be negligible.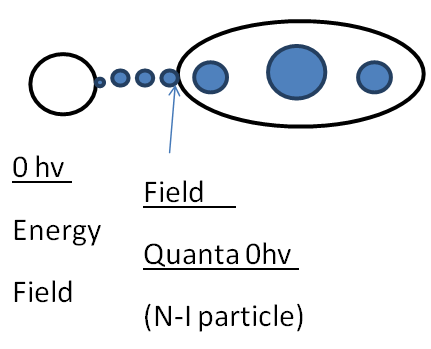 | Figure 4 |
Here in this above figure we can see that the interaction of N-i particles will occur when they attend the 0.5hv energy level. So now the approach to understand the mechanics of, how these non-intractable particles attend mass field? or simply the NON-INTERACTIVE MECHANICS.Now we examine what is this mechanics and how it works.
2. Statistical Formulation of Non-Interactive Mechanics
The assembly of these particles is known as ‘non-intractable particles’, by the term non-interactive means interaction of these particles with massed particles (field quantas of 0.5hv or higher energy levels) is very feeble or negligible and they only interchange energy when interact with each other, these particles approximately zero mass at both rest and movement but hold the ability to lead the mass and mass field in their app. zero mass level.So the basic points clear as :-1. These particles exchange energy during their collisions, without the interchange of mass or the exchanged mass quantity is very feeble.2. Particles posses the ability to follow spin as it provided by field’s geometry.3. Particles are indistinguishable, so there is no distinction between the various ways in which ni non-intractable particles are chosen, here the point to be notice that ‘these particles move only in straight line, and move without scattering with massed particles’, the reason is that these particles only interchange energy during their collision or interchanged mass quantity is very feeble so their effective collision is only with one axis and it’s components.Now we see the distribution law of ni non-intractable particles.A. DISTRIBUTION LAW:-Let there is ni particles present, the procedure of arranging these ni particles in gi cell’s.These particles obey ‘Pauli’s exclusion principle’ as they posses the spin of 1/2. so there is one particle or not any particle will present in a given cell, therefore the number of cells must be greater than number of particles gi >> ni.Here the “Non-intractable cell “means a place leave by a energy form ‘non-intractable particle’.Now if the primary particle obtain state in gi cell so the remaining cells will be (gi-1) !So the total number of different ways of arranging ni particles among gi states with energy level Ei is given by:-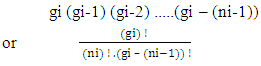 | (1) |
as (gi-ni) >>1 so (gi-ni+1)= (gi-ni)now for the case of non-interactive mechanics as mentioned earlier (gi>>ni) so the number of particles with respect to number of cells is very feeble, so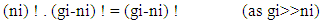 So the equation –(2) looks as:-
So the equation –(2) looks as:-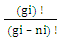 | (2) |
Now the point to be notice that these particles are indistinguishable, so the distribution law is given by:-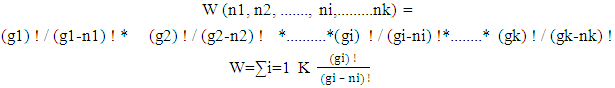 | (3) |
so this is the required distribution law for ni NON-INTERACTIBLE PARTICLES in gi non-intractable cells.B. MOST PROBABLE DISTRIBUTION:-Taking logarithm on the both sides of eq. –(3)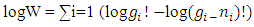 Now using stirling approximation:-Which is - log ni ! = ni log ni – ni
Now using stirling approximation:-Which is - log ni ! = ni log ni – ni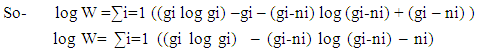 | (4) |
Here the point to be clear in above equation that both gi and ni varies, the reason of variation in gi is that the existence of Non-Intractable particles is beyond 0.5 hv energy levels, as described earlier at this range ‘A Non-intractable cell means a place leaved by a Non-intractable particle’. So here the cell will be the place which attained by 0hv energy level quanta, due to this in eq. -5 both ni and gi varies.Now differentiating eq.-(4)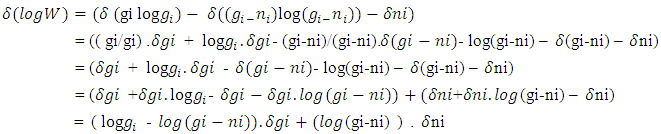 | (5) |
(i)- Conservation of total number of particles and cells, that number of particles and no. Of cells are always conserved.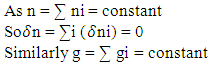
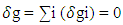 (ii) conservation of total Energy of system for particles and cells –
(ii) conservation of total Energy of system for particles and cells –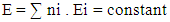
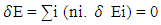 Similarly for gi
Similarly for gi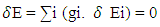 Substituting this in eq.-(6)
Substituting this in eq.-(6)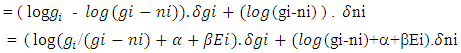 | (6) |
For solving this equation equating both term equals to zero and solving them sepretly:-FIRST PART -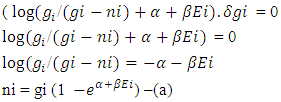 SECOND PART –
SECOND PART –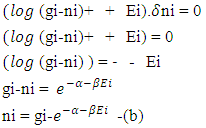 adding both eq. –a and –b substituting this in eq.-(7)
adding both eq. –a and –b substituting this in eq.-(7)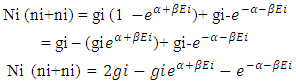 | (8) |
The above equation represents the way of cell distribution in Non-intractable particles as if Ni (ni+ni) = the number of non-intractable particles.2gi = the number of cells (2) available to non-intractable particles.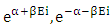 = geometries available to non-interactible particles.Now we discuss the behaviour of eq-(8) and process of cell distribution to non-interactible particles, as the existence of these particles is stated in 0hv energy level and the non-interactive mechanics deals with the mechanism of non-intractable particle from 0.hv energy level to 0.5hv energy level which can be stated as matter field, so in equation –(8) Ni represents the number of non-intractable particles, so as 2 non-intractable particle entered in matter field the 2 two cells (2gi) are provided to them, with two geometries of matter field
= geometries available to non-interactible particles.Now we discuss the behaviour of eq-(8) and process of cell distribution to non-interactible particles, as the existence of these particles is stated in 0hv energy level and the non-interactive mechanics deals with the mechanism of non-intractable particle from 0.hv energy level to 0.5hv energy level which can be stated as matter field, so in equation –(8) Ni represents the number of non-intractable particles, so as 2 non-intractable particle entered in matter field the 2 two cells (2gi) are provided to them, with two geometries of matter field 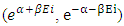 which are equal in amount but diffrent in direction, in which the geometry
which are equal in amount but diffrent in direction, in which the geometry 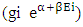 occupy a cell is stated as POSITIVE CURVE GEOMETRY, and the geometry which is equal in amount of positive curve geometry but cell less and oppositein direction is stated as NEGATIVE CURVE GEOMETY.So the points are clear as:-1. At the time of entering of a pair of non-intractable particle in the matter field, there will be two cells are provided to them.2. After the entering of these non-intractable particles in the matter field they comes under the two geometries in matter field (positive and negative curve geometries) which are equal in amount but opposite in direction
occupy a cell is stated as POSITIVE CURVE GEOMETRY, and the geometry which is equal in amount of positive curve geometry but cell less and oppositein direction is stated as NEGATIVE CURVE GEOMETY.So the points are clear as:-1. At the time of entering of a pair of non-intractable particle in the matter field, there will be two cells are provided to them.2. After the entering of these non-intractable particles in the matter field they comes under the two geometries in matter field (positive and negative curve geometries) which are equal in amount but opposite in direction 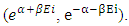 3. As one of the positive curve geometry
3. As one of the positive curve geometry 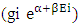 is cell occupied geometry, so the first particle enter in the matter field will follow the positive curve geometry, and with it equal in amount but opposite in direction geometry Negative curve geometry is also provided to non-intractable particle.So the prime rotation followed by non-intractable particles is under positive curve geometry or in other words right-handed rotation is the prime rotation followed by the Non-intractable particles,With it Negative curve geometry (left hand rotation) is also available to the Non-intractable particles which is just equal in amount but different in direction. C. POSITIVE AND NEGATIVE CURVE GEOMETRIESThe concept of curved space geometry is arise by the mathematician Riemann and then in general theory of relativity Einstein gives the description of curved space geometry, here in non-interactive mechanics, space geometry categorise by the different rotation properties of non-interactive particles in matter field.POSITIVE CURVE GEOMETRY-The term
is cell occupied geometry, so the first particle enter in the matter field will follow the positive curve geometry, and with it equal in amount but opposite in direction geometry Negative curve geometry is also provided to non-intractable particle.So the prime rotation followed by non-intractable particles is under positive curve geometry or in other words right-handed rotation is the prime rotation followed by the Non-intractable particles,With it Negative curve geometry (left hand rotation) is also available to the Non-intractable particles which is just equal in amount but different in direction. C. POSITIVE AND NEGATIVE CURVE GEOMETRIESThe concept of curved space geometry is arise by the mathematician Riemann and then in general theory of relativity Einstein gives the description of curved space geometry, here in non-interactive mechanics, space geometry categorise by the different rotation properties of non-interactive particles in matter field.POSITIVE CURVE GEOMETRY-The term 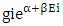 in eq. –(8) represents the positive curve geometry the name positive curve is due to positive signs of
in eq. –(8) represents the positive curve geometry the name positive curve is due to positive signs of 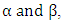 the geometry is a cell occupied positive curve geometry in which the rotation of N-I particles is right handed, rotation of proton in nucleus and all +1/2 (app.) rotating particles follow the positive curve geometry provided in matter field, the positive curve geometry can be explained as the rotation of planets around sun is the positive curve geometry. ‘So the prime rotating geometry is positive curve geometry in the matter field’ now as the cell occupied geometry so the interaction will occurs So “the cell occupied geometry in which the N-I particles follow the right handed rotation is called positive curve geometry”. NEGATIVE CURVE GEOMETRYThe term
the geometry is a cell occupied positive curve geometry in which the rotation of N-I particles is right handed, rotation of proton in nucleus and all +1/2 (app.) rotating particles follow the positive curve geometry provided in matter field, the positive curve geometry can be explained as the rotation of planets around sun is the positive curve geometry. ‘So the prime rotating geometry is positive curve geometry in the matter field’ now as the cell occupied geometry so the interaction will occurs So “the cell occupied geometry in which the N-I particles follow the right handed rotation is called positive curve geometry”. NEGATIVE CURVE GEOMETRYThe term 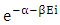 in eq.-(8) represents the negative curve geometry, the name negative curve is due to the negative sign of
in eq.-(8) represents the negative curve geometry, the name negative curve is due to the negative sign of 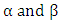 .the geometry is a non cell ocuupied geometry, which is equal in amount to positive curve geometry but diffrent in rotation. D. NON-INTERACTIBLE PARTICLES ENTERING IN MATTER FIELD AND IT’S EXPLANATIONNow we see the equation of entering of non-intractable particles in matter field, this can be seen as the entering of 0hv energy field quanta (N-I particle) in 0.5hv energy field quanta or in intractable matter field.The eq. –(8) represents the distribution of ni Non-intractable particles in gi cell’s which is
.the geometry is a non cell ocuupied geometry, which is equal in amount to positive curve geometry but diffrent in rotation. D. NON-INTERACTIBLE PARTICLES ENTERING IN MATTER FIELD AND IT’S EXPLANATIONNow we see the equation of entering of non-intractable particles in matter field, this can be seen as the entering of 0hv energy field quanta (N-I particle) in 0.5hv energy field quanta or in intractable matter field.The eq. –(8) represents the distribution of ni Non-intractable particles in gi cell’s which is 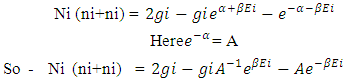 | (8) |
It is convenient to consider continuous distribution of particles energies rather than discrete energies such as- E1, E2, E3........EK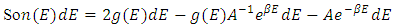 | (9) |
Let us assume n(E) represents the number of particles having energies between E and E+dE if P is the Momentum of given particles so:- 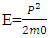 But as we know that particles posses almost zero mass in both rest and moving, so as
But as we know that particles posses almost zero mass in both rest and moving, so as 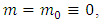 now here
now here 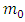 is the approximately equal to zero mass value so-
is the approximately equal to zero mass value so- 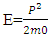 (where m0 is the mass of non-interactible particle approximately equal to zero)so the eq.- (10) transform into:-
(where m0 is the mass of non-interactible particle approximately equal to zero)so the eq.- (10) transform into:-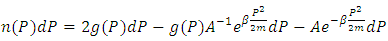 | (10) |
Here n(P) represents the no. Of non-intractable particles having momentum between P and P+dP.Then priori probability g(p) that a particle have momentum between P and P+dP is equal to be number of cell’s in the phase space within, which such a particle may exist.As mentioned earlier these particles move only in straight line so:-g(P) dP= volume of the zone in the phase space / volume of one cellzone of Non-intractable particles in phase space is given by only a single position and momentum co-ordinates, as we know that these particles could travel only in one directions,” so the volume of zone in phase space is given by 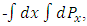 while the volume of one cell is
while the volume of one cell is 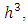 so the point is cleared here that particles have six-dimensional space or may be more to move, but they bound to move in the dimensional space where x is position coordinate and Px is relative momentum, as we choose x and Px axis to move :-
so the point is cleared here that particles have six-dimensional space or may be more to move, but they bound to move in the dimensional space where x is position coordinate and Px is relative momentum, as we choose x and Px axis to move :-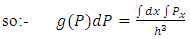 | (11) |
here non-intractable particles have x,y,z axis and their relative momentum 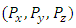 to move but they are bound to move only in straight lineHere
to move but they are bound to move only in straight lineHere 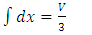 because
because 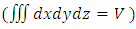 As we know that particle lying in the momentum range between Px and Px+dPx (as six dimensional space x,Px,yPy and z,Pz available but particle bound to move in the straight line) so:-
As we know that particle lying in the momentum range between Px and Px+dPx (as six dimensional space x,Px,yPy and z,Pz available but particle bound to move in the straight line) so:- 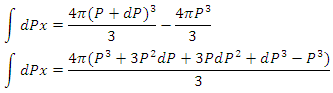
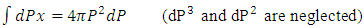
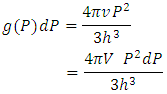 Substituting above value of g(P) dP in equation-(11)
Substituting above value of g(P) dP in equation-(11)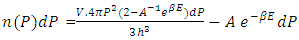 Since the total number of non-intractable particles is N so-
Since the total number of non-intractable particles is N so-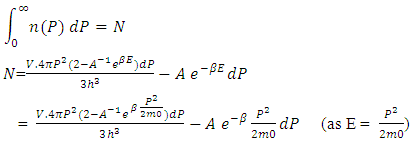 So:-
So:-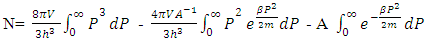 Neglecting the first integral on R.H.S due to integral limits
Neglecting the first integral on R.H.S due to integral limits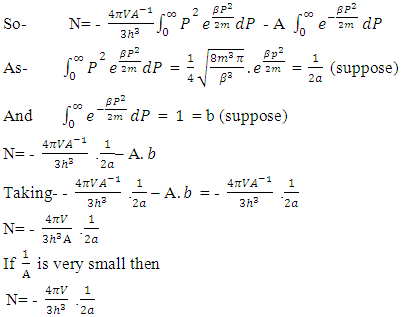 | (12) |
Now above mentioned equation can be solved in two parts, let’s see them-1. The first solution of equation –(12) 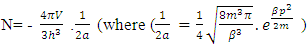
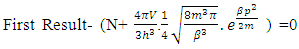 | (13a) |
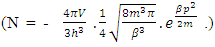 | (13b) |
1. Second solution of equation –(13) have two forms, the equation –(13) is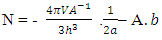 -(12) if the value of
-(12) if the value of 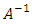 is small then
is small then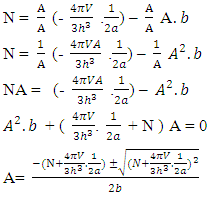 | (14) |
If A=0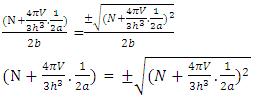 As
As 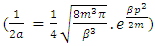 so above mentioned equation turned into-
so above mentioned equation turned into-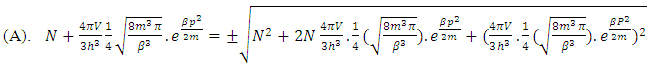 | (15) |
This is the first form of the second solution of the equation –(12)(B). This is the second form of the second solution of equation –(12) 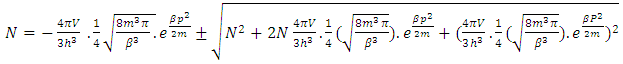 | (16) |
The above mentioned equation is the Non-intractable (N-I) Particle Entering equation in the Matter field equation.Here the meaning represented by the each term in give equation is 1. N=Non-intractable Particle (N-I particle).2. 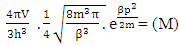 The Matter provided at the time of Entering of N-I Particles.3.
The Matter provided at the time of Entering of N-I Particles.3. 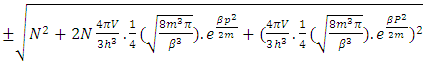 = Distribution of N-I particles and Matter field or simply Process of Formation (f p.o.f).The four equations of non-interactive mechanics are
= Distribution of N-I particles and Matter field or simply Process of Formation (f p.o.f).The four equations of non-interactive mechanics are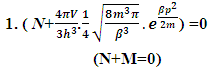 (13a)Here N is (N-I particle) while M is mass field, so the ‘ sum of non-intractable particle and matter field is equal to class zero particle field’. In other word ‘A field quantais the union of non-intractable particle and matter field ’.
(13a)Here N is (N-I particle) while M is mass field, so the ‘ sum of non-intractable particle and matter field is equal to class zero particle field’. In other word ‘A field quantais the union of non-intractable particle and matter field ’.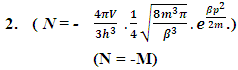 (13b)The equation showing that ‘the non-intractable particle is equal to disintegrated matter’. here the term –M showing the disintegrated matter .
(13b)The equation showing that ‘the non-intractable particle is equal to disintegrated matter’. here the term –M showing the disintegrated matter . 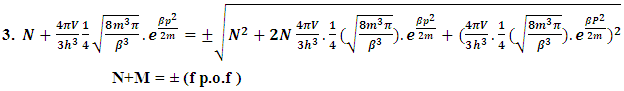 (15)The above shown equation showing that ‘union of N-I particle and matter field is equal to process of formation ’. Now if we equate equation -1 and -3 than we find 1. (N+M=0) 3. N+M = ± (f p.o.f ) 0 = ± (f p.o.f ) so the process of formation is equal to class zero particle .
(15)The above shown equation showing that ‘union of N-I particle and matter field is equal to process of formation ’. Now if we equate equation -1 and -3 than we find 1. (N+M=0) 3. N+M = ± (f p.o.f ) 0 = ± (f p.o.f ) so the process of formation is equal to class zero particle . 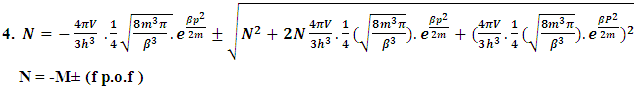 (16)The above shown equation showing that ‘N-I particle is equal to sum of disintegrated matter and the process of formation ‘ . this equation is the N-I particles entering equation in matter field.THIS VALUE IS EQUALS TO THE MESONIC X-RAY OF NUCLEUS RADIUS 1.2+_0.03 fm.This is also same as deuterons binding energy 2.225+_0.002 MevNow let’s see a another case if (N = -M± (f p.o.f) and 0 =± (f p.o.f)So N = -M + 0 The N-I particles are indistinguishable so taking 0 = N + M’ the N-I particle is indistinguishable but theirs variation in matter as they posses interaction property so
(16)The above shown equation showing that ‘N-I particle is equal to sum of disintegrated matter and the process of formation ‘ . this equation is the N-I particles entering equation in matter field.THIS VALUE IS EQUALS TO THE MESONIC X-RAY OF NUCLEUS RADIUS 1.2+_0.03 fm.This is also same as deuterons binding energy 2.225+_0.002 MevNow let’s see a another case if (N = -M± (f p.o.f) and 0 =± (f p.o.f)So N = -M + 0 The N-I particles are indistinguishable so taking 0 = N + M’ the N-I particle is indistinguishable but theirs variation in matter as they posses interaction property so 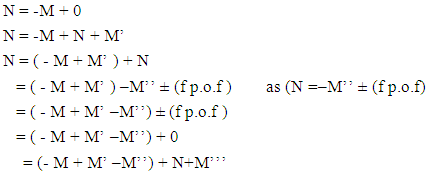 And so as further again this shows the continuous extension of the procedure as this also states that a N-I particle posses the infinite expansion property this states that the process of Non-interactive mechanics is a continues and periodic system in which matter field always extend by every step. Here the meaning represented by the each term in give equation is 1. N=Non-intractable Particle (N-I particle).2.
And so as further again this shows the continuous extension of the procedure as this also states that a N-I particle posses the infinite expansion property this states that the process of Non-interactive mechanics is a continues and periodic system in which matter field always extend by every step. Here the meaning represented by the each term in give equation is 1. N=Non-intractable Particle (N-I particle).2. 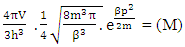 The Matter provided at the time of Entering of N-I Particles.3.
The Matter provided at the time of Entering of N-I Particles.3. 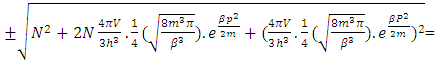 Distribution of N-I particles and Matter field or simply Process of Formation (f p.o.f).Now let’s examine the above equations the each term:-1. ‘N’ the Non-intractable particle- In above mentioned equations the term ‘N’ represents the Non-intractable particle. this term shows varies types of quality in matter field and out of matter field which are.A. Ramanujan Entering.B. Ramanujan Effect.A. Ramanujan Entering:- In above mentioned equations the term N represents the N-I particle, whose interaction with matter field is negligible, so for the matter field particle it become a ideal particle so, mathematically-
Distribution of N-I particles and Matter field or simply Process of Formation (f p.o.f).Now let’s examine the above equations the each term:-1. ‘N’ the Non-intractable particle- In above mentioned equations the term ‘N’ represents the Non-intractable particle. this term shows varies types of quality in matter field and out of matter field which are.A. Ramanujan Entering.B. Ramanujan Effect.A. Ramanujan Entering:- In above mentioned equations the term N represents the N-I particle, whose interaction with matter field is negligible, so for the matter field particle it become a ideal particle so, mathematically-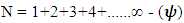 this equation represents that the sum of infinite matter field particle is equal to non-interactible particle.Now multiplying equation
this equation represents that the sum of infinite matter field particle is equal to non-interactible particle.Now multiplying equation 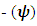 by 4 on both sides then:-
by 4 on both sides then:-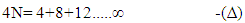 Now substracting equation -(∆) from - (𝝍) we get-
Now substracting equation -(∆) from - (𝝍) we get-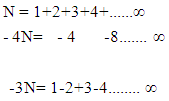 This gives-
This gives-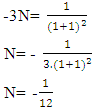 | (17) |
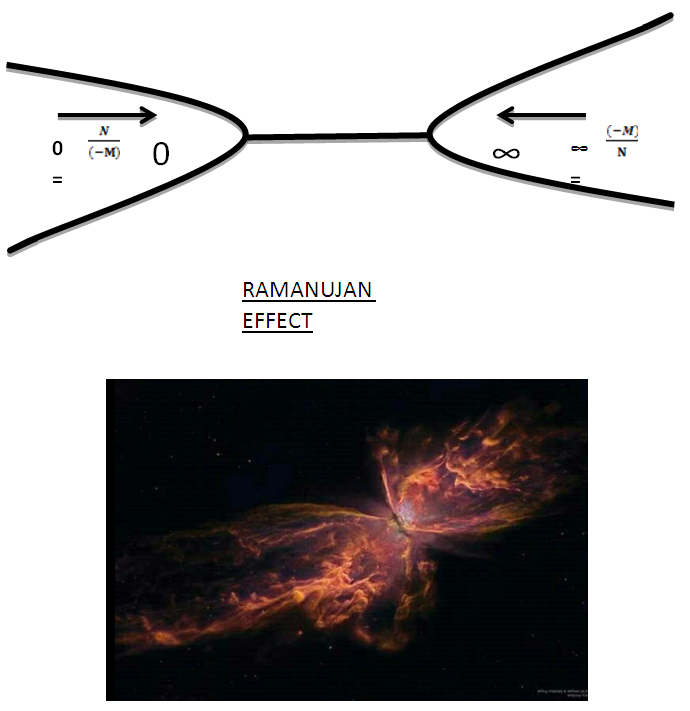
The relation is derived by Indian mathematician “Srinivasan Ramanujan”.Here in equation 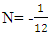 The given terms can be written as 12N = -1 so by the L.H.S and R.H.S we Can see that the 12 Non Intractable particles emits by Field quanta in the direction of positive curve geometry till the condition of 12N arrives and one Non –Intractable particle emits in the direction of Negative curve geometry. After completing the procedure 12N = -1 Matter field is available to Positive curve geometry following Non-Intractable Particles.From this point they have mass field and it’s relative state to attain the mass value provided in field.As the mathematical relation is given by “shri – srinivasn ramanujan”. So the entering of 12 non-intractable particles in mass field by following positive curve geometry while one N-i Particle is following Negative curve Geometry is called as ‘Ramanujan Entering’.
The given terms can be written as 12N = -1 so by the L.H.S and R.H.S we Can see that the 12 Non Intractable particles emits by Field quanta in the direction of positive curve geometry till the condition of 12N arrives and one Non –Intractable particle emits in the direction of Negative curve geometry. After completing the procedure 12N = -1 Matter field is available to Positive curve geometry following Non-Intractable Particles.From this point they have mass field and it’s relative state to attain the mass value provided in field.As the mathematical relation is given by “shri – srinivasn ramanujan”. So the entering of 12 non-intractable particles in mass field by following positive curve geometry while one N-i Particle is following Negative curve Geometry is called as ‘Ramanujan Entering’.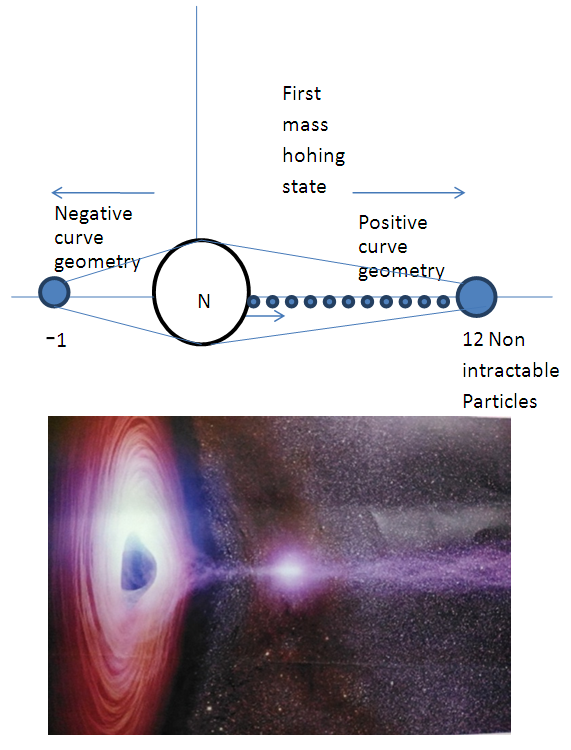 (image- NASA)Similar entering procedure observed by NASA when a particle comes out from black hole.This is similar to the theoretical and mathematical results mentioned in ‘Ramanujan Entering’.B. Ramanujan Effect-In Ramanujan effect we will study the exchange process of Non-intractable particles.so Equation -14(a) and equation –14(b) are
(image- NASA)Similar entering procedure observed by NASA when a particle comes out from black hole.This is similar to the theoretical and mathematical results mentioned in ‘Ramanujan Entering’.B. Ramanujan Effect-In Ramanujan effect we will study the exchange process of Non-intractable particles.so Equation -14(a) and equation –14(b) are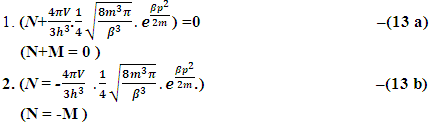 Here
Here 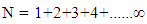 which gives ‘
which gives ‘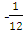 ‘ after solution, so here N is equal to app. infinite number of positive curve geometry particle so the above relation can be written as
‘ after solution, so here N is equal to app. infinite number of positive curve geometry particle so the above relation can be written as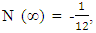 here infinite positive curve geometry particles are the function of Non-intractable Particle. Now taking equation –(13 b)
here infinite positive curve geometry particles are the function of Non-intractable Particle. Now taking equation –(13 b)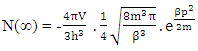 Now multiplying
Now multiplying 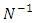 on the left of both sides we get
on the left of both sides we get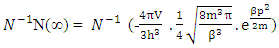 This gives-
This gives-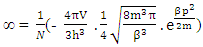
 -equation (i)Also -
-equation (i)Also - 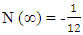 multiplying
multiplying 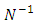 on the left of both sides we get
on the left of both sides we get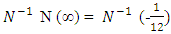
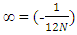
 -equation (ii)Also-
-equation (ii)Also- 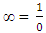
 -equation (iii)This gives -For ∞ this gives the relation
-equation (iii)This gives -For ∞ this gives the relation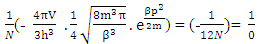
 equation-(18)Now again –(13 b)
equation-(18)Now again –(13 b)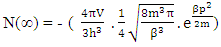 here N is Non-intractable particle , and ∞ represents the infinite number of positive curve geometry particles which are the function of N-I particle.Now taking inverse of above equation –(13 b)
here N is Non-intractable particle , and ∞ represents the infinite number of positive curve geometry particles which are the function of N-I particle.Now taking inverse of above equation –(13 b)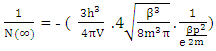 Multiplying by N on both sides of given equation
Multiplying by N on both sides of given equation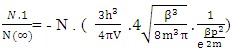 Now multiplying
Now multiplying 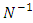 on numerator and denominator both this gives-
on numerator and denominator both this gives-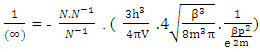 Which gives-
Which gives-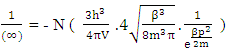
 -equation (j)As
-equation (j)As 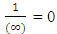 So -
So - 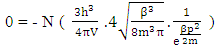
 -equation (jj)Also-
-equation (jj)Also- 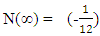 Taking inverse on both sides we get-
Taking inverse on both sides we get-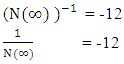 Multiplying
Multiplying 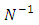 on the denomenator of both sidesFirst the equation can be written as
on the denomenator of both sidesFirst the equation can be written as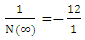 Now
Now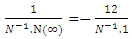 Which gives
Which gives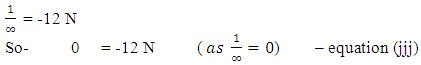 Now examining the above equations (i) and (jj) are-
Now examining the above equations (i) and (jj) are-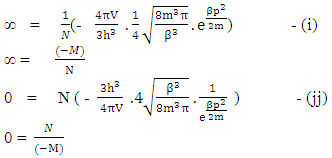 The above shown equations shows that from equation -14(a) and -14(b)1. N+M=0, 2. N= -MThe union or sum of element and matter creates a field quanta and as disintegration of matter occurs after that this disintegrate matter collide with field quanta which creates two views or phenomena which are –when
The above shown equations shows that from equation -14(a) and -14(b)1. N+M=0, 2. N= -MThe union or sum of element and matter creates a field quanta and as disintegration of matter occurs after that this disintegrate matter collide with field quanta which creates two views or phenomena which are –when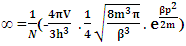
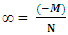 (here N is non-interactible particle and -M is disintegrate mass)From this view all the mechanism is seems as ∞, in other words in this view disintegrated matter is always increase with every step.So as
(here N is non-interactible particle and -M is disintegrate mass)From this view all the mechanism is seems as ∞, in other words in this view disintegrated matter is always increase with every step.So as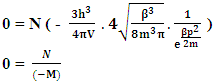 From this view all the mechanism is seems as 0, in other words in this view field quantas continuously emits.So “The Non-intractable Particle and matter creates field quantas, this creates two views of same phenomenaIn which one view represents view of ∞ (the view where matter continuously disintegrates)and one view shows the view of zero 0(where field quantas continuously emit ) by both of these view field quantas and matter fields exchange by each other views, This is ‘Ramanujan effect’ for disintegrate matter and N-I Particle”.
From this view all the mechanism is seems as 0, in other words in this view field quantas continuously emits.So “The Non-intractable Particle and matter creates field quantas, this creates two views of same phenomenaIn which one view represents view of ∞ (the view where matter continuously disintegrates)and one view shows the view of zero 0(where field quantas continuously emit ) by both of these view field quantas and matter fields exchange by each other views, This is ‘Ramanujan effect’ for disintegrate matter and N-I Particle”.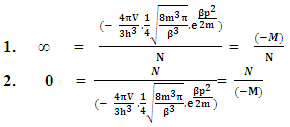
 3. The Interaction of Non-Intractable Particles with Matter (M)- The mass term (M) in above equations shown as –
3. The Interaction of Non-Intractable Particles with Matter (M)- The mass term (M) in above equations shown as –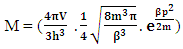 For the disintegrated matter the term also appear as –
For the disintegrated matter the term also appear as –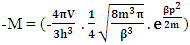 By equation -14(a) and -14(b) we see that-
By equation -14(a) and -14(b) we see that- The sum of N-I particle and Matter creates field quanta and by equation -14(b) the non-intractable particle is equal to disintegrated matter. The qualities of this mass (M) field are-As N-i particle follow ramanujan entering procedure by following the relation 12 N = -1, this equation states that 12 Positive curve geometry following particle is equal to the negative curve geometry following one N-I particle, so at this point positive curve geometry and the relative mass of the field is also available for N-I Particle.“After entering in the Matter field the N-I particle is surrounded by the region of
The sum of N-I particle and Matter creates field quanta and by equation -14(b) the non-intractable particle is equal to disintegrated matter. The qualities of this mass (M) field are-As N-i particle follow ramanujan entering procedure by following the relation 12 N = -1, this equation states that 12 Positive curve geometry following particle is equal to the negative curve geometry following one N-I particle, so at this point positive curve geometry and the relative mass of the field is also available for N-I Particle.“After entering in the Matter field the N-I particle is surrounded by the region of 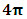 which posses the volume of
which posses the volume of 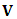
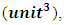 here in this region the 3 types of mass attending method is available to each N-I particle, each method posses the degree of freedom of
here in this region the 3 types of mass attending method is available to each N-I particle, each method posses the degree of freedom of 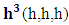 this state of N-I Particle is known as ‘ 3-Gate Body’, so the region of
this state of N-I Particle is known as ‘ 3-Gate Body’, so the region of 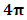 with volume of
with volume of 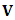
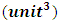 with ‘ 3-Gate Body’ in which each posses degree of freedom of
with ‘ 3-Gate Body’ in which each posses degree of freedom of 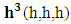 is available to N-I particle.After attending 3-Gate body N-I particle is ready to attend the mass of field. now the mass potential is
is available to N-I particle.After attending 3-Gate body N-I particle is ready to attend the mass of field. now the mass potential is 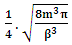 here this term is seems as fourth part of mass potential, so each mass field posses 4- mass potential, This potentials are named as “Mass-Particle Directors” Or simply ‘M-P Directors’, here each M-P director posses the region of
here this term is seems as fourth part of mass potential, so each mass field posses 4- mass potential, This potentials are named as “Mass-Particle Directors” Or simply ‘M-P Directors’, here each M-P director posses the region of 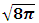 and the mass value of
and the mass value of 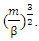 so after attending ‘9-Gate Body’ and “4-Mass-Particle Directors” N-I Particle start to gain the mass of the field.
so after attending ‘9-Gate Body’ and “4-Mass-Particle Directors” N-I Particle start to gain the mass of the field.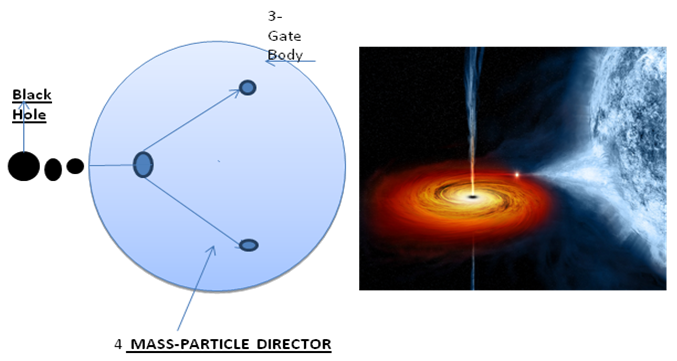 The image of this particle is captured by NASA.The term
The image of this particle is captured by NASA.The term 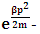 This exponential term is mentioned in two forms
This exponential term is mentioned in two forms 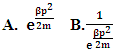 The part A gives the view of ∞ (to gain Matter field) due to this N-I particle seems to expand exponentially with the expansion rate of
The part A gives the view of ∞ (to gain Matter field) due to this N-I particle seems to expand exponentially with the expansion rate of 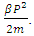 The part B gives the view of 0, from this view only the Non-intractable particles expand and joint with other N-I particles with The rate of
The part B gives the view of 0, from this view only the Non-intractable particles expand and joint with other N-I particles with The rate of 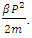
3. The Process of Formation and Mass Distribution
so after getting 9-gate body and expansion N-I particle attend the mass field, as getting the mass interactive matter form now the distribution of energy takes place in N-I Particles so by equation-(17)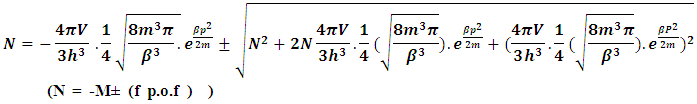 (17)Here the part-
(17)Here the part-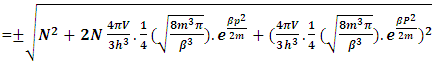 is described as process of formationOr simply f(p.o.f), now opening this above equation-
is described as process of formationOr simply f(p.o.f), now opening this above equation- 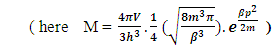
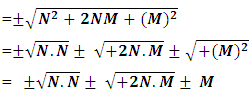 | (19) |
Now by equation-(8)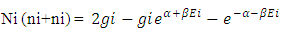 two cells are provided to every N-I particle as where the first cell holding particle is positive curve geometry particle and will follow right hand rotation while negative curve geometry is also available in the field, so as by equation-(19) we can see two sign variations are available in above equation-(19) Which are
two cells are provided to every N-I particle as where the first cell holding particle is positive curve geometry particle and will follow right hand rotation while negative curve geometry is also available in the field, so as by equation-(19) we can see two sign variations are available in above equation-(19) Which are 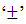 neutral field cell,‘+’ positive field cell so equation –(19) states that two N-I particles
neutral field cell,‘+’ positive field cell so equation –(19) states that two N-I particles 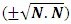 are entering from 0 energy field, then these two particles entering in the matter field
are entering from 0 energy field, then these two particles entering in the matter field 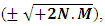 this matter field is ‘dense energy field’
this matter field is ‘dense energy field’ 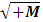 and positive curve geometry field but as the cell distribution formula states as their’s one cell for positive curve geometry particle while other cell is for neutral field particle, so one N-I particle will stay in this field and obtain the relative field’s mass this positive curved geometry’s cell occupied stable and right-hand rotating particle is ‘PROTON’. while the second N-I particle will also enter in this ‘dense energy field ‘ (as equation stating that
and positive curve geometry field but as the cell distribution formula states as their’s one cell for positive curve geometry particle while other cell is for neutral field particle, so one N-I particle will stay in this field and obtain the relative field’s mass this positive curved geometry’s cell occupied stable and right-hand rotating particle is ‘PROTON’. while the second N-I particle will also enter in this ‘dense energy field ‘ (as equation stating that 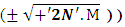 but the only cell ispresent in this field is occupied so this second N-I particle will collect some mass from positively curved dense energy field and transmit to the ‘spread energy field
but the only cell ispresent in this field is occupied so this second N-I particle will collect some mass from positively curved dense energy field and transmit to the ‘spread energy field 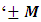 and as cell distribution formula this spread enrgy field is under meutral field particle and follow negative curve geometry this spread energy field particle, which is left-handed rotating and following negative curve geometry and also unstable in dense energy field and positive curve geometry is ‘ELECTRON’.4. NUCLEUS AND ATOM THE MOST STABLE STATEThe points are clear by non-intractable mechanics are-1. 2 cells are provided to non-intractable particles, in which one is for positive curve geometry particle, while another one is not filled by another non-intractable particle.2. As negative curve geometry is cell less so this cell can’t be filled by not the positive curve geometry particle neither negative curve geometry particle, so this is the second cell will be filled by the neutral particle (+,0,-).3. energy of field is distributed in two parts - 1. Dense energy field 2. Spread energy field.4. two types of field geometry is provided which are-i. positive curve geometry .ii. negative curve geometry.5. the geometries are divide into four parts in which first part isi. pure positive curve geometry and maintained positive curve geometry.ii. pure negative geometry and maintained negative curve geometry.6. (i) pure positive curve geometry is controlled by it’s cell holding particle
and as cell distribution formula this spread enrgy field is under meutral field particle and follow negative curve geometry this spread energy field particle, which is left-handed rotating and following negative curve geometry and also unstable in dense energy field and positive curve geometry is ‘ELECTRON’.4. NUCLEUS AND ATOM THE MOST STABLE STATEThe points are clear by non-intractable mechanics are-1. 2 cells are provided to non-intractable particles, in which one is for positive curve geometry particle, while another one is not filled by another non-intractable particle.2. As negative curve geometry is cell less so this cell can’t be filled by not the positive curve geometry particle neither negative curve geometry particle, so this is the second cell will be filled by the neutral particle (+,0,-).3. energy of field is distributed in two parts - 1. Dense energy field 2. Spread energy field.4. two types of field geometry is provided which are-i. positive curve geometry .ii. negative curve geometry.5. the geometries are divide into four parts in which first part isi. pure positive curve geometry and maintained positive curve geometry.ii. pure negative geometry and maintained negative curve geometry.6. (i) pure positive curve geometry is controlled by it’s cell holding particle 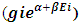 (ii). All three geometries are controlled by neutral cell occupied particle.So the figure according to these details is –
(ii). All three geometries are controlled by neutral cell occupied particle.So the figure according to these details is –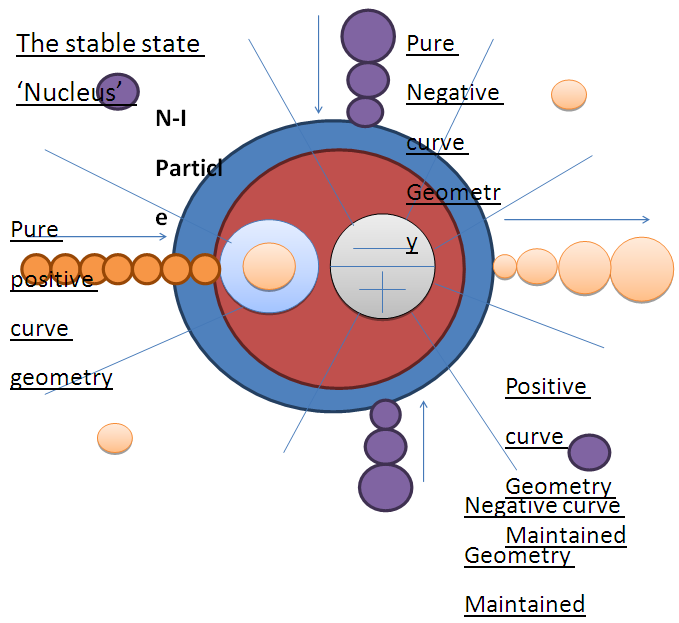 This is the figure of stable state’ nucleus and atom.
This is the figure of stable state’ nucleus and atom. This is the LIGO Experiment BY which Gravitational waves was detected shows same structure as above structure of Nucleus and atom according to Non-Interactive Mechanics.
This is the LIGO Experiment BY which Gravitational waves was detected shows same structure as above structure of Nucleus and atom according to Non-Interactive Mechanics.
4. NISHANT Effect
Process for Non-Intractable Particles to attend and react with matter(i). if we look a reaction is started by interactions, then according to particle-antiparticle theory both are conserved in any possible reaction.(ii). then according to this how can a reaction be possible, because every ‘+Ve’ particle is opposed by it’s ‘-Ve’ antiparticle, and due to this it will be almost impossible to perform any possible reaction, we can understand it according to numbers-(.......... -3,-2,-1,+1,+2,+3 ............)As all the numbers are equal in amount but opposite in nature due to it in any possible reaction they will cross the impact of each other.(iii). Here if the distribution of matter is equal in both sides ( ‘-Ve’, ‘+Ve’ ) then after the collision during in any reaction all the amount of matter will be destroyed due to this there will be no chance other possible new reactions to happen.(iv). The only way when a reaction is possible is possible when the reaction type is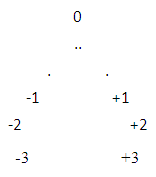 A neutral field is required for the production of any reaction, thus any reaction when collision occurs the reaction will be stable.(v). According to the non-interactive mechanics cell distribution formula.
A neutral field is required for the production of any reaction, thus any reaction when collision occurs the reaction will be stable.(v). According to the non-interactive mechanics cell distribution formula.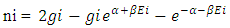 in this equation two cells are provided and positive cure geometry is prime and a cell occupied geometry, so in this case ‘Number of particles is always greater than number of Anti-particles’, as according to the non-interactive mechanics first particle enter in the matter field is goes under positive curve geometry and R.H rotating particle.So due to this point the number figure will be
in this equation two cells are provided and positive cure geometry is prime and a cell occupied geometry, so in this case ‘Number of particles is always greater than number of Anti-particles’, as according to the non-interactive mechanics first particle enter in the matter field is goes under positive curve geometry and R.H rotating particle.So due to this point the number figure will be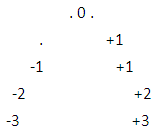 The number of particles is near to neutral field rather than Anti-particles.Non-Interactive mechanics four equations-
The number of particles is near to neutral field rather than Anti-particles.Non-Interactive mechanics four equations-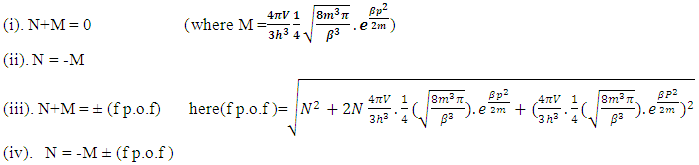 Now from equation (iv)N = -M ± (f p.o.f)So N = -M + 0The N-I particles are indistinguishable so taking 0 = N + M’ the N-I particle is indistinguishable but theirs variation in matter as they posses interaction property so
Now from equation (iv)N = -M ± (f p.o.f)So N = -M + 0The N-I particles are indistinguishable so taking 0 = N + M’ the N-I particle is indistinguishable but theirs variation in matter as they posses interaction property so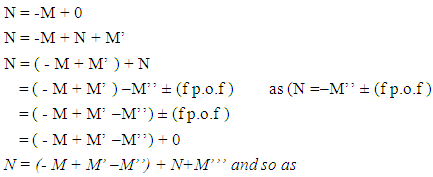 “Matter field is continuously increasing after the production of non-intractable particles”.‘In case of non-intractable particle the positive curve geometry’s matter always increase by the production of new non-intractable particle, with respect to negative curve geometry’s matter.(vii). So the required steps are-As mentioned in non-interactive mechanics the two geometries are (i). Positive Curve Geometry, (ii). Negative Curve GeometryThe positive geometry is possessing 12 mass holding states while negative is possessing 11 mass leaving states –Where these mass leaving states posses cell less geometry, so in that condition negative curve geometry continuously proceed till the Non-intractable particle emit, here the available matter field quality is tri nature.3.2 NISHANT EFFECT- “ANY REACTION OR PHENOMENA IS CAN’T BE POSSIBLE TILL MATTER FIELD DOESN’T FOLLOW TRI-NATURE PROPERTY AND NEGATIVE CURVE GEOMETRY AND NOT ANY N-I PARTICLES ENTER IN THE POSITIVE CURVE GEOMETRY’S MAXIMUM EXCITING STATE. WHERE THE NUMBER OF PARTICLES IS ALWAYS GREATER THAN IT’S RELATIVE ANTI-PARTICLES, AND BY PRODUCTION OF THESE NON-INTRACTABLE PARTICLE MATTER FIELD ALWAYS INCREASE”.3.3 EQUATIONS AND PROOFS (Spark Chamber Photos)-(i). The total energy of a reaction is given by-
“Matter field is continuously increasing after the production of non-intractable particles”.‘In case of non-intractable particle the positive curve geometry’s matter always increase by the production of new non-intractable particle, with respect to negative curve geometry’s matter.(vii). So the required steps are-As mentioned in non-interactive mechanics the two geometries are (i). Positive Curve Geometry, (ii). Negative Curve GeometryThe positive geometry is possessing 12 mass holding states while negative is possessing 11 mass leaving states –Where these mass leaving states posses cell less geometry, so in that condition negative curve geometry continuously proceed till the Non-intractable particle emit, here the available matter field quality is tri nature.3.2 NISHANT EFFECT- “ANY REACTION OR PHENOMENA IS CAN’T BE POSSIBLE TILL MATTER FIELD DOESN’T FOLLOW TRI-NATURE PROPERTY AND NEGATIVE CURVE GEOMETRY AND NOT ANY N-I PARTICLES ENTER IN THE POSITIVE CURVE GEOMETRY’S MAXIMUM EXCITING STATE. WHERE THE NUMBER OF PARTICLES IS ALWAYS GREATER THAN IT’S RELATIVE ANTI-PARTICLES, AND BY PRODUCTION OF THESE NON-INTRACTABLE PARTICLE MATTER FIELD ALWAYS INCREASE”.3.3 EQUATIONS AND PROOFS (Spark Chamber Photos)-(i). The total energy of a reaction is given by-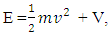 here E is total energy of a reaction
here E is total energy of a reaction 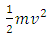 is kinetic energy and V is potential energy(ii). Now the system where photonic decays are is proceeding the kinetic energy of that phenomena is represented as
is kinetic energy and V is potential energy(ii). Now the system where photonic decays are is proceeding the kinetic energy of that phenomena is represented as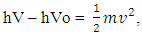 here hV is the energy (E) of a system while hVo is work function and
here hV is the energy (E) of a system while hVo is work function and 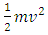 is kinetic energy of the system.If the matter is following try-nature property than dividing the frequency of E = hV in three parts.
is kinetic energy of the system.If the matter is following try-nature property than dividing the frequency of E = hV in three parts. Arranging these in equation of (ii)-
Arranging these in equation of (ii)-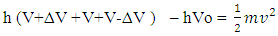
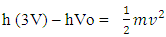
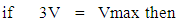
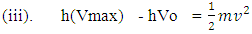 Now by Non-interactive mechanicsN+M = 0 (every system is the combination of Non-Intractable particle and Matter Field )Applying this in equation (iii).
Now by Non-interactive mechanicsN+M = 0 (every system is the combination of Non-Intractable particle and Matter Field )Applying this in equation (iii).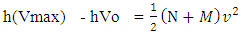
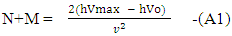 As according to the N-I mechanics equationsN+M = ±fp.o.f ( which is process of formation p.o.f )So equation –A1 becomes
As according to the N-I mechanics equationsN+M = ±fp.o.f ( which is process of formation p.o.f )So equation –A1 becomes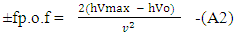 Now if we look the mass-energy relativistic relation is
Now if we look the mass-energy relativistic relation is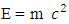 where c is speed of light or photonsAccording to Non-interactive mechanicsN+M = 0 where N is non-intractable particle and M is matter, this suggest the sum of N-I particle and Matter is equals to class zero particles. Also every system is the combination of Non-intractable particle and Matter.Applying this in mass-energy relation
where c is speed of light or photonsAccording to Non-interactive mechanicsN+M = 0 where N is non-intractable particle and M is matter, this suggest the sum of N-I particle and Matter is equals to class zero particles. Also every system is the combination of Non-intractable particle and Matter.Applying this in mass-energy relation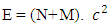 This equation can be represent as
This equation can be represent as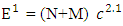
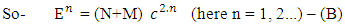 Here c are those particle which remains after the collision of positive and negative curve geometryMathematically, the velocity of light is
Here c are those particle which remains after the collision of positive and negative curve geometryMathematically, the velocity of light is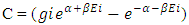 So equation –(B) becomes
So equation –(B) becomes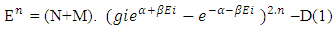 As N+M = ±fp.o.f
As N+M = ±fp.o.f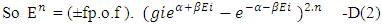 Now applying equation –A(1) and –A(2) in –D(1) and D(2)So-
Now applying equation –A(1) and –A(2) in –D(1) and D(2)So- 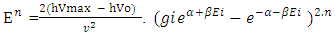 So three equations are
So three equations are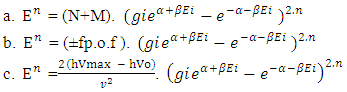 So the combined forms of these relations are
So the combined forms of these relations are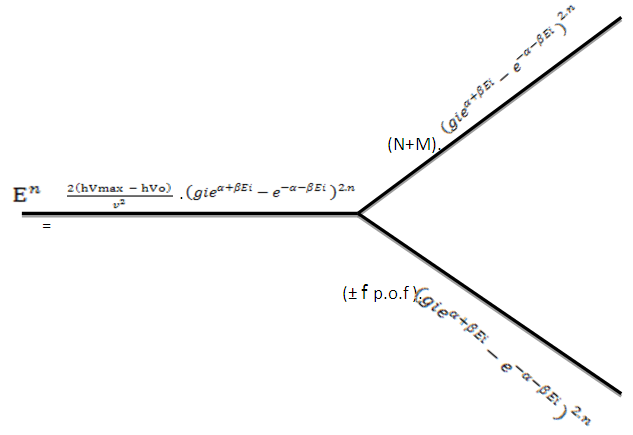
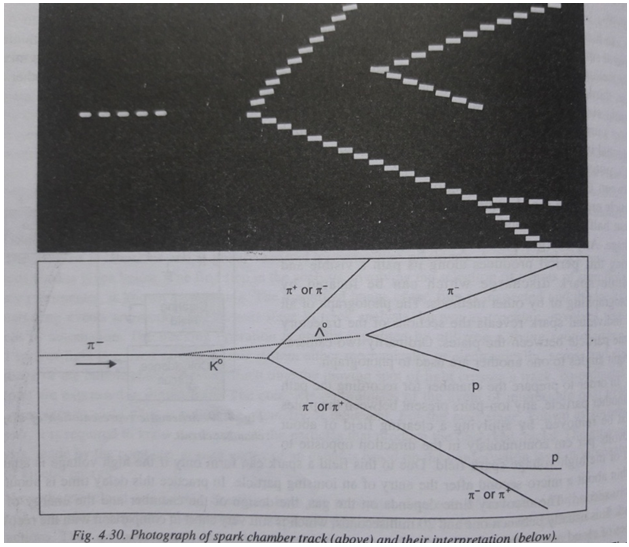 The picture is showing the similar result as mentioned in the above equation so the relation could define particles their nature.
The picture is showing the similar result as mentioned in the above equation so the relation could define particles their nature.
5. Some Non-interactive Phenomenas
i. Non-intractable Particle attend field’s nature before getting it’s physical intractable mass form-by Non-interactive mechanics the corresponding N is given by - 1/12 or 12N = -1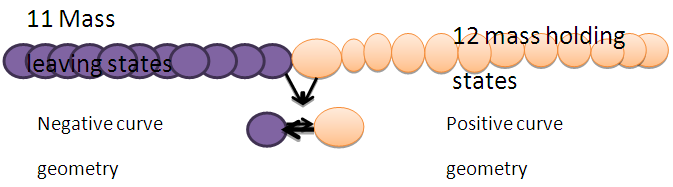 So the only misbalance in both states is the 1 mass holding state which is actually the cell holding particle entering in the matter field (M), so this gives the first positive curve geometry cell holding Particle is beyond the matter field, as entering in this cell non-intractable particle gain the field’s nature and qualities, before getting the physical form.“this gives the general idea that actions starts before they come to sense, or actions starts before their appearance seems physically”.(ii). The first particle enter in the matter field is positively rotating (R.H.R), so positive curve geometry is the prime geometry.The cell distribution formula for the non-interactive mechanics is
So the only misbalance in both states is the 1 mass holding state which is actually the cell holding particle entering in the matter field (M), so this gives the first positive curve geometry cell holding Particle is beyond the matter field, as entering in this cell non-intractable particle gain the field’s nature and qualities, before getting the physical form.“this gives the general idea that actions starts before they come to sense, or actions starts before their appearance seems physically”.(ii). The first particle enter in the matter field is positively rotating (R.H.R), so positive curve geometry is the prime geometry.The cell distribution formula for the non-interactive mechanics is 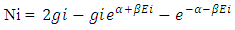 Now this equation suggesting that first particle which entering in the matter field, occupied the cell provided to it and it gives the nature of positively rotating under positive curve geometry.This gives the idea of first particle entering in matter field is positively rotating or following positive curve geometry.So if the field is generally define as –
Now this equation suggesting that first particle which entering in the matter field, occupied the cell provided to it and it gives the nature of positively rotating under positive curve geometry.This gives the idea of first particle entering in matter field is positively rotating or following positive curve geometry.So if the field is generally define as –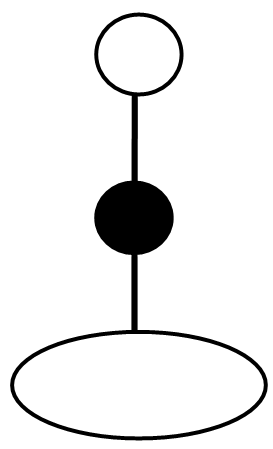 According to Dirac’s particle –antiparticle theory these charge distribution should treated as matter and antimatter, as non-intractable particle enter in the positive curve geometry so-This gives the idea of “matter is more in universe correspond to it anti-matter”.(iii). Universe posses the mechanism of continuous creation and destruction-The supreme mechanics diagram states that 11th mass leaving and 12th mass holding states are co- bindingly creating the physical world’s phenomena.Here 11 mass leaving state continuously mass leaving it’s state which are under negative curve geometry
According to Dirac’s particle –antiparticle theory these charge distribution should treated as matter and antimatter, as non-intractable particle enter in the positive curve geometry so-This gives the idea of “matter is more in universe correspond to it anti-matter”.(iii). Universe posses the mechanism of continuous creation and destruction-The supreme mechanics diagram states that 11th mass leaving and 12th mass holding states are co- bindingly creating the physical world’s phenomena.Here 11 mass leaving state continuously mass leaving it’s state which are under negative curve geometry 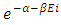 , while the 12th mass holding state continuously holding the mass states and with it the other 11 mass holding states are also attending the mass states.Where the similar in amount but different in rotation and property 11 mass leaving state is also present with negative curve geometrySo 11 mass holding state = 11 mass leaving stateWhere 1 one particle attending the mass field continuously holding the mass field.This give the continuous process of mechanisms creation and destruction where creation is prime.(iv). Every Physical particle is the combination of the N-i particle and Mass field (M)-Now generally the laws of physics are written as-
, while the 12th mass holding state continuously holding the mass states and with it the other 11 mass holding states are also attending the mass states.Where the similar in amount but different in rotation and property 11 mass leaving state is also present with negative curve geometrySo 11 mass holding state = 11 mass leaving stateWhere 1 one particle attending the mass field continuously holding the mass field.This give the continuous process of mechanisms creation and destruction where creation is prime.(iv). Every Physical particle is the combination of the N-i particle and Mass field (M)-Now generally the laws of physics are written as-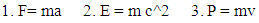 now all the quantities are positive matter field’s and the intractable properties of (F, E, P) and their effects in physical world can be easily observe.By N-I mechanics this type of force is under positive curve geometry or in other words under positive matter field by the cell distribution formula
now all the quantities are positive matter field’s and the intractable properties of (F, E, P) and their effects in physical world can be easily observe.By N-I mechanics this type of force is under positive curve geometry or in other words under positive matter field by the cell distribution formula  positive curve geometry is cell occupied geometry so for the matter field of positive curve geometry all the matter is the combination with it’s N-I particle orN + M = 0So the physical formula according to non-interactive mechanics is
positive curve geometry is cell occupied geometry so for the matter field of positive curve geometry all the matter is the combination with it’s N-I particle orN + M = 0So the physical formula according to non-interactive mechanics is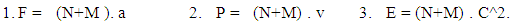 For N=0 or Non-Intractable particle is not present in matter field above equations become
For N=0 or Non-Intractable particle is not present in matter field above equations become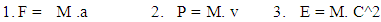
6. Proofs
 This is mass energy equivalence law.Velocity of light
This is mass energy equivalence law.Velocity of light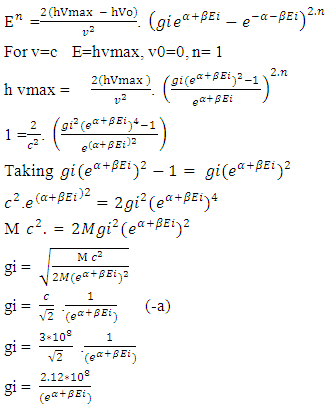
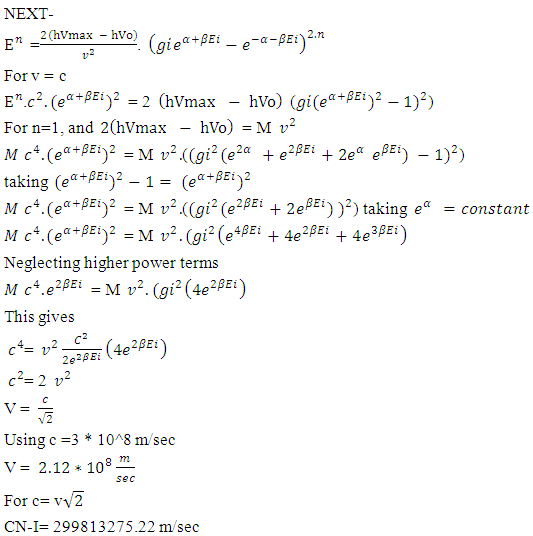 And the current velocity of light is c= 299792458m/secSo the difference is 20817.22 m/secThis gives particles faster than light and also termed as approximation of velocity of light.THE RELATIVISTIC CONDITION
And the current velocity of light is c= 299792458m/secSo the difference is 20817.22 m/secThis gives particles faster than light and also termed as approximation of velocity of light.THE RELATIVISTIC CONDITION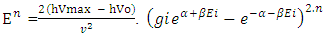 AS n=1 and
AS n=1 and 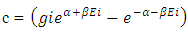
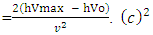 By photo electric effect
By photo electric effect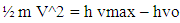 Applying this gives
Applying this gives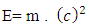 By non-interactive mechanicsN = -MMultiplying -1 on both sides gives
By non-interactive mechanicsN = -MMultiplying -1 on both sides gives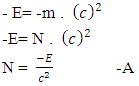 Later
Later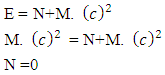 Putting in A gives
Putting in A gives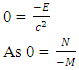 Equating both equation gives
Equating both equation gives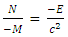 This gives
This gives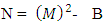 Next-
Next-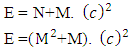 Squaring on both sides
Squaring on both sides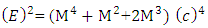 Neglecting higher power terms
Neglecting higher power terms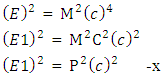 Then
Then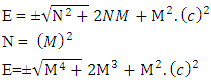 Neglecting higher power terms
Neglecting higher power terms Now squiring gives
Now squiring gives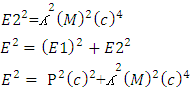 THEORTICLE AND EXPERIMENTAL PROOFS OF NON-INTERACTIVE MECHANICS-(i). Dirac’s theory of particle-antiparticle and positron as a proof -Every Electron posses both positive curve geometry’s dense energy and negative curve geometry’s spread energy or in other word every electron posses right handed and left handed rotation property . as by cell distribution formula for N-I particles
THEORTICLE AND EXPERIMENTAL PROOFS OF NON-INTERACTIVE MECHANICS-(i). Dirac’s theory of particle-antiparticle and positron as a proof -Every Electron posses both positive curve geometry’s dense energy and negative curve geometry’s spread energy or in other word every electron posses right handed and left handed rotation property . as by cell distribution formula for N-I particles 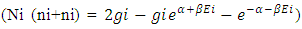 every N-I particle is comes in pair in which one is positive curve geometry particle and another is negative curve geometry particle this is same as ‘DIRAC’S ‘PARTICLE – ANTIPARTICLE’ THEORY ’, also justify the EXISTENSE OF POSITIVE ELECTRON ‘POSITRON’ WHICH IS SAME AS THEORTICLE AND EXPERIMENTAL RESULTS.(ii). Electrons posses both positive curve geometry’s ‘dense field energy and right hand rotation and also negative curve geometry’s spread field energy and it’s left hand rotation Which justify the positive and right hand rotating electron or ‘POSITRON’WHICH IS SAME AS THEORTICLE AND EXPERIMENTAL RESULTS.
every N-I particle is comes in pair in which one is positive curve geometry particle and another is negative curve geometry particle this is same as ‘DIRAC’S ‘PARTICLE – ANTIPARTICLE’ THEORY ’, also justify the EXISTENSE OF POSITIVE ELECTRON ‘POSITRON’ WHICH IS SAME AS THEORTICLE AND EXPERIMENTAL RESULTS.(ii). Electrons posses both positive curve geometry’s ‘dense field energy and right hand rotation and also negative curve geometry’s spread field energy and it’s left hand rotation Which justify the positive and right hand rotating electron or ‘POSITRON’WHICH IS SAME AS THEORTICLE AND EXPERIMENTAL RESULTS.
7. Results
1. The distribution law for N-i Particles is 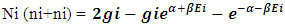 .2. A field quanta is the union of N-i particle and matter, according to the formula N+M=0.3. Energy and size of a Non-intractable particle is give by the equation
.2. A field quanta is the union of N-i particle and matter, according to the formula N+M=0.3. Energy and size of a Non-intractable particle is give by the equation 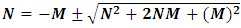 the equation shows same order as Masonic x-ray detection of nucleus radius
the equation shows same order as Masonic x-ray detection of nucleus radius 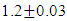 fm.This is also same as deuterons binding energy
fm.This is also same as deuterons binding energy 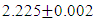 Mev.4. In the process of attending matter field N-I particles change into elementary particles like proton, electron, positron5. According to Non-interactive mechanics the movement of non intractable particles happens before it comes in the sense of physical observation.6. The laws of Physics where Mass is mentioned should improvised, it should written as “N+M” in place of only ‘M’, such as
Mev.4. In the process of attending matter field N-I particles change into elementary particles like proton, electron, positron5. According to Non-interactive mechanics the movement of non intractable particles happens before it comes in the sense of physical observation.6. The laws of Physics where Mass is mentioned should improvised, it should written as “N+M” in place of only ‘M’, such as 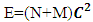 in above manuscript this relation satisfies the relativistic condition
in above manuscript this relation satisfies the relativistic condition 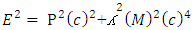 with the relation
with the relation 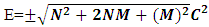 .7.Non-intractable particles are faster than the velocity of light, as the velocity of non-intractable particle is CN-I= 299813275.22 m/sec and current velocity of light is c= 299792458m/sec so Non-intractable particles are20817.22 m/sec faster than light.8. Every reaction of N-I particles in universe follows “Nishant Effect”, here the energy of N-i Particle follows tri-nature property, these energies are
.7.Non-intractable particles are faster than the velocity of light, as the velocity of non-intractable particle is CN-I= 299813275.22 m/sec and current velocity of light is c= 299792458m/sec so Non-intractable particles are20817.22 m/sec faster than light.8. Every reaction of N-I particles in universe follows “Nishant Effect”, here the energy of N-i Particle follows tri-nature property, these energies are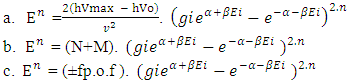 These relations satisfies the conditions ofi. Linear harmonic oscillator E=1/2 hvii. Plank’s radiation law E= hviii. Einstein mass-energy equivalence relation E= mc^2iv. Relativistic condition
These relations satisfies the conditions ofi. Linear harmonic oscillator E=1/2 hvii. Plank’s radiation law E= hviii. Einstein mass-energy equivalence relation E= mc^2iv. Relativistic condition 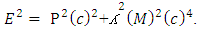 9. The structure of Nucleus and atom according to Non-Interactive Mechanics in manuscript shows same view as LIGO Experiment.
9. The structure of Nucleus and atom according to Non-Interactive Mechanics in manuscript shows same view as LIGO Experiment.
8. Conclusions
1. Field quantas of a corresponding field are the union of Non-intractable particles and matter. So we reach to the point that a field quanta is not only composed of matter only but a independent particle N-I particle makes union with matter to create a field quanta, the relation is given as N+M=0.2. For starting the process of formation of Nucleus and atom, Non-Intractable particle emits matter field, this disintegrated matter react with the process of formation 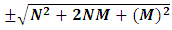 and creates the radius and binding energy of Nucleus and Atom The relation is given as
and creates the radius and binding energy of Nucleus and Atom The relation is given as 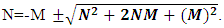 3. The Entering of N-I particles in matter field happens according to the process mentioned in Ramanujan Entering and the exchange of Non-Intractable particles happens according to the Ramanujan Effect.4. The disintegrated matter according to the formula
3. The Entering of N-I particles in matter field happens according to the process mentioned in Ramanujan Entering and the exchange of Non-Intractable particles happens according to the Ramanujan Effect.4. The disintegrated matter according to the formula  divides into two forms first is “dense energy field” which follows clockwise rotation and “spread energy field” which follows anticlockwise rotation in these energy fields Non-Intractable particles enter and follows the respective fields nature and gain energy in form of mass (as E is proportional m) due to this process particles like proton, electron, positrons forms.5. Non-intractable particles holds the nature to follow and fields properties such as spin, charge, mass, energy.6. After entering in matter field matter every Non-intractable particle follows Nishant Effect to gain matter field.
divides into two forms first is “dense energy field” which follows clockwise rotation and “spread energy field” which follows anticlockwise rotation in these energy fields Non-Intractable particles enter and follows the respective fields nature and gain energy in form of mass (as E is proportional m) due to this process particles like proton, electron, positrons forms.5. Non-intractable particles holds the nature to follow and fields properties such as spin, charge, mass, energy.6. After entering in matter field matter every Non-intractable particle follows Nishant Effect to gain matter field.
References
| [1] | Weyl fermions semimetal with surface Fermi arcs in the transition metal monopnictide TaAs class Nature communications 6, Article No: 7373, Doi:10.1038/ncomms8373. |
| [2] | Satya Prakash, “statistical Mechanics”, KNRN, 2015. |
| [3] | Gupta, S.L.,” Elementary Statistical Mechanics”, Pragati Prakashan, 2017. |
| [4] | Tayal, D.C, “Nuclear Physics”, Himalya Publishing House, 2017. |
| [5] | Burcham, W.E., “Nuclear Physics an Introduction”, Longman, 1973. |
| [6] | Frisch, O.R (Editor), “Progress in Nuclear Physics”, pergamon Press, 1959. |
| [7] | Marmier Pierre and Eric Sheldon, “Physics of Nuclei and Particles”, vol. I Academic Press, 1969. |
| [8] | Paul, E.B., “Nuclear and Particle Physics”, North Holland Publishing Co., 1969. |
| [9] | Smith, C.M.S, “A TEXT Book of Nuclear Physics”, Pergamon Press, Oxford, 1966. |
| [10] | http://www.blastr.com/2015-11-4/nasa-just-saw-something-come-out-black-hole-first-time-ever. |






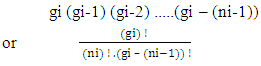
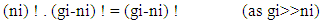 So the equation –(2) looks as:-
So the equation –(2) looks as:-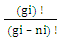
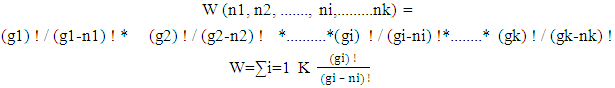
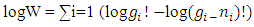 Now using stirling approximation:-Which is - log ni ! = ni log ni – ni
Now using stirling approximation:-Which is - log ni ! = ni log ni – ni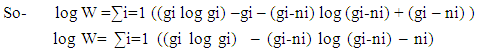
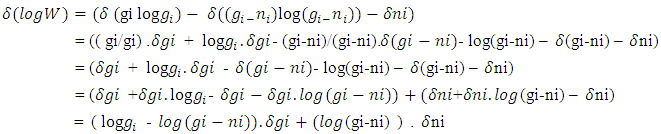
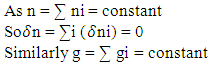
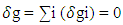 (ii) conservation of total Energy of system for particles and cells –
(ii) conservation of total Energy of system for particles and cells –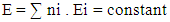
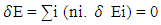 Similarly for gi
Similarly for gi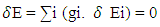 Substituting this in eq.-(6)
Substituting this in eq.-(6)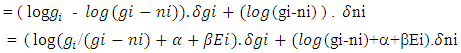
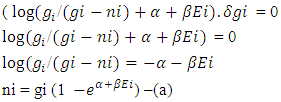 SECOND PART –
SECOND PART –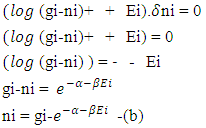 adding both eq. –a and –b substituting this in eq.-(7)
adding both eq. –a and –b substituting this in eq.-(7)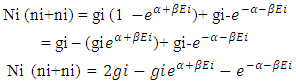
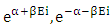 = geometries available to non-interactible particles.Now we discuss the behaviour of eq-(8) and process of cell distribution to non-interactible particles, as the existence of these particles is stated in 0hv energy level and the non-interactive mechanics deals with the mechanism of non-intractable particle from 0.hv energy level to 0.5hv energy level which can be stated as matter field, so in equation –(8) Ni represents the number of non-intractable particles, so as 2 non-intractable particle entered in matter field the 2 two cells (2gi) are provided to them, with two geometries of matter field
= geometries available to non-interactible particles.Now we discuss the behaviour of eq-(8) and process of cell distribution to non-interactible particles, as the existence of these particles is stated in 0hv energy level and the non-interactive mechanics deals with the mechanism of non-intractable particle from 0.hv energy level to 0.5hv energy level which can be stated as matter field, so in equation –(8) Ni represents the number of non-intractable particles, so as 2 non-intractable particle entered in matter field the 2 two cells (2gi) are provided to them, with two geometries of matter field 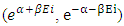 which are equal in amount but diffrent in direction, in which the geometry
which are equal in amount but diffrent in direction, in which the geometry 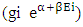 occupy a cell is stated as POSITIVE CURVE GEOMETRY, and the geometry which is equal in amount of positive curve geometry but cell less and oppositein direction is stated as NEGATIVE CURVE GEOMETY.So the points are clear as:-1. At the time of entering of a pair of non-intractable particle in the matter field, there will be two cells are provided to them.2. After the entering of these non-intractable particles in the matter field they comes under the two geometries in matter field (positive and negative curve geometries) which are equal in amount but opposite in direction
occupy a cell is stated as POSITIVE CURVE GEOMETRY, and the geometry which is equal in amount of positive curve geometry but cell less and oppositein direction is stated as NEGATIVE CURVE GEOMETY.So the points are clear as:-1. At the time of entering of a pair of non-intractable particle in the matter field, there will be two cells are provided to them.2. After the entering of these non-intractable particles in the matter field they comes under the two geometries in matter field (positive and negative curve geometries) which are equal in amount but opposite in direction 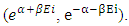 3. As one of the positive curve geometry
3. As one of the positive curve geometry 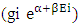 is cell occupied geometry, so the first particle enter in the matter field will follow the positive curve geometry, and with it equal in amount but opposite in direction geometry Negative curve geometry is also provided to non-intractable particle.So the prime rotation followed by non-intractable particles is under positive curve geometry or in other words right-handed rotation is the prime rotation followed by the Non-intractable particles,With it Negative curve geometry (left hand rotation) is also available to the Non-intractable particles which is just equal in amount but different in direction. C. POSITIVE AND NEGATIVE CURVE GEOMETRIESThe concept of curved space geometry is arise by the mathematician Riemann and then in general theory of relativity Einstein gives the description of curved space geometry, here in non-interactive mechanics, space geometry categorise by the different rotation properties of non-interactive particles in matter field.POSITIVE CURVE GEOMETRY-The term
is cell occupied geometry, so the first particle enter in the matter field will follow the positive curve geometry, and with it equal in amount but opposite in direction geometry Negative curve geometry is also provided to non-intractable particle.So the prime rotation followed by non-intractable particles is under positive curve geometry or in other words right-handed rotation is the prime rotation followed by the Non-intractable particles,With it Negative curve geometry (left hand rotation) is also available to the Non-intractable particles which is just equal in amount but different in direction. C. POSITIVE AND NEGATIVE CURVE GEOMETRIESThe concept of curved space geometry is arise by the mathematician Riemann and then in general theory of relativity Einstein gives the description of curved space geometry, here in non-interactive mechanics, space geometry categorise by the different rotation properties of non-interactive particles in matter field.POSITIVE CURVE GEOMETRY-The term 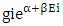 in eq. –(8) represents the positive curve geometry the name positive curve is due to positive signs of
in eq. –(8) represents the positive curve geometry the name positive curve is due to positive signs of 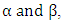 the geometry is a cell occupied positive curve geometry in which the rotation of N-I particles is right handed, rotation of proton in nucleus and all +1/2 (app.) rotating particles follow the positive curve geometry provided in matter field, the positive curve geometry can be explained as the rotation of planets around sun is the positive curve geometry. ‘So the prime rotating geometry is positive curve geometry in the matter field’ now as the cell occupied geometry so the interaction will occurs So “the cell occupied geometry in which the N-I particles follow the right handed rotation is called positive curve geometry”. NEGATIVE CURVE GEOMETRYThe term
the geometry is a cell occupied positive curve geometry in which the rotation of N-I particles is right handed, rotation of proton in nucleus and all +1/2 (app.) rotating particles follow the positive curve geometry provided in matter field, the positive curve geometry can be explained as the rotation of planets around sun is the positive curve geometry. ‘So the prime rotating geometry is positive curve geometry in the matter field’ now as the cell occupied geometry so the interaction will occurs So “the cell occupied geometry in which the N-I particles follow the right handed rotation is called positive curve geometry”. NEGATIVE CURVE GEOMETRYThe term 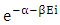 in eq.-(8) represents the negative curve geometry, the name negative curve is due to the negative sign of
in eq.-(8) represents the negative curve geometry, the name negative curve is due to the negative sign of 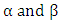 .the geometry is a non cell ocuupied geometry, which is equal in amount to positive curve geometry but diffrent in rotation. D. NON-INTERACTIBLE PARTICLES ENTERING IN MATTER FIELD AND IT’S EXPLANATIONNow we see the equation of entering of non-intractable particles in matter field, this can be seen as the entering of 0hv energy field quanta (N-I particle) in 0.5hv energy field quanta or in intractable matter field.The eq. –(8) represents the distribution of ni Non-intractable particles in gi cell’s which is
.the geometry is a non cell ocuupied geometry, which is equal in amount to positive curve geometry but diffrent in rotation. D. NON-INTERACTIBLE PARTICLES ENTERING IN MATTER FIELD AND IT’S EXPLANATIONNow we see the equation of entering of non-intractable particles in matter field, this can be seen as the entering of 0hv energy field quanta (N-I particle) in 0.5hv energy field quanta or in intractable matter field.The eq. –(8) represents the distribution of ni Non-intractable particles in gi cell’s which is 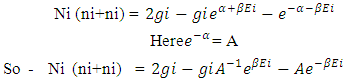
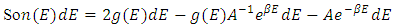
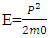 But as we know that particles posses almost zero mass in both rest and moving, so as
But as we know that particles posses almost zero mass in both rest and moving, so as  now here
now here 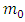 is the approximately equal to zero mass value so-
is the approximately equal to zero mass value so- 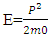 (where m0 is the mass of non-interactible particle approximately equal to zero)so the eq.- (10) transform into:-
(where m0 is the mass of non-interactible particle approximately equal to zero)so the eq.- (10) transform into:-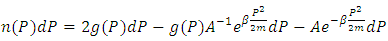
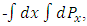 while the volume of one cell is
while the volume of one cell is 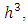 so the point is cleared here that particles have six-dimensional space or may be more to move, but they bound to move in the dimensional space where x is position coordinate and Px is relative momentum, as we choose x and Px axis to move :-
so the point is cleared here that particles have six-dimensional space or may be more to move, but they bound to move in the dimensional space where x is position coordinate and Px is relative momentum, as we choose x and Px axis to move :-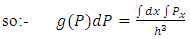
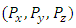 to move but they are bound to move only in straight lineHere
to move but they are bound to move only in straight lineHere 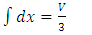 because
because 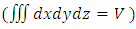 As we know that particle lying in the momentum range between Px and Px+dPx (as six dimensional space x,Px,yPy and z,Pz available but particle bound to move in the straight line) so:-
As we know that particle lying in the momentum range between Px and Px+dPx (as six dimensional space x,Px,yPy and z,Pz available but particle bound to move in the straight line) so:- 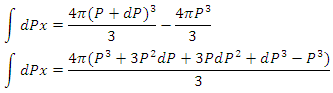
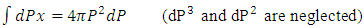
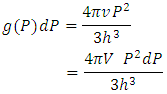 Substituting above value of g(P) dP in equation-(11)
Substituting above value of g(P) dP in equation-(11)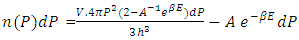 Since the total number of non-intractable particles is N so-
Since the total number of non-intractable particles is N so-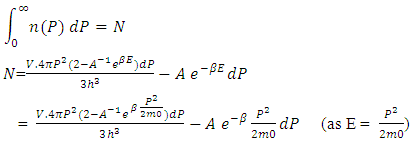 So:-
So:-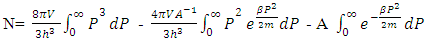 Neglecting the first integral on R.H.S due to integral limits
Neglecting the first integral on R.H.S due to integral limits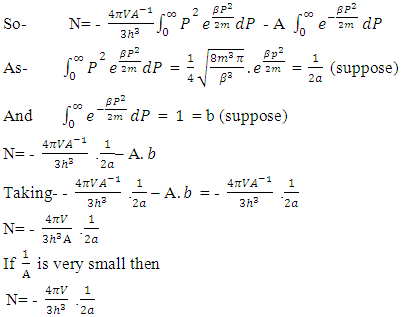
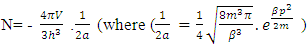
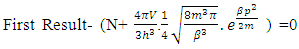
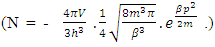
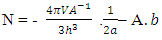 -(12) if the value of
-(12) if the value of 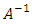 is small then
is small then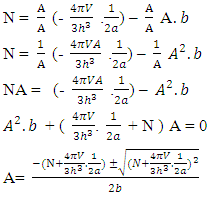
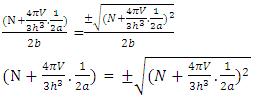 As
As 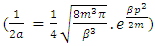 so above mentioned equation turned into-
so above mentioned equation turned into-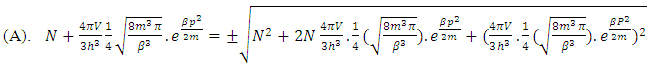
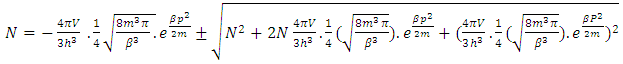
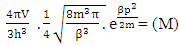 The Matter provided at the time of Entering of N-I Particles.3.
The Matter provided at the time of Entering of N-I Particles.3. 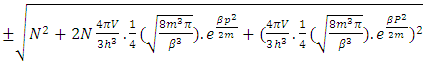 = Distribution of N-I particles and Matter field or simply Process of Formation (f p.o.f).The four equations of non-interactive mechanics are
= Distribution of N-I particles and Matter field or simply Process of Formation (f p.o.f).The four equations of non-interactive mechanics are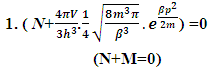 (13a)Here N is (N-I particle) while M is mass field, so the ‘ sum of non-intractable particle and matter field is equal to class zero particle field’. In other word ‘A field quantais the union of non-intractable particle and matter field ’.
(13a)Here N is (N-I particle) while M is mass field, so the ‘ sum of non-intractable particle and matter field is equal to class zero particle field’. In other word ‘A field quantais the union of non-intractable particle and matter field ’.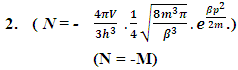 (13b)The equation showing that ‘the non-intractable particle is equal to disintegrated matter’. here the term –M showing the disintegrated matter .
(13b)The equation showing that ‘the non-intractable particle is equal to disintegrated matter’. here the term –M showing the disintegrated matter . 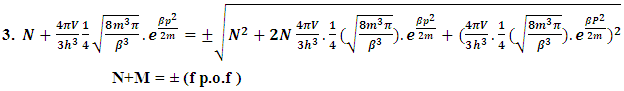 (15)The above shown equation showing that ‘union of N-I particle and matter field is equal to process of formation ’. Now if we equate equation -1 and -3 than we find 1. (N+M=0) 3. N+M = ± (f p.o.f ) 0 = ± (f p.o.f ) so the process of formation is equal to class zero particle .
(15)The above shown equation showing that ‘union of N-I particle and matter field is equal to process of formation ’. Now if we equate equation -1 and -3 than we find 1. (N+M=0) 3. N+M = ± (f p.o.f ) 0 = ± (f p.o.f ) so the process of formation is equal to class zero particle . 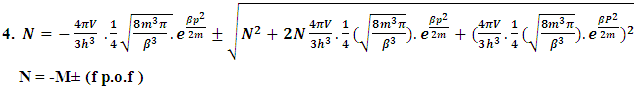 (16)The above shown equation showing that ‘N-I particle is equal to sum of disintegrated matter and the process of formation ‘ . this equation is the N-I particles entering equation in matter field.THIS VALUE IS EQUALS TO THE MESONIC X-RAY OF NUCLEUS RADIUS 1.2+_0.03 fm.This is also same as deuterons binding energy 2.225+_0.002 MevNow let’s see a another case if (N = -M± (f p.o.f) and 0 =± (f p.o.f)So N = -M + 0 The N-I particles are indistinguishable so taking 0 = N + M’ the N-I particle is indistinguishable but theirs variation in matter as they posses interaction property so
(16)The above shown equation showing that ‘N-I particle is equal to sum of disintegrated matter and the process of formation ‘ . this equation is the N-I particles entering equation in matter field.THIS VALUE IS EQUALS TO THE MESONIC X-RAY OF NUCLEUS RADIUS 1.2+_0.03 fm.This is also same as deuterons binding energy 2.225+_0.002 MevNow let’s see a another case if (N = -M± (f p.o.f) and 0 =± (f p.o.f)So N = -M + 0 The N-I particles are indistinguishable so taking 0 = N + M’ the N-I particle is indistinguishable but theirs variation in matter as they posses interaction property so 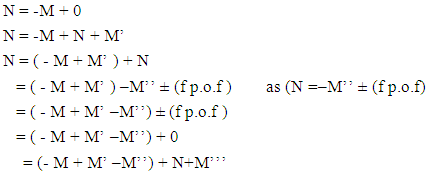 And so as further again this shows the continuous extension of the procedure as this also states that a N-I particle posses the infinite expansion property this states that the process of Non-interactive mechanics is a continues and periodic system in which matter field always extend by every step. Here the meaning represented by the each term in give equation is 1. N=Non-intractable Particle (N-I particle).2.
And so as further again this shows the continuous extension of the procedure as this also states that a N-I particle posses the infinite expansion property this states that the process of Non-interactive mechanics is a continues and periodic system in which matter field always extend by every step. Here the meaning represented by the each term in give equation is 1. N=Non-intractable Particle (N-I particle).2. 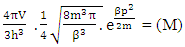 The Matter provided at the time of Entering of N-I Particles.3.
The Matter provided at the time of Entering of N-I Particles.3. 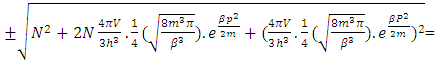 Distribution of N-I particles and Matter field or simply Process of Formation (f p.o.f).Now let’s examine the above equations the each term:-1. ‘N’ the Non-intractable particle- In above mentioned equations the term ‘N’ represents the Non-intractable particle. this term shows varies types of quality in matter field and out of matter field which are.A. Ramanujan Entering.B. Ramanujan Effect.A. Ramanujan Entering:- In above mentioned equations the term N represents the N-I particle, whose interaction with matter field is negligible, so for the matter field particle it become a ideal particle so, mathematically-
Distribution of N-I particles and Matter field or simply Process of Formation (f p.o.f).Now let’s examine the above equations the each term:-1. ‘N’ the Non-intractable particle- In above mentioned equations the term ‘N’ represents the Non-intractable particle. this term shows varies types of quality in matter field and out of matter field which are.A. Ramanujan Entering.B. Ramanujan Effect.A. Ramanujan Entering:- In above mentioned equations the term N represents the N-I particle, whose interaction with matter field is negligible, so for the matter field particle it become a ideal particle so, mathematically-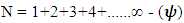 this equation represents that the sum of infinite matter field particle is equal to non-interactible particle.Now multiplying equation
this equation represents that the sum of infinite matter field particle is equal to non-interactible particle.Now multiplying equation 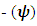 by 4 on both sides then:-
by 4 on both sides then:-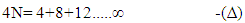 Now substracting equation -(∆) from - (𝝍) we get-
Now substracting equation -(∆) from - (𝝍) we get-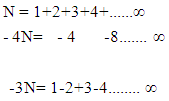 This gives-
This gives-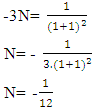
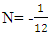 The given terms can be written as 12N = -1 so by the L.H.S and R.H.S we Can see that the 12 Non Intractable particles emits by Field quanta in the direction of positive curve geometry till the condition of 12N arrives and one Non –Intractable particle emits in the direction of Negative curve geometry. After completing the procedure 12N = -1 Matter field is available to Positive curve geometry following Non-Intractable Particles.From this point they have mass field and it’s relative state to attain the mass value provided in field.As the mathematical relation is given by “shri – srinivasn ramanujan”. So the entering of 12 non-intractable particles in mass field by following positive curve geometry while one N-i Particle is following Negative curve Geometry is called as ‘Ramanujan Entering’.
The given terms can be written as 12N = -1 so by the L.H.S and R.H.S we Can see that the 12 Non Intractable particles emits by Field quanta in the direction of positive curve geometry till the condition of 12N arrives and one Non –Intractable particle emits in the direction of Negative curve geometry. After completing the procedure 12N = -1 Matter field is available to Positive curve geometry following Non-Intractable Particles.From this point they have mass field and it’s relative state to attain the mass value provided in field.As the mathematical relation is given by “shri – srinivasn ramanujan”. So the entering of 12 non-intractable particles in mass field by following positive curve geometry while one N-i Particle is following Negative curve Geometry is called as ‘Ramanujan Entering’. (image- NASA)Similar entering procedure observed by NASA when a particle comes out from black hole.This is similar to the theoretical and mathematical results mentioned in ‘Ramanujan Entering’.B. Ramanujan Effect-In Ramanujan effect we will study the exchange process of Non-intractable particles.so Equation -14(a) and equation –14(b) are
(image- NASA)Similar entering procedure observed by NASA when a particle comes out from black hole.This is similar to the theoretical and mathematical results mentioned in ‘Ramanujan Entering’.B. Ramanujan Effect-In Ramanujan effect we will study the exchange process of Non-intractable particles.so Equation -14(a) and equation –14(b) are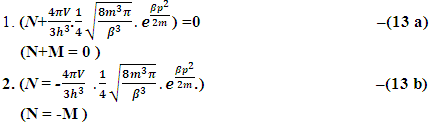 Here
Here  which gives ‘
which gives ‘ ‘ after solution, so here N is equal to app. infinite number of positive curve geometry particle so the above relation can be written as
‘ after solution, so here N is equal to app. infinite number of positive curve geometry particle so the above relation can be written as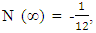 here infinite positive curve geometry particles are the function of Non-intractable Particle. Now taking equation –(13 b)
here infinite positive curve geometry particles are the function of Non-intractable Particle. Now taking equation –(13 b)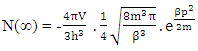 Now multiplying
Now multiplying  on the left of both sides we get
on the left of both sides we get This gives-
This gives-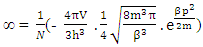
 -equation (i)Also -
-equation (i)Also - 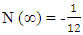 multiplying
multiplying  on the left of both sides we get
on the left of both sides we get
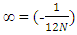
 -equation (ii)Also-
-equation (ii)Also- 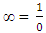
 -equation (iii)This gives -For ∞ this gives the relation
-equation (iii)This gives -For ∞ this gives the relation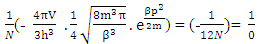
 equation-(18)Now again –(13 b)
equation-(18)Now again –(13 b)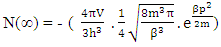 here N is Non-intractable particle , and ∞ represents the infinite number of positive curve geometry particles which are the function of N-I particle.Now taking inverse of above equation –(13 b)
here N is Non-intractable particle , and ∞ represents the infinite number of positive curve geometry particles which are the function of N-I particle.Now taking inverse of above equation –(13 b)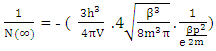 Multiplying by N on both sides of given equation
Multiplying by N on both sides of given equation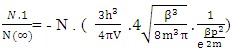 Now multiplying
Now multiplying  on numerator and denominator both this gives-
on numerator and denominator both this gives-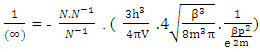 Which gives-
Which gives-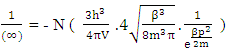
 -equation (j)As
-equation (j)As 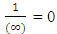 So -
So - 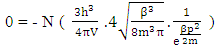
 -equation (jj)Also-
-equation (jj)Also- 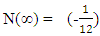 Taking inverse on both sides we get-
Taking inverse on both sides we get-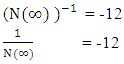 Multiplying
Multiplying 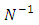 on the denomenator of both sidesFirst the equation can be written as
on the denomenator of both sidesFirst the equation can be written as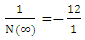 Now
Now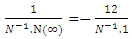 Which gives
Which gives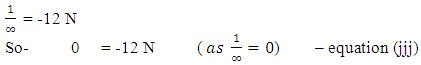 Now examining the above equations (i) and (jj) are-
Now examining the above equations (i) and (jj) are-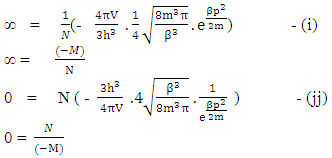 The above shown equations shows that from equation -14(a) and -14(b)1. N+M=0, 2. N= -MThe union or sum of element and matter creates a field quanta and as disintegration of matter occurs after that this disintegrate matter collide with field quanta which creates two views or phenomena which are –when
The above shown equations shows that from equation -14(a) and -14(b)1. N+M=0, 2. N= -MThe union or sum of element and matter creates a field quanta and as disintegration of matter occurs after that this disintegrate matter collide with field quanta which creates two views or phenomena which are –when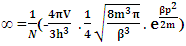
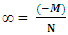 (here N is non-interactible particle and -M is disintegrate mass)From this view all the mechanism is seems as ∞, in other words in this view disintegrated matter is always increase with every step.So as
(here N is non-interactible particle and -M is disintegrate mass)From this view all the mechanism is seems as ∞, in other words in this view disintegrated matter is always increase with every step.So as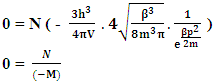 From this view all the mechanism is seems as 0, in other words in this view field quantas continuously emits.So “The Non-intractable Particle and matter creates field quantas, this creates two views of same phenomenaIn which one view represents view of ∞ (the view where matter continuously disintegrates)and one view shows the view of zero 0(where field quantas continuously emit ) by both of these view field quantas and matter fields exchange by each other views, This is ‘Ramanujan effect’ for disintegrate matter and N-I Particle”.
From this view all the mechanism is seems as 0, in other words in this view field quantas continuously emits.So “The Non-intractable Particle and matter creates field quantas, this creates two views of same phenomenaIn which one view represents view of ∞ (the view where matter continuously disintegrates)and one view shows the view of zero 0(where field quantas continuously emit ) by both of these view field quantas and matter fields exchange by each other views, This is ‘Ramanujan effect’ for disintegrate matter and N-I Particle”.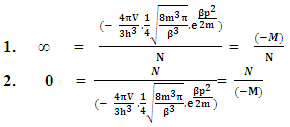

 3. The Interaction of Non-Intractable Particles with Matter (M)- The mass term (M) in above equations shown as –
3. The Interaction of Non-Intractable Particles with Matter (M)- The mass term (M) in above equations shown as –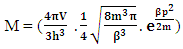 For the disintegrated matter the term also appear as –
For the disintegrated matter the term also appear as –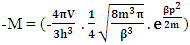 By equation -14(a) and -14(b) we see that-
By equation -14(a) and -14(b) we see that- The sum of N-I particle and Matter creates field quanta and by equation -14(b) the non-intractable particle is equal to disintegrated matter. The qualities of this mass (M) field are-As N-i particle follow ramanujan entering procedure by following the relation 12 N = -1, this equation states that 12 Positive curve geometry following particle is equal to the negative curve geometry following one N-I particle, so at this point positive curve geometry and the relative mass of the field is also available for N-I Particle.“After entering in the Matter field the N-I particle is surrounded by the region of
The sum of N-I particle and Matter creates field quanta and by equation -14(b) the non-intractable particle is equal to disintegrated matter. The qualities of this mass (M) field are-As N-i particle follow ramanujan entering procedure by following the relation 12 N = -1, this equation states that 12 Positive curve geometry following particle is equal to the negative curve geometry following one N-I particle, so at this point positive curve geometry and the relative mass of the field is also available for N-I Particle.“After entering in the Matter field the N-I particle is surrounded by the region of 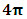 which posses the volume of
which posses the volume of 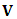
 here in this region the 3 types of mass attending method is available to each N-I particle, each method posses the degree of freedom of
here in this region the 3 types of mass attending method is available to each N-I particle, each method posses the degree of freedom of 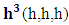 this state of N-I Particle is known as ‘ 3-Gate Body’, so the region of
this state of N-I Particle is known as ‘ 3-Gate Body’, so the region of 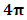 with volume of
with volume of 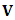
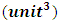 with ‘ 3-Gate Body’ in which each posses degree of freedom of
with ‘ 3-Gate Body’ in which each posses degree of freedom of 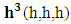 is available to N-I particle.After attending 3-Gate body N-I particle is ready to attend the mass of field. now the mass potential is
is available to N-I particle.After attending 3-Gate body N-I particle is ready to attend the mass of field. now the mass potential is 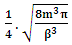 here this term is seems as fourth part of mass potential, so each mass field posses 4- mass potential, This potentials are named as “Mass-Particle Directors” Or simply ‘M-P Directors’, here each M-P director posses the region of
here this term is seems as fourth part of mass potential, so each mass field posses 4- mass potential, This potentials are named as “Mass-Particle Directors” Or simply ‘M-P Directors’, here each M-P director posses the region of 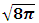 and the mass value of
and the mass value of 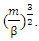 so after attending ‘9-Gate Body’ and “4-Mass-Particle Directors” N-I Particle start to gain the mass of the field.
so after attending ‘9-Gate Body’ and “4-Mass-Particle Directors” N-I Particle start to gain the mass of the field. The image of this particle is captured by NASA.The term
The image of this particle is captured by NASA.The term 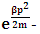 This exponential term is mentioned in two forms
This exponential term is mentioned in two forms 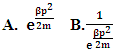 The part A gives the view of ∞ (to gain Matter field) due to this N-I particle seems to expand exponentially with the expansion rate of
The part A gives the view of ∞ (to gain Matter field) due to this N-I particle seems to expand exponentially with the expansion rate of 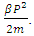 The part B gives the view of 0, from this view only the Non-intractable particles expand and joint with other N-I particles with The rate of
The part B gives the view of 0, from this view only the Non-intractable particles expand and joint with other N-I particles with The rate of 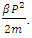
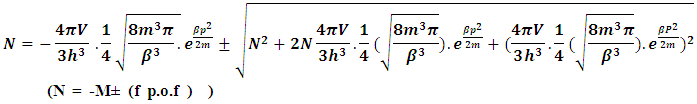 (17)Here the part-
(17)Here the part-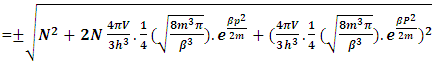 is described as process of formationOr simply f(p.o.f), now opening this above equation-
is described as process of formationOr simply f(p.o.f), now opening this above equation- 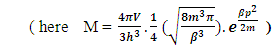
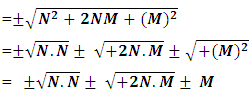
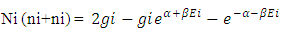 two cells are provided to every N-I particle as where the first cell holding particle is positive curve geometry particle and will follow right hand rotation while negative curve geometry is also available in the field, so as by equation-(19) we can see two sign variations are available in above equation-(19) Which are
two cells are provided to every N-I particle as where the first cell holding particle is positive curve geometry particle and will follow right hand rotation while negative curve geometry is also available in the field, so as by equation-(19) we can see two sign variations are available in above equation-(19) Which are 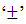 neutral field cell,‘+’ positive field cell so equation –(19) states that two N-I particles
neutral field cell,‘+’ positive field cell so equation –(19) states that two N-I particles 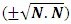 are entering from 0 energy field, then these two particles entering in the matter field
are entering from 0 energy field, then these two particles entering in the matter field 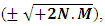 this matter field is ‘dense energy field’
this matter field is ‘dense energy field’ 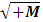 and positive curve geometry field but as the cell distribution formula states as their’s one cell for positive curve geometry particle while other cell is for neutral field particle, so one N-I particle will stay in this field and obtain the relative field’s mass this positive curved geometry’s cell occupied stable and right-hand rotating particle is ‘PROTON’. while the second N-I particle will also enter in this ‘dense energy field ‘ (as equation stating that
and positive curve geometry field but as the cell distribution formula states as their’s one cell for positive curve geometry particle while other cell is for neutral field particle, so one N-I particle will stay in this field and obtain the relative field’s mass this positive curved geometry’s cell occupied stable and right-hand rotating particle is ‘PROTON’. while the second N-I particle will also enter in this ‘dense energy field ‘ (as equation stating that 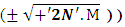 but the only cell ispresent in this field is occupied so this second N-I particle will collect some mass from positively curved dense energy field and transmit to the ‘spread energy field
but the only cell ispresent in this field is occupied so this second N-I particle will collect some mass from positively curved dense energy field and transmit to the ‘spread energy field 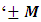 and as cell distribution formula this spread enrgy field is under meutral field particle and follow negative curve geometry this spread energy field particle, which is left-handed rotating and following negative curve geometry and also unstable in dense energy field and positive curve geometry is ‘ELECTRON’.4. NUCLEUS AND ATOM THE MOST STABLE STATEThe points are clear by non-intractable mechanics are-1. 2 cells are provided to non-intractable particles, in which one is for positive curve geometry particle, while another one is not filled by another non-intractable particle.2. As negative curve geometry is cell less so this cell can’t be filled by not the positive curve geometry particle neither negative curve geometry particle, so this is the second cell will be filled by the neutral particle (+,0,-).3. energy of field is distributed in two parts - 1. Dense energy field 2. Spread energy field.4. two types of field geometry is provided which are-i. positive curve geometry .ii. negative curve geometry.5. the geometries are divide into four parts in which first part isi. pure positive curve geometry and maintained positive curve geometry.ii. pure negative geometry and maintained negative curve geometry.6. (i) pure positive curve geometry is controlled by it’s cell holding particle
and as cell distribution formula this spread enrgy field is under meutral field particle and follow negative curve geometry this spread energy field particle, which is left-handed rotating and following negative curve geometry and also unstable in dense energy field and positive curve geometry is ‘ELECTRON’.4. NUCLEUS AND ATOM THE MOST STABLE STATEThe points are clear by non-intractable mechanics are-1. 2 cells are provided to non-intractable particles, in which one is for positive curve geometry particle, while another one is not filled by another non-intractable particle.2. As negative curve geometry is cell less so this cell can’t be filled by not the positive curve geometry particle neither negative curve geometry particle, so this is the second cell will be filled by the neutral particle (+,0,-).3. energy of field is distributed in two parts - 1. Dense energy field 2. Spread energy field.4. two types of field geometry is provided which are-i. positive curve geometry .ii. negative curve geometry.5. the geometries are divide into four parts in which first part isi. pure positive curve geometry and maintained positive curve geometry.ii. pure negative geometry and maintained negative curve geometry.6. (i) pure positive curve geometry is controlled by it’s cell holding particle 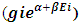 (ii). All three geometries are controlled by neutral cell occupied particle.So the figure according to these details is –
(ii). All three geometries are controlled by neutral cell occupied particle.So the figure according to these details is – This is the figure of stable state’ nucleus and atom.
This is the figure of stable state’ nucleus and atom. This is the LIGO Experiment BY which Gravitational waves was detected shows same structure as above structure of Nucleus and atom according to Non-Interactive Mechanics.
This is the LIGO Experiment BY which Gravitational waves was detected shows same structure as above structure of Nucleus and atom according to Non-Interactive Mechanics.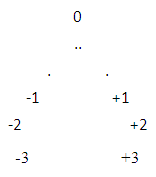 A neutral field is required for the production of any reaction, thus any reaction when collision occurs the reaction will be stable.(v). According to the non-interactive mechanics cell distribution formula.
A neutral field is required for the production of any reaction, thus any reaction when collision occurs the reaction will be stable.(v). According to the non-interactive mechanics cell distribution formula.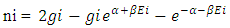 in this equation two cells are provided and positive cure geometry is prime and a cell occupied geometry, so in this case ‘Number of particles is always greater than number of Anti-particles’, as according to the non-interactive mechanics first particle enter in the matter field is goes under positive curve geometry and R.H rotating particle.So due to this point the number figure will be
in this equation two cells are provided and positive cure geometry is prime and a cell occupied geometry, so in this case ‘Number of particles is always greater than number of Anti-particles’, as according to the non-interactive mechanics first particle enter in the matter field is goes under positive curve geometry and R.H rotating particle.So due to this point the number figure will be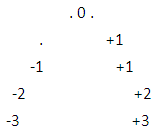 The number of particles is near to neutral field rather than Anti-particles.Non-Interactive mechanics four equations-
The number of particles is near to neutral field rather than Anti-particles.Non-Interactive mechanics four equations-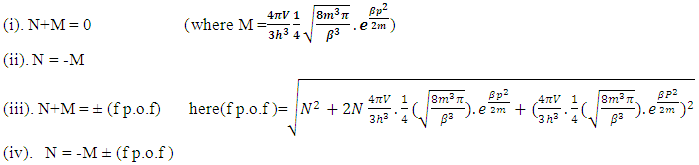 Now from equation (iv)N = -M ± (f p.o.f)So N = -M + 0The N-I particles are indistinguishable so taking 0 = N + M’ the N-I particle is indistinguishable but theirs variation in matter as they posses interaction property so
Now from equation (iv)N = -M ± (f p.o.f)So N = -M + 0The N-I particles are indistinguishable so taking 0 = N + M’ the N-I particle is indistinguishable but theirs variation in matter as they posses interaction property so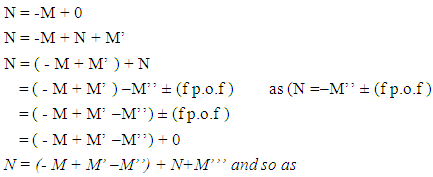 “Matter field is continuously increasing after the production of non-intractable particles”.‘In case of non-intractable particle the positive curve geometry’s matter always increase by the production of new non-intractable particle, with respect to negative curve geometry’s matter.(vii). So the required steps are-As mentioned in non-interactive mechanics the two geometries are (i). Positive Curve Geometry, (ii). Negative Curve GeometryThe positive geometry is possessing 12 mass holding states while negative is possessing 11 mass leaving states –Where these mass leaving states posses cell less geometry, so in that condition negative curve geometry continuously proceed till the Non-intractable particle emit, here the available matter field quality is tri nature.3.2 NISHANT EFFECT- “ANY REACTION OR PHENOMENA IS CAN’T BE POSSIBLE TILL MATTER FIELD DOESN’T FOLLOW TRI-NATURE PROPERTY AND NEGATIVE CURVE GEOMETRY AND NOT ANY N-I PARTICLES ENTER IN THE POSITIVE CURVE GEOMETRY’S MAXIMUM EXCITING STATE. WHERE THE NUMBER OF PARTICLES IS ALWAYS GREATER THAN IT’S RELATIVE ANTI-PARTICLES, AND BY PRODUCTION OF THESE NON-INTRACTABLE PARTICLE MATTER FIELD ALWAYS INCREASE”.3.3 EQUATIONS AND PROOFS (Spark Chamber Photos)-(i). The total energy of a reaction is given by-
“Matter field is continuously increasing after the production of non-intractable particles”.‘In case of non-intractable particle the positive curve geometry’s matter always increase by the production of new non-intractable particle, with respect to negative curve geometry’s matter.(vii). So the required steps are-As mentioned in non-interactive mechanics the two geometries are (i). Positive Curve Geometry, (ii). Negative Curve GeometryThe positive geometry is possessing 12 mass holding states while negative is possessing 11 mass leaving states –Where these mass leaving states posses cell less geometry, so in that condition negative curve geometry continuously proceed till the Non-intractable particle emit, here the available matter field quality is tri nature.3.2 NISHANT EFFECT- “ANY REACTION OR PHENOMENA IS CAN’T BE POSSIBLE TILL MATTER FIELD DOESN’T FOLLOW TRI-NATURE PROPERTY AND NEGATIVE CURVE GEOMETRY AND NOT ANY N-I PARTICLES ENTER IN THE POSITIVE CURVE GEOMETRY’S MAXIMUM EXCITING STATE. WHERE THE NUMBER OF PARTICLES IS ALWAYS GREATER THAN IT’S RELATIVE ANTI-PARTICLES, AND BY PRODUCTION OF THESE NON-INTRACTABLE PARTICLE MATTER FIELD ALWAYS INCREASE”.3.3 EQUATIONS AND PROOFS (Spark Chamber Photos)-(i). The total energy of a reaction is given by-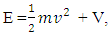 here E is total energy of a reaction
here E is total energy of a reaction 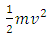 is kinetic energy and V is potential energy(ii). Now the system where photonic decays are is proceeding the kinetic energy of that phenomena is represented as
is kinetic energy and V is potential energy(ii). Now the system where photonic decays are is proceeding the kinetic energy of that phenomena is represented as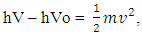 here hV is the energy (E) of a system while hVo is work function and
here hV is the energy (E) of a system while hVo is work function and 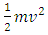 is kinetic energy of the system.If the matter is following try-nature property than dividing the frequency of E = hV in three parts.
is kinetic energy of the system.If the matter is following try-nature property than dividing the frequency of E = hV in three parts. Arranging these in equation of (ii)-
Arranging these in equation of (ii)-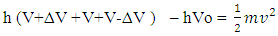
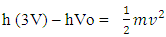
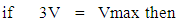
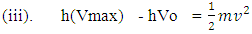 Now by Non-interactive mechanicsN+M = 0 (every system is the combination of Non-Intractable particle and Matter Field )Applying this in equation (iii).
Now by Non-interactive mechanicsN+M = 0 (every system is the combination of Non-Intractable particle and Matter Field )Applying this in equation (iii).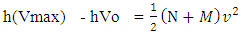
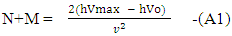 As according to the N-I mechanics equationsN+M = ±fp.o.f ( which is process of formation p.o.f )So equation –A1 becomes
As according to the N-I mechanics equationsN+M = ±fp.o.f ( which is process of formation p.o.f )So equation –A1 becomes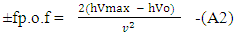 Now if we look the mass-energy relativistic relation is
Now if we look the mass-energy relativistic relation is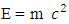 where c is speed of light or photonsAccording to Non-interactive mechanicsN+M = 0 where N is non-intractable particle and M is matter, this suggest the sum of N-I particle and Matter is equals to class zero particles. Also every system is the combination of Non-intractable particle and Matter.Applying this in mass-energy relation
where c is speed of light or photonsAccording to Non-interactive mechanicsN+M = 0 where N is non-intractable particle and M is matter, this suggest the sum of N-I particle and Matter is equals to class zero particles. Also every system is the combination of Non-intractable particle and Matter.Applying this in mass-energy relation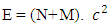 This equation can be represent as
This equation can be represent as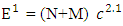
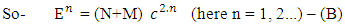 Here c are those particle which remains after the collision of positive and negative curve geometryMathematically, the velocity of light is
Here c are those particle which remains after the collision of positive and negative curve geometryMathematically, the velocity of light is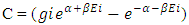 So equation –(B) becomes
So equation –(B) becomes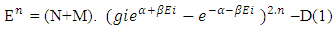 As N+M = ±fp.o.f
As N+M = ±fp.o.f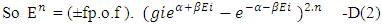 Now applying equation –A(1) and –A(2) in –D(1) and D(2)So-
Now applying equation –A(1) and –A(2) in –D(1) and D(2)So- 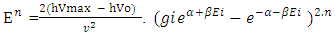 So three equations are
So three equations are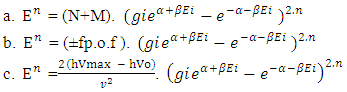 So the combined forms of these relations are
So the combined forms of these relations are
 The picture is showing the similar result as mentioned in the above equation so the relation could define particles their nature.
The picture is showing the similar result as mentioned in the above equation so the relation could define particles their nature. So the only misbalance in both states is the 1 mass holding state which is actually the cell holding particle entering in the matter field (M), so this gives the first positive curve geometry cell holding Particle is beyond the matter field, as entering in this cell non-intractable particle gain the field’s nature and qualities, before getting the physical form.“this gives the general idea that actions starts before they come to sense, or actions starts before their appearance seems physically”.(ii). The first particle enter in the matter field is positively rotating (R.H.R), so positive curve geometry is the prime geometry.The cell distribution formula for the non-interactive mechanics is
So the only misbalance in both states is the 1 mass holding state which is actually the cell holding particle entering in the matter field (M), so this gives the first positive curve geometry cell holding Particle is beyond the matter field, as entering in this cell non-intractable particle gain the field’s nature and qualities, before getting the physical form.“this gives the general idea that actions starts before they come to sense, or actions starts before their appearance seems physically”.(ii). The first particle enter in the matter field is positively rotating (R.H.R), so positive curve geometry is the prime geometry.The cell distribution formula for the non-interactive mechanics is 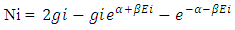 Now this equation suggesting that first particle which entering in the matter field, occupied the cell provided to it and it gives the nature of positively rotating under positive curve geometry.This gives the idea of first particle entering in matter field is positively rotating or following positive curve geometry.So if the field is generally define as –
Now this equation suggesting that first particle which entering in the matter field, occupied the cell provided to it and it gives the nature of positively rotating under positive curve geometry.This gives the idea of first particle entering in matter field is positively rotating or following positive curve geometry.So if the field is generally define as – According to Dirac’s particle –antiparticle theory these charge distribution should treated as matter and antimatter, as non-intractable particle enter in the positive curve geometry so-This gives the idea of “matter is more in universe correspond to it anti-matter”.(iii). Universe posses the mechanism of continuous creation and destruction-The supreme mechanics diagram states that 11th mass leaving and 12th mass holding states are co- bindingly creating the physical world’s phenomena.Here 11 mass leaving state continuously mass leaving it’s state which are under negative curve geometry
According to Dirac’s particle –antiparticle theory these charge distribution should treated as matter and antimatter, as non-intractable particle enter in the positive curve geometry so-This gives the idea of “matter is more in universe correspond to it anti-matter”.(iii). Universe posses the mechanism of continuous creation and destruction-The supreme mechanics diagram states that 11th mass leaving and 12th mass holding states are co- bindingly creating the physical world’s phenomena.Here 11 mass leaving state continuously mass leaving it’s state which are under negative curve geometry 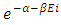 , while the 12th mass holding state continuously holding the mass states and with it the other 11 mass holding states are also attending the mass states.Where the similar in amount but different in rotation and property 11 mass leaving state is also present with negative curve geometrySo 11 mass holding state = 11 mass leaving stateWhere 1 one particle attending the mass field continuously holding the mass field.This give the continuous process of mechanisms creation and destruction where creation is prime.(iv). Every Physical particle is the combination of the N-i particle and Mass field (M)-Now generally the laws of physics are written as-
, while the 12th mass holding state continuously holding the mass states and with it the other 11 mass holding states are also attending the mass states.Where the similar in amount but different in rotation and property 11 mass leaving state is also present with negative curve geometrySo 11 mass holding state = 11 mass leaving stateWhere 1 one particle attending the mass field continuously holding the mass field.This give the continuous process of mechanisms creation and destruction where creation is prime.(iv). Every Physical particle is the combination of the N-i particle and Mass field (M)-Now generally the laws of physics are written as- now all the quantities are positive matter field’s and the intractable properties of (F, E, P) and their effects in physical world can be easily observe.By N-I mechanics this type of force is under positive curve geometry or in other words under positive matter field by the cell distribution formula
now all the quantities are positive matter field’s and the intractable properties of (F, E, P) and their effects in physical world can be easily observe.By N-I mechanics this type of force is under positive curve geometry or in other words under positive matter field by the cell distribution formula 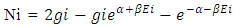 positive curve geometry is cell occupied geometry so for the matter field of positive curve geometry all the matter is the combination with it’s N-I particle orN + M = 0So the physical formula according to non-interactive mechanics is
positive curve geometry is cell occupied geometry so for the matter field of positive curve geometry all the matter is the combination with it’s N-I particle orN + M = 0So the physical formula according to non-interactive mechanics is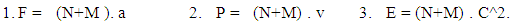 For N=0 or Non-Intractable particle is not present in matter field above equations become
For N=0 or Non-Intractable particle is not present in matter field above equations become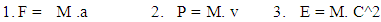
 This is mass energy equivalence law.Velocity of light
This is mass energy equivalence law.Velocity of light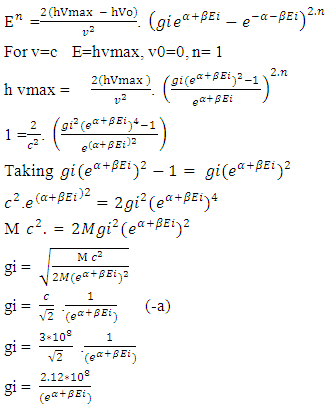
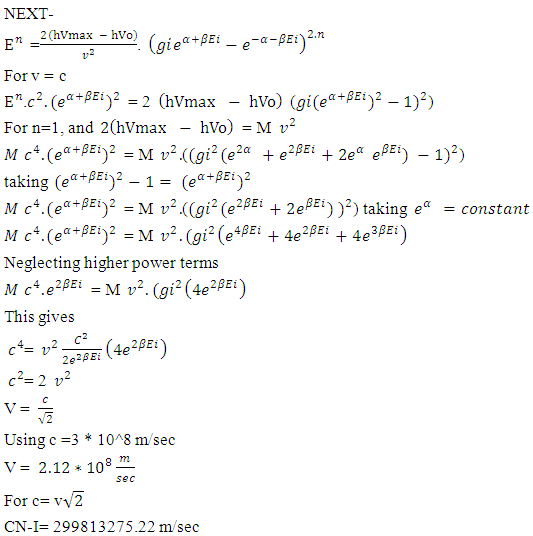 And the current velocity of light is c= 299792458m/secSo the difference is 20817.22 m/secThis gives particles faster than light and also termed as approximation of velocity of light.THE RELATIVISTIC CONDITION
And the current velocity of light is c= 299792458m/secSo the difference is 20817.22 m/secThis gives particles faster than light and also termed as approximation of velocity of light.THE RELATIVISTIC CONDITION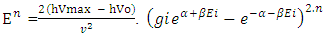 AS n=1 and
AS n=1 and 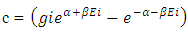
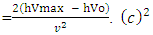 By photo electric effect
By photo electric effect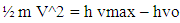 Applying this gives
Applying this gives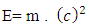 By non-interactive mechanicsN = -MMultiplying -1 on both sides gives
By non-interactive mechanicsN = -MMultiplying -1 on both sides gives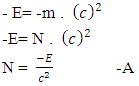 Later
Later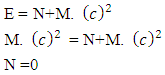 Putting in A gives
Putting in A gives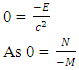 Equating both equation gives
Equating both equation gives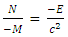 This gives
This gives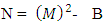 Next-
Next-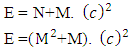 Squaring on both sides
Squaring on both sides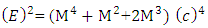 Neglecting higher power terms
Neglecting higher power terms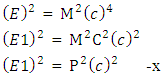 Then
Then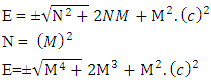 Neglecting higher power terms
Neglecting higher power terms Now squiring gives
Now squiring gives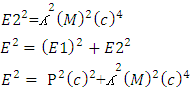 THEORTICLE AND EXPERIMENTAL PROOFS OF NON-INTERACTIVE MECHANICS-(i). Dirac’s theory of particle-antiparticle and positron as a proof -Every Electron posses both positive curve geometry’s dense energy and negative curve geometry’s spread energy or in other word every electron posses right handed and left handed rotation property . as by cell distribution formula for N-I particles
THEORTICLE AND EXPERIMENTAL PROOFS OF NON-INTERACTIVE MECHANICS-(i). Dirac’s theory of particle-antiparticle and positron as a proof -Every Electron posses both positive curve geometry’s dense energy and negative curve geometry’s spread energy or in other word every electron posses right handed and left handed rotation property . as by cell distribution formula for N-I particles 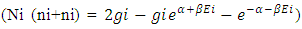 every N-I particle is comes in pair in which one is positive curve geometry particle and another is negative curve geometry particle this is same as ‘DIRAC’S ‘PARTICLE – ANTIPARTICLE’ THEORY ’, also justify the EXISTENSE OF POSITIVE ELECTRON ‘POSITRON’ WHICH IS SAME AS THEORTICLE AND EXPERIMENTAL RESULTS.(ii). Electrons posses both positive curve geometry’s ‘dense field energy and right hand rotation and also negative curve geometry’s spread field energy and it’s left hand rotation Which justify the positive and right hand rotating electron or ‘POSITRON’WHICH IS SAME AS THEORTICLE AND EXPERIMENTAL RESULTS.
every N-I particle is comes in pair in which one is positive curve geometry particle and another is negative curve geometry particle this is same as ‘DIRAC’S ‘PARTICLE – ANTIPARTICLE’ THEORY ’, also justify the EXISTENSE OF POSITIVE ELECTRON ‘POSITRON’ WHICH IS SAME AS THEORTICLE AND EXPERIMENTAL RESULTS.(ii). Electrons posses both positive curve geometry’s ‘dense field energy and right hand rotation and also negative curve geometry’s spread field energy and it’s left hand rotation Which justify the positive and right hand rotating electron or ‘POSITRON’WHICH IS SAME AS THEORTICLE AND EXPERIMENTAL RESULTS.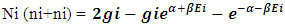 .2. A field quanta is the union of N-i particle and matter, according to the formula N+M=0.3. Energy and size of a Non-intractable particle is give by the equation
.2. A field quanta is the union of N-i particle and matter, according to the formula N+M=0.3. Energy and size of a Non-intractable particle is give by the equation 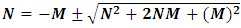 the equation shows same order as Masonic x-ray detection of nucleus radius
the equation shows same order as Masonic x-ray detection of nucleus radius 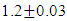 fm.This is also same as deuterons binding energy
fm.This is also same as deuterons binding energy 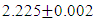 Mev.4. In the process of attending matter field N-I particles change into elementary particles like proton, electron, positron5. According to Non-interactive mechanics the movement of non intractable particles happens before it comes in the sense of physical observation.6. The laws of Physics where Mass is mentioned should improvised, it should written as “N+M” in place of only ‘M’, such as
Mev.4. In the process of attending matter field N-I particles change into elementary particles like proton, electron, positron5. According to Non-interactive mechanics the movement of non intractable particles happens before it comes in the sense of physical observation.6. The laws of Physics where Mass is mentioned should improvised, it should written as “N+M” in place of only ‘M’, such as 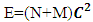 in above manuscript this relation satisfies the relativistic condition
in above manuscript this relation satisfies the relativistic condition 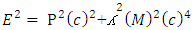 with the relation
with the relation 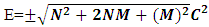 .7.Non-intractable particles are faster than the velocity of light, as the velocity of non-intractable particle is CN-I= 299813275.22 m/sec and current velocity of light is c= 299792458m/sec so Non-intractable particles are20817.22 m/sec faster than light.8. Every reaction of N-I particles in universe follows “Nishant Effect”, here the energy of N-i Particle follows tri-nature property, these energies are
.7.Non-intractable particles are faster than the velocity of light, as the velocity of non-intractable particle is CN-I= 299813275.22 m/sec and current velocity of light is c= 299792458m/sec so Non-intractable particles are20817.22 m/sec faster than light.8. Every reaction of N-I particles in universe follows “Nishant Effect”, here the energy of N-i Particle follows tri-nature property, these energies are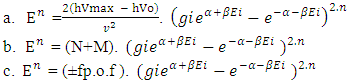 These relations satisfies the conditions ofi. Linear harmonic oscillator E=1/2 hvii. Plank’s radiation law E= hviii. Einstein mass-energy equivalence relation E= mc^2iv. Relativistic condition
These relations satisfies the conditions ofi. Linear harmonic oscillator E=1/2 hvii. Plank’s radiation law E= hviii. Einstein mass-energy equivalence relation E= mc^2iv. Relativistic condition 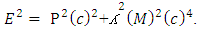 9. The structure of Nucleus and atom according to Non-Interactive Mechanics in manuscript shows same view as LIGO Experiment.
9. The structure of Nucleus and atom according to Non-Interactive Mechanics in manuscript shows same view as LIGO Experiment.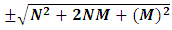 and creates the radius and binding energy of Nucleus and Atom The relation is given as
and creates the radius and binding energy of Nucleus and Atom The relation is given as 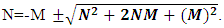 3. The Entering of N-I particles in matter field happens according to the process mentioned in Ramanujan Entering and the exchange of Non-Intractable particles happens according to the Ramanujan Effect.4. The disintegrated matter according to the formula
3. The Entering of N-I particles in matter field happens according to the process mentioned in Ramanujan Entering and the exchange of Non-Intractable particles happens according to the Ramanujan Effect.4. The disintegrated matter according to the formula 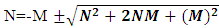 divides into two forms first is “dense energy field” which follows clockwise rotation and “spread energy field” which follows anticlockwise rotation in these energy fields Non-Intractable particles enter and follows the respective fields nature and gain energy in form of mass (as E is proportional m) due to this process particles like proton, electron, positrons forms.5. Non-intractable particles holds the nature to follow and fields properties such as spin, charge, mass, energy.6. After entering in matter field matter every Non-intractable particle follows Nishant Effect to gain matter field.
divides into two forms first is “dense energy field” which follows clockwise rotation and “spread energy field” which follows anticlockwise rotation in these energy fields Non-Intractable particles enter and follows the respective fields nature and gain energy in form of mass (as E is proportional m) due to this process particles like proton, electron, positrons forms.5. Non-intractable particles holds the nature to follow and fields properties such as spin, charge, mass, energy.6. After entering in matter field matter every Non-intractable particle follows Nishant Effect to gain matter field.  Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML