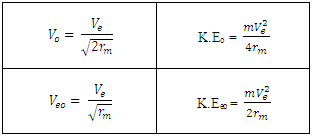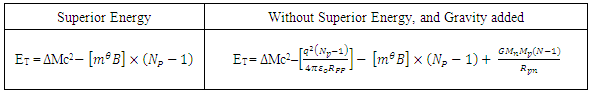Joshua Egbon
Department of Mechanical Engineering, Ambrose Alli University, Ekpoma, Nigeria
Correspondence to: Joshua Egbon, Department of Mechanical Engineering, Ambrose Alli University, Ekpoma, Nigeria.
| Email: |  |
Copyright © 2016 Scientific & Academic Publishing. All Rights Reserved.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/

Abstract
The purpose of this study is to bring out new approach for determining the distance between each nucleon in a nucleus, explain why nuclear force is a short range force, and why electrostatic force has greater range than magnetic force, predict the structure of Helium-4 nucleus through different tests, and combine four different energies equations—nuclear energy equation, magnetic potential energy equation, electrostatic energy equation, and gravitational energy equation to form one energy equation, which is the net energy of the nucleus.In this study mathematical models were used to arrive at various experimental results, and new equations were developed, which can be used to predict the net energy of the nucleus, the self energy of every nucleon, the energy released during nuclear fission, the size of the atom, and the contraction of the nucleons in any nucleus.
Keywords:
Nuclear Physics
Cite this paper: Joshua Egbon, Hypotheses on Nuclear Physics and Quantum Mechanics: A New Perspective, Journal of Nuclear and Particle Physics, Vol. 6 No. 1, 2016, pp. 10-23. doi: 10.5923/j.jnpp.20160601.03.
1. Introduction
Various attempts have been made in the past to determine the size of the nucleus (Geoff, 2010), as well as unify all the fundamental forces and elementary particles to be written in terms of a single field (Hubert, 2004).The great accomplishment by others in determining the radius of the proton, its magnetic moment and mass will be of tremendous benefit in this study (Mohr, 2011). The nuclear binding energy equation may not be used to predict the centre-to-centre distance between each proton and neutron in a nucleus; neither can the electrostatic energy equation account for the energy released in the fission of Uranium-235 (Gopal, 2010). Magnetic potential energy equation cannot be used to determine the energy of the revolving electron; and gravitational energy is the weakest of these forces in the nucleus.A proper understanding of these forces/energies acting in the nucleus in terms of their range and strength is needed for precise prediction to be made on the effect of these forces/energies within and outside the nucleus (Varadarajan, 2004). These forces which all act in the nucleus will be used in determining the centre-to-centre distance apart between each neutron and proton in the nucleus, the atomic radius of revolving electron, the energy released in the fission of Uranium-235, the net energy of every nucleus system, and the contraction of the nucleons which leads to a loss in mass in the nucleus.This study help bring together four different energies equations—nuclear energy equation, magnetic potential energy equation, electrostatic energy equation, and gravitational energy equation to form one energy equation, which is the net energy of the nucleus. In this study mathematical models were used to arrive at various experimental results (Billings, 2013), and new equations were developed, which can be used to predict the net energy of the nucleus, the self energy of every nucleon, the energy released during nuclear fission, the size of the atom, and the contraction of the nucleons in any nucleus
2. Test for the Structure of Helium-4 Nucleus
Fundamental Knowledge/Mathematical DerivationsSome basic knowledge of orbiting bodies in gravitational field is needed here. From gravitational law the velocity of a satellite around an orbit is given by: 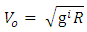 | (1.1) |
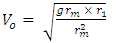 | (1.2) |
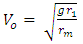 | (1.3) |
Where gi = acceleration due to gravity at that orbitg = gravity of the orbited body at its surface R = centre radius apart between orbited body and satellite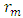 = Multiple of force producer radius to distance apart
= Multiple of force producer radius to distance apart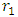 = force producer radius Escape velocity at any orbit,
= force producer radius Escape velocity at any orbit, 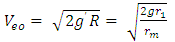 | (1.4) |
From 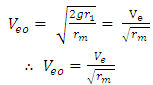 | (1.5) |
Ve-escape velocity at surface of force producerAlso, 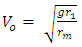 Which is
Which is 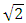 times less than Veo
times less than Veo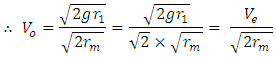 V0 – orbiting velocity round the earth
V0 – orbiting velocity round the earth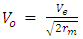 | (1.6) |
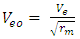 | (1.7) |
Kinetic energy of an orbiting body 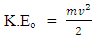 | (1.8) |
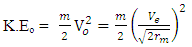 Where V = Vo and M- mass of orbiting body
Where V = Vo and M- mass of orbiting body 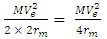 | (1.9) |
The least energy it will use to escape that orbit is 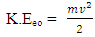 here V = Veo
here V = Veo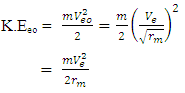 | (1.9.1) |
Table 1.1. Relationship between Vo, Veo, rm, K.Eo, and K.Eeo
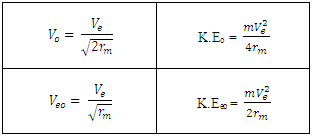 |
| |
|
When two bodies are almost of similar weight, it is impossible for one to orbit the other.When like poles of magnets are placed near each other, both repel themselves and escape at the least escape velocity around that orbit.If two magnets M1 and M2 of different poles are attracted to each other at a distance apart, M2 of different poles are attracted to spring balances at a distance apart, M2 will record more reading on the spring balance if its mass is less than M1. This means that M2 is more likely to move towards M1 at the velocity around M1 orbit.  | Figure 1.1. Extension of spring under magnetic field |
With this basic knowledge the nuclear binding energy can be studied.Nuclear force is a short range force (like magnetic force is short range) that exists between proton-proton, proton-neutron, and neutron-neutron.Nuclear energy is the energy required to split the nucleus of an atom into its component part. It is the binding energy. The protons of hydrogen combine to helium only if they have enough velocity to overcome each other’s mutual repulsion sufficiently to get within range of the strong nuclear attraction.The Potential Energy (P.E) of an object at any point from the centre of the earth is given by 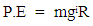 | (1.9.2) |
But 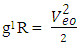
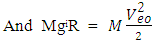 | (1.9.3) |
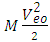 is the least energy it will use to escape that orbit.Therefore the P.E of any system is equal to the least energy needed to separate the system.For two magnets of like poles, the energy needed to separate them is equal to their P.E and the magnets will move at a velocity away from each other, which is equal to the escape velocity at that orbit.A body may be considered a system if no external force is acting on it, or if external force does not have effect on it. Total Energy in a system: the Binding EnergyConsider a system to be formed of N magnets having equal masses, and the distance between any two closest magnets is the same. The binding energy or P.E for all the bodies is the total energy used to hold them together.Total Binding energy
is the least energy it will use to escape that orbit.Therefore the P.E of any system is equal to the least energy needed to separate the system.For two magnets of like poles, the energy needed to separate them is equal to their P.E and the magnets will move at a velocity away from each other, which is equal to the escape velocity at that orbit.A body may be considered a system if no external force is acting on it, or if external force does not have effect on it. Total Energy in a system: the Binding EnergyConsider a system to be formed of N magnets having equal masses, and the distance between any two closest magnets is the same. The binding energy or P.E for all the bodies is the total energy used to hold them together.Total Binding energy 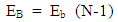 | (1.9.4) |
Where EB = total binding energyEb = binding energy between any two magnetN = total number of magnets 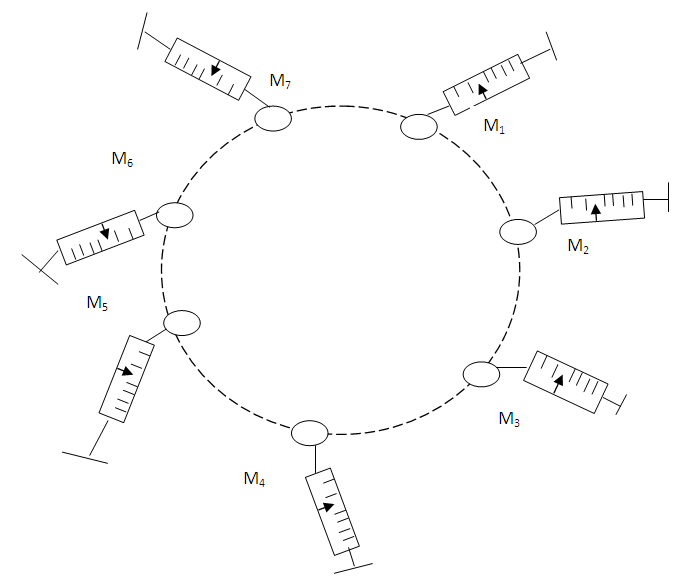 | Figure 1.2. Multiple magnets in a force field |
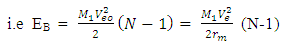 | (1.9.5) |
rm – multiple of radius of one magnet with the distance between the closest magnet Ve – escape velocity at r1Veo – escape velocity at r1 x rm = RThis basic knowledge will be used in dealing with the binding energy of various nucleuses of elements.A nucleus will be considered a close system since no external force is acting on it. The electrostatic force between revolving electrons do not affect the position of the nucleus because of the greater weight of the nucleus. In the nucleus system, the proton which has a mass slightly lesser than the neutron is used as the object because the force acting on it is the least force needed to separate the system.Fundamental knowledge of electrostatic potential energy is also required. The electrostatic potential energy between the electron and the proton if the electron is on the surface of the proton is: 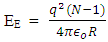 | (1.9.6) |
Where N- total number of charge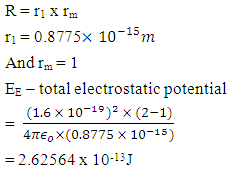
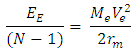 where Me – mass of electronThe escape velocity of electron at proton surface is
where Me – mass of electronThe escape velocity of electron at proton surface is 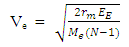 | (1.9.7) |
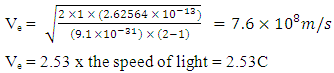 From Bohr’s theory on atomic model, the electron at the lowest energy level of a hydrogen atom has energy of 13.6eV (21.8 x 10-19J). This energy is the energy of the orbiting electron (E0)
From Bohr’s theory on atomic model, the electron at the lowest energy level of a hydrogen atom has energy of 13.6eV (21.8 x 10-19J). This energy is the energy of the orbiting electron (E0)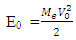 | (1.9.8) |
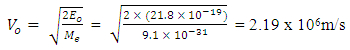 From
From 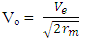
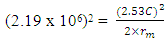
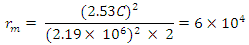
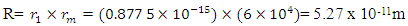 This is the centre radius between the orbiting electron and the proton in a hydrogen atom – or the radius of the hydrogen atom. Mathematical Models for Helium-4 StructureHelium-4 nucleus is extremely stable. To know the structure of this nucleus, some possible outcome of its structure will be subjected to two different tests:a. Atomic Radius Testb. Nuclear Fission (electromagnetic potential ) Energy TestP – ProtonN – Neutron Model i)
This is the centre radius between the orbiting electron and the proton in a hydrogen atom – or the radius of the hydrogen atom. Mathematical Models for Helium-4 StructureHelium-4 nucleus is extremely stable. To know the structure of this nucleus, some possible outcome of its structure will be subjected to two different tests:a. Atomic Radius Testb. Nuclear Fission (electromagnetic potential ) Energy TestP – ProtonN – Neutron Model i) 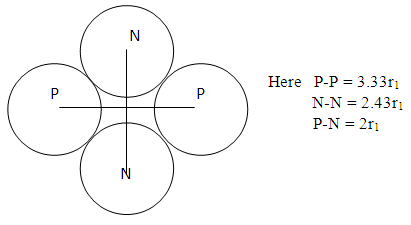 | Figure 2.1. Model I |
Model ii)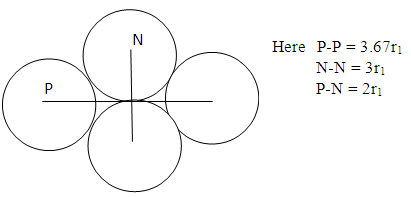 | Figure 2.2. Model II |
Model iii)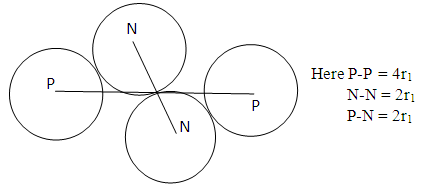 | Figure 2.3. Model III |
Model iv)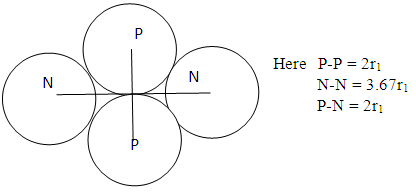 | Figure 2.4. Model IV |
Test A: Atomic Radius TestUsing Mercury as a case study:Mercury – N = 201; np = 80; nn = 121Where N - number of protons and neutrons in the nucleus np – number of protons in the nucleusnn – number of neutrons in the nucleus Atomic mass M2 = 200.9703023u; Lowest energy level or ground state of the electron = 10.4eV; empirical atomic radius Ra= 1.51 x 10-10m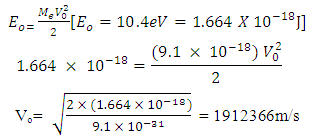 Atomic nucleus radius
Atomic nucleus radius 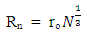 | (2.1) |
This formula is used for heavier nuclei (N>20); wherero = 1.2 – 1.5fm; and N- total number of protons and neutrons in the nucleus.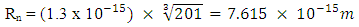
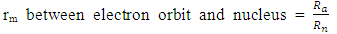 | (2.2) |
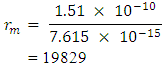 Test B: Nuclear Fission Energy TestIn nuclear fission, the absorption of a neutron by a heavy nuclide (e.g U-235) causes the nuclide to become unstable and break into light nuclides and additional neutrons. This positively charged light nuclide then repel, releasing electromagnetic potential energy.
Test B: Nuclear Fission Energy TestIn nuclear fission, the absorption of a neutron by a heavy nuclide (e.g U-235) causes the nuclide to become unstable and break into light nuclides and additional neutrons. This positively charged light nuclide then repel, releasing electromagnetic potential energy.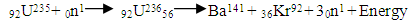 The fission of one atom of U-235 generates 202.5 MeV = 3.24 x10-11JThe Helium-4 model must meet these criterion or have values that are near rm = 19829 and Er = 3.24 x 10-11J(Where Er = energy released). Model ITest A: At rpp = 3.33r1 for the helium nucleus where rpp = p-p distance.Then from
The fission of one atom of U-235 generates 202.5 MeV = 3.24 x10-11JThe Helium-4 model must meet these criterion or have values that are near rm = 19829 and Er = 3.24 x 10-11J(Where Er = energy released). Model ITest A: At rpp = 3.33r1 for the helium nucleus where rpp = p-p distance.Then from 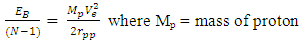 Helium-4 has atomic mass of 4.00260325415U = 6.64648 x10-27kgActual mass of 2 protons + 2 electrons + 2 neutrons = 6.697 x 10-27kg
Helium-4 has atomic mass of 4.00260325415U = 6.64648 x10-27kgActual mass of 2 protons + 2 electrons + 2 neutrons = 6.697 x 10-27kg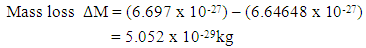 Total Binding Energy
Total Binding Energy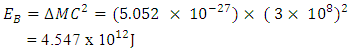
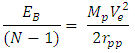 Number of nucleons in Helium-4 is 4
Number of nucleons in Helium-4 is 4 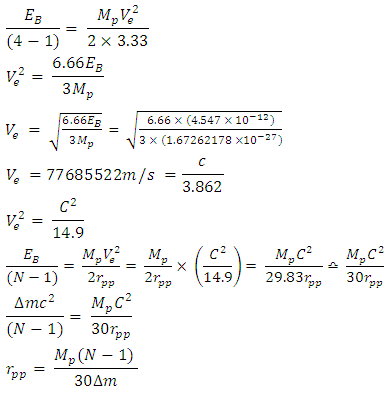 | (2.3) |
Using this formula, the distance between any two closest protons in a mercury nucleus can be determined. Actual mass of 80 protons + 80 electrons + 121 neutrons in a Mercury–201 atom = 1.338097424 x 10-25 + 7.28 x10-29+ 2.026662094 x 10-25M1 = 3.365487518 x 10-25kgActual mass of mercury–201 =200.9703023U = 3.3372 x 10-25kg 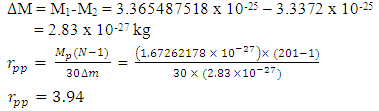 Radius between any two closest proton in a mercury-201nucleus is given by
Radius between any two closest proton in a mercury-201nucleus is given by 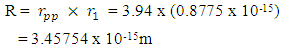 If an electron is brought to the mercury nucleus, and placed 3.45754 x 10-15m away from any proton, thereby increasing the total number of charge of the nucleus, then the electrostatic energy of the nucleus will be:
If an electron is brought to the mercury nucleus, and placed 3.45754 x 10-15m away from any proton, thereby increasing the total number of charge of the nucleus, then the electrostatic energy of the nucleus will be: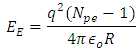 Where Npe – total number of protons + 1 electron added to the nucleus
Where Npe – total number of protons + 1 electron added to the nucleus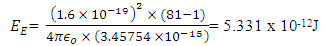 Energy between a proton and this electron:
Energy between a proton and this electron: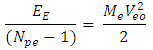 Velocity the electron will use to escape from this distance of 3.45754 x10-15m from the closest proton:
Velocity the electron will use to escape from this distance of 3.45754 x10-15m from the closest proton: 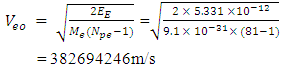 Since this velocity is the velocity at the nucleus, it can be regarded as the escape velocity Ve when compared to that used by the electron to orbit the nucleus 1.51 x 10-10m away.
Since this velocity is the velocity at the nucleus, it can be regarded as the escape velocity Ve when compared to that used by the electron to orbit the nucleus 1.51 x 10-10m away. 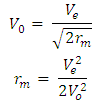 Recall that the velocity of the orbiting electron in Mercury–201 atom is 1912366m/s
Recall that the velocity of the orbiting electron in Mercury–201 atom is 1912366m/s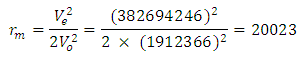
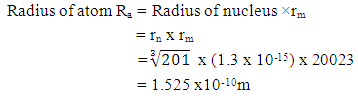 This compares well with the known 1.51 x 10-10m (empirical radius)Test B: Nuclear fission (Electromagnetic potential) Energy TestEnergy released = Electromagnetic potential energy in nucleusThe nucleus in question here is Uranium–235, whose isotope mass number is 235.0439299U = 3.903 x 10-25kg, atomic number = 92; number of neutron = 143Actual mass of 92 protons + 92 electrons + 143 neutronsM1 = 3.9348 x 10-25kg Mass loss
This compares well with the known 1.51 x 10-10m (empirical radius)Test B: Nuclear fission (Electromagnetic potential) Energy TestEnergy released = Electromagnetic potential energy in nucleusThe nucleus in question here is Uranium–235, whose isotope mass number is 235.0439299U = 3.903 x 10-25kg, atomic number = 92; number of neutron = 143Actual mass of 92 protons + 92 electrons + 143 neutronsM1 = 3.9348 x 10-25kg Mass loss 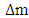 = M1-M2 = (3.9348 x 10-25) – (3.903 x10-25)= 3.179535 x 10-27Kg
= M1-M2 = (3.9348 x 10-25) – (3.903 x10-25)= 3.179535 x 10-27Kg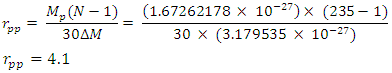 Radius between any two closest protons in the nucleus
Radius between any two closest protons in the nucleus 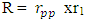
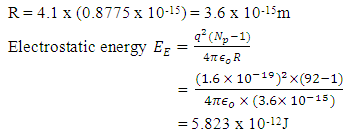 Magnetic potential Energy
Magnetic potential Energy 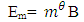 | (2.4) |
Where 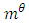 = magnetic moment of a proton, which is equal to 1.410606743 x 10-26J/T
= magnetic moment of a proton, which is equal to 1.410606743 x 10-26J/T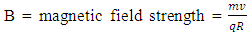 | (2.5) |
From electrostatic energy, Vat distance R is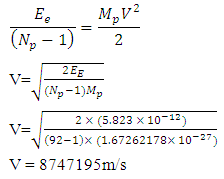 Magnetic fields are produced by electric currents. The protons in a nucleus has magnetic properties because of the charge they carry. The electrostatic energy between the protons will cause them to move away from each other at a velocity (V which is equal to 8747195m/s for the uranium-235); thereby generating magnetic energy.The magnetic field strength
Magnetic fields are produced by electric currents. The protons in a nucleus has magnetic properties because of the charge they carry. The electrostatic energy between the protons will cause them to move away from each other at a velocity (V which is equal to 8747195m/s for the uranium-235); thereby generating magnetic energy.The magnetic field strength 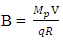
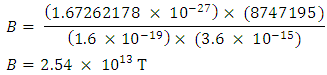 Since each proton repels the other 91 protons in the nucleus, the magnetic potential energy for the nucleus is given by
Since each proton repels the other 91 protons in the nucleus, the magnetic potential energy for the nucleus is given by 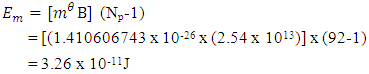 This compares well with the 3.24 x 10-11J energy released during fission of Uranium-235ResultsTable of Result for all the Models:
This compares well with the 3.24 x 10-11J energy released during fission of Uranium-235ResultsTable of Result for all the Models:Table 2.1. Results for all models
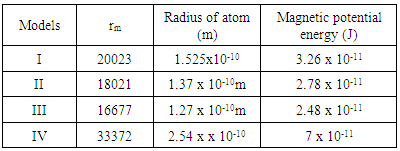 |
| |
|
Expected result: rm = 19829; Ra = 1.51 x 10-10m, and Er = 3.24 x 10-11J ConclusionsFrom the various models of Helium-4 Nucleus Model I compares best with the known results of rm = 19829, Ra = 1.51 x 10-10m, and Er = 3.24 x 10-11 JFrom Model I Test II, it can be said that the energy released is the magnetic potential energy and not electrostatic potential energy or an addition of both. Description of Model I: (Helium-4 Nucleus)v The centre distance between the two proton in a Helium-4 nucleus is 3.33 x the radius of a proton v The distance between any proton and the closest neutron is 2 x the radius of the protonv The distance between the two neutrons is 2.43 x the radius of a proton v The binding energy of Helium-4 nucleuses is 4.547 x 10-12Jv The electrostatic potential energy is 7.885 x 10-14Jv The magnetic potential energy is 4.9 x 10-13Jv The centre distance between the farthest proton and neutron is 2 x the radius of a proton From this model an equation for the N-N centre distance as well as the P-N centre distance can be written N-N: Where Mn- mass of neutron N- number of nucleons =4 rnn – 2.43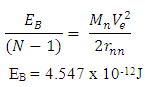
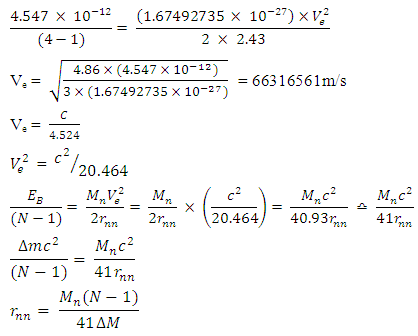 | (2.6) |
P-N:Where Mp- mass of ProtonN- number of nucleus rpn – 2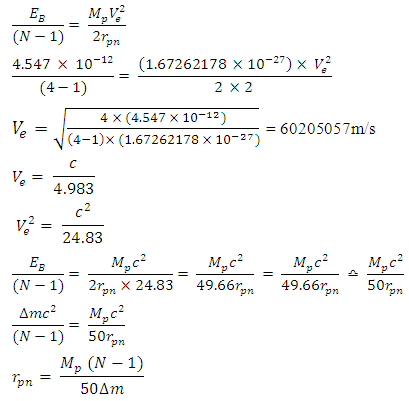 | (2.7) |
Table 2.2. Bond type and the binding energy of any nucleus
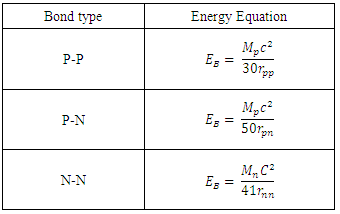 |
| |
|
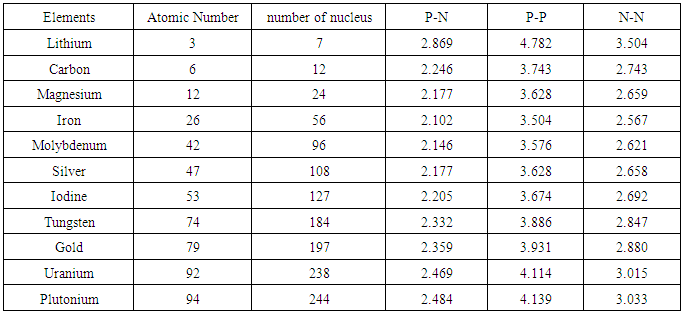
Centre–to–Centre Radii of the Nucleons of Some ElementsUsing the formula 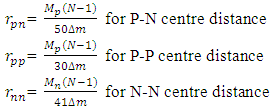 Note the distance R = r1 x rmwhere rm = rpp or rpn or rnnFrom the above table, it can be seen that P-N, P-P and N-N are closest at Iron–56. This means Iron-56 from the table above has the greatest bond between any two nucleons in the nucleus.
Note the distance R = r1 x rmwhere rm = rpp or rpn or rnnFrom the above table, it can be seen that P-N, P-P and N-N are closest at Iron–56. This means Iron-56 from the table above has the greatest bond between any two nucleons in the nucleus.
3. Hypothesis on Nuclear Forces
The binding energy between any two nucleons is given by 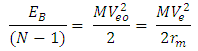 Where m = mass of the smaller nucleon and
Where m = mass of the smaller nucleon and 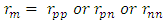 From Tab 2.3 one can look for the binding energy for each nucleus and find the relationship between them. It can be seen from the table that
From Tab 2.3 one can look for the binding energy for each nucleus and find the relationship between them. It can be seen from the table that  is increasing. A good relationship between the binding energy between any two nucleons in a nucleus and the distance apart will be used to formulate a new equation.Mathematical Models:i) Magnesium–24 has binding energy between any two closest proton and neutron
is increasing. A good relationship between the binding energy between any two nucleons in a nucleus and the distance apart will be used to formulate a new equation.Mathematical Models:i) Magnesium–24 has binding energy between any two closest proton and neutron 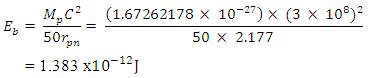 ii) Molybdenum–96 has binding energy between any two closest proton and neutron
ii) Molybdenum–96 has binding energy between any two closest proton and neutron 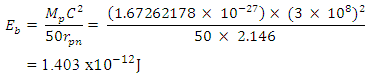 iii) Uranium–238 has binding energy between any two closest proton and neutron
iii) Uranium–238 has binding energy between any two closest proton and neutron 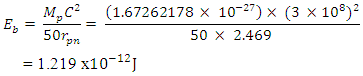
Table 2.3. Centre-to-centre radii of the nucleons of some elements
 |
| |
|
Relationship: 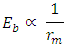
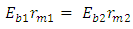 Mathematical Model:What is the centre-centre multiple distance for Iron-56 if the binding energy between any proton and neutron in an Iron-56 nucleus is 1.432 x 10-12J. (Take binding energy of Magnesium-24 and centre–to–centre multiple of its closest proton and neutron to be 1.383 x 10-12J and 2.177 respectively.)
Mathematical Model:What is the centre-centre multiple distance for Iron-56 if the binding energy between any proton and neutron in an Iron-56 nucleus is 1.432 x 10-12J. (Take binding energy of Magnesium-24 and centre–to–centre multiple of its closest proton and neutron to be 1.383 x 10-12J and 2.177 respectively.)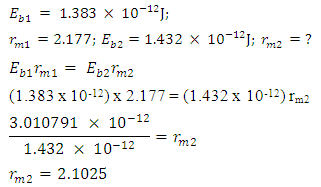 This can be compared with 2.102 which is in the table. Mathematical Model:An unknown element has binding energy between two of its closest nucleons as
This can be compared with 2.102 which is in the table. Mathematical Model:An unknown element has binding energy between two of its closest nucleons as 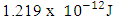 , and the centre distance between the two nucleons is 2.469. What will be the binding energy between any two closest nucleons of Molybdenum-96, whose centre–to–centre distance multiple is 2.146
, and the centre distance between the two nucleons is 2.469. What will be the binding energy between any two closest nucleons of Molybdenum-96, whose centre–to–centre distance multiple is 2.146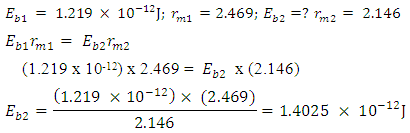 This compares well with the 1.403 x
This compares well with the 1.403 x 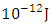 of the Molybdenum–96 Conclusion:From the above, it can be concluded that the binding energy between any two nucleons is inversely proportional to their distance apart
of the Molybdenum–96 Conclusion:From the above, it can be concluded that the binding energy between any two nucleons is inversely proportional to their distance apart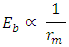 Also the total binding energy in any nucleus is given byEB = Eb (N-1)Energy = force x Distance = FRHypothesis on Nuclear Forces states that The force of attraction between any two nucleons held by nuclear forces, separated a distance R is proportional to the product of their masses and inversely proportional to the square root of their distance apart.
Also the total binding energy in any nucleus is given byEB = Eb (N-1)Energy = force x Distance = FRHypothesis on Nuclear Forces states that The force of attraction between any two nucleons held by nuclear forces, separated a distance R is proportional to the product of their masses and inversely proportional to the square root of their distance apart. 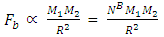 | (3.1) |
Where NB – nuclear constant, and varies for P-P, P-N and N-N 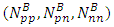 Energy is needed to bring a mass from infinity to the point in question, R.
Energy is needed to bring a mass from infinity to the point in question, R.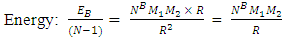 | (3.2) |
Recall that it was earlier stated that 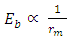 This present itself in a new form as:
This present itself in a new form as: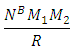 where
where 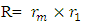 Self Energy of Every Nucleon
Self Energy of Every Nucleon 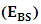 This is the self potential of every nucleon, and it is given by
This is the self potential of every nucleon, and it is given by 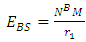 | (3.3) |
Where r1= radius of the nucleon Using Helium-4 which is a very stable nucleus as a model, NB can be gotten.For P-P: Helium-4 Rpp = r1 x rpp = (0.8775 x 10-15) x (3.33) = 2.922075 x 10-15m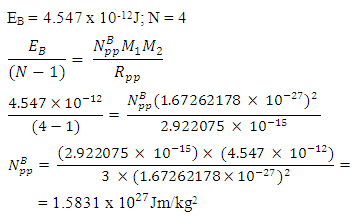
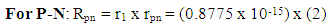
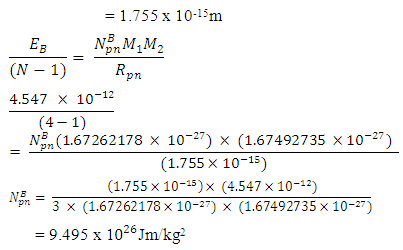
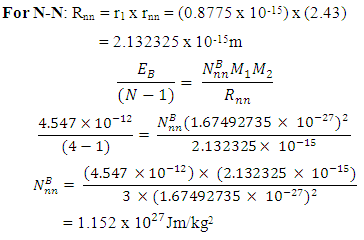 The nuclear force hypothesis when N> 2 for P-P, P-N and N-N
The nuclear force hypothesis when N> 2 for P-P, P-N and N-N 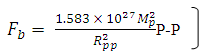 | (3.4) |
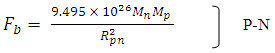 | (3.5) |
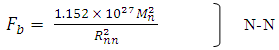 | (3.6) |
To know the energy between any two P-P or P-N or N-N, one multiply by R, so that 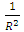 becomes
becomes 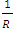 The total binding energy EB of any nucleus is given by:
The total binding energy EB of any nucleus is given by: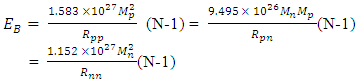 Mathematical Model: What is the centre-to-centre distance between any two closest neutrons in Tungsten–184 nucleus? Binding energy of Tungsten nucleus is 2.3631 x 10-10J. From the hypothesis of nuclear forces, when N>2,
Mathematical Model: What is the centre-to-centre distance between any two closest neutrons in Tungsten–184 nucleus? Binding energy of Tungsten nucleus is 2.3631 x 10-10J. From the hypothesis of nuclear forces, when N>2, 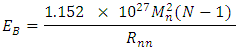

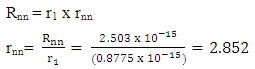 This compares well with the 2.847 that is in Tab 2.3.
This compares well with the 2.847 that is in Tab 2.3.
4. Hypothesis of Superior Forces / Energy
A charged particle at rest experiences a force in an electric field, but none in a magnetic field. A magnetic field doesn’t speed up or slow down a particle: because it doesn’t act on the parallel component of velocity, it only acts on the perpendicular component of velocity, so it can change the particle’s direction.Two instances can be sited:i. A magnet placed near a beam of high velocity electrons moving in a straight line, causes the electrons to move in a circular path without altering the velocity of the electrons ii. Planets are caused to orbit the sun because of the sun’s magnetic field. The forces of the revolving planets are not altered by the magnetic field, but only the gravitational force is considered.Added to these, electrons revolve round the nucleus under electrostatic force. The magnetic field that exist at the atomic level only cause the electron to move in circular path without slowing or increasing the velocity of the electron.It was earlier proved that the energy released during nuclear fission of Uranium–235 is magnetic potential energy and not the small electrostatic potential energy which is 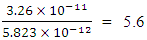 times smaller than the magnetic potential energy in the nucleus.Neither is the energy released an addition of the magnetic and electrostatic potential energy.In fact, the above three examples shows that the force of attraction on a revolving body is not a sum of the electrical and magnetic force or magnetic and gravitational force. Mathematical Models to Prove that the Magnetic Potential Energy is Dominant than the Electrical Energy at the NucleusTo prove why the magnetic field is dominant at the nucleus level, a simple nucleus (Hydrogen) shall be tested mathematically:Hydrogen: N = 1, proton radius = r1= 0.8775 x 10-15m, radius of atom Ra = 5.27 x 10-11m If a proton is placed near the proton (nucleus) of a hydrogen atom, at 2r1 away, then the electrostatic force of attraction will be
times smaller than the magnetic potential energy in the nucleus.Neither is the energy released an addition of the magnetic and electrostatic potential energy.In fact, the above three examples shows that the force of attraction on a revolving body is not a sum of the electrical and magnetic force or magnetic and gravitational force. Mathematical Models to Prove that the Magnetic Potential Energy is Dominant than the Electrical Energy at the NucleusTo prove why the magnetic field is dominant at the nucleus level, a simple nucleus (Hydrogen) shall be tested mathematically:Hydrogen: N = 1, proton radius = r1= 0.8775 x 10-15m, radius of atom Ra = 5.27 x 10-11m If a proton is placed near the proton (nucleus) of a hydrogen atom, at 2r1 away, then the electrostatic force of attraction will be 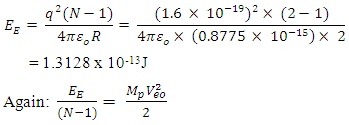 The escape velocity of this proton is
The escape velocity of this proton is 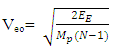
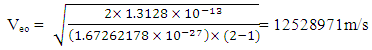 Also from
Also from 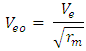 Note: From equation (2.2)
Note: From equation (2.2) 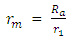 At 2r1, Veo = 12528971m/s is taken as the escape velocity Ve, so that
At 2r1, Veo = 12528971m/s is taken as the escape velocity Ve, so that 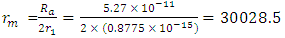
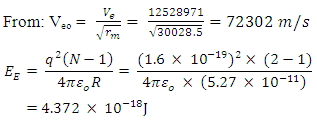 The Magnetic Potential Energy at both points
The Magnetic Potential Energy at both points 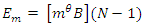 Where
Where 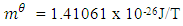
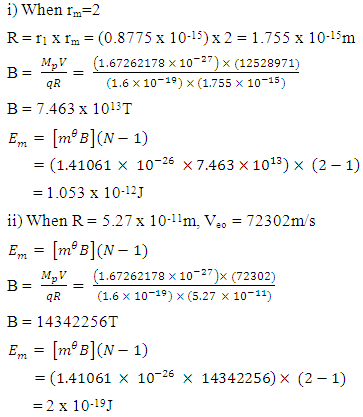 Results:EE at 1.755 x 10-15m = 1.3128 x 10-13 Jand at 5.27 x 10-11m = 4.372 x 10-18JEm at 1.755 x 10-15 = 1.053 x 10-12Jand at 5.27 x 10-11m = 2 x 10-19JConclusion: It is seen that the magnetic potential energy is greater than the electrostatic potential energy at the nucleus level, but at the atomic (radius) level the electrical energy is greater than the magnetic potential energy. Hypothesis of Superior Forces/Energystates: The potential or kinetic energy possessed by a body under a non–contact (electric, magnetic, gravitational or nuclear) field is a measure of the superior force field. Explanation: Beyond the atomic level magnetic force brings about bending effect, whereas gravitational and electrostatic force causes continuous movement. Net Energy in the NucleusTo know the net forces acting on any nucleus, it is assumed that the hypothesis of superior forces does not hold.Next, the forces (or total force) acting on the nucleus is divided into two—attracting and repulsive forces.The net force on the nucleus system is therefore
Results:EE at 1.755 x 10-15m = 1.3128 x 10-13 Jand at 5.27 x 10-11m = 4.372 x 10-18JEm at 1.755 x 10-15 = 1.053 x 10-12Jand at 5.27 x 10-11m = 2 x 10-19JConclusion: It is seen that the magnetic potential energy is greater than the electrostatic potential energy at the nucleus level, but at the atomic (radius) level the electrical energy is greater than the magnetic potential energy. Hypothesis of Superior Forces/Energystates: The potential or kinetic energy possessed by a body under a non–contact (electric, magnetic, gravitational or nuclear) field is a measure of the superior force field. Explanation: Beyond the atomic level magnetic force brings about bending effect, whereas gravitational and electrostatic force causes continuous movement. Net Energy in the NucleusTo know the net forces acting on any nucleus, it is assumed that the hypothesis of superior forces does not hold.Next, the forces (or total force) acting on the nucleus is divided into two—attracting and repulsive forces.The net force on the nucleus system is therefore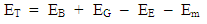 | (4.1) |
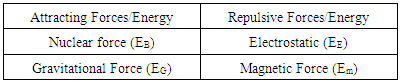
Table 4.1. Division of Forces in a Nucleus
 |
| |
|
But when compared to the other forces/energy gravity is very weak at the atomic level. Example: The gravitational energy between the protons in a Plutonium-94 nucleus is: This is negligible when compared with the electrostatic potential energy, which is:
This is negligible when compared with the electrostatic potential energy, which is: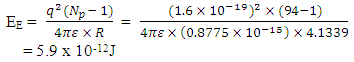 The new equation for the net energy then becomes:
The new equation for the net energy then becomes: 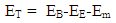 | (4.2) |
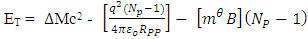 | (4.3) |
But 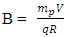 and Np = number of protons in nucleus
and Np = number of protons in nucleus 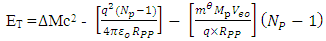 | (4.4) |
But if the hypothesis of superior energy is put into consideration, the superior repulsive energy is Em. Then the net Energy becomes: 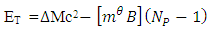 | (4.5) |
Summary of Net energy acting on nucleus with or without considering the Hypothesis of Superior EnergyTable 4.2. Net energy equation, with and without superior energy
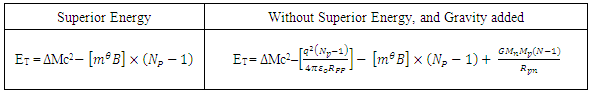 |
| |
|
5. Hypothesis on Nucleons Contraction, Mass Loss and Binding Energy
The protons of hydrogen combine to helium only if they have enough velocity to overcome each other’s mutual repulsion sufficiently to get within range of the strong nuclear attraction. If two or more nucleons are to be brought together to be at a distance apart from each other, from Lorentz transformation, if they are brought together at a great speed, which can be compared with the speed of light c, then the length of the particles will appear to be less than its original length. Mathematical ModelUsing Lithium-7 as a case study:EB = 6.2961 x 10-12J, Rpn = 2.5175475 x 10-15m, rpn = 2.869,r1 = 0.8775x10-15m The potential (nuclear) energy holding the protons and neutrons in Lithium-7 nucleus is equal to the Kinetic energy at which they will separate. 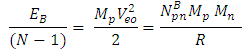 From Lorentz transformation, new length due to V is given by the equation:
From Lorentz transformation, new length due to V is given by the equation: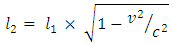 For the proton and neutron which has escape velocity compared to C, there will be a change in their radius, so that the new radius will be:
For the proton and neutron which has escape velocity compared to C, there will be a change in their radius, so that the new radius will be: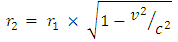 Where V= escape velocity of the nucleon r1 = original radius of the nucleon (proton or neutron)From
Where V= escape velocity of the nucleon r1 = original radius of the nucleon (proton or neutron)From 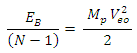
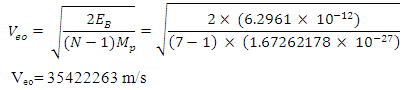 The new radius of the proton will be
The new radius of the proton will be 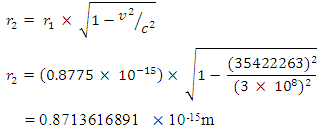
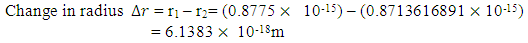 But the total self energy of every nuclear in the nucleus is constant provided no external energy disturb or is acting on the system. The self energy for one nucleon (proton):
But the total self energy of every nuclear in the nucleus is constant provided no external energy disturb or is acting on the system. The self energy for one nucleon (proton): 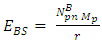 Before change in radius = r1After change in radius = r2Before change in radius
Before change in radius = r1After change in radius = r2Before change in radius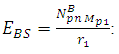 From equation (3.5) when N>2,
From equation (3.5) when N>2, 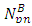 = 9.495 x 1026Jm/Kg2
= 9.495 x 1026Jm/Kg2 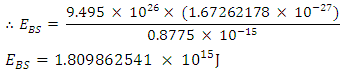 From Lorentz transformation there will be change in radius of the nucleus. This change in radius will lead to a change in mass for the self energy to remain constant since no external force is acting on the system. So that
From Lorentz transformation there will be change in radius of the nucleus. This change in radius will lead to a change in mass for the self energy to remain constant since no external force is acting on the system. So that 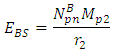
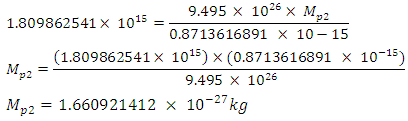 If (Mp1- Mp2) is the mass loss between the proton and neutron, total mass loss is given by
If (Mp1- Mp2) is the mass loss between the proton and neutron, total mass loss is given by 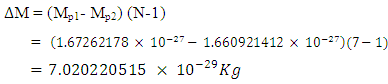
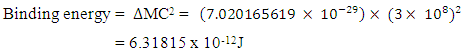 This is in agreement with the accepted value 6.2960508 x 10-12JIt is represented thus:
This is in agreement with the accepted value 6.2960508 x 10-12JIt is represented thus: R = uncharged, but r1 and r2 changes
R = uncharged, but r1 and r2 changes
6. Reasons for Nuclear force Being Short Range
Mathematical ModelsUsing Mercury-201 as a case study, change in mass is 2.83x10-27kg.From equation (2.7) centre-centre radius apart between a proton and neutron in the nucleus is given by: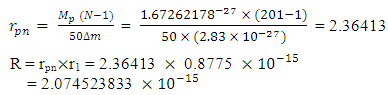 Mercury-201 has its electron lowest energy level at 1.51 x 10-10m which is 19829 x the radius of the nucleus
Mercury-201 has its electron lowest energy level at 1.51 x 10-10m which is 19829 x the radius of the nucleus 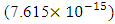 If a neutron is brought to the Mercury nucleus, and placed 2.074523833
If a neutron is brought to the Mercury nucleus, and placed 2.074523833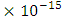 m away from any proton, thereby increasing the mass of the nucleus, then the nuclear energy of the nucleus will be:
m away from any proton, thereby increasing the mass of the nucleus, then the nuclear energy of the nucleus will be: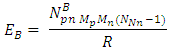 Where NNn--is the sum of the nucleons in the nucleus and the neutron added to it
Where NNn--is the sum of the nucleons in the nucleus and the neutron added to it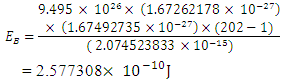 Energy between a proton and this neutron added to the nucleus:
Energy between a proton and this neutron added to the nucleus: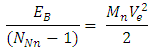 Ve is the velocity the added neutron will use to escape from the nucleus to
Ve is the velocity the added neutron will use to escape from the nucleus to 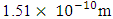 away from the centre of the nucleus, which is the region with the lowest energy level of the electron.
away from the centre of the nucleus, which is the region with the lowest energy level of the electron.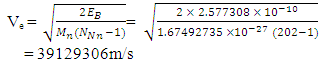 But
But 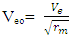 Recall that the radius multiple rm, between Mercury-201 nucleus and its empirical atomic radius is 19829Therefore,
Recall that the radius multiple rm, between Mercury-201 nucleus and its empirical atomic radius is 19829Therefore, 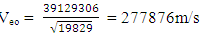 New radius of the neutron at a distance of
New radius of the neutron at a distance of 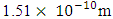 will be:
will be: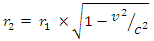
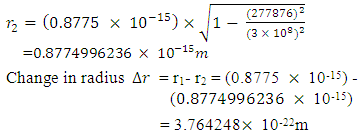 To know the mass loss, we first find the self potential energy:
To know the mass loss, we first find the self potential energy: 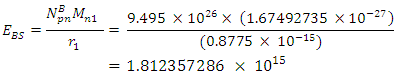 Also
Also 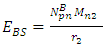
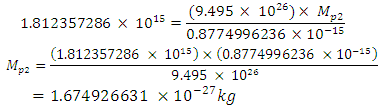
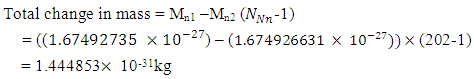
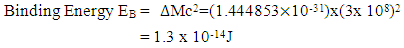 Solving for
Solving for 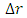 and
and 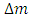 when the added neutron is
when the added neutron is 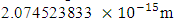 away from a proton in the nucleus:Recall that the escape velocity at this point is 39129306m/s.From Lorentz Transformation,
away from a proton in the nucleus:Recall that the escape velocity at this point is 39129306m/s.From Lorentz Transformation, 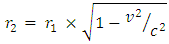
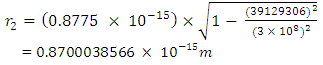
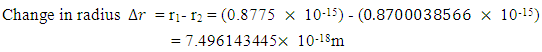 To know the mass loss, we first find the self potential energy:
To know the mass loss, we first find the self potential energy: 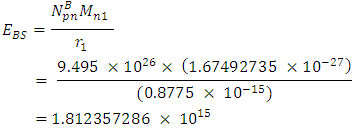 Also
Also 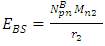
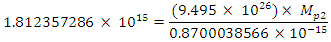
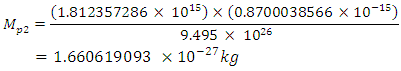
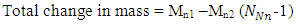
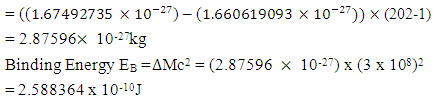 This binding energy is in agreement with the
This binding energy is in agreement with the 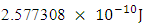 earlier gottenResults
earlier gottenResultsTable 5.1. Change in mass, radius and velocity
 |
| |
|
ConclusionsFrom Lorentz transformation:i) When V is very small as compared to c, V2/c2 will be negligible in comparison to unityTherefore, M1=M2 and r1=r2ii) When V is comparable to c, then 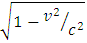 will bring about a considerable change in mass and radius Therefore M1> M2 and r1> r2For two or more nucleons to be held by nuclear energy, they must be brought under high velocity that is, they will have enough velocity to overcome each other’s repulsion (when there is more than one proton) - There must be a considerable change in mass- There must be a considerable change in radius of the nucleons- The least velocity at which they will be separated after they are joined together, must be comparable to the speed of light From the table of result above, it can be seen that the loss in mass, change in velocity and radius of the neutron when it is
will bring about a considerable change in mass and radius Therefore M1> M2 and r1> r2For two or more nucleons to be held by nuclear energy, they must be brought under high velocity that is, they will have enough velocity to overcome each other’s repulsion (when there is more than one proton) - There must be a considerable change in mass- There must be a considerable change in radius of the nucleons- The least velocity at which they will be separated after they are joined together, must be comparable to the speed of light From the table of result above, it can be seen that the loss in mass, change in velocity and radius of the neutron when it is 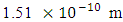 away is very small when compared to when it is
away is very small when compared to when it is 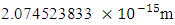 from the nearest proton.
from the nearest proton.
7. Discussion: A New Perspective of the Nucleus
It was earlier said that nucleons contract under nuclear force and this lead to a change in mass in order to balance the self energy (potential) of every nucleon in a nucleus. The greater the nuclear binding energy the greater will be the contraction, as well as the loss in mass. The further apart the nucleons are from each other the less loss in mass, as well as the contraction of the nucleons. If the contracted nucleons are separated outside the nuclear field, they may never regain their original radius. Thus: i) The centre distance between any two closest nucleons may be unchanged, whereas their radii may change ii) The nuclear self potential of any nucleon in a nucleus system is constant.
Physical Constant Used
To a good approximate, below are some constant used (all units are in S.I) Proton Mass = 1.67262178 X 10-27kgProton Charge radius = 0.8775X10-15mProton Magnetic Moment = 1.410606743 X 10-26J/TProton Charge = 1.6X10-19CNeutron radius = 0.8775 X 10-15mElectron charge = 1.6 X 10-19CPlanck Constant = 6.626 X 10-34JSNeutron mass = 1.67492735 X 10-27kgElectron Mass = 9.1 X 10-31KgAtomic Mass Unit = 1.66053892 X 10-27KgVacuum Permittivity 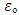 = 8.854 X 10-12F/mGravitational Constant = 6.7 X 10-11Nm2/kg2
= 8.854 X 10-12F/mGravitational Constant = 6.7 X 10-11Nm2/kg2
References
| [1] | RK Gaur, S.L. Gupta (1981): Engineering Physics Dhanpat Rai publications, 8th Edition Chapter 6, 25, 34, 43, 47, 48, 55, 56, 57, 61-64. |
| [2] | M. Nelkon (1977): Principles of Physics Hart-Davis Educational Limited, 7th Edition Chapter 35. |
| [3] | Osei Yaw Ababio: New School Chemistry Chapter 29 |
| [4] | www.cyberphysics.co.uk/Q&A/KS5/magneticFields/Q2ANS.html |
| [5] | en.m.wikibooks.org/wiki/A-level_Physics_(Advancing_Physics)/Binding_Energy/Worked_Solutions |
| [6] | en.m.wikipedia.org/wiki/Alpha_particle |
| [7] | en.m.wikipedia.org/wiki/Atomic_nuclues |
| [8] | en.m.wikipedia.org/wiki/Atomic_radii_of_the_elements_(data_page) |
| [9] | en.m.wikipedia.org/wiki/Atomic_radius#Empirically_measured_atomic_radii |
| [10] | en.m.wikipedia.org/wiki/Binding_energy |
| [11] | en.m.wikipedia.org/wiki/Charge_radius |
| [12] | en.m.wikipedia.org/wiki/Deuterium |
| [13] | www.physicsclassroom.com/class/circuits/lesson-1/Electric-Potential |
| [14] | en.m.wikipedia.org/wiki/Electrostatic_potential |
| [15] | hyperphysics.phy_astr.gsu.edu/hbase/electric/elepe.html |
| [16] | en.m.wikipedia.org/wiki/Electric_potential_energy |
| [17] | en.m.wikipedia.org/wiki/Electromagnetic_interaction |
| [18] | en.m.wikipedia.org/wiki/Electron |
| [19] | en.m.wikipedia.org/wiki/Energy_level |
| [20] | en.m.wikipedia.org/wiki/Helium |
| [21] | en.m.wikipedia.org/wiki/Iron-56 |
| [22] | en.m.wikipedia.org/wiki/Lorentz_force |
| [23] | hyperphysics.phy-astr.gsu.edu/hbase/magnetic/magfie.html#c1 |
| [24] | www.s-cool.co.uk/a-level/physics/nuclear-energy/revise-it/mass-defect |
| [25] | en.m.wikipedia.org/wiki/Mass-energy_equivalence |
| [26] | en.m.wikipedia.org/wiki/Neutrons |
| [27] | hyperphysics.phy-astr.gsu.edu/hbase/nucene/nucbin.html |
| [28] | en.m.wikipedia.org/wiki/Nuclear_binding_energy |
| [29] | hyperphysics.phy-astr.gsu.edu/hbase/fission.html |
| [30] | en.m.wikipedia.org/wiki/Nuclear_fission |
| [31] | www.atomicarchive.com/Fission/Fission1.shtml |
| [32] | hyperphysics.phy-astr.gsu.edu/hbase/nucene/fusion.html |
| [33] | en.m.wikipedia.org/wiki/Nuclear_fusion |
| [34] | en.m.wikipedia.org/wiki/Nuclear_shell_model |
| [35] | en.m.wikipedia.org/wiki/Orbital_speed |
| [36] | www2.ignatius.edu/faculty/decarlo/origin%20of%20the%20magnetic%20field.htm |
| [37] | physics.bu.edu/uduffy/sc546_notes10/mass_defect.html |
| [38] | en.m.wikipedia.org/wiki/Potential_energy |
| [39] | en.m.wikipedia.org/wiki/Proton |
| [40] | en.m.wikipedia.org/wiki/Proton_magnetic_moment |
| [41] | en.m.wikipedia.org/wiki/Radioactive_decay |
| [42] | en.m.wikipedia.org/wiki/Reduced_mass |
| [43] | en.m.wikipedia.org/wiki/Relativistic_quantum_mechanics |
| [44] | www.schoolphysics.co.uk/age16-19/Atomic%20physics/Electron%20physics/text/Electron_motion_in_electric_and_magnetic_fields/index.html |
| [45] | www.physicsoftheuniverse.com/topics_relativity_special.html-ag-physics.org/electron/ |
| [46] | staff.orecity.k12.or.us/les.sitton/Nuclear/313.htm |
| [47] | applet-magic.com/He4.htm |
| [48] | en.m.wikipedia.org/wiki/Unifeid_field_theory |
| [49] | en.m.wikipedia.org/wiki/Uranium-235 |


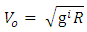
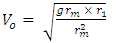
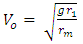
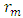 = Multiple of force producer radius to distance apart
= Multiple of force producer radius to distance apart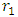 = force producer radius Escape velocity at any orbit,
= force producer radius Escape velocity at any orbit, 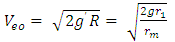
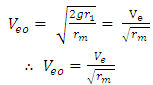
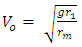 Which is
Which is  times less than Veo
times less than Veo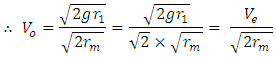 V0 – orbiting velocity round the earth
V0 – orbiting velocity round the earth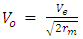
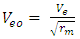
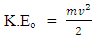
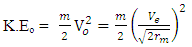 Where V = Vo and M- mass of orbiting body
Where V = Vo and M- mass of orbiting body 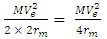
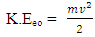 here V = Veo
here V = Veo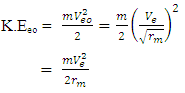

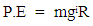
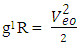
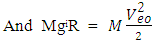
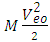 is the least energy it will use to escape that orbit.Therefore the P.E of any system is equal to the least energy needed to separate the system.For two magnets of like poles, the energy needed to separate them is equal to their P.E and the magnets will move at a velocity away from each other, which is equal to the escape velocity at that orbit.A body may be considered a system if no external force is acting on it, or if external force does not have effect on it. Total Energy in a system: the Binding EnergyConsider a system to be formed of N magnets having equal masses, and the distance between any two closest magnets is the same. The binding energy or P.E for all the bodies is the total energy used to hold them together.Total Binding energy
is the least energy it will use to escape that orbit.Therefore the P.E of any system is equal to the least energy needed to separate the system.For two magnets of like poles, the energy needed to separate them is equal to their P.E and the magnets will move at a velocity away from each other, which is equal to the escape velocity at that orbit.A body may be considered a system if no external force is acting on it, or if external force does not have effect on it. Total Energy in a system: the Binding EnergyConsider a system to be formed of N magnets having equal masses, and the distance between any two closest magnets is the same. The binding energy or P.E for all the bodies is the total energy used to hold them together.Total Binding energy 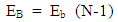

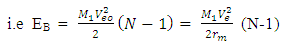
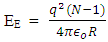
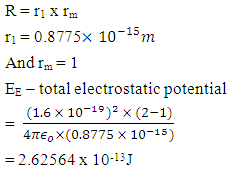
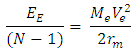 where Me – mass of electronThe escape velocity of electron at proton surface is
where Me – mass of electronThe escape velocity of electron at proton surface is 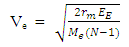
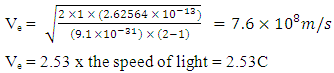 From Bohr’s theory on atomic model, the electron at the lowest energy level of a hydrogen atom has energy of 13.6eV (21.8 x 10-19J). This energy is the energy of the orbiting electron (E0)
From Bohr’s theory on atomic model, the electron at the lowest energy level of a hydrogen atom has energy of 13.6eV (21.8 x 10-19J). This energy is the energy of the orbiting electron (E0)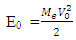
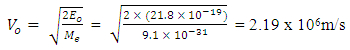 From
From 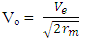
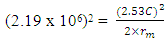
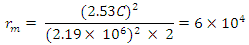
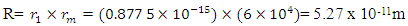 This is the centre radius between the orbiting electron and the proton in a hydrogen atom – or the radius of the hydrogen atom. Mathematical Models for Helium-4 StructureHelium-4 nucleus is extremely stable. To know the structure of this nucleus, some possible outcome of its structure will be subjected to two different tests:a. Atomic Radius Testb. Nuclear Fission (electromagnetic potential ) Energy TestP – ProtonN – Neutron Model i)
This is the centre radius between the orbiting electron and the proton in a hydrogen atom – or the radius of the hydrogen atom. Mathematical Models for Helium-4 StructureHelium-4 nucleus is extremely stable. To know the structure of this nucleus, some possible outcome of its structure will be subjected to two different tests:a. Atomic Radius Testb. Nuclear Fission (electromagnetic potential ) Energy TestP – ProtonN – Neutron Model i) 



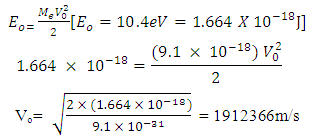 Atomic nucleus radius
Atomic nucleus radius 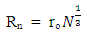
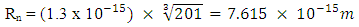
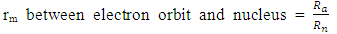
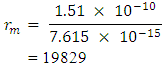 Test B: Nuclear Fission Energy TestIn nuclear fission, the absorption of a neutron by a heavy nuclide (e.g U-235) causes the nuclide to become unstable and break into light nuclides and additional neutrons. This positively charged light nuclide then repel, releasing electromagnetic potential energy.
Test B: Nuclear Fission Energy TestIn nuclear fission, the absorption of a neutron by a heavy nuclide (e.g U-235) causes the nuclide to become unstable and break into light nuclides and additional neutrons. This positively charged light nuclide then repel, releasing electromagnetic potential energy.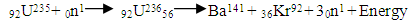 The fission of one atom of U-235 generates 202.5 MeV = 3.24 x10-11JThe Helium-4 model must meet these criterion or have values that are near rm = 19829 and Er = 3.24 x 10-11J(Where Er = energy released). Model ITest A: At rpp = 3.33r1 for the helium nucleus where rpp = p-p distance.Then from
The fission of one atom of U-235 generates 202.5 MeV = 3.24 x10-11JThe Helium-4 model must meet these criterion or have values that are near rm = 19829 and Er = 3.24 x 10-11J(Where Er = energy released). Model ITest A: At rpp = 3.33r1 for the helium nucleus where rpp = p-p distance.Then from 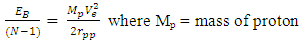 Helium-4 has atomic mass of 4.00260325415U = 6.64648 x10-27kgActual mass of 2 protons + 2 electrons + 2 neutrons = 6.697 x 10-27kg
Helium-4 has atomic mass of 4.00260325415U = 6.64648 x10-27kgActual mass of 2 protons + 2 electrons + 2 neutrons = 6.697 x 10-27kg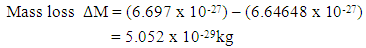 Total Binding Energy
Total Binding Energy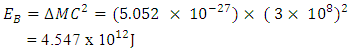
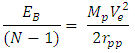 Number of nucleons in Helium-4 is 4
Number of nucleons in Helium-4 is 4 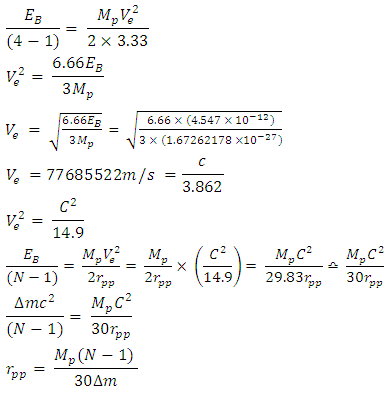
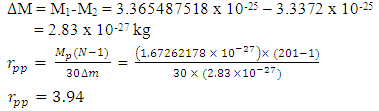 Radius between any two closest proton in a mercury-201nucleus is given by
Radius between any two closest proton in a mercury-201nucleus is given by 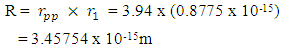 If an electron is brought to the mercury nucleus, and placed 3.45754 x 10-15m away from any proton, thereby increasing the total number of charge of the nucleus, then the electrostatic energy of the nucleus will be:
If an electron is brought to the mercury nucleus, and placed 3.45754 x 10-15m away from any proton, thereby increasing the total number of charge of the nucleus, then the electrostatic energy of the nucleus will be: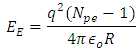 Where Npe – total number of protons + 1 electron added to the nucleus
Where Npe – total number of protons + 1 electron added to the nucleus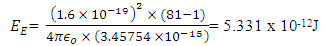 Energy between a proton and this electron:
Energy between a proton and this electron: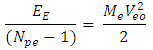 Velocity the electron will use to escape from this distance of 3.45754 x10-15m from the closest proton:
Velocity the electron will use to escape from this distance of 3.45754 x10-15m from the closest proton: 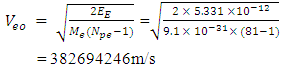 Since this velocity is the velocity at the nucleus, it can be regarded as the escape velocity Ve when compared to that used by the electron to orbit the nucleus 1.51 x 10-10m away.
Since this velocity is the velocity at the nucleus, it can be regarded as the escape velocity Ve when compared to that used by the electron to orbit the nucleus 1.51 x 10-10m away. 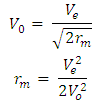 Recall that the velocity of the orbiting electron in Mercury–201 atom is 1912366m/s
Recall that the velocity of the orbiting electron in Mercury–201 atom is 1912366m/s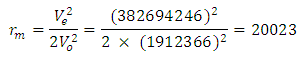
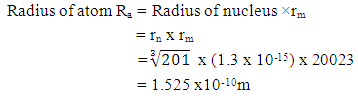 This compares well with the known 1.51 x 10-10m (empirical radius)Test B: Nuclear fission (Electromagnetic potential) Energy TestEnergy released = Electromagnetic potential energy in nucleusThe nucleus in question here is Uranium–235, whose isotope mass number is 235.0439299U = 3.903 x 10-25kg, atomic number = 92; number of neutron = 143Actual mass of 92 protons + 92 electrons + 143 neutronsM1 = 3.9348 x 10-25kg Mass loss
This compares well with the known 1.51 x 10-10m (empirical radius)Test B: Nuclear fission (Electromagnetic potential) Energy TestEnergy released = Electromagnetic potential energy in nucleusThe nucleus in question here is Uranium–235, whose isotope mass number is 235.0439299U = 3.903 x 10-25kg, atomic number = 92; number of neutron = 143Actual mass of 92 protons + 92 electrons + 143 neutronsM1 = 3.9348 x 10-25kg Mass loss 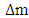 = M1-M2 = (3.9348 x 10-25) – (3.903 x10-25)= 3.179535 x 10-27Kg
= M1-M2 = (3.9348 x 10-25) – (3.903 x10-25)= 3.179535 x 10-27Kg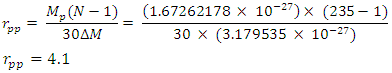 Radius between any two closest protons in the nucleus
Radius between any two closest protons in the nucleus 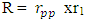
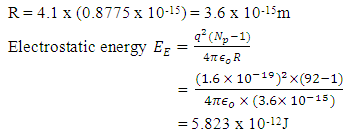 Magnetic potential Energy
Magnetic potential Energy 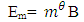
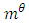 = magnetic moment of a proton, which is equal to 1.410606743 x 10-26J/T
= magnetic moment of a proton, which is equal to 1.410606743 x 10-26J/T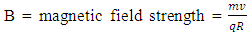
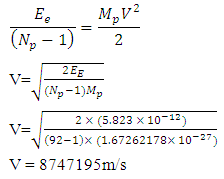 Magnetic fields are produced by electric currents. The protons in a nucleus has magnetic properties because of the charge they carry. The electrostatic energy between the protons will cause them to move away from each other at a velocity (V which is equal to 8747195m/s for the uranium-235); thereby generating magnetic energy.The magnetic field strength
Magnetic fields are produced by electric currents. The protons in a nucleus has magnetic properties because of the charge they carry. The electrostatic energy between the protons will cause them to move away from each other at a velocity (V which is equal to 8747195m/s for the uranium-235); thereby generating magnetic energy.The magnetic field strength 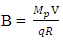
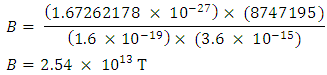 Since each proton repels the other 91 protons in the nucleus, the magnetic potential energy for the nucleus is given by
Since each proton repels the other 91 protons in the nucleus, the magnetic potential energy for the nucleus is given by 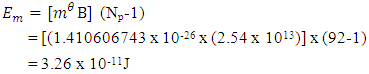 This compares well with the 3.24 x 10-11J energy released during fission of Uranium-235ResultsTable of Result for all the Models:
This compares well with the 3.24 x 10-11J energy released during fission of Uranium-235ResultsTable of Result for all the Models: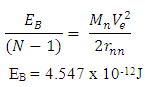
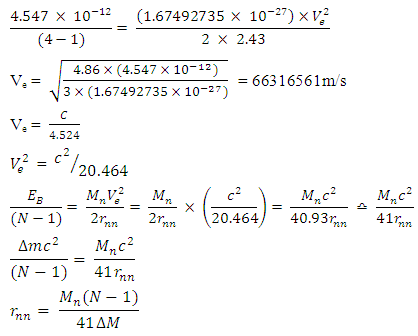
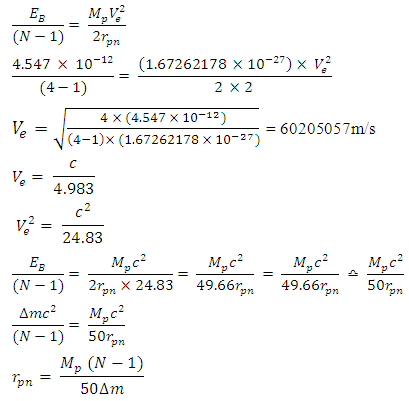
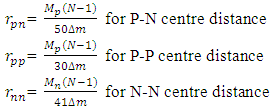 Note the distance R = r1 x rmwhere rm = rpp or rpn or rnnFrom the above table, it can be seen that P-N, P-P and N-N are closest at Iron–56. This means Iron-56 from the table above has the greatest bond between any two nucleons in the nucleus.
Note the distance R = r1 x rmwhere rm = rpp or rpn or rnnFrom the above table, it can be seen that P-N, P-P and N-N are closest at Iron–56. This means Iron-56 from the table above has the greatest bond between any two nucleons in the nucleus.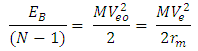 Where m = mass of the smaller nucleon and
Where m = mass of the smaller nucleon and 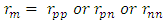 From Tab 2.3 one can look for the binding energy for each nucleus and find the relationship between them. It can be seen from the table that
From Tab 2.3 one can look for the binding energy for each nucleus and find the relationship between them. It can be seen from the table that 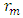 is increasing. A good relationship between the binding energy between any two nucleons in a nucleus and the distance apart will be used to formulate a new equation.Mathematical Models:i) Magnesium–24 has binding energy between any two closest proton and neutron
is increasing. A good relationship between the binding energy between any two nucleons in a nucleus and the distance apart will be used to formulate a new equation.Mathematical Models:i) Magnesium–24 has binding energy between any two closest proton and neutron 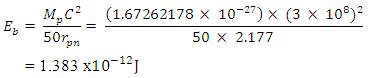 ii) Molybdenum–96 has binding energy between any two closest proton and neutron
ii) Molybdenum–96 has binding energy between any two closest proton and neutron 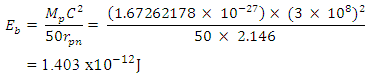 iii) Uranium–238 has binding energy between any two closest proton and neutron
iii) Uranium–238 has binding energy between any two closest proton and neutron 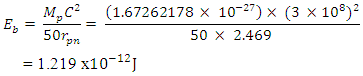
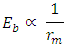
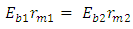 Mathematical Model:What is the centre-centre multiple distance for Iron-56 if the binding energy between any proton and neutron in an Iron-56 nucleus is 1.432 x 10-12J. (Take binding energy of Magnesium-24 and centre–to–centre multiple of its closest proton and neutron to be 1.383 x 10-12J and 2.177 respectively.)
Mathematical Model:What is the centre-centre multiple distance for Iron-56 if the binding energy between any proton and neutron in an Iron-56 nucleus is 1.432 x 10-12J. (Take binding energy of Magnesium-24 and centre–to–centre multiple of its closest proton and neutron to be 1.383 x 10-12J and 2.177 respectively.)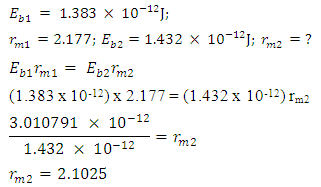 This can be compared with 2.102 which is in the table. Mathematical Model:An unknown element has binding energy between two of its closest nucleons as
This can be compared with 2.102 which is in the table. Mathematical Model:An unknown element has binding energy between two of its closest nucleons as 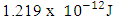 , and the centre distance between the two nucleons is 2.469. What will be the binding energy between any two closest nucleons of Molybdenum-96, whose centre–to–centre distance multiple is 2.146
, and the centre distance between the two nucleons is 2.469. What will be the binding energy between any two closest nucleons of Molybdenum-96, whose centre–to–centre distance multiple is 2.146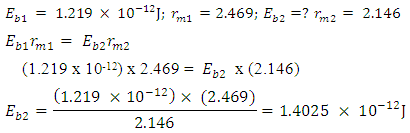 This compares well with the 1.403 x
This compares well with the 1.403 x 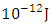 of the Molybdenum–96 Conclusion:From the above, it can be concluded that the binding energy between any two nucleons is inversely proportional to their distance apart
of the Molybdenum–96 Conclusion:From the above, it can be concluded that the binding energy between any two nucleons is inversely proportional to their distance apart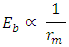 Also the total binding energy in any nucleus is given byEB = Eb (N-1)Energy = force x Distance = FRHypothesis on Nuclear Forces states that The force of attraction between any two nucleons held by nuclear forces, separated a distance R is proportional to the product of their masses and inversely proportional to the square root of their distance apart.
Also the total binding energy in any nucleus is given byEB = Eb (N-1)Energy = force x Distance = FRHypothesis on Nuclear Forces states that The force of attraction between any two nucleons held by nuclear forces, separated a distance R is proportional to the product of their masses and inversely proportional to the square root of their distance apart. 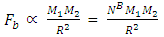
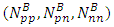 Energy is needed to bring a mass from infinity to the point in question, R.
Energy is needed to bring a mass from infinity to the point in question, R.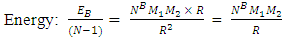
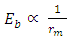 This present itself in a new form as:
This present itself in a new form as: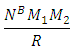 where
where 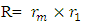 Self Energy of Every Nucleon
Self Energy of Every Nucleon 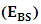 This is the self potential of every nucleon, and it is given by
This is the self potential of every nucleon, and it is given by 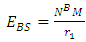
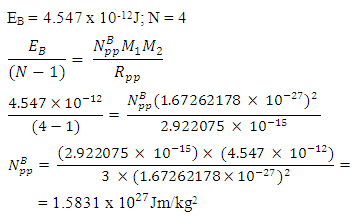
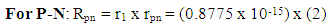
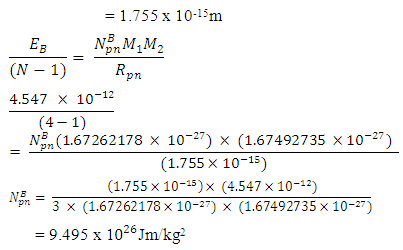
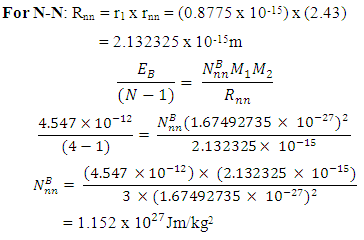 The nuclear force hypothesis when N> 2 for P-P, P-N and N-N
The nuclear force hypothesis when N> 2 for P-P, P-N and N-N 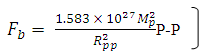
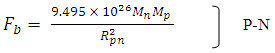
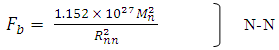
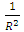 becomes
becomes 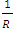 The total binding energy EB of any nucleus is given by:
The total binding energy EB of any nucleus is given by: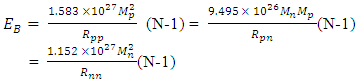 Mathematical Model: What is the centre-to-centre distance between any two closest neutrons in Tungsten–184 nucleus? Binding energy of Tungsten nucleus is 2.3631 x 10-10J. From the hypothesis of nuclear forces, when N>2,
Mathematical Model: What is the centre-to-centre distance between any two closest neutrons in Tungsten–184 nucleus? Binding energy of Tungsten nucleus is 2.3631 x 10-10J. From the hypothesis of nuclear forces, when N>2, 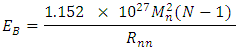

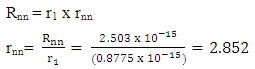 This compares well with the 2.847 that is in Tab 2.3.
This compares well with the 2.847 that is in Tab 2.3.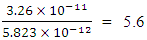 times smaller than the magnetic potential energy in the nucleus.Neither is the energy released an addition of the magnetic and electrostatic potential energy.In fact, the above three examples shows that the force of attraction on a revolving body is not a sum of the electrical and magnetic force or magnetic and gravitational force. Mathematical Models to Prove that the Magnetic Potential Energy is Dominant than the Electrical Energy at the NucleusTo prove why the magnetic field is dominant at the nucleus level, a simple nucleus (Hydrogen) shall be tested mathematically:Hydrogen: N = 1, proton radius = r1= 0.8775 x 10-15m, radius of atom Ra = 5.27 x 10-11m If a proton is placed near the proton (nucleus) of a hydrogen atom, at 2r1 away, then the electrostatic force of attraction will be
times smaller than the magnetic potential energy in the nucleus.Neither is the energy released an addition of the magnetic and electrostatic potential energy.In fact, the above three examples shows that the force of attraction on a revolving body is not a sum of the electrical and magnetic force or magnetic and gravitational force. Mathematical Models to Prove that the Magnetic Potential Energy is Dominant than the Electrical Energy at the NucleusTo prove why the magnetic field is dominant at the nucleus level, a simple nucleus (Hydrogen) shall be tested mathematically:Hydrogen: N = 1, proton radius = r1= 0.8775 x 10-15m, radius of atom Ra = 5.27 x 10-11m If a proton is placed near the proton (nucleus) of a hydrogen atom, at 2r1 away, then the electrostatic force of attraction will be 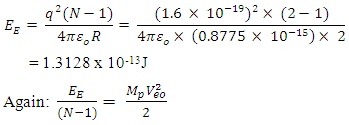 The escape velocity of this proton is
The escape velocity of this proton is 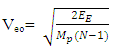
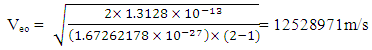 Also from
Also from 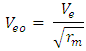 Note: From equation (2.2)
Note: From equation (2.2) 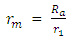 At 2r1, Veo = 12528971m/s is taken as the escape velocity Ve, so that
At 2r1, Veo = 12528971m/s is taken as the escape velocity Ve, so that 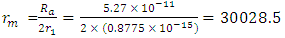
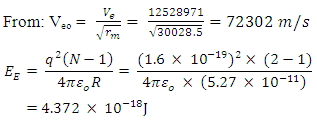 The Magnetic Potential Energy at both points
The Magnetic Potential Energy at both points 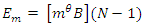 Where
Where 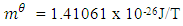
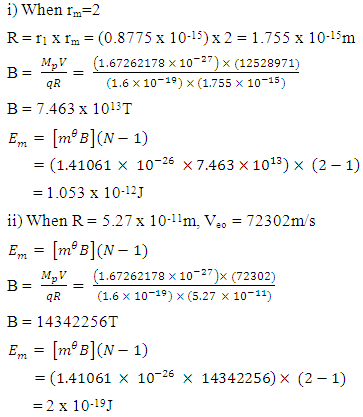 Results:EE at 1.755 x 10-15m = 1.3128 x 10-13 Jand at 5.27 x 10-11m = 4.372 x 10-18JEm at 1.755 x 10-15 = 1.053 x 10-12Jand at 5.27 x 10-11m = 2 x 10-19JConclusion: It is seen that the magnetic potential energy is greater than the electrostatic potential energy at the nucleus level, but at the atomic (radius) level the electrical energy is greater than the magnetic potential energy. Hypothesis of Superior Forces/Energystates: The potential or kinetic energy possessed by a body under a non–contact (electric, magnetic, gravitational or nuclear) field is a measure of the superior force field. Explanation: Beyond the atomic level magnetic force brings about bending effect, whereas gravitational and electrostatic force causes continuous movement. Net Energy in the NucleusTo know the net forces acting on any nucleus, it is assumed that the hypothesis of superior forces does not hold.Next, the forces (or total force) acting on the nucleus is divided into two—attracting and repulsive forces.The net force on the nucleus system is therefore
Results:EE at 1.755 x 10-15m = 1.3128 x 10-13 Jand at 5.27 x 10-11m = 4.372 x 10-18JEm at 1.755 x 10-15 = 1.053 x 10-12Jand at 5.27 x 10-11m = 2 x 10-19JConclusion: It is seen that the magnetic potential energy is greater than the electrostatic potential energy at the nucleus level, but at the atomic (radius) level the electrical energy is greater than the magnetic potential energy. Hypothesis of Superior Forces/Energystates: The potential or kinetic energy possessed by a body under a non–contact (electric, magnetic, gravitational or nuclear) field is a measure of the superior force field. Explanation: Beyond the atomic level magnetic force brings about bending effect, whereas gravitational and electrostatic force causes continuous movement. Net Energy in the NucleusTo know the net forces acting on any nucleus, it is assumed that the hypothesis of superior forces does not hold.Next, the forces (or total force) acting on the nucleus is divided into two—attracting and repulsive forces.The net force on the nucleus system is therefore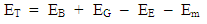
 This is negligible when compared with the electrostatic potential energy, which is:
This is negligible when compared with the electrostatic potential energy, which is: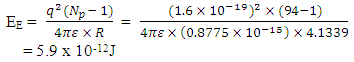 The new equation for the net energy then becomes:
The new equation for the net energy then becomes: 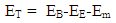
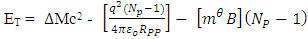
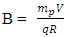 and Np = number of protons in nucleus
and Np = number of protons in nucleus 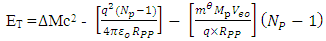
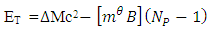
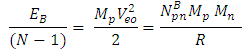 From Lorentz transformation, new length due to V is given by the equation:
From Lorentz transformation, new length due to V is given by the equation: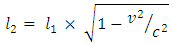 For the proton and neutron which has escape velocity compared to C, there will be a change in their radius, so that the new radius will be:
For the proton and neutron which has escape velocity compared to C, there will be a change in their radius, so that the new radius will be: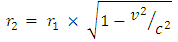 Where V= escape velocity of the nucleon r1 = original radius of the nucleon (proton or neutron)From
Where V= escape velocity of the nucleon r1 = original radius of the nucleon (proton or neutron)From 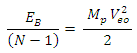
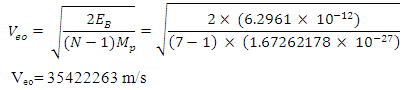 The new radius of the proton will be
The new radius of the proton will be 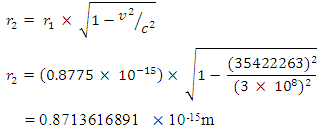
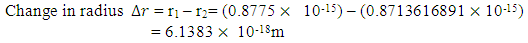 But the total self energy of every nuclear in the nucleus is constant provided no external energy disturb or is acting on the system. The self energy for one nucleon (proton):
But the total self energy of every nuclear in the nucleus is constant provided no external energy disturb or is acting on the system. The self energy for one nucleon (proton): 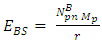 Before change in radius = r1After change in radius = r2Before change in radius
Before change in radius = r1After change in radius = r2Before change in radius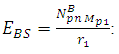 From equation (3.5) when N>2,
From equation (3.5) when N>2, 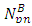 = 9.495 x 1026Jm/Kg2
= 9.495 x 1026Jm/Kg2 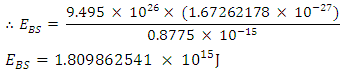 From Lorentz transformation there will be change in radius of the nucleus. This change in radius will lead to a change in mass for the self energy to remain constant since no external force is acting on the system. So that
From Lorentz transformation there will be change in radius of the nucleus. This change in radius will lead to a change in mass for the self energy to remain constant since no external force is acting on the system. So that 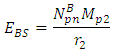
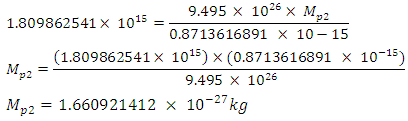 If (Mp1- Mp2) is the mass loss between the proton and neutron, total mass loss is given by
If (Mp1- Mp2) is the mass loss between the proton and neutron, total mass loss is given by 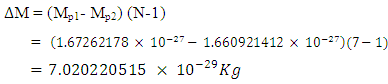
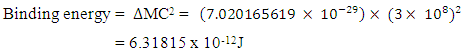 This is in agreement with the accepted value 6.2960508 x 10-12JIt is represented thus:
This is in agreement with the accepted value 6.2960508 x 10-12JIt is represented thus: R = uncharged, but r1 and r2 changes
R = uncharged, but r1 and r2 changes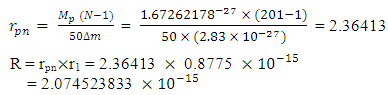 Mercury-201 has its electron lowest energy level at 1.51 x 10-10m which is 19829 x the radius of the nucleus
Mercury-201 has its electron lowest energy level at 1.51 x 10-10m which is 19829 x the radius of the nucleus  If a neutron is brought to the Mercury nucleus, and placed 2.074523833
If a neutron is brought to the Mercury nucleus, and placed 2.074523833 m away from any proton, thereby increasing the mass of the nucleus, then the nuclear energy of the nucleus will be:
m away from any proton, thereby increasing the mass of the nucleus, then the nuclear energy of the nucleus will be: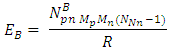 Where NNn--is the sum of the nucleons in the nucleus and the neutron added to it
Where NNn--is the sum of the nucleons in the nucleus and the neutron added to it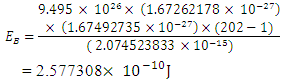 Energy between a proton and this neutron added to the nucleus:
Energy between a proton and this neutron added to the nucleus: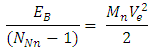 Ve is the velocity the added neutron will use to escape from the nucleus to
Ve is the velocity the added neutron will use to escape from the nucleus to 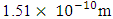 away from the centre of the nucleus, which is the region with the lowest energy level of the electron.
away from the centre of the nucleus, which is the region with the lowest energy level of the electron.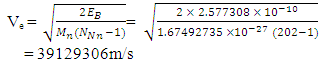 But
But 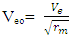 Recall that the radius multiple rm, between Mercury-201 nucleus and its empirical atomic radius is 19829Therefore,
Recall that the radius multiple rm, between Mercury-201 nucleus and its empirical atomic radius is 19829Therefore, 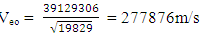 New radius of the neutron at a distance of
New radius of the neutron at a distance of 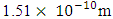 will be:
will be: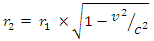
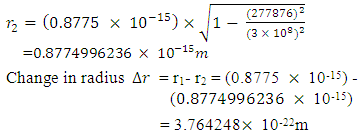 To know the mass loss, we first find the self potential energy:
To know the mass loss, we first find the self potential energy: 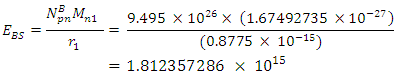 Also
Also 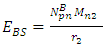
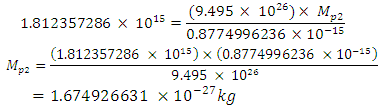
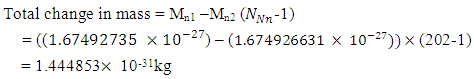
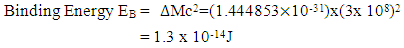 Solving for
Solving for  and
and 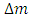 when the added neutron is
when the added neutron is 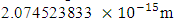 away from a proton in the nucleus:Recall that the escape velocity at this point is 39129306m/s.From Lorentz Transformation,
away from a proton in the nucleus:Recall that the escape velocity at this point is 39129306m/s.From Lorentz Transformation, 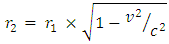
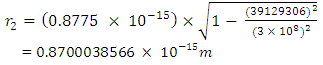
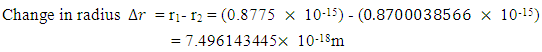 To know the mass loss, we first find the self potential energy:
To know the mass loss, we first find the self potential energy: 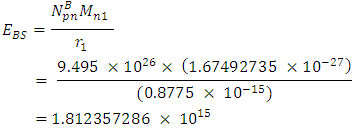 Also
Also 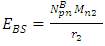
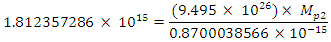
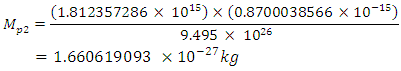
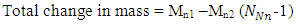
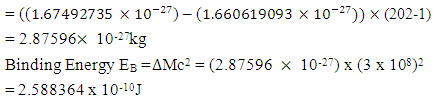 This binding energy is in agreement with the
This binding energy is in agreement with the 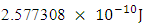 earlier gottenResults
earlier gottenResults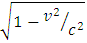 will bring about a considerable change in mass and radius Therefore M1> M2 and r1> r2For two or more nucleons to be held by nuclear energy, they must be brought under high velocity that is, they will have enough velocity to overcome each other’s repulsion (when there is more than one proton) - There must be a considerable change in mass- There must be a considerable change in radius of the nucleons- The least velocity at which they will be separated after they are joined together, must be comparable to the speed of light From the table of result above, it can be seen that the loss in mass, change in velocity and radius of the neutron when it is
will bring about a considerable change in mass and radius Therefore M1> M2 and r1> r2For two or more nucleons to be held by nuclear energy, they must be brought under high velocity that is, they will have enough velocity to overcome each other’s repulsion (when there is more than one proton) - There must be a considerable change in mass- There must be a considerable change in radius of the nucleons- The least velocity at which they will be separated after they are joined together, must be comparable to the speed of light From the table of result above, it can be seen that the loss in mass, change in velocity and radius of the neutron when it is 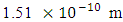 away is very small when compared to when it is
away is very small when compared to when it is 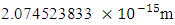 from the nearest proton.
from the nearest proton.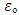 = 8.854 X 10-12F/mGravitational Constant = 6.7 X 10-11Nm2/kg2
= 8.854 X 10-12F/mGravitational Constant = 6.7 X 10-11Nm2/kg2 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML