Hesham Mansour , Ahmed Gamal
Physics Department, Faculty of Science, Cairo University, Egypt
Correspondence to: Hesham Mansour , Physics Department, Faculty of Science, Cairo University, Egypt.
| Email: |  |
Copyright © 2016 Scientific & Academic Publishing. All Rights Reserved.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/

Abstract
A complete solution of the Schrodinger equation is given for the heavy quark-antiquark bound states. A confining harmonic plus an harmonic potential are used with a 1/r singular potential. We use the method of the Eigen value problem by asymptotic iteration. The results are good in comparison with the experimental data.
Keywords:
Schrodingers equation, Heavy quarks, Bound states
Cite this paper: Hesham Mansour , Ahmed Gamal , Heavy Quark Bound States, Journal of Nuclear and Particle Physics, Vol. 6 No. 1, 2016, pp. 6-9. doi: 10.5923/j.jnpp.20160601.02.
1. Introduction
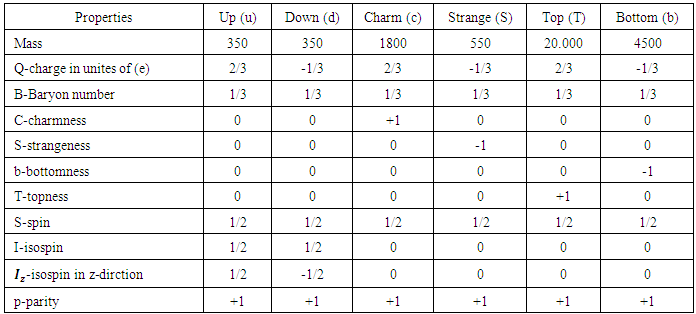
A quark is an elementary particle and a fundamental constituent of matter [1-4]. Quarks combine to form composite particles called hadrons [2, 3]. Quarks are never directly observed or found in isolation; they can be found only within hadrons, such as baryons and mesons [2, 3]. Quarks have various intrinsic properties, including electric charge, mass, color charge and spin [2, 3]. There are six types of quarks, known as flavors: up, down, strange, charm, top, and bottom. Up and down quarks, have the lowest masses of all quarks [1-3].The heavier quarks rapidly change into up and down quarks through a process of particle decay: the transformation from a higher mass state to a lower mass state. Because of this, up and down quarks are generally stable and the most common in the universe, whereas strange, charm, bottom, and top quarks can only be produced in high energy collisions (such as those involving cosmic rays and in particle accelerators) [1-3]. For every quark flavor there is a corresponding type of antiparticle, known as an antiquark, that differs from the quark only in that some of its properties have equal magnitude but opposite sign [1-3, 5].They are simple structure less, particles with fractional electric charge; point likeand spin-1/2 and they have positive parity, see table 1. Anti quarks have negative parity. The strong interaction between the quarks originates from the gluon field. Its field quanta are the gluons [1-3, 5]. Quarks do not interact with each other directly; they do so through intermediate agents called gluons which are massless, spin-1 particles.Table 1. Characteristics of the quarks
 |
| |
|
2. Asymptotic Freedom
According to QCD (Quantum chromo dynamics) [1, 3, 5], the force between quarks is actually rather weak as long as the quarks are close together, closer than 1fermi. One Fermi is approximately the size of a proton) [6]. This weakness of the force between nearby quarks is called "asymptotic freedom". Asymptotic freedom is a property of the QCD vacuum, which describes how it responds to an "extra quark" [6]. Because of the weakness of the force at short distances and the fact that the b and c quarks are heavy anon relativistic approach is commonly used. Many potentials are adopted for such systems.
3. Theory and Calculations
In the present work, we will use non-relativistic Schrödinger equation because the quarks b and c are heavy. The Hamiltonian equation for a bound quark and anti quark in general is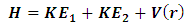 | (1) |
the potentials used are
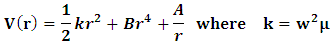 where the harmonic and an harmonic terms are responsible for the confinement of the bound particles and the 1/r potential for the interaction of the charges. The Hamiltonian equation becomes
where the harmonic and an harmonic terms are responsible for the confinement of the bound particles and the 1/r potential for the interaction of the charges. The Hamiltonian equation becomes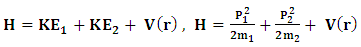 | (2) |
and the Schrodinger equation is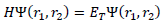 | (3) |
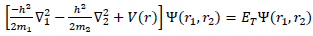 | (4) |
the solution of this equation is presented in many bookse.g. see Ref. [7]. The solution is a product of the center of mass and relative motions. Here we are interested in the solution of the radial part R (r) of the relative motion [8].The redused mass for the two particles of masses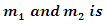
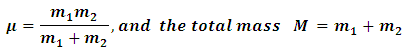 The radial Schrödinger equation is [7]
The radial Schrödinger equation is [7] 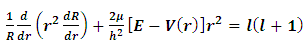 | (5) |
let 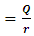 , hence the equation becomes
, hence the equation becomes 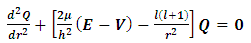 | (6) |
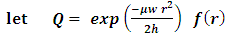 | (7) |
we get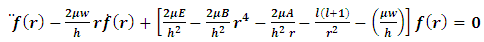 | (8) |
Where the dot means a derivative with respect to r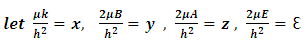 | (9) |
and rearranging equation (8). We get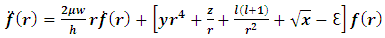 | (10) |
we will use and follow the asymptotic iteration method for eigenvalue problems [8].Using the same notations, we define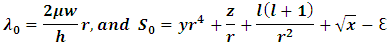 The choice of r can be critical to the speed of the convergence to the eigenvalues, as well as for the stability of the process. Although, we do not have at the moment a specific method to determine the best initial value of r, so we may suggest the following approach:We note that the ground state energy of this potential can be obtained by setting
The choice of r can be critical to the speed of the convergence to the eigenvalues, as well as for the stability of the process. Although, we do not have at the moment a specific method to determine the best initial value of r, so we may suggest the following approach:We note that the ground state energy of this potential can be obtained by setting  we may therefore start our iteration with
we may therefore start our iteration with  obtained from
obtained from 
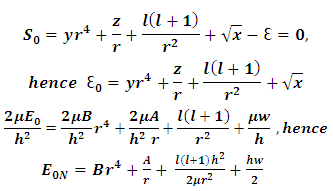 | (11) |
where 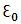 is a function of (y, r, z, l and x) , and
is a function of (y, r, z, l and x) , and 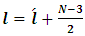 where
where 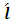 is the angular momentum quantum number , and N is dimensionless,
is the angular momentum quantum number , and N is dimensionless, 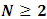 .for
.for 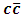 system [2,3]: we will consider the different S-state levels using the available experimental total masses
system [2,3]: we will consider the different S-state levels using the available experimental total masses 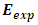 [9], we know that
[9], we know that 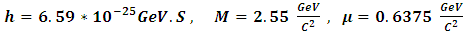 the binding energy is equal to the experimental energy minus M according to this equation
the binding energy is equal to the experimental energy minus M according to this equation 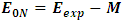 . Hence, in order to get the binding energy of the levels one must find the coefficients (A, B, r, and w) in equation 11. To do that we will use the experimental data given for the lowest three states of the bound system [9].First, we try to find (r)case (1)
. Hence, in order to get the binding energy of the levels one must find the coefficients (A, B, r, and w) in equation 11. To do that we will use the experimental data given for the lowest three states of the bound system [9].First, we try to find (r)case (1)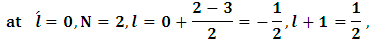
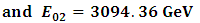 substituting in equation (11), we get
substituting in equation (11), we get 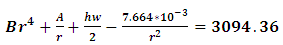 | (12) |
case (2)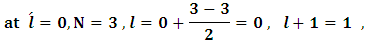
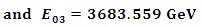 substituting in equation (11), we get
substituting in equation (11), we get 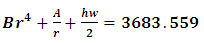 | (13) |
subtracted equation (12) from (13), we get 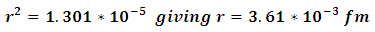 | (14) |
Substituting in equation (13), we get 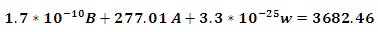 | (15) |
similarly, for the cases of the levels N=4 and 5, we get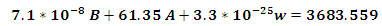 | (16) |
and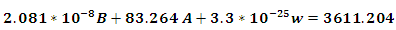 | (17) |
we will subtract equation (15) from (16), to get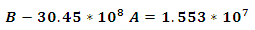 | (18) |
we will subtract equation (16) from (17)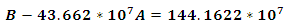 | (19) |
we will subtract equation (18) from (19).Finally, the coefficients of the potential using the first experimental lower levels of the bound states [10] by solving equations 15, 16 and 17 are obtained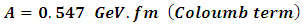 | (20) |
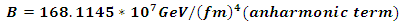 | (21) |
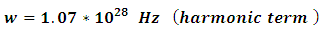 | (22) |
Having obtained the parameters of the suggested potential, we will proceed to calculate the energy levels of the bound system.Now, we will find the value 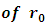 , to start our iteration and find the eigenvalues of the bound states and compare them with the experimental data. Substituting the coefficients in equation (11)in case (1)
, to start our iteration and find the eigenvalues of the bound states and compare them with the experimental data. Substituting the coefficients in equation (11)in case (1)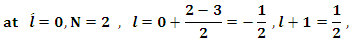
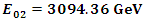 we get
we get 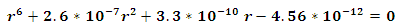 the solution of this equation is
the solution of this equation is 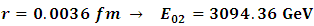 in case (2)
in case (2)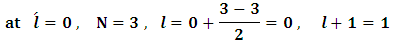 we get
we get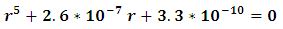 the solution of this equation is
the solution of this equation is 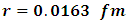 substituting the value of
substituting the value of 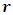 in the equation (11) and obtain the value of the energy
in the equation (11) and obtain the value of the energy 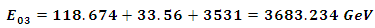 | (23) |
in case (3)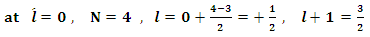 we get
we get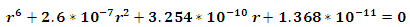 the solution of this equation is
the solution of this equation is 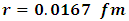 substituting the value of
substituting the value of 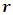 in equation (11) and obtain the value of the energy
in equation (11) and obtain the value of the energy 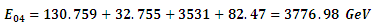 | (24) |
in case (4)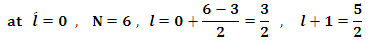 we get
we get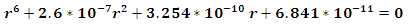 the solution of this equation is
the solution of this equation is 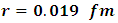 substituting the value of
substituting the value of 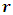 in equation (11) and obtain the value of the energy
in equation (11) and obtain the value of the energy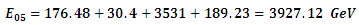 | (25) |
in case (5)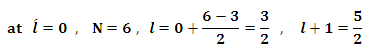 we get
we get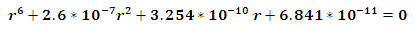 the solution of this equation is
the solution of this equation is 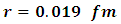 substituting the value of
substituting the value of 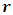 in equation (11) and obtain the value of the energy
in equation (11) and obtain the value of the energy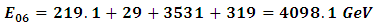 | (26) |
in case (6)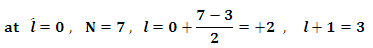 we get
we get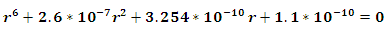 the solution of this equation is
the solution of this equation is 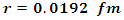 substituting the value of
substituting the value of 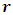 in equation (11) and obtain the value of the energy
in equation (11) and obtain the value of the energy 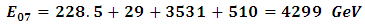 | (27) |
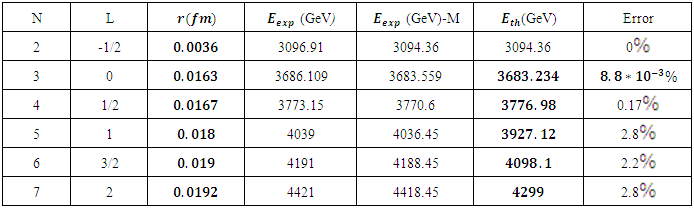
In table (2) a comparison between the experimental data and theoretical results are presented.Similarly in the 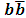 system [2, 3]
system [2, 3]Table 2
 |
| |
|
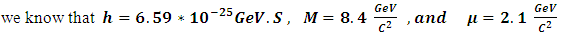 the coefficients of the potentials are as follows
the coefficients of the potentials are as follows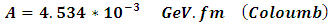 | (28) |
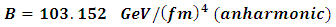 | (29) |
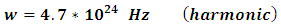 | (30) |
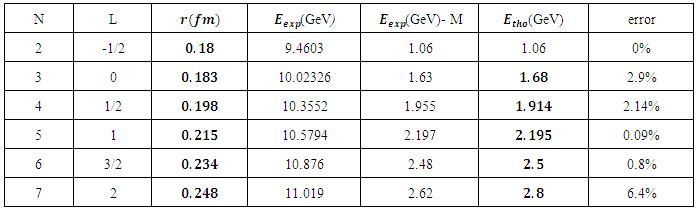
In table (3) a comparison between the experimental data and theoretical results are shown.Table 3
 |
| |
|
4. Conclusions
In the present work we used the result of the asymptotic iteration method for eigenvalue problems [8] to make fitting of the parameters of the potential with the experimental data of the bound 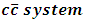 and
and 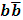 system. We chose the harmonic, an harmonic plus, Coulomb, potentials to solve the non-relativistic Schrodinger equation. The results give good agreement with the experimental data [9] with maximum error 2.8%
system. We chose the harmonic, an harmonic plus, Coulomb, potentials to solve the non-relativistic Schrodinger equation. The results give good agreement with the experimental data [9] with maximum error 2.8% 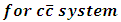 and 6.4%
and 6.4% 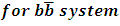 .
.
References
| [1] | D. Griffiths, 1987, Introduction to Elementary Particles. |
| [2] | Donald H. Perkins, 2000, Introduction to High Energy Physics. |
| [3] | B. R. Martin, Graham G. Shaw, 2nd Edition, 1997, Particle Physics. |
| [4] | F. Halzem, A. Martin, 1984, Quarks and Leptons: An Introductory Course in Modern Particle Physics, see also Emmanuel Olaiya, lectures: Introduction to elementary Particle Physics. |
| [5] | JOHAN RATHSMAN, 1996, Quark and Lepton Interactions. |
| [6] | Dr. Rasool Javahery, 2001, article the free quarks. |
| [7] | Nouredine Zettili, 2009, Second Edition, Quantum Mechanics Concepts and Applications. |
| [8] | Hakan cifftci, Richard L. hall and Nasser saad, J. phys. A Math. Gen.36, 2003, 11807, see also T. Barakat, J. Phys. A: Math. Gen. 39 (2006) 823. |
| [9] | Chin. Phys. C, 38, 090001 - Particle Data Group. |


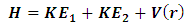

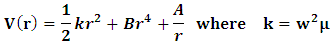 where the harmonic and an harmonic terms are responsible for the confinement of the bound particles and the 1/r potential for the interaction of the charges. The Hamiltonian equation becomes
where the harmonic and an harmonic terms are responsible for the confinement of the bound particles and the 1/r potential for the interaction of the charges. The Hamiltonian equation becomes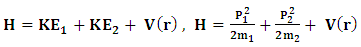
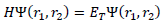
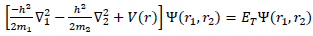
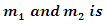
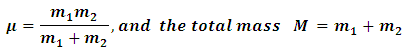 The radial Schrödinger equation is [7]
The radial Schrödinger equation is [7] 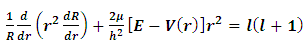
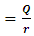 , hence the equation becomes
, hence the equation becomes 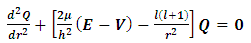
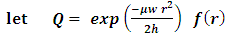
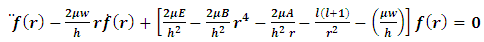
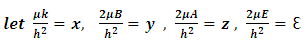
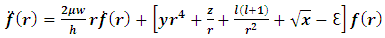
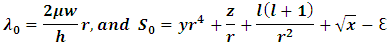 The choice of r can be critical to the speed of the convergence to the eigenvalues, as well as for the stability of the process. Although, we do not have at the moment a specific method to determine the best initial value of r, so we may suggest the following approach:We note that the ground state energy of this potential can be obtained by setting
The choice of r can be critical to the speed of the convergence to the eigenvalues, as well as for the stability of the process. Although, we do not have at the moment a specific method to determine the best initial value of r, so we may suggest the following approach:We note that the ground state energy of this potential can be obtained by setting 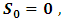 we may therefore start our iteration with
we may therefore start our iteration with 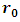 obtained from
obtained from 
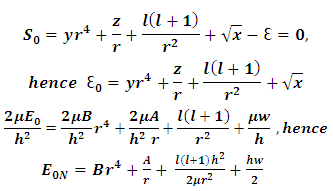
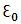 is a function of (y, r, z, l and x) , and
is a function of (y, r, z, l and x) , and 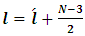 where
where 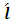 is the angular momentum quantum number , and N is dimensionless,
is the angular momentum quantum number , and N is dimensionless, 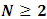 .for
.for 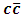 system [2,3]: we will consider the different S-state levels using the available experimental total masses
system [2,3]: we will consider the different S-state levels using the available experimental total masses 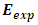 [9], we know that
[9], we know that 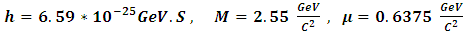 the binding energy is equal to the experimental energy minus M according to this equation
the binding energy is equal to the experimental energy minus M according to this equation 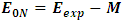 . Hence, in order to get the binding energy of the levels one must find the coefficients (A, B, r, and w) in equation 11. To do that we will use the experimental data given for the lowest three states of the bound system [9].First, we try to find (r)case (1)
. Hence, in order to get the binding energy of the levels one must find the coefficients (A, B, r, and w) in equation 11. To do that we will use the experimental data given for the lowest three states of the bound system [9].First, we try to find (r)case (1)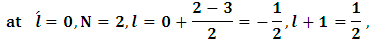
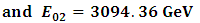 substituting in equation (11), we get
substituting in equation (11), we get 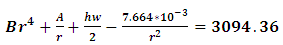
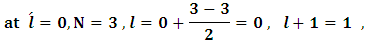
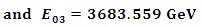 substituting in equation (11), we get
substituting in equation (11), we get 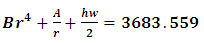
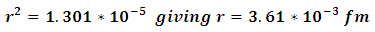
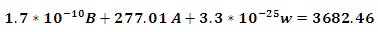
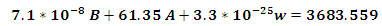
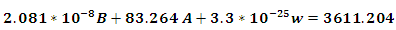
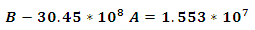
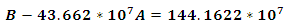
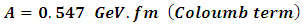
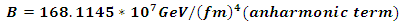
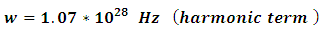
 , to start our iteration and find the eigenvalues of the bound states and compare them with the experimental data. Substituting the coefficients in equation (11)in case (1)
, to start our iteration and find the eigenvalues of the bound states and compare them with the experimental data. Substituting the coefficients in equation (11)in case (1)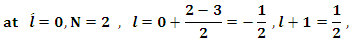
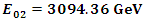 we get
we get 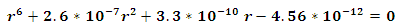 the solution of this equation is
the solution of this equation is 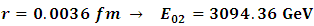 in case (2)
in case (2)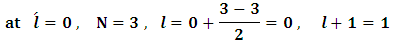 we get
we get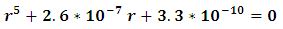 the solution of this equation is
the solution of this equation is 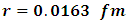 substituting the value of
substituting the value of 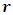 in the equation (11) and obtain the value of the energy
in the equation (11) and obtain the value of the energy 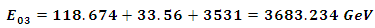
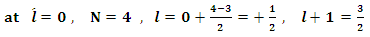 we get
we get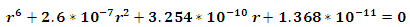 the solution of this equation is
the solution of this equation is 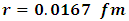 substituting the value of
substituting the value of  in equation (11) and obtain the value of the energy
in equation (11) and obtain the value of the energy 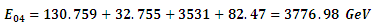
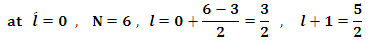 we get
we get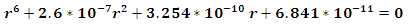 the solution of this equation is
the solution of this equation is 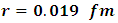 substituting the value of
substituting the value of 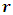 in equation (11) and obtain the value of the energy
in equation (11) and obtain the value of the energy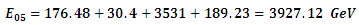
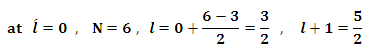 we get
we get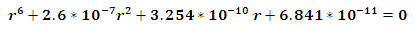 the solution of this equation is
the solution of this equation is 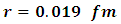 substituting the value of
substituting the value of 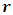 in equation (11) and obtain the value of the energy
in equation (11) and obtain the value of the energy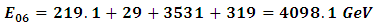
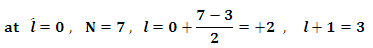 we get
we get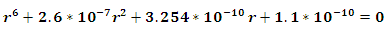 the solution of this equation is
the solution of this equation is 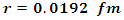 substituting the value of
substituting the value of 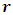 in equation (11) and obtain the value of the energy
in equation (11) and obtain the value of the energy 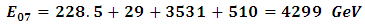
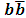 system [2, 3]
system [2, 3]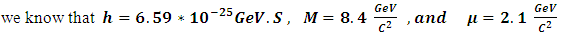 the coefficients of the potentials are as follows
the coefficients of the potentials are as follows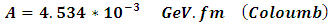
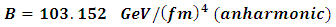
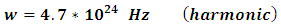
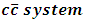 and
and 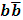 system. We chose the harmonic, an harmonic plus, Coulomb, potentials to solve the non-relativistic Schrodinger equation. The results give good agreement with the experimental data [9] with maximum error 2.8%
system. We chose the harmonic, an harmonic plus, Coulomb, potentials to solve the non-relativistic Schrodinger equation. The results give good agreement with the experimental data [9] with maximum error 2.8% 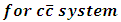 and 6.4%
and 6.4% 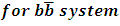 .
. Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML

