-
Paper Information
- Paper Submission
-
Journal Information
- About This Journal
- Editorial Board
- Current Issue
- Archive
- Author Guidelines
- Contact Us
Journal of Nuclear and Particle Physics
p-ISSN: 2167-6895 e-ISSN: 2167-6909
2015; 5(6): 97-100
doi:10.5923/j.jnpp.20150506.01

Theoretical Calculation of Plasma Thermal Energy Using the Solution of Equilibrium Problem
M. Asif
Department of Physics, COMSATS Institute of Information Technology, Lahore, Pakistan
Correspondence to: M. Asif, Department of Physics, COMSATS Institute of Information Technology, Lahore, Pakistan.
| Email: |  |
Copyright © 2015 Scientific & Academic Publishing. All Rights Reserved.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/

In this work we presented the plasma thermal energy by using the solution of equilibrium problem with Lithium limiter for circular cross-section HT-7 tokamak. For this, the poloidal beta was obtained by analytical solution of the Grad-Shafranov equation (GSE) and then the plasma thermal energy is calculated. It is observed, the plasma thermal energy obtained from the analytical solution of GSE by using liquid lithium limiter is larger than that using graphite limiter, which shows that the plasma performance was improved.
Keywords: Plasma, Thermal Energy, Equilibrium Problem
Cite this paper: M. Asif, Theoretical Calculation of Plasma Thermal Energy Using the Solution of Equilibrium Problem, Journal of Nuclear and Particle Physics, Vol. 5 No. 6, 2015, pp. 97-100. doi: 10.5923/j.jnpp.20150506.01.
Article Outline
1. Introduction
- In tokamaks the plasma configurations are described in terms of solutions of the Grad-Shafranov equation (GSE) [1-2]. Analytical solutions of the Grad-Shafranov [1-3] equation are very useful for theoretical studies of plasma equilibrium, transport and magnetohydrodynamic (MHD) stability. For tokamak operation, measurements of the poloidal beta
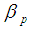 , plasma thermal energy and plasma temperature are important. Much more plasma parameters such as plasma confinement time, plasma current density profile, and magnetohydrodynamics (MHD) instabilities can be calculated.As we know confinement is limited by thermal conduction and convection processes, but radiation is also a source of energy loss. Since maximum energy confinement time is determined by the microscopic behavior of the plasma as collisions, and micro instabilities. Such kind of behavior ultimately leads to macroscopic energy transport which can be either classical or anomalous depending on the processes involved.In the absence of instabilities the confinement of toroidally symmetric tokamak plasma is determined by Coulomb collisions. Since these phenomena require knowledge of individual particle motion on short length and time scales, they are usually treated by kinetic models, but including only limited geometry because of the complexity of the physics. In the absence of a theoretical understanding of confinement, and given the need to predict the confinement properties of future tokamaks, it has been necessary to resort to empirical methods. The simplest of these is to accumulate data from a number of tokamaks, each operated under a range of conditions, and to use statistical methods to determine the dependence of the confinement time on the parameters involved. This provides scaling expressions which, within some error, allow extrapolation to projected tokamaks [1-15].Lots of lithium experiments have been carried out in tokamaks for the enhancement of plasma [4-11]. In this work we calculated the the plasma thermal energy by the Simplest Grad–Shafranov Equation (GSE) Solution [12] with Lithium limiter for Circular cross-section HT-7 tokamak. A generalized Grad-Shafranov-type equation [3], has been used. Specific functional forms of plasma internal energy and current are used. GSE is solved by considering linear source functions and fixed boundary conditions. For this, the poloidal beta [13, 14] was obtained from by analytical solution of GSE. Than we can find the plasma thermal energy [15]. It was clearly observed in [14] that the calculated internal inductance and the calculated poloidal beta depend on kind of discharge or plasma current.It is observed, the plasma thermal energy obtained from the analytical solution of GSE by using liquid lithium limiter is larger than that using graphite limiter, which shows that the plasma performance was improved. Also, the plasma thermal energy was measured using the diamagnetic loop [15].
, plasma thermal energy and plasma temperature are important. Much more plasma parameters such as plasma confinement time, plasma current density profile, and magnetohydrodynamics (MHD) instabilities can be calculated.As we know confinement is limited by thermal conduction and convection processes, but radiation is also a source of energy loss. Since maximum energy confinement time is determined by the microscopic behavior of the plasma as collisions, and micro instabilities. Such kind of behavior ultimately leads to macroscopic energy transport which can be either classical or anomalous depending on the processes involved.In the absence of instabilities the confinement of toroidally symmetric tokamak plasma is determined by Coulomb collisions. Since these phenomena require knowledge of individual particle motion on short length and time scales, they are usually treated by kinetic models, but including only limited geometry because of the complexity of the physics. In the absence of a theoretical understanding of confinement, and given the need to predict the confinement properties of future tokamaks, it has been necessary to resort to empirical methods. The simplest of these is to accumulate data from a number of tokamaks, each operated under a range of conditions, and to use statistical methods to determine the dependence of the confinement time on the parameters involved. This provides scaling expressions which, within some error, allow extrapolation to projected tokamaks [1-15].Lots of lithium experiments have been carried out in tokamaks for the enhancement of plasma [4-11]. In this work we calculated the the plasma thermal energy by the Simplest Grad–Shafranov Equation (GSE) Solution [12] with Lithium limiter for Circular cross-section HT-7 tokamak. A generalized Grad-Shafranov-type equation [3], has been used. Specific functional forms of plasma internal energy and current are used. GSE is solved by considering linear source functions and fixed boundary conditions. For this, the poloidal beta [13, 14] was obtained from by analytical solution of GSE. Than we can find the plasma thermal energy [15]. It was clearly observed in [14] that the calculated internal inductance and the calculated poloidal beta depend on kind of discharge or plasma current.It is observed, the plasma thermal energy obtained from the analytical solution of GSE by using liquid lithium limiter is larger than that using graphite limiter, which shows that the plasma performance was improved. Also, the plasma thermal energy was measured using the diamagnetic loop [15]. 2. Theoretical Equation
- The simplest solution of GSE can be found by assuming that [12],
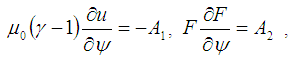 | (1) |
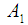 and
and 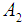 are constant. The internal energy in extended Grad-Shafranov equation [3] is a function of
are constant. The internal energy in extended Grad-Shafranov equation [3] is a function of 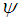 . The
. The 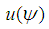 and
and 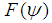 are two free functions, while
are two free functions, while 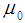 and
and 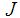 are the vacuum permeability and plasma current density respectively. This obviously reduces the set of possible current density profile shapes to
are the vacuum permeability and plasma current density respectively. This obviously reduces the set of possible current density profile shapes to 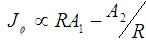 .If the plasma is assumed to be up–down symmetric, its shape can be described by four parameters. The equatorial innermost and outermost points,
.If the plasma is assumed to be up–down symmetric, its shape can be described by four parameters. The equatorial innermost and outermost points, 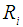 and
and 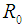 , and the coordinates of the highest point,
, and the coordinates of the highest point, 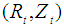 or equivalently, the major radius
or equivalently, the major radius 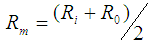 ,
, 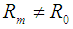 , the minor radius
, the minor radius 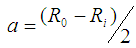 , the elongation
, the elongation 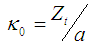 , and triangularity
, and triangularity 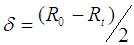 . The simplest solution is given by [12]
. The simplest solution is given by [12] | (2) |
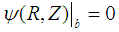 [16].With Eq. (2), the boundary conditions
[16].With Eq. (2), the boundary conditions 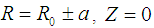 and
and 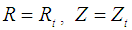 gives the following equations:
gives the following equations: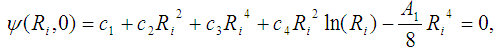 | (3) |
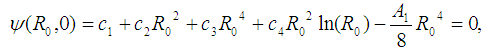 | (4) |
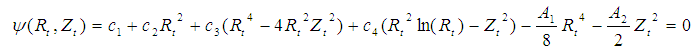 | (5) |
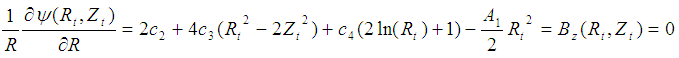 | (6) |
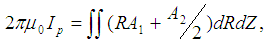 | (7) |
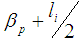 , because the parameter can be experimentally deduced using discrete magnetic probes [17], for circular cross section HT-7 tokamak [18],
, because the parameter can be experimentally deduced using discrete magnetic probes [17], for circular cross section HT-7 tokamak [18],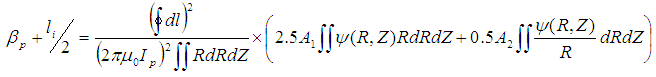 | (8) |
3. Calculation of Plasma Thermal Energy
- The six coefficients c1, c2, c3, c4, A1, A2 can be derived by solving equations [3-8]. So the poloidal magnetic flux
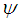 is obtained by substituting the six coefficients. According to the definition of the internal inductance [18]
is obtained by substituting the six coefficients. According to the definition of the internal inductance [18]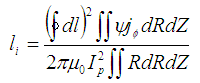 | (9) |
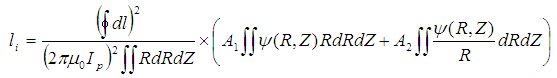 | (10) |
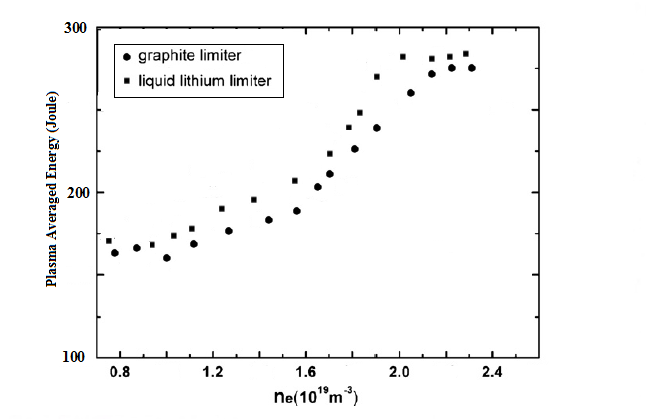 | Figure 1. Plasma Averaged Thermal Energy, obtained analytically by the solution of GSE as a function of line averaged electron density |
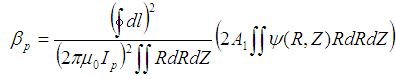 | (11) |
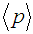 , and then the plasma thermal energy U.
, and then the plasma thermal energy U. 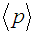 can be determined directly from the definition of the poloidal beta [18]:
can be determined directly from the definition of the poloidal beta [18]: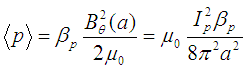 | (12) |
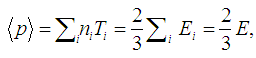 | (13) |
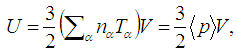 | (14) |
4. Result and Discussion
- Here we calculated the plasma thermal energy by the Simplest Grad–Shafranov Equation (GSE) Solution with Lithium limiter for circular cross-section HT-7 tokamak. GSE is solved by considering linear source functions and fixed boundary conditions. For this, the poloidal beta [13, 14, 18] was obtained by analytical solution of GSE and then the plasma thermal energy is calculated. It was clearly observed in [14] that the calculated internal inductance and the calculated poloidal beta depend on kind of discharge or plasma current. It is observed, the plasma thermal energy obtained from the analytical solution of GSE using liquid lithium limiter is larger than that using graphite limiter, which shows that the plasma performance was improved. These parameters included the poloidal beta and plasma thermal energy can be measured by experimental method based on a diamagnetic effect [11, 15, 17].
 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML