-
Paper Information
- Paper Submission
-
Journal Information
- About This Journal
- Editorial Board
- Current Issue
- Archive
- Author Guidelines
- Contact Us
Journal of Nuclear and Particle Physics
p-ISSN: 2167-6895 e-ISSN: 2167-6909
2015; 5(4): 84-87
doi:10.5923/j.jnpp.20150504.03
A Preliminary Explanation for the Pentaquark 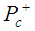 Found by LHCb
Found by LHCb
Mario Everaldo de Souza
Departamento de Física, Universidade Federal de Sergipe, Av. Marechal Rondon, s/n, Rosa Elze, São Cristóvão, SE, Brazil
Correspondence to: Mario Everaldo de Souza, Departamento de Física, Universidade Federal de Sergipe, Av. Marechal Rondon, s/n, Rosa Elze, São Cristóvão, SE, Brazil.
| Email: |  |
Copyright © 2015 Scientific & Academic Publishing. All Rights Reserved.
We propose that the two resonant states of the recently found pentaquark 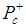 with masses of 4380 MeV and 4450 MeV are two states of the hadronic molecule
with masses of 4380 MeV and 4450 MeV are two states of the hadronic molecule 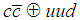 with similar properties to those of the Karliner-Lipkin pentaquark. Applying the Morse molecular potential to the molecule its minimum size is estimated. If S states exist, the first two possible S states are suggested and their energies are estimated. It is shown that the coupling constant is close to that of charmonium, and this may mean Physics Beyond the Standard Model.
with similar properties to those of the Karliner-Lipkin pentaquark. Applying the Morse molecular potential to the molecule its minimum size is estimated. If S states exist, the first two possible S states are suggested and their energies are estimated. It is shown that the coupling constant is close to that of charmonium, and this may mean Physics Beyond the Standard Model.
Keywords: Pentaquark, Charmonium-pentaquark
Cite this paper: Mario Everaldo de Souza, A Preliminary Explanation for the Pentaquark 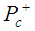 Found by LHCb, Journal of Nuclear and Particle Physics, Vol. 5 No. 4, 2015, pp. 84-87. doi: 10.5923/j.jnpp.20150504.03.
Found by LHCb, Journal of Nuclear and Particle Physics, Vol. 5 No. 4, 2015, pp. 84-87. doi: 10.5923/j.jnpp.20150504.03.
Article Outline
1. Introduction
- The idea of the pentaquark was firstly proposed by Strottman in 1979 [1]. In 2004 Karliner and Lipkin proposed a very important model for a pentaquark in the description of the
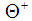 [2]. They arrived at the conclusion that the bag model commonly used for hadrons may not be adequate for the pentaquark. In their model they propose that the pentaquark system is composed of two clusters, a diquark and a triquark, in a relative P-wave state. The clusters in this system can be separated by a distance larger than the range of the color-magnetic force which had been proposed by De Rujula, Georgi and Glashow [3]. It is important to recall that many authors have considered the possibility of binding between
[2]. They arrived at the conclusion that the bag model commonly used for hadrons may not be adequate for the pentaquark. In their model they propose that the pentaquark system is composed of two clusters, a diquark and a triquark, in a relative P-wave state. The clusters in this system can be separated by a distance larger than the range of the color-magnetic force which had been proposed by De Rujula, Georgi and Glashow [3]. It is important to recall that many authors have considered the possibility of binding between 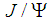 and nuclei. Among them we can cite [4-11]. They have raised some important observations concerning the interaction such as that meson exchange is suppressed by the OZI rule because
and nuclei. Among them we can cite [4-11]. They have raised some important observations concerning the interaction such as that meson exchange is suppressed by the OZI rule because 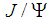 and nuclei do not have quarks in common and also single gluon exchange is forbidden so that the interaction should happen due to multiple-gluon exchange. The LHCb Collaboration has recently [12] announced the discovery of pentaquark-charmonium states which resulted from the
and nuclei do not have quarks in common and also single gluon exchange is forbidden so that the interaction should happen due to multiple-gluon exchange. The LHCb Collaboration has recently [12] announced the discovery of pentaquark-charmonium states which resulted from the 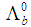 exotic decay
exotic decay 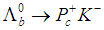 , in which
, in which 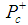 is a pentaquark with the quark content
is a pentaquark with the quark content 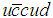 . The two resonant states have masses of about 4380 MeV and 4450 MeV in opposite parities with the preferred values for
. The two resonant states have masses of about 4380 MeV and 4450 MeV in opposite parities with the preferred values for 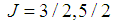 and with the corresponding
and with the corresponding 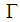 ’s of
’s of 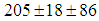 MeV and
MeV and 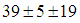 MeV. All the data for the masses below were taken from the Particle Data Group [13].
MeV. All the data for the masses below were taken from the Particle Data Group [13].2. A Simple Model for the LHCb 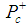
- We propose that the recently found LHCb
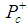 is composed of two colorless clusters, a meson and a baryon. The quark content of the
is composed of two colorless clusters, a meson and a baryon. The quark content of the 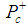 pentaquark,
pentaquark, 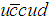 allows the two possibilities
allows the two possibilities 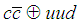 and
and 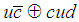 , but as the final decay is
, but as the final decay is 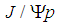 we should rule out the second possibility. The symbol
we should rule out the second possibility. The symbol  is used to designate the binding between the two clusters. According to QCD, we expect the two clusters to be weakly bound because hadrons are colorless. The most famous hadronic molecule is the deuteron, also constituted of colorless particles. Because the two particles (nucleons) are colorless the binding is very weak, just about 2.2 MeV. But in the case of the
is used to designate the binding between the two clusters. According to QCD, we expect the two clusters to be weakly bound because hadrons are colorless. The most famous hadronic molecule is the deuteron, also constituted of colorless particles. Because the two particles (nucleons) are colorless the binding is very weak, just about 2.2 MeV. But in the case of the 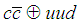 we do not know what kind of binding energy we have. Between two nucleons the nuclear force is a residual effect of the more fundamental forces of the color field in the quark systems, but we still do not know the nature of the force responsible for the binding between
we do not know what kind of binding energy we have. Between two nucleons the nuclear force is a residual effect of the more fundamental forces of the color field in the quark systems, but we still do not know the nature of the force responsible for the binding between 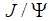 and the proton in the molecule
and the proton in the molecule 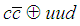 . We can estimate below the minimum value for the binding energy.
. We can estimate below the minimum value for the binding energy.3. Possibilities for the Angular Momenta
- As the final decay is
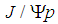 we should consider the two possibilities for the molecule:
we should consider the two possibilities for the molecule: 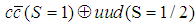 and
and 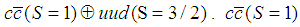 is J/Psi and
is J/Psi and 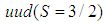 is the resonance N(1520) whose mass is actually about 1515 MeV. The sum of the masses 3096 MeV+1515 MeV = 4611 MeV is much higher than 4380 MeV and 4450 MeV. Therefore, we should consider only the first possibility. In order to reproduce the experimental values of
is the resonance N(1520) whose mass is actually about 1515 MeV. The sum of the masses 3096 MeV+1515 MeV = 4611 MeV is much higher than 4380 MeV and 4450 MeV. Therefore, we should consider only the first possibility. In order to reproduce the experimental values of 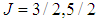 we should have
we should have 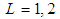 for the molecule. Taking into account the Karliner-Lipkin model [2] in which the clusters are in a relative P-wave state, we can propose that the levels found by LHCb for the
for the molecule. Taking into account the Karliner-Lipkin model [2] in which the clusters are in a relative P-wave state, we can propose that the levels found by LHCb for the 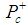 system are in relative P-wave and D-wave states. The possibility of S states is discussed below, in section V.Let us now analyze the angular momenta of the molecule
system are in relative P-wave and D-wave states. The possibility of S states is discussed below, in section V.Let us now analyze the angular momenta of the molecule 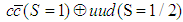 and its components. Composing the two spins we obtain
and its components. Composing the two spins we obtain 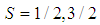 . With
. With 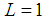 and
and 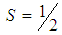 we have
we have 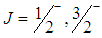 , and for
, and for 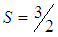 we have
we have 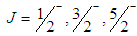 . With
. With 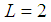 and
and 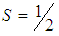 we have
we have 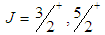 , and for
, and for 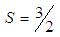 we have
we have 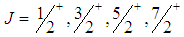 . We see that the most favored values for
. We see that the most favored values for 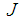 are
are 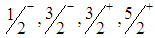 .
.4. The Approximate Size of the Molecule
- We have no idea yet on the kind of effective potential that exists in the
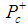 system. Assuming that there is a potential well we may model the system through a molecular potential and obtain some important numbers. It is important to notice that the components of the system are heavy and, thus, we can use the Schrödinger equation in the description of the system. Recently, de Souza [14, 15] has used the Morse molecular potential in the description of charmonium and bottomonium states. The Morse molecular potential can be expressed as [16]
system. Assuming that there is a potential well we may model the system through a molecular potential and obtain some important numbers. It is important to notice that the components of the system are heavy and, thus, we can use the Schrödinger equation in the description of the system. Recently, de Souza [14, 15] has used the Morse molecular potential in the description of charmonium and bottomonium states. The Morse molecular potential can be expressed as [16]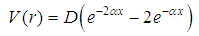 | (1) |
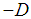 is the minimum of the well, a is the distance where
is the minimum of the well, a is the distance where 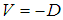 , and
, and 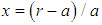 .For
.For 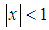 this potential can be expanded around the minimum up to order 3 in
this potential can be expanded around the minimum up to order 3 in 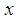 and the expression
and the expression 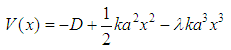 | (2) |
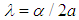 .For this potential the solution of the Schrödinger equation yields the expression [16, 17]
.For this potential the solution of the Schrödinger equation yields the expression [16, 17]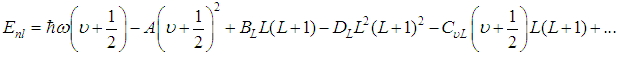 | (3) |
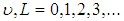 In Eq. 3 the first term describes harmonic vibrations, the second term takes into account the anharmonicity of the potential, the third term describes rotations with constant moment of inertia, the fourth term represents the centrifugal distortion and the fifth term represents the coupling between vibration and rotation. The constant
In Eq. 3 the first term describes harmonic vibrations, the second term takes into account the anharmonicity of the potential, the third term describes rotations with constant moment of inertia, the fourth term represents the centrifugal distortion and the fifth term represents the coupling between vibration and rotation. The constant 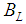 is given by
is given by 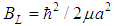 where
where 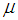 is the reduced mass of the system.In the case of
is the reduced mass of the system.In the case of 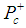 we only have two levels, one for L=1 and another for L=2 for
we only have two levels, one for L=1 and another for L=2 for 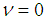 in Eq. 3 Therefore we can only determine two parameters of the above formula. The largest parameters in Eq. (3) are
in Eq. 3 Therefore we can only determine two parameters of the above formula. The largest parameters in Eq. (3) are 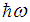 and
and 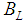 . In general
. In general 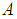 is not very small compared with
is not very small compared with 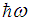 , but for
, but for 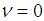 the 2nd term is
the 2nd term is 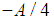 while the first one is
while the first one is 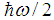 , and thus, the first term has a much larger contribution than the 2nd term. Moreover, the inclusion of
, and thus, the first term has a much larger contribution than the 2nd term. Moreover, the inclusion of 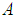 would not change the value of
would not change the value of 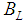 in our fitting because the two levels 4380 MeV and 4450 MeV have
in our fitting because the two levels 4380 MeV and 4450 MeV have 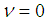 . The inclusion of
. The inclusion of 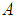 would increase slightly the value of
would increase slightly the value of 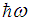 . The 4th and 5th terms are much smaller than the 3rd term. So, due to lack of data we can only have
. The 4th and 5th terms are much smaller than the 3rd term. So, due to lack of data we can only have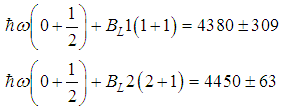 | (4) |
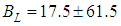 MeV and
MeV and 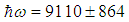 MeV. Using the relation
MeV. Using the relation 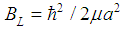 we find
we find 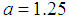 fm but with a large uncertainty due to the large uncertainty of
fm but with a large uncertainty due to the large uncertainty of 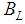 .There are some available data for the radii of the proton and charmonium that allows us to have more information on the molecule
.There are some available data for the radii of the proton and charmonium that allows us to have more information on the molecule 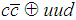 . The size of
. The size of 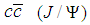 is about
is about 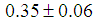 fm [15] and the proton radius (charge radius) has been reported as being 0.8879 fm [18], 0.8775 fm [19], and 0.84087 fm [20, 21]. Summing the radii of
fm [15] and the proton radius (charge radius) has been reported as being 0.8879 fm [18], 0.8775 fm [19], and 0.84087 fm [20, 21]. Summing the radii of 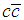 and the proton we obtain about 1.2 fm which is very close to the value of
and the proton we obtain about 1.2 fm which is very close to the value of 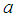 . But
. But 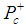 in states with L=1 and L=2 is larger than 1.25 fm, of course, because the wave functions of L states contain the term
in states with L=1 and L=2 is larger than 1.25 fm, of course, because the wave functions of L states contain the term 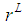 . It is only worth making the calculation when we obtain a much smaller value for the
. It is only worth making the calculation when we obtain a much smaller value for the 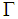 of the 4380 MeV level, and thus, as a consequence, a more precise value for
of the 4380 MeV level, and thus, as a consequence, a more precise value for 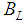 .
.5. The First Levels of the Molecule 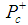
- In our model above
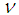 corresponds to
corresponds to 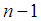 in QCD models, that is, n=
in QCD models, that is, n=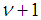 . Thus, the two states 4380 MeV and 4450 MeV are the states
. Thus, the two states 4380 MeV and 4450 MeV are the states 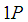 and
and 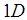 , respectively.As we saw above we could not calculate the value of
, respectively.As we saw above we could not calculate the value of 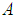 whose inclusion would increase slightly the value of
whose inclusion would increase slightly the value of 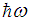 . This means that
. This means that 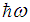 is a little larger than 9110 MeV. As
is a little larger than 9110 MeV. As 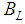 is very small (
is very small (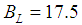 MeV) and is, indeed, much smaller than the
MeV) and is, indeed, much smaller than the 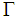 of the level 4380 MeV which is
of the level 4380 MeV which is 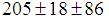 MeV, if the
MeV, if the 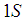 level exists, it would have an energy around 4.3 GeV. This would explain why the level 4380 MeV is much broader than the 4450 MeV level, and would mean that the 4380 MeV level is, actually, degenerate levels
level exists, it would have an energy around 4.3 GeV. This would explain why the level 4380 MeV is much broader than the 4450 MeV level, and would mean that the 4380 MeV level is, actually, degenerate levels 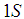 and
and 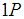 . Of course, considering the spins of
. Of course, considering the spins of 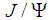 and the proton, the values of
and the proton, the values of 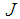 for
for 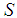 states would be only
states would be only 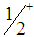 and
and 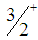 . By the same token, if the state
. By the same token, if the state 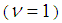 exists, it would have an energy around
exists, it would have an energy around 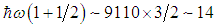 GeV. Thus we can propose that, if S states exist, the LHCb pentaquark would have the levels shown in Table 1.
GeV. Thus we can propose that, if S states exist, the LHCb pentaquark would have the levels shown in Table 1.
|
6. The Binding Energy and the Coupling Constant
- For a square well we have that in order to have a bound state (for an S wave) we should have a depth of
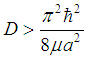 | (5) |
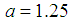 fm and
fm and 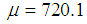 MeV yields
MeV yields 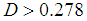 Mev. The coupling constant is not small at all. From the value of
Mev. The coupling constant is not small at all. From the value of 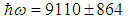 MeV we obtain
MeV we obtain 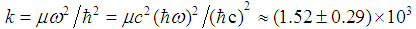 GeV/fm2 which is close to that for charmonium,
GeV/fm2 which is close to that for charmonium, 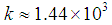 GeV/fm2 [15]. Taking into account the OZI rule, we can say that such a strong coupling may be due to Physics Beyond the Standard Model.
GeV/fm2 [15]. Taking into account the OZI rule, we can say that such a strong coupling may be due to Physics Beyond the Standard Model.7. Conclusions
- It is proposed that the observed levels of the recently found pentaquark
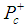 are states of the molecule
are states of the molecule 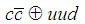 in the different relative angular momentum
in the different relative angular momentum 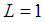 and
and 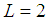 states, and is similar to the pentaquark system proposed by Karliner and Lipkin [2]. It is shown how the observed angular momenta are generated, and an approximate minimum value for the size of the molecule is calculated. It is shown that the coupling constant is not small and has the same order of magnitude of that for charmonium. This may mean Physics Beyond the Standard Model. Possible S states are proposed for the system and their energies are estimated.Although still preliminary, the work is relevant and shows a consistent possibility for this recently discovered system of 5 quarks. More data is needed to improve the model and calculate other parameters of Eq. 3. It is important to find out, for example, if the system has or not excited states. This paper should be taking as one of the starting points for understanding this remarkable system.
states, and is similar to the pentaquark system proposed by Karliner and Lipkin [2]. It is shown how the observed angular momenta are generated, and an approximate minimum value for the size of the molecule is calculated. It is shown that the coupling constant is not small and has the same order of magnitude of that for charmonium. This may mean Physics Beyond the Standard Model. Possible S states are proposed for the system and their energies are estimated.Although still preliminary, the work is relevant and shows a consistent possibility for this recently discovered system of 5 quarks. More data is needed to improve the model and calculate other parameters of Eq. 3. It is important to find out, for example, if the system has or not excited states. This paper should be taking as one of the starting points for understanding this remarkable system. Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML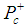 if S states exist
if S states exist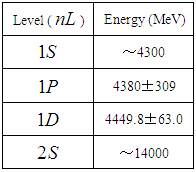
 ,
,  and
and 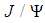 mesons in nuclei, arXiv0907.0244.
mesons in nuclei, arXiv0907.0244.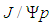 resonances consistent with pentaquark states in
resonances consistent with pentaquark states in 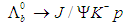 decays, arXiv: 1507.03414; Phys. Rev. Lett. 115, 072001, 2015.
decays, arXiv: 1507.03414; Phys. Rev. Lett. 115, 072001, 2015.