1. Introduction

Mass-energy equivalence is a central principle of fundamental physics. The mathematical formalism of the process is well-established, at least at the level of the inputs and outputs. However the workings of the process at the particle level are obscure, and this is the subject of the present paper. There are two directions to the process, one being the conversion of energy into a particle-antiparticle pair (pair production), and the other the conversion of matter-antimatter pairs into energy (annihilation). The area under examination in this paper is the pair production process, and a non-local hidden-variable (NLHV) theory is applied to elicit a proposed explanation of the process.

Pair production is the process of creating a particle-antiparticle pair from photon energy [1]. A common process is two photons producing an electron and positron (antielectron). Other possible outcomes include muon and tau pairs, and the elementary fermions (quarks and leptons) generally. In all cases there needs to be enough energy in the system to produce those pairs, which for an electron at rest is 0.511 MeV, with the same again required for producing the antielectron. The pair production process may occur with a single (high energy) photon interacting with a nucleon (thereby providing a platform for conservation of momentum), or two photons interacting together. Pair production is an important process among the many others that occur in high-energy collisions involving atoms [2]. It affects other processes such as ionization. Furthermore, it contributes to energy loss in these impact situations, and also in supernovae.

Historically the primary research interest in pair-production has been the development of models for the outputs of the process for given input energy and situational variables, e.g. [3]. This has generally been successful and current models permit an accurate prediction of outputs [4], as well as insights into the identities of the variables and the mathematical relationships between them. The outputs of the process are modelled adequately by quantum field theory (QFT). These existing approaches to understanding mass-energy equivalence are invariably based on representing what happens, via mathematical quantification of the process as a whole.

However there is an unanswered ontological question of how the internal sub-processes operate at the next deeper foundational level, particularly how the photons transform into matter-antimatter pairs.

Before showing a solution to this problem, it is necessary to identify why this is even a valid question to ask. The issue is that it is not clear, from the perspective of quantum mechanics (QM), why there should be a necessity for a physical mechanism underpinning pair production. Quantum theory is premised on particles being zero-dimensional (0-D) points. Hence it is meaningless from within that framework for particles to have internal structures or inner processes. Instead the QM perspective is that a point photon splits into a point electron and positron, merely by partitioning the energy and quantum numbers. Such an interpretation is to be expected, being merely self-consistent with the 0-D point premise that underpins quantum theory. As has abundantly been shown by the Bell-type inequalities, the idea that particles may have internal structures is fundamentally incompatible with the 0-D point premise of quantum theory.

Consequently the question of how the internal processes operate for pair-production is only nonsensical from the perspective of quantum mechanics. For theories where particules have internal structure, e.g. the NLHV solutions, the question is meaningful. This paper applies a specific NLHV solution, in the form of the Cordus theory, to the problem. It predicts the field transformations that would be necessary to convert a photon into a matter-antimatter pair. The specific area under examination is the creation of an electron-antielectron pair from two photons. The current work is part of a broader theory of fundamental physics that is distinct to, and positioned deeper than, quantum theory. The two should not be confounded.

The idea of particles being zero-dimensional points is not a fundamental requirement of physics, but merely a construct of quantum theory. Hence it is worth exploring the conceptual implications of alternative theories that are not based on the 0-D point constraint. At this early stage of the development of the alternative theory the exposition is primarily conceptual. Thus the reader will not here find a mathematical formalism or quantitative model of pair-production cross sections.

2. Existing Approaches

Where two photons are involved, quantum electrodynamics (QED) assumes that photons do not couple directly with each other, but instead one of the photons spontaneously fluctuates into a particle-antiparticle pair, and the other photon is absorbed into (couples to) one of those particles (two-photon physics). The fluctuation is held to be a random event driven by the Heisenberg uncertainty principle. The particle-antiparticle pair is thought to comprise leptons or quarks, and their antiparticle, e.g. pion or kaon pairs. Feynman diagrams may be used to represent the input and output components of pair production.

The theoretical aspect of pair production that has received the most attention is the prediction of the relative likelihood of specific outcomes compared to others, with photons of different energy, hence cross section. Within that a particular focus area is the impact of a photon on an atom. Pair-production is one of several possible outcomes in such cases, others being Compton scattering, and energy absorption, depending on the energy of the photon. At high energy the pair-production process dominates. This is commonly modelled as a perturbation interaction between the photon and an unbound electron described in plane waves, hence the Bethe-Heitler process [5]. The probability of pair-production occurring for various input energies is then determined, and this is the cross section σ. This may then be compared to empirical results. Typical features of the relationship are that pair-production only occurs above a threshold photon energy, and becomes steadily more likely as energy increases, before becoming constant as the process saturates [4]. Additional complexities arise with the electron being bound in an atom, and a screened vs. bare nucleus. The cross sections depend on the atomic number of the target. A close match to empirical results is obtained for light and heavy lepton production, though a number of other coefficients and tuning factors are required [2].

Pair production may also occur by the collision of two photons [6] (Breit-Wheeler model). Another production mechanism is collision of electron and laser beams, which involves additional mechanics due to the multiphoton collisions and interactions of daughter products with the beams [7]. Other situations that have been modelled include muons [8] and the inverse Cerenkov process [9]. Another area of complementary research is the creation of electron and electron-hole pairs in solids [10], with the input energy being plasmons as opposed to photons. Almost all the recent progress has focussed on developing more refined mathematical models with better fit to empirical results.

A deeper explanatory understanding of the mechanics is altogether lacking. More specifically, although the current models describe what happens, the how is not described. For example, the Breit-Wheeler model describes the evolution of the electron pair as something that merely appears in the mathematics, that 'one finds that at a time t … the wave function contains a term which may be interpreted as referring to an electron '[6]. This is totally unsatisfactory from an ontological perspective, more so from the basis of physical realism, and this deficiency has long been identified. As Dirac observed, QM has the characteristic whereby it is ‘usually easier to discover the equations that describe some particular phenomenon than just how the equations are to be interpreted’ [11]. Others have continue to press the point that there are interpretational difficulties with the mathematical solutions for pair production [12]. Currently mathematical models, despite their excellence in identifying the relationships between variables and predicting the outputs, have no explanatory power. Furthermore they are approximations that treat particles en-masse in the form of beams (multi-photons). They do not address the discrete individual interactions between photons and matter [12].

There presumably must be substantial changes required to convert a photon into an electron. Apparently a photon does not simply halve itself to make an electron-antielectron pair. Or if it does, the conditions under which it does this are not evident. Part of the problem is that QM and the Standard Model assume that particules are zero-dimensional points, without internal structure. All the many variables that a particule is known to have, such as charge, spin, mass, are considered to be abstract intrinsic variables. This rejection of inner structure makes it impossible to contemplate pair-production as involving the remanufacture of internal structure, at least not from within the quantum theory. Yet QM has no alternative explanation to offer. The situation is therefore an ontological singularity for QM. At the same time the Standard Model proposes that all interactions occur via exchange of specialised messenger particles, the gauge bosons, with that for electro-magnetism being the photon. So the photon has a dual and potentially conflicted role of being both the messenger particle, and the source for pair production, and it is unclear how those roles are differentiated.

Thus the mechanisms for converting a photon into a matter-antimatter pair are unknown. This is an obstacle to the understanding of many phenomena in fundamental physics, including asymmetrical genesis: if we do not understand the first stage of conversion into particle-antiparticle pairs, then it is going to be difficult to find where the asymmetry occurs. There is a need for theories that better explain the pair-production processes.

3. Purpose and Approach

The purpose of this work was to explore the feasibility of explaining pair-production from the non-local hidden-variable (NLHV) sector. This may not seem a promising sector in which to prospect for foundational solutions, given that it has historically included only one serious candidate, the de-Broglie-Bohm theory [13, 14] which has not progressed far. Furthermore, the Bell type inequalities [15-17] preclude local hidden-variable solutions, at least for 0-D point particles like those assumed for quantum mechanics. While no mathematical proof has yet excluded all non-local hidden-variable solutions, there is the practical problem that the sector has failed to provide new candidate solutions for evaluation. Consequently the whole hidden-variable sector is generally considered either non-viable or at least non-productive.

Nevertheless the hidden variable sector has potential, as demonstrated in recent developments of the Cordus theory [18]. This is a NLHV candidate solution, with a specific design of internal structures. It has been used to explain many fundamental phenomena including wave-particle duality, unification, nuclides (H to Ne), and time [18-21].

The approach in the present paper started with the NLHV design of the Cordus theory, specifically the matter-antimatter species differentiation [22], and the annihilation mechanisms [23]. These explanations were based on the concept that the nature of a particule, electron, photon, etc., is determined by its characteristic field structures, which are proposed to be discrete. The re-allocation of these discrete forces has been used to explain the annihilation process [23]. The Cordus theory also has a methodology called HED mechanics that represents the principles for conservation and transformation of discrete fields, hence transmuting the identity of particles [24]. The name arises as it represents the states of the discrete fields or hyperfine fibril emission directions (HEDs). The present paper applies the same principles to the pair production situation.

4. Results

The present work is a logical extension of a prior concept for a NLHV design, and this is briefly explained first. Then we explain the proposed mechanics for manipulating discrete force structures, followed by application to the pair-production situation.

4.1. Cordus Theory

The Cordus theory has been described elsewhere [24], and is only briefly summarised here. The core conjecture is that all particles have inner and outer structures comprising two reactive ends some distance apart (span), connected by a fibril (hence cordus), and emitting discrete forces [18]. This is called a particule to differentiate it from the zero-dimensional (0D) point idea of quantum mechanics. The fibril is a persistent structure that provides instantaneous connectivity and synchronicity between the two reactive ends, but does not interact with matter. The reactive ends are energised sequentially (at the de Broglie frequency), during which they emit discrete forces out into the external environment. The locus of these over time defines a type of flux line called a hyperfine fibril (hence hyff). The discrete forces are emitted in three spatial directions (hence hyff emission directions, HEDs), and hence space is filled with a fabric of discrete forces [25]. The quantity, direction, and arrangement of these discrete forces determine the type of particule and are responsible for charge, mass, matter-antimatter species differentiation, and spin [22]. The discrete forces are responsible for the electro-magneto-gravitational and strong interactions, though the theory uses the term synchronous interaction in place of the strong, as this better describes the proposed nature of the interaction [19].

The resulting structures of the photon, electron, and antielectron (positron) are shown in Figures 1-3. Why these specific structures, as opposed to others? These are simply the structures that emerged from the systems design approach. The systems approach was underpinned by the premise that physical realism prevails (physical phenomena have physical causality). The process took known functionality of the system (e.g. the empirical evidence of fundamental physics in the double slit device), and then applied an iterative creative process to infer the inner structures that would be necessary and sufficient to explain those behaviours. This is an independent ex nihilo conceptual process that is not reliant on precursor concepts from prior theories of physics. The figures show the particle designs that emerged.

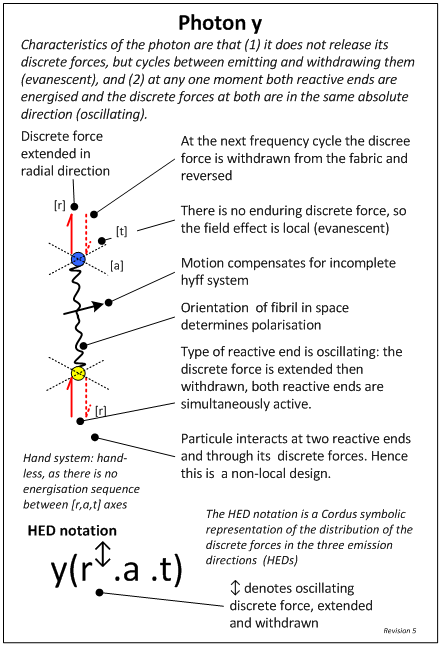Figure 1. Predicted inner structures of the photon in the Cordus theory. From [23] with permission

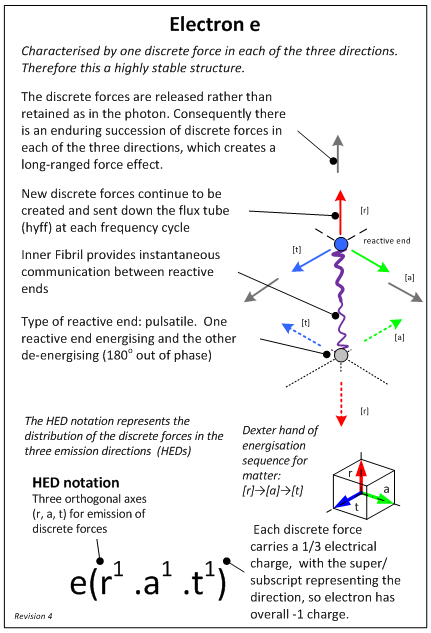Figure 2. Predicted inner structures of the electron. From [23] with permission

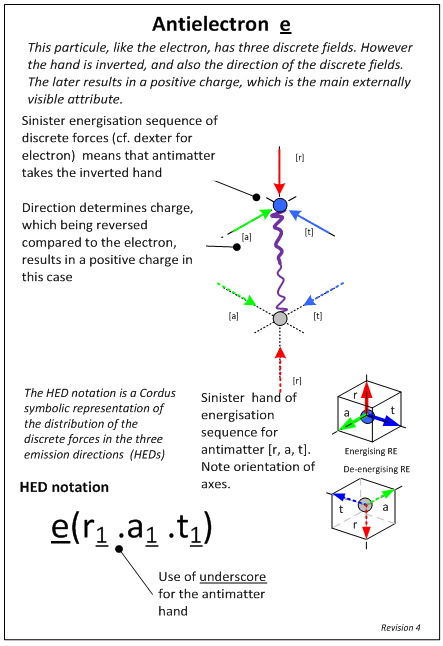Figure 3. Predicted inner structures of the antielectron. From [23] with permission

At this point a potential objection arises to the Cordus theory. This is that QCD can give rise to a flux tube but would not give rise to the proposed electron two-ended structure nor permit the proposed instantaneous communication between the spatially separated ends. The rebuttal is that the Cordus theory is not a version of quantum mechanics, and is not limited by what is admissible according to QCD or QFT. This is an unorthodox physics based on a NLHV design underpinned only by the premise of physical realism.

Recovery of the evanescent and electrostatic fields

Note the specific differences in the behaviour of the discrete forces between the photon and electron, as this is important in what follows. The photon emits and withdraws its discrete force in an oscillating manner. Consequently the field of the photon recruits a volume of space, which is consistent with the observation that the evanescent field scales as e^-r. The electron, in contrast, is proposed here to continue to emit new discrete forces outwards. Therefore its field dilutes over the area of a sphere. This too is consistent with the observation that the electro-magneto-gravitational (EMG) fields scales as r^-2. So the Cordus theory recovers both the evanescent field of the photon and the electrostatic field of the electron.

Thus the nature of discrete forces emitted by the photon and electron are proposed to be very different. This begins to explain why the photon and electron do not spontaneously transform from one to the other: they are not similar states that can randomly jump from one to the other in some Markov-like process. The next challenge is to explain how the transformation occurs.

4.2. Production of an Electron-Antielectron Pair

Here we show how photons may be converted to an electron and antielectron. We represent this in two ways, first by considering the interactions of individual discrete forces, and then using HED notation.

The overall process is shown in Figure 4. This is a systems engineering representation in integration definition zero (IDEF0) notation [26] and shows a process with inputs at left of the activity block, outputs at right, and mechanisms entering from beneath.

Pair production is commonly represented as starting with a single photon interacting with matter, hence the processes of photon absorption (6) and emission (7) per Figure 4. The absorption and emission interactions with matter have been represented in the NLHV framework of the Cordus theory [27]. Therefore we can put aside the initial matter interaction, and focus on the subsequent transformation processes. The main pair production activities therefore start with two separate photons. As per the Cordus theory these have the oscillating type of reactive ends. The reactive ends of the two photons are close together (1, Fig.4). The proximity causes distress in access to emission directions (HEDs), and the reactive ends respond to these constraints (2, Fig. 4). The mechanism by which they achieve this is renegotiation of emission directions. This requires the discrete forces and hence reactive ends, to change to accommodate. This is an application of the synchronous interaction (strong force) [19]. The reactive ends then develop 3D HED structures (3, Fig.4) in the [r, a, t] directions. Since HED emissions define the type of particule, new particule identities emerge as a consequence (4, Fig.4). The discrete field structures separate into complementary hands, matter and antimatter [22]. This is driven by stability requirements. Consequently handed discrete force structures emerge, and these are the antielectron and electron (5, Fig. 4) as will be shown.

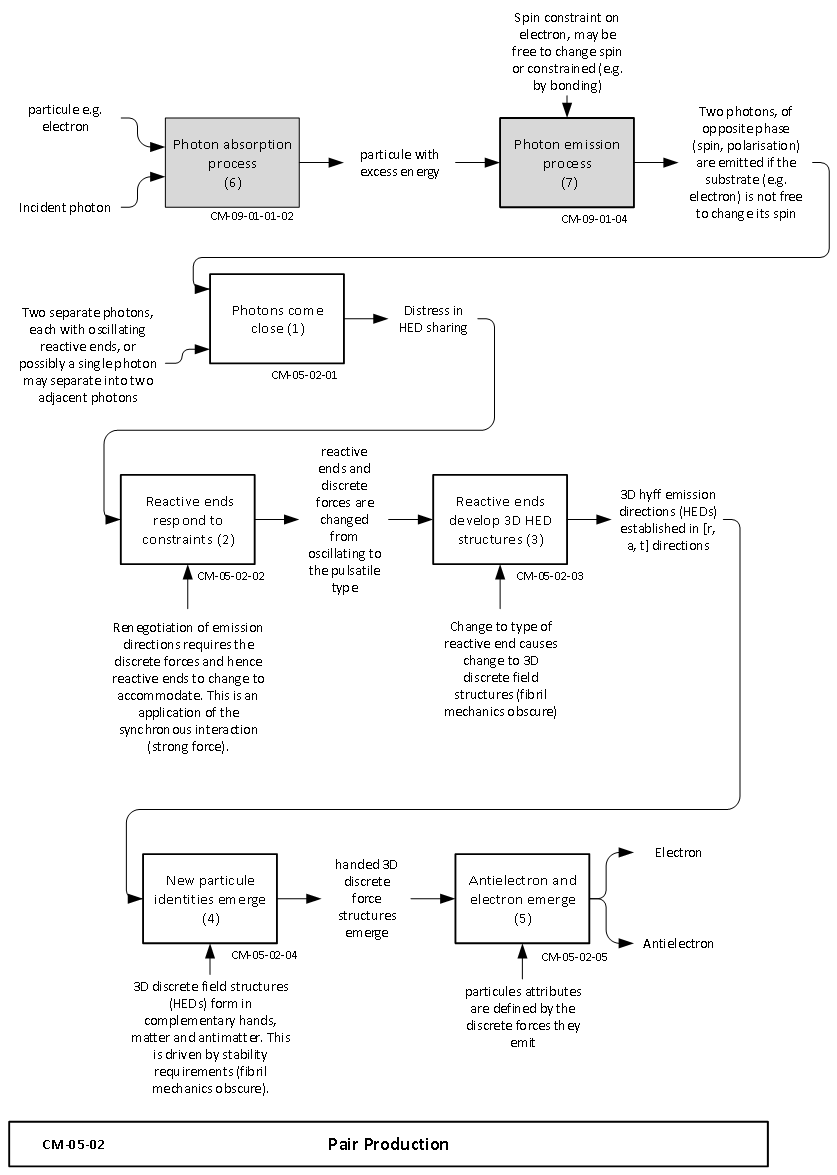Figure 4. Activities in the pair-production process

The process is further detailed at the level of discrete forces, in Figures 5 and 6 which show the proposed three-dimensional (3D) field-model. In essence, the incoming photons are unable to negotiate shared use of the field emission directions (1.3, Fig.5). Their difficulty is that the oscillating discrete forces are simultaneously active at all reactive ends, and are trying to recruit the same volume of space. To put it another way, the evanescent fields are in conflict. Nor can the photons evade each other. So they are forced to convert to the pulsatile type of reactive end instead (2.1, Fig.5). This type has one reactive end active and the other dormant, and it emits and releases its discrete forces (as opposed to recruiting a volume of space), so it is much easier to satisfy the constraints. The process also creates a new fibril to coordinate the new pairs of reactive ends (2.2, Fig.5). This type also requires three emission directions, so a 3D field structure is set up (3.1, Fig.5) according to the matter-antimatter hand system (4.1, Fig.6) [22]. The particule identities, electron and antielectron, emerge as a consequence of the changes to the discrete force structures (5.1, 5.2, Fig.6).

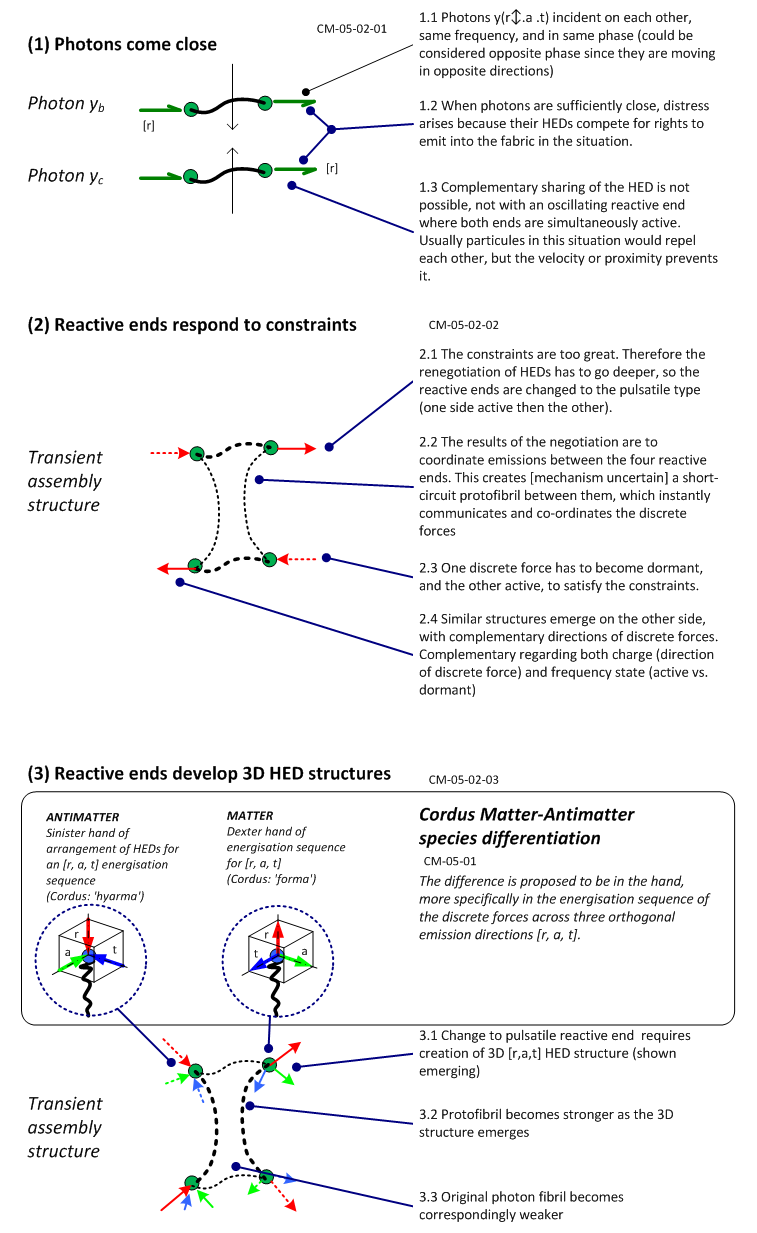Figure 5. Details of the proposed discrete force remanufacturing processes in the initial stages of pair production

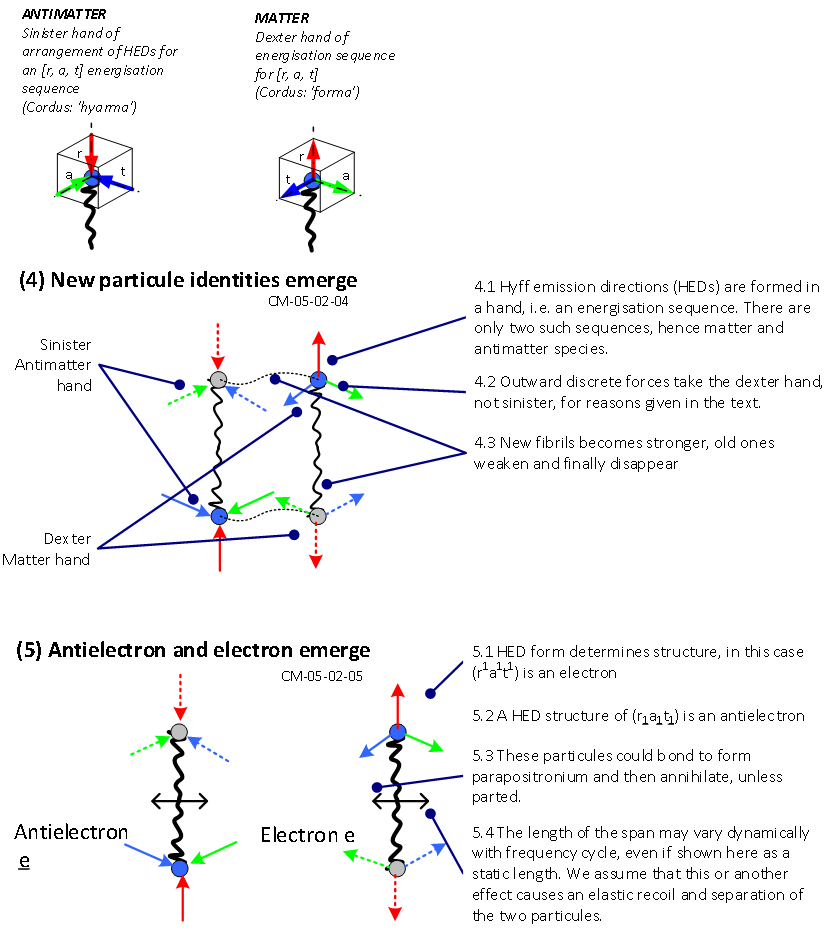Figure 6. Discrete force remanufacturing processes proposed for the later stages of pair production

Examining the remanufacturing process at the level of discrete forces is interesting, and shows that it is possible to provide a natural explanation for pair production. However it is also useful to have a simplified representation of the process, which we provide next.

4.3. Simplified Representation of Pair Production

Here we show a simpler and more efficient means of representing the process of pair production, using HED mechanics and its notation [24]. This is a mathematical formalism for the discrete fields in the Cordus theory. The notation represents the type of discrete field (oscillating or pulsatile), the number of discrete fields in each of the three orthogonal directions (r, a, t), the charge (superscript for negative, subscript for positive), the matter-antimatter species differentiation (plain text or underscore respectively). See Figures 1-3 for the HED notation for the photon, electron, and antielectron. Application of the HED mechanics gives the following process, which shows that the field structures of the photons (y) (Eqn 1.1) merge to form a transitional assembly O (Eqn 1.2), which disassembles into handed field structures (Eqn 1.3), which can be recognised as those of the electron and antielectron (Eqn 1.4):

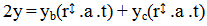(1.1)

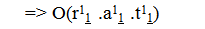(1.2)

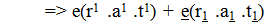(1.3)

(1.4)

This is because previous work [24] identifies that two photons corresponds to a discrete force structure represented by (r¹₁ .a¹₁ .t¹₁), hence the O transitional assembly (E1.2). This assembly is driven by the synchronous interaction [19] to partition into more stable HED structures (E1.3). These structures, by inspection, are the electron and antielectron. Thus it is relatively simple to use HED notation to represent the overall remanufacturing process of pair production. The minimum energy conditions for the input photons are therefore the rest masses of the electron and antielectron. The HED mechanics are for this NLHV design what Feynman diagrams are to QM, and the representations are not incompatible, though they have different levels of detail.

5. Discussion

5.1. Outcomes

This paper makes the novel contribution of providing a conceptual theory for how the evanescent field structures of the photon may be reassembled into an electron and antielectron. This has otherwise not been achieved with any of the other theories of physics, neither quantum mechanics, string/M-theory or classical electro-magnetic wave theory. Pair production represents one of the two process-directions in mass-energy equivalence, so provision of a natural explanation is an important conceptual development in foundational physics.

Another contribution is that this theory for pair production is logically consistent with a wider conceptual development for a new physics at the next deeper level below quantum mechanics and general relativity. This theory now has a logically consistent set of explanations for pair production (this paper), beta decay processes [24], the internal structure of the neutrino [ibid], annihilation processes [23], synchronous interaction (strong force) [19], internal structure of the nucleus atomic nuclides including all the nuclides from hydrogen to neon [20], time dilation [21], and asymmetrical baryogenesis [28]. In totality this demonstrates that the idea of discrete fields, coupled with a hidden variable structure, reinvigorates the hidden sector that has otherwise been quiescent for decades.

It provides novel insights into processes at the next deeper level of physics, and shows a candidate route to a new physics that spans particles, time, and gravitation. According to this perspective quantum mechanics is not wrong, but is simply a stochastic approximation to a deeper determinism at the hidden-variable level. Quantum mechanics is a coarse level of abstraction which approximates the two ended Cordus particule by a zero-dimensional point, with physical attributes such as spin being represented by mathematical ‘intrinsic variables’. In a similar manner general relativity (GR) and gravitation are not wrong, but instead the Cordus theory shows that they can be understood as higher-level abstractions of discrete field phenomena. Thus time is a dimension in general relativity, whereas the Cordus theory shows that time can be understood as an emergent property of matter that is mediated via the discrete fields [21], and only appears to be a dimension of space-time at a coarse level of scrutiny. The arrow (one-way direction) of time and the origins of entropy are also explained by the Cordus theory, whereas these are difficult problems for both QM and GR.

5.2. Implications and Interpretations

Polarisation dependency

There are several parts of this theory that are noteworthy. First, note that this theory requires two photons (not one) for the production of an electron-antielectron pair, and predicts that they need to be in complementary phases, i.e. opposite polarisation. The higher the energy the shorter the energisation cycles (higher frequency) and the more important it is for the photons to be pre-supplied in a state amenable to pair-production, hence opposite polarisation. This is a specific prediction, and afterwards we have found that it is consistent with the observational reality, though that was not known at the outset of this development. The effect has a conventional explanation in terms of angular momentum, so we cannot claim it as a unique prediction of our theory. Nonetheless it can be stated that the theory proposed here does recover the dependency of opposite polarisation, and can explain why it is more pronounced at higher energies.

Prediction of Real vs. Not-Real species differentiation

Note that we assumed that the outward discrete forces take the dexter hand, not sinister, at 4.2. We did this to avoid the formation of a peculiar configuration of discrete fields at step 5.2. This structure is not the usual matter-antimatter species differentiation but rather a solid-hole species type. These are the field configurations of (r₁ .a₁ .t₁) and 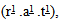which we term the positive notElectron !e(r₁ .a₁ .t₁) and negative antiNotElectron 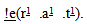We term these substances Not-Real matter. The selection of the Real as opposed to Not-Real production path may be justified by noting that under this theory the fabric of the universe, which comprises the discrete forces of all the particules in the accessible universe [25], is dominated by matter [28]. Hence dexter-handed discrete forces prevail in the fabric of the environment, so it is natural that the pair-production process should be compliant therewith. This also means that the Cordus theory proposes another form of inversion to the existing two of negative-positive charge, and matter-antimatter hand [22], this time an orthogonal Real vs. Not-Real species differentiation.

Recovery of electron holes

The theory provides an explanation for electron holes. The Not-Real matter is peculiar but not fundamentally problematic. Instead it is interpreted as holes in a sea of coherent electrons (for !e) or antielectrons If one electron is missing in a network of electrons, e.g. in a superconductor or local region of coherent electrons, then the fields inside that hole correspond to the fields of the neighbouring electrons, but reversed in direction. The hand of those fields is therefore unchanged. So according to the Cordus theory, this hole is not antimatter but an absence of matter, and behaves like a particule in its ability to move around. In other words these are empty locations where there are no reactive ends, but instead the discrete forces of the surrounding particules protrude into the hole. Consequently the hole does have an electric field structure and can interact accordingly, though its life is bound up with the fluid of particules around it. In this way the conduction of current by holes is recovered by the Cordus theory. These holes have been physically observed, so that part is not contentious. The novel contribution is providing physical explanations for these structures.

Pair-production and annihilation are complementary processes

Note that the output electron and antielectron particules could bond to form parapositronium and then annihilate back to photons (stage 5.3). Annihilation too is described in this theory: see [23] for the corresponding Cordus theory for para- and ortho-positronium annihilation processes. To avoid annihilation, the pair products must be parted before they form such bonds. We have not worked out the parting mechanism in detail. Our current concept is that an elastic recoil (see below) and separation of the two particules occurs, due to the way the span varies dynamically with frequency cycle (5.4). However this is tentative.

Other routes to pair-production

This pair-production process has been developed for the case of a collision between two photons. Another common situation in which pair-production occurs is the collision of a photon beam with say an electron. We suggest this can be accommodated within the theory by assuming the electron absorbs and then re-emits the photon. There are then multiple routes to pair production: either (a) the electron emits two photons, (b) a single photon is emitted and collides with another photon in the incoming beam, or (c) the energy emitted by the electron progresses directly into the emission of the discrete field structures of another electron and an antielectron, without passing through the photon stage. Variants of these have been identified [29]. In this three-fermion process the original electron experiences a recoil, which either (b) or (c) could explain. However of more interest is the nature of the recoil, which is dealt with next.

Direction of recoil

The theory explains the direction of recoil. Others have shown that the orientation of recoil depends on the polarisation of the incoming photons, and does not depend on the photon energy [29]. Such results are difficult to interpret using QM, for which polarisation is merely an intrinsic variable without physical embodiment. However the Cordus theory readily allows an appreciation of the issues, since the span of the particule is an important orientation variable. Thus the Cordus theory interprets both photon polarisation and electron spin as orientation of the main fibril of the respective particule. It is therefore natural to expect that the relative orientation of the photon and the target electron will determine the outcomes. In a similar way the Cordus theory has also explained basic optical polarisation effects such as Brewster’s angle [18], though in those cases it is the relative orientation of the photon and the optical plane that is important (the optical plane is interpreted as an aggregate of the orientations of multiple electrons in the substrate). Furthermore, the Cordus theory for photon emission makes the interesting prediction that the photon is emitted in a direction orthogonal to the electron span [27]. Thus, it is understandable that the orientation of the photon, hence polarisation, will affect the recoil of the host electron. The Cordus theory therefore accommodates and conceptually explains why the recoil should be dependent on and transverse to the incoming photons [30]. This is consistent with the observation that ‘the azimuthal distribution of the recoil electron is highly sensitive to the polarization of the incoming gamma radiation’ [29], and also consistent with the theoretical indications of polarisation-dependency [31]. Similar highly anisotropic recoil behaviour is also empirically evident in collisions occurring within an aligned molecular framework [30]. The dependency is so strong that it may be used in the inverse direction, as a measurement of photon polarisation [32]. Our comment in this regard is that the mathematical models predict the effect, and it is empirically observed. Yet an interpretation is difficult to make from within the 0-D point paradigm, whereas this is much easier from the NLHV solution provided by the Cordus theory. Likewise known other minor effects, like heavier atoms being more prone to pair production, can also be more easily explained when particles are acknowledged to have physical size, as here [20].

So the theory presented here provides a number of clear and unique theoretical predictions, and identifies the implications for experiments in an unambiguous way.

5.3. Limitations and Future Research

The theory is limited in being primarily conceptual. It does not provide the level of quantitative formulation for pair production as given by quantum field theory. Consequently some have criticised the present theory and laid a heavy burden to (a) show how the theory quantitatively reproduces empirical results, (b) explain how it reduces to a QFT, (c) show what problem it solves that is otherwise not explained by a QFT, and (d) provide testable and falsifiable predictions. However this is an unreasonable expectation given the early state of this theory and the limited number of people working on it compared to the vast resources of labour that have been spent on QFTs over an extended period of about a century. The present purpose was therefore not to attempt an irrefutable overthrow of QFT, but rather the more modest but nonetheless challenging objective of seeking to explain pair-production from the non-local hidden-variable (NLHV) sector. The theory is therefore still in the conceptual stage and does not yet have a mathematical formalism beyond its HED mechanics, nor it is able to provide numerically modelling of results. For example, the theory qualitatively describes the pair production process at the level of discrete fields, which is one channel of mass-energy equivalence, but does not quantify the relationship. These developments are left for future research as the concept matures.

There are also several streams of potential future work on the conceptual front. We have only considered electron-antielectron pair production, and there are other outcomes to consider, including the landscape of pions, kaons, etc.

Another research opportunity is to analyse asymmetrical genesis with this theory. This has been done and the results offer a solution to this problem too, a solution that is profoundly different to all other solutions and yet simple at its root [28].

6. Conclusions

A conceptual theory has been created within the NLHV framework of the Cordus theory, for the processes of electron-antielectron pair-production. The explanation is given in terms of the remanufacture of the discrete fields of the photon into those of the electron and antielectron, and the corresponding emergence of the inner structure of those particules. This is a significant outcome in that it provides an ontological explanation for mass-energy equivalence. The present paper has anticipated what the pair-production processes could look like in a NLHV solution, and annihilation, which is the inverse process, has also been demonstrated within this same framework. Thus the processes in both directions of mass-energy conversion have been explained. By comparison, quantum mechanics is unable to give an ontologically sufficient explanation for either of these processes. Consequently it is also significant is that the explanation comes from the NLHV sector. This has otherwise not historically been a productive area in which to seek solutions. The hidden-variable sector is shown to have yielded an alternative theory of fundamental physics with excellent explanatory power under physical realism. It provides novel insights into processes at the next deeper level of physics, and shows a candidate route to a new physics that spans particles, time, and gravitation.

Conflict of Interest Statement

The authors declare that there are no conflicts of interest regarding the publication of this article. The research was conducted without personal financial benefit from any third party funding body, nor did any such body influence the execution of the work.