-
Paper Information
- Paper Submission
-
Journal Information
- About This Journal
- Editorial Board
- Current Issue
- Archive
- Author Guidelines
- Contact Us
Journal of Nuclear and Particle Physics
p-ISSN: 2167-6895 e-ISSN: 2167-6909
2015; 5(1): 15-20
doi:10.5923/j.jnpp.20150501.03
EOS of Neutron Matter and Neutron Star Properties
Kh. S. A. Hassaneen1, 2, H. M. Abou-Elsebaa1, E. A. Sultan1, N. N. Abd Allah1
1Physics department, Faculty of Science, Sohag University, Sohag, Egypt
2Physics department, Faculty of Science, Taif University, Taif, Saudi Arabia
Correspondence to: H. M. Abou-Elsebaa, Physics department, Faculty of Science, Sohag University, Sohag, Egypt.
| Email: |  |
Copyright © 2015 Scientific & Academic Publishing. All Rights Reserved.
The Equation of State (EOS) of pure neutron matter at zero temperature is calculated up to five saturation densities within the Brueckner theory with the inclusion of three-body forces. Three different realistic and accurate two-body forces are considered to evaluate the G-matrix effective interaction for nuclear matter. These models are the chiral N3LO, the CD-Bonn and the Argonne V18, which give quite different EOS. Two types of three-body forces are included to the effective interaction, which might be important at densities several times that of nuclear matter density. Using a microscopic EOS for pure neutron matter, static properties of non-rotating neutron stars such as masses and radii are evaluated. The resulting maximum masses of neutron star using different interactions near 2 Mʘ are found to be in reasonable agreement with the measured ones PSR J1614−2230 (with Mmax = 1.97 ± 0.04 Mʘ) and PSR J0348+0432 (with Mmax = 2.01 ± 0.04 Mʘ).
Keywords: Contact term, Neutron star properties, Pure neutron matter, Three-body force
Cite this paper: Kh. S. A. Hassaneen, H. M. Abou-Elsebaa, E. A. Sultan, N. N. Abd Allah, EOS of Neutron Matter and Neutron Star Properties, Journal of Nuclear and Particle Physics, Vol. 5 No. 1, 2015, pp. 15-20. doi: 10.5923/j.jnpp.20150501.03.
Article Outline
1. Introduction
- The equation of state (EOS) for neutron star matter and infinite nuclear matter has been intensively studied for many years (see, for examples, Refs [1-5]). A correct description of the EOS would have far reaching consequences for topics ranging from the cooling of neutron stars [1, 2] to the heavy ion collisions physics [3]. Furthermore, experiments of radioactive ion beam [4, 5] have provided new information on the structure of unstable nuclei far from equilibrium. The latter may open the possibility of extracting information on the EOS for asymmetric matter and the density dependence of the nuclear symmetry energy. In the present work we do not discuss heavy-ion collisions.Moreover, Neutron stars are macroscopic objects where the stability is guaranteed by the Pauli principle of nucleons (together with a repulsive short-range interaction). Therefore the structure of a neutron star is dictated by the strong interaction (and, of course, gravity). The key ingredient that enters the stability condition is precisely the equation of state [6]. Recently, high-quality observational data of neutron stars set new stringent constraints for the EOS of cold and dense matter, otherwise inaccessible by experiment. The masses of two heavy pulsars have been determined with high precision. One of those is the radio pulsar (PSR) J1614−2230 with a mass M = (1.97 ± 0.04) Mʘ [7] and the other PSR J0348+0432 accurately determined mass with M = (2.01 ± 0.04) Mʘ [8], where Mʘ denotes the mass of the sun. Only a sufficiently stiff EOS can support such neutron stars against gravitational collapse. Whereas neutron star radii are much less accurately known, the combination of available data makes these objects nonetheless an indispensable tool to constrain possible EOS [9].Tews et al. [10] have done perturbation-theory calculations for pure neutron matter (PNM) with nuclear interactions derived from chiral perturbation theory including the full next-to-next-to-next-to-leading order (N3LO) contribution, with three- and four-body forces. Compared to calculations with three-body interactions defined only to next to- next-to-leading order (NNLO), the inclusion of all N3LO diagrams was found to be very important for nuclear structure and reactions. Their results provide constraints for the nuclear equation of state and for neutron-rich matter in astrophysics. While, in the present work, the N3LO NN potential complemented by phenomenological Urbana TBFs [11], instead of chiral three-nucleon forces, have been applied in calculations to neutron matter. In this work we will derive the EOS of PNM by many-body theory, derived from different realistic nucleon-nucleon (NN) interactions such as the CD-Bonn potential [12], the N3LO potential [13] and the Argonne V18 potential [14]. The many-body approaches that are used, the Brueckner-Hartree-Fock (BHF) approach with the inclusion of three-body force [11] or contact-term interaction to give more repulsive EOS [15].The plan of the paper is the following. The main features of BHF approach used in this work including two types of three-body forces are shown in the following section. The results for the neutron matter equation of state are presented and discussed in Sec. 3. In Sec. 4 neutron star matter is examined and discussed in view of the new observational constraints. Finally, the conclusions and perspectives for the present work are given in Sec. 5.
2. BHF Approach
- One main feature of the BHF approach to nuclear matter is that the binding energy and related quantities such as the self-energy, i.e. mass operator, can be developed according to the so-called hole-line expansion. Its expression is
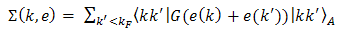 | (1) |
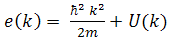 | (2) |
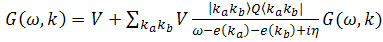 | (3) |
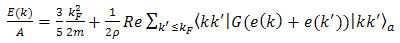 | (4) |
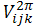 due to two-pion exchange with the excitation of an intermediate Δ-resonance, and a repulsive phenomenological term
due to two-pion exchange with the excitation of an intermediate Δ-resonance, and a repulsive phenomenological term 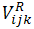
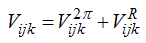 | (5) |
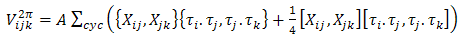 | (6) |
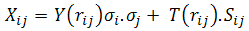 | (7) |

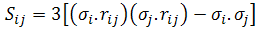 is called the tensor operator. Both Y(r) and T(r) are the Yukawa and tensor functions associated to the one-pion exchange as in the two-body potential. The repulsive term is written as
is called the tensor operator. Both Y(r) and T(r) are the Yukawa and tensor functions associated to the one-pion exchange as in the two-body potential. The repulsive term is written as 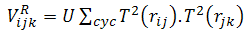 | (8) |
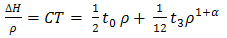 | (9) |
|
3. EOS for Pure Neutron Matter
- The energy per nucleon of neutron matter is the only input required for determining the mass-radius relationship for neutron stars, and hence the ranges of physically allowable neutron star masses. In Figure 1. we show the results for the energy per nucleon in the case of a system composed of neutrons only. For three choices of the NN potential, curves of EOS with two types TBF are displayed supplemented to BHF approach. When phenomenological TBF are used, the parameters A and U are fixed by the calculation of saturation properties in the symmetric case.
4. Neutron Star Structure
- The structure of a neutron star is characterized by its mass and radius. Additional parameters of interest are the moment of inertia and the crust thickness; these are important for the dynamics and transport properties of pulsars. In the present work, we assume that a neutron star is a spherically symmetric distribution of mass in hydrostatic equilibrium. The effects of rotations can be neglected; assume there is no magnetic field. Then the equilibrium configurations are simply obtained by solving the Tolman – Oppenheimer - Volkoff (TOV) equations [21, 22]:
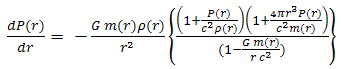 | (10) |
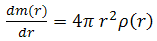 | (11) |
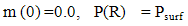 | (12) |
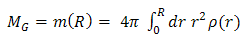 | (13) |
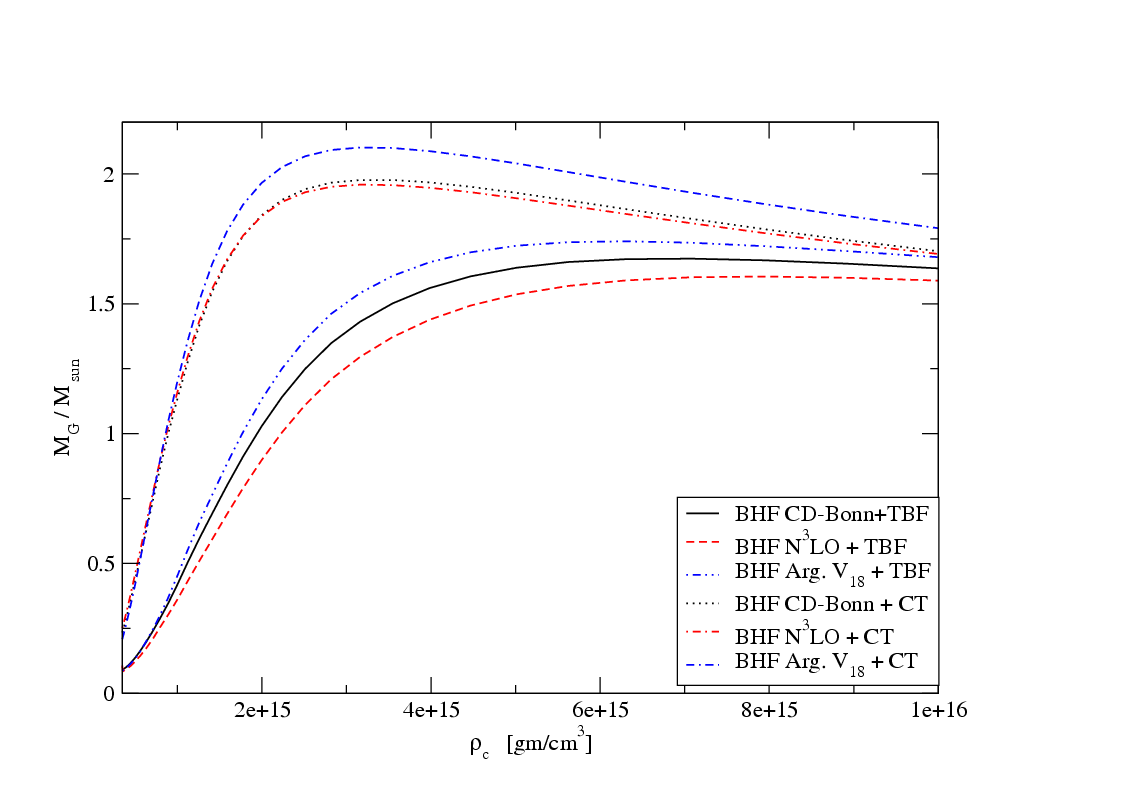 | Figure 3. Neutron star gravitational masses MG (in units of Mʘ) as a function of the central density ρc in units of gm/cm3 for different potentials. The notations are the same as Figure 2 |

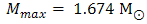 at a central density ρc/ ρ0=25 with a radius R = 6.611 km for CD-Bonn + TBF model. Also we find a maximum mass of neutron star
at a central density ρc/ ρ0=25 with a radius R = 6.611 km for CD-Bonn + TBF model. Also we find a maximum mass of neutron star
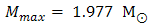 at a central density ρc/ ρ0=11 with a radius R = 9.469 km for CD-Bonn + CT model. In the case of N3LO+ TBF, one notes that a maximum mass of
at a central density ρc/ ρ0=11 with a radius R = 9.469 km for CD-Bonn + CT model. In the case of N3LO+ TBF, one notes that a maximum mass of
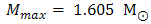 at a central density ρc/ ρ0 = 28 with a radius R = 6.271 km. If we use N3LO+ CT, we find a maximum mass of
at a central density ρc/ ρ0 = 28 with a radius R = 6.271 km. If we use N3LO+ CT, we find a maximum mass of
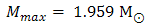 at a central density ρc/ ρ0=11 with a radius R = 9.559 km. In the case of Argonne V18 + TBF, we find a maximum mass of neutron star
at a central density ρc/ ρ0=11 with a radius R = 9.559 km. In the case of Argonne V18 + TBF, we find a maximum mass of neutron star
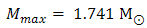 at a central density ρc/ ρ0=22.5 with a radius R = 6.908 km. Lastly, in the case of Argonne V18 + CT a maximum mass of neutron star has the value
at a central density ρc/ ρ0=22.5 with a radius R = 6.908 km. Lastly, in the case of Argonne V18 + CT a maximum mass of neutron star has the value
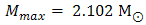 at a central density ρc/ ρ0=11 with a radius R = 9.481 km.Finally one can see from the two figures (2 and 3) that neutron stars properties calculated with a stiff equation of state (e.g., CD-Bonn + CT, N3LO + CT and Argonne V18+ CT) have greater maximum masses than neutron stars derived from a soft equation of state. Furthermore neutron stars derived from a stiff equation of state have a lower central density and larger radius than do neutron stars of the same mass computed from a soft equation of state. The present results are more compatible with recent microscopic calculations of neutron matter based on nuclear interactions derived from chiral effective field theory [26]. They have constructed three representative EOSs (soft, intermediate, and stiff), consistent with the constraints from nuclear physics and observation. To one obtain more repulsive EOS, one can go beyond the present approach [27].
at a central density ρc/ ρ0=11 with a radius R = 9.481 km.Finally one can see from the two figures (2 and 3) that neutron stars properties calculated with a stiff equation of state (e.g., CD-Bonn + CT, N3LO + CT and Argonne V18+ CT) have greater maximum masses than neutron stars derived from a soft equation of state. Furthermore neutron stars derived from a stiff equation of state have a lower central density and larger radius than do neutron stars of the same mass computed from a soft equation of state. The present results are more compatible with recent microscopic calculations of neutron matter based on nuclear interactions derived from chiral effective field theory [26]. They have constructed three representative EOSs (soft, intermediate, and stiff), consistent with the constraints from nuclear physics and observation. To one obtain more repulsive EOS, one can go beyond the present approach [27].5. Conclusions
- We studied neutron star properties, in particular NS’s maximum masses and radius using the BHF approximation with exact Pauli’s operator with the inclusion of two types of three body forces. The three body forces that are used, the phenomenological TBF and a simple contact term added to the effective interaction. It is found that neutron star properties are sensitive to microscopic model calculations, this means that the maximum masses and radii depend on the stiffness of the suggested EOS. Neutron star properties calculated with a stiff EOS have a lower central density, a larger radius than stars of the same mass computed from a soft EOS. In general, simple construction of neutron stars from the EOS of pure neutron matter is not enough for a consistency check between the theoretical neutron star maximum mass and the observed neutron star masses. If it is possible to duly deduce the information on the EOS of nuclear matter by ignoring other constituents than nucleons, it would be reasonable to focus on low mass neutron stars (see, e.g., Sotani et al. [28]).
References
| [1] | C.J. Pethick and D.G. Ravenhall, Annu. Rev. Nucl. Part. Phys. 45, 429, (1995). |
| [2] | M. Prakash, Phys. Rep. 242, 191, (1994). |
| [3] | B.-A. Li, C.M. Ko and Z. Ren, Physical Review Letter 78, 1644, (1997). |
| [4] | T. Klähn et al., “Constraints on the high-density nuclear equation of state from the phenomenology of compact stars and heavy-ion collisions, Physical Review C 74, 035802 (2006). |
| [5] | Z. Kohley et al., "Exploiting Neutron-Rich Radioactive Ion Beams to Constrain the Symmetry Energy." Physical Review C 88, 041604 (2013). |
| [6] | S. Leupold, K. Redlich, M. Stephanov, A. Andronic, D. Blaschke, et al., “Part I Bulk Properties of Strongly Interacting Matter”, Lect. Notes Phys. 814, 39–334 (2011), DOI 10.1007/978-3-642-13293-3_3 |
| [7] | P.B. Demorest, T. Pennucci, S.M. Ransom, M.S.E. Roberts, and J.W.T. Hessels, Nature 467, 1081 (2010). |
| [8] | J. Antoniadis , P. C. Freire, N. Wex, T. M. Tauris, R. S. Lynch, M. H. van Kerkwijk, M. Kramer, C. Bassa, V. S. Dhillon, T. Driebe et al., Science 340, 6131 (2013). |
| [9] | T. Hell and W. Weise, Physical Review C 90, 045801 (2014). |
| [10] | I. Tews, T. Krüger, K. Hebeler, and A. Schwenck. Physical Review Letter, 110, 032504, (2013). |
| [11] | M. Baldo and Alaa Eldeen Shaban, Phys. Lett. B 661, 373 (2008). |
| [12] | R. Machleidt, Physical Review C 63: 024001, (2001). |
| [13] | D. R. Entem and R. Machleidt, Physical Review C 68, 041001 (2003). |
| [14] | R. B. Wiringa, V. G. J. Stoks, and R. Schiavilla, Physical Review C 51, 38 (1995). |
| [15] | Khaled Hassaneen and Hesham Mansour, “The Hot and Cold Properties of Nuclear Matter”, J. Nuc. Part. Phys. 3(4): 77-96, (2013); DOI: 10.5923/j.jnpp.20130304.05 |
| [16] | J. P. Jeukenne, A. Lejeune, and C. Mahaux, Phys. Rep. 25, 83 (1976). |
| [17] | E. Schiller, H. Müther and P.Czerski, Physical Review C 59, 2934 (1999). |
| [18] | A. Lejeune, P. Grange, M. Martzolff and J. Cugnon , Nucl. Phys. A 453, 189 (1986). |
| [19] | P. Gögelein, E.N.E. van Dalen, Kh. Gad, Kh.S.A. Hassaneen, and, Phys Physical Review C 79, 024308 (2009). |
| [20] | M. Kohno, Physical Review C 88, 064005 (2013). |
| [21] | J. R. Oppenheimer and G. M. Volkoff, Phys. Rev. 55, 374 (1939). |
| [22] | R.C. Tolman, Proc. Nat. Acad. Sci. USA 20, 3 (1934). |
| [23] | G. Taranto, M. Baldo and G.F. Burgio, Physical Review C 87, 045803 (2013). |
| [24] | G. Baym, C. Pethick, and D. Sutherland, ApJ 170, 299 (1971). |
| [25] | C. P. Lorenz, D. G. Ravenhall and C. J. Pethick, Physical Review Letter 70, 379 (1993). |
| [26] | K. Hebeler, J.M. Lattimer, C.J. Pethick, and A. Schwenk, The Astrophys. J. 773:11, (14pp), (2013). |
| [27] | K. Hassaneen, “the Equation of State of Nuclear Matter and Neutron Stars Properties”. Journal of Modern Physics, 5, 1713-1724 (2014). doi: 10.4236/jmp.2014.516171. |
| [28] | H. Sotani, K. Iida, K. Oyamatsu, and A. Ohnishi, Prog. Theor. Exp. Phys., 051E01 (2014). |
 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML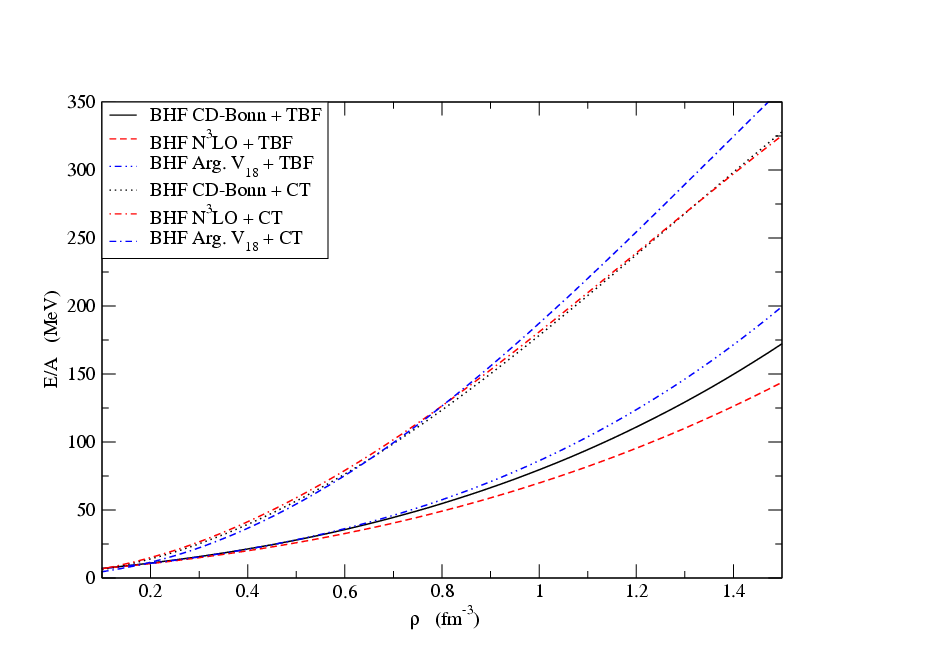
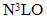 + TBF (short dashed line),
+ TBF (short dashed line), 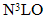 + CT (dot-dashed line), the Argonne V18 potential + TBF (double dot-dashed line) and Argonne V18 potential + CT (double dashed dot line)
+ CT (dot-dashed line), the Argonne V18 potential + TBF (double dot-dashed line) and Argonne V18 potential + CT (double dashed dot line)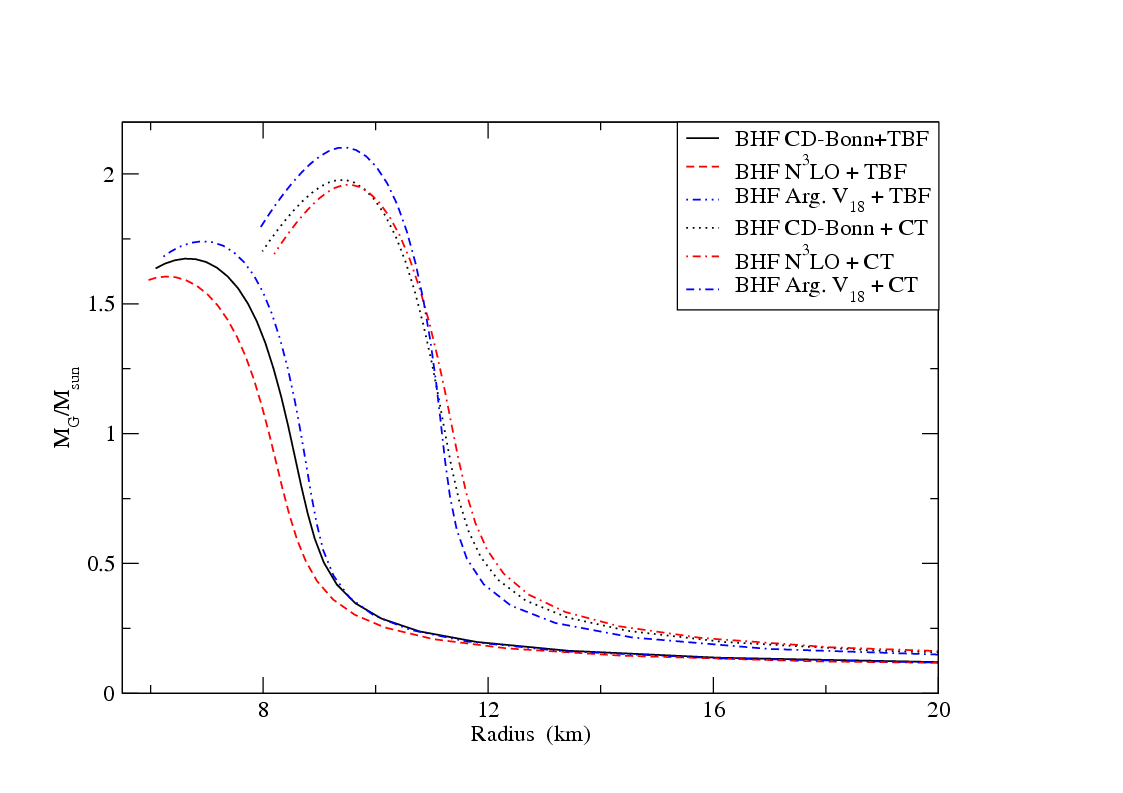
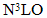 + TBF (short dashed line),
+ TBF (short dashed line), 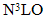 + CT (dot-dashed line), the Argonne V18 potential + TBF (double dot-dashed line) and Argonne V18 potential + CT (double dashed dot line)
+ CT (dot-dashed line), the Argonne V18 potential + TBF (double dot-dashed line) and Argonne V18 potential + CT (double dashed dot line)