| [1] | I. Bombaci, U. Lombardo, Phys. Rev. C 44, 1892 (1991). |
| [2] | W. Zuo, I. Bombaci, U. Lombardo, Phys. Rev. C 60,024605 (1999). |
| [3] | W. Zuo, A. Lejeune, U. Lombardo, J.F. Mathiot, Eur.Phys. J. A 14, 469 (2002). |
| [4] | W. Zuo, L.G. Cao, B.A. Li, U. Lombardo, C.W. Shen, Phys. Rev. C 72, 014005 (2005). |
| [5] | W. Zuo, U. Lombardo, H.J. Schulze, Z.H. Li, Phys. Rev.C 74, 014317 (2006). |
| [6] | I. Vida˜na, C. Providˆencia, A. Polls, A. Rios, Phys. Rev.C 80, 045806 (2009). |
| [7] | I. Vida˜na, A. Polls, C. Providˆencia, Phys. Rev. C 84,062801 (2011). |
| [8] | H. Huber, F. Weber, M.K. Wiegel, Phys. Rev. C 51, 1790 (1995). |
| [9] | C.H. Lee, T.T.S. Kuo, G.Q. Li, G.E. Brown, Phys. Rev.C 57, 3488 (1998). |
| [10] | E.N.E. van Dalen, C. Fuchs, A. Faessler, Nucl. Phys. A744, 227 (2004). |
| [11] | E.N.E. van Dalen, C. Fuchs, A. Faessler, Phys. Rev. C 72, 065803 (2005). |
| [12] | E.N.E. van Dalen, C. Fuchs, A. Faessler, Phys. Rev. Lett.95, 022302 (2005). |
| [13] | Z.Y. Ma, J. Rong, B.Q. Chen et al., Phys. Lett. B 604,170 (2004). |
| [14] | P. Krastev, F. Sammarruca, Phys. Rev. C 73, 014001 (2006). |
| [15] | T. Klahn, D. Blaschke, S. Typel et al., Phys. Rev. C 74,035802 (2006). |
| [16] | T. Frick, H. M¨uther, A. Rios, A. Polls, A. Ramos, Phys.Rev. C 71, 014313 (2005). |
| [17] | Kh. Gad, Kh. S.A. Hassaneen, Nucl. Phys. A 793, 67(2007). |
| [18] | A. Rios, A. Polls, W.H. Dickhoff, Phys. Rev. C 79, 064308(2009). |
| [19] | A. Rios, V. Soma, Phys. Rev. Lett. 108, 012501 (2012). |
| [20] | P. Bozek, P. Czerski, Eur. Phys. J. A 11, 271 (2001). |
| [21] | P. Bozek, Eur. Phys. J. A 15, 325 (2002). |
| [22] | P. Bozek, Phys. Rev. C 65, 054306 (2002). |
| [23] | V. Soma, P. Bozek, Phys. Rev. C 78, 054003 (2008). |
| [24] | V. Soma, P. Bozek, Phys. Rev. C 80, 025803 (2009). |
| [25] | Y. Dewulf, D. Van Neck, M. Waroquier, Phys. Lett. B510, 89 (2001). |
| [26] | Y. Dewulf, D. Van Neck, M. Waroquier, Phys. Rev. C 65,054316 (2002). |
| [27] | Y. Dewulf, W.H. Dickhoff, D. Van Neck, E.R. Stoddard, M. Waroquier, Phys. Rev. Lett. 90, 152501 (2003). |
| [28] | R.B. Wiringa, V. Fiks, A. Fabrocini, Phys. Rev. C 38,1010 (1988). |
| [29] | A. Akmal, V.R. Pandharipande, D.G. Ravenhall, Phys. Rev. C 58, 1804 (1998). |
| [30] | G.H. Bordbar, M. Modarres, Phys. Rev. C 57, 714 (1998). |
| [31] | M. Modarres, G.H. Bordbar, Phys. Rev. C 58, 2781(1998). |
| [32] | G.H. Bordbar, M. Bigdeli, Phys. Rev. C 75, 045804(2007). |
| [33] | G.H. Bordbar, M. Bigdeli, Phys. Rev. C 77, 015805(2008). |
| [34] | J. Carlson, V.R. Pandharipande, R.B. Wiringa, Nucl. Phys. A 401, 59 (1983). |
| [35] | P. Grang´e, A. Lejeune, M. Martzolff, J.F. Mathiot, Phys. Rev. C 40, 1040 (1989). |
| [36] | W. Zuo, A. Lejeune, U. Lombardo, J.F. Mathiot, Nucl. Phys. A 706, 418 (2002). |
| [37] | Z.H. Li, U. Lombardo, H.J. Schulze, W. Zuo, Phys. RevC 77, 034316 (2008). |
| [38] | Maclleidt R. Adv. Nucl. Phys., 19, 189(1989). |
| [39] | H.M.M. Mansour and A. Gamoudi, Physics of atomic nuclei 75,430(2012). |
| [40] | Machleidt R. Phys. Rev. C63 (2001), 024001. |
| [41] | Stoks V. G. J, Klomp R. A. M, Terheggen C. P. F and de Swart J. J, Phys. Rev. C49 (1994), 2950. |
| [42] | Wiringa R. B, Stoks V. G. J. and Schiavilla R, Phys. Rev C51 (1995), 38. |
| [43] | Hesham M.M. Mansour, Khaled S.A. Hassaneen, Journal of Nuclear and Particle Physics 2(2) (2012) 14. |
| [44] | Khaled Hassaneen and Hesham Mansour, Journal of modern physics 4(5B),37(2013). |
| [45] | Khaled Hassaneen and Hesham Mansour, Journal of Nuclear and Particle Physics 2013, 3(4): 77-96. |
| [46] | H. M. M. Mansour and Kh. S. A. Hassaneen, Physics of atomic nuclei, 2014, vol 77, No. 3, pp. 290–298. |
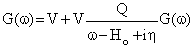
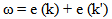
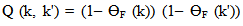
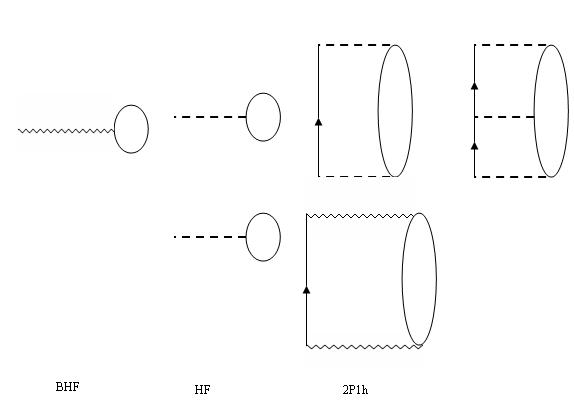
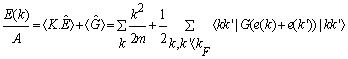
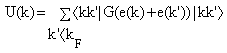
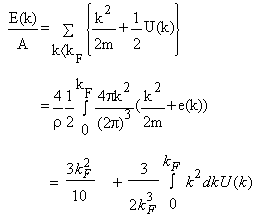
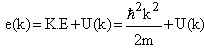
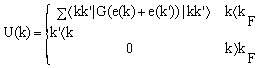
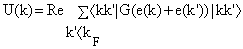
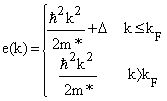
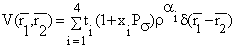
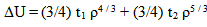
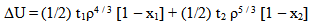
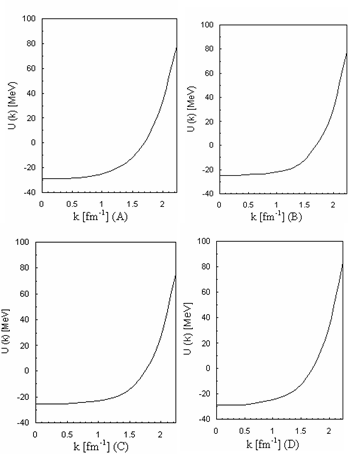
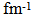 ) for continuous choice of different potentials
) for continuous choice of different potentials
 ) for continuous choice of different potentials
) for continuous choice of different potentials Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML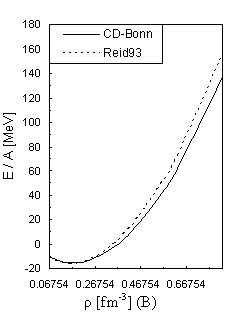
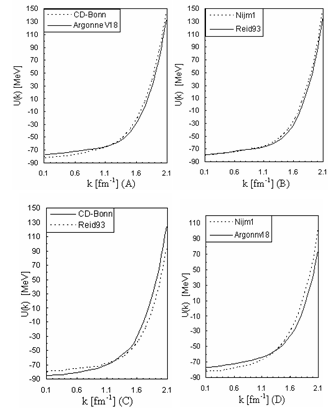
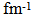 ) for different potentials (A and B) for conventional choice, (C and D) for continuous choice
) for different potentials (A and B) for conventional choice, (C and D) for continuous choice