-
Paper Information
- Next Paper
- Paper Submission
-
Journal Information
- About This Journal
- Editorial Board
- Current Issue
- Archive
- Author Guidelines
- Contact Us
Journal of Nuclear and Particle Physics
p-ISSN: 2167-6895 e-ISSN: 2167-6909
2014; 4(6): 164-170
doi:10.5923/j.jnpp.20140406.02
Elliptic Flow in Heavy Ion Collisions
Abhilasha Saini1, Sudhir Bhardwaj2
1Department of Physics, Gyan Vihar University, Jaipur, & Atharva college of Engg. Malad, Mumbai, India
2Govt. College of Engineering & Technology, Bikaner, India
Correspondence to: Abhilasha Saini, Department of Physics, Gyan Vihar University, Jaipur, & Atharva college of Engg. Malad, Mumbai, India.
| Email: |  |
Copyright © 2014 Scientific & Academic Publishing. All Rights Reserved.
The study of quark-gluon plasma state in high energy heavy ion collisions is quite complicated as the system is dynamical. But still some detectable signals are present with are very helpful to understand this high energy phenomena. The measurement of elliptic flow is one of those experimentally measured variables. One of the major experimental evidence for the existence of thermalized system is the large anisotropic flow of hadrons. The anisotropic flow is the anisotropy of the particle azimuthal distribution in the momentum space with respect to the reaction plane and supposed to be sensitive to the extent of thermalization of the system immediately after the collision. The various hadron yield with respect to the reaction plane is characterized by Fourier expansion as the thermalised system behave like ideal fluid and the elliptic flow is defined by the second Fourier coefficient 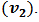 The theoretical calculations matches with the experimental observations well when the event by event fluctuations are considered for the measurement of flow and the Monte Carlo Glauber models are very much helpful to evaluate initial stage parameters.
The theoretical calculations matches with the experimental observations well when the event by event fluctuations are considered for the measurement of flow and the Monte Carlo Glauber models are very much helpful to evaluate initial stage parameters.
Keywords: Heavy ion collisions, Anisotropic flow, Monte carlo glauber models
Cite this paper: Abhilasha Saini, Sudhir Bhardwaj, Elliptic Flow in Heavy Ion Collisions, Journal of Nuclear and Particle Physics, Vol. 4 No. 6, 2014, pp. 164-170. doi: 10.5923/j.jnpp.20140406.02.
1. Introduction
- In relativistic heavy ion collisions a large amount of energy is dumped into a very small volume, when the two heavy nuclei collide, and the observation of these collisions at Alternating gradient synchrotron (AGS) at BNL and the super proton synchrotron at CERN have been recorded for different energy ranges and from light to heavy nuclei. These collisions are pictured with various stages in between the initial stage and the end point, with particles observed in the detectors around the collision points, and many detectable signals and experimental observables are recorded at these stages. When the Lorentz contracted nuclei pass through each other, the vacuum left behind is filled with a colour field, indicates the attraction of the two nuclei and the energy of the colour field leads to the production of matter and anti-matter.The impact parameter roughly defines the nuclei participating in a collision
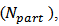 the number of binary collisions occurring
the number of binary collisions occurring 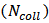 and about the distribution of initial energy density in the collision region. The small impact parameter collisions are defined as the central collisions and the collisions with large value of impact parameter are called peripheral collisions.With the other detectable signals of the initial stage of heavy ion collisions one of the important signal is the elliptic-flow. After the initial binary collisions the interacting system reaches to a local thermal equilibrium, and the pressure gradients arise. The pressure gradients are steeper along the direction of impact parameter and lead to anisotropic momentum distribution of particles which is defined as elliptic flow. The yield of various hadrons with respect to the reaction plane can be characterized by Fourier expansion, where the different coefficients measure different anisotropies present in the system. The first coefficient is known as the directed flow
and about the distribution of initial energy density in the collision region. The small impact parameter collisions are defined as the central collisions and the collisions with large value of impact parameter are called peripheral collisions.With the other detectable signals of the initial stage of heavy ion collisions one of the important signal is the elliptic-flow. After the initial binary collisions the interacting system reaches to a local thermal equilibrium, and the pressure gradients arise. The pressure gradients are steeper along the direction of impact parameter and lead to anisotropic momentum distribution of particles which is defined as elliptic flow. The yield of various hadrons with respect to the reaction plane can be characterized by Fourier expansion, where the different coefficients measure different anisotropies present in the system. The first coefficient is known as the directed flow 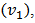 and the second one is defined as elliptic flow
and the second one is defined as elliptic flow 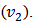 Further the partonic matter of system is converted into hadrons as the collision medium expands and cools down. These hadrons initially go through inelastic collisions. As the system keeps cooling down further, below a certain temperature inelastic collisions between hadrons stop and in this state different particle yields is completely defined. This stage is called Chemical freeze-out. Further expansion and cooling of system leads to the elastic collisions of hadrons, and a situation comes, when the produced particle stop colliding called Kinetic freeze-out.At different stages of heavy ion collision it is possible to probe the hot and dense medium via different measurable signals. Here in this paper we shall concentrate only on elliptic flow. Quantitatively the elliptic flow is indicated by the second Fourier coefficient
Further the partonic matter of system is converted into hadrons as the collision medium expands and cools down. These hadrons initially go through inelastic collisions. As the system keeps cooling down further, below a certain temperature inelastic collisions between hadrons stop and in this state different particle yields is completely defined. This stage is called Chemical freeze-out. Further expansion and cooling of system leads to the elastic collisions of hadrons, and a situation comes, when the produced particle stop colliding called Kinetic freeze-out.At different stages of heavy ion collision it is possible to probe the hot and dense medium via different measurable signals. Here in this paper we shall concentrate only on elliptic flow. Quantitatively the elliptic flow is indicated by the second Fourier coefficient 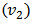 of the azimuthal particle distribution relative to the reaction plane (defined by the impact parameter and the beam axis.). The relativistic hydrodynamical models are able to explain and picture the expansion of hot and dense thermalized system very well at low viscosity [1]. The dynamical properties of the system resemble to the liquid rather than a gas. The study of this matter at RHIC energies shows an interesting feature, by the study of azimuthal anisotropy of final state particles, for different particle species.The figure 1, shows the magnitude of elliptic flow for different particle species, and the figure 2 which indicates the quantities when scaled with the number of constituent quarks like
of the azimuthal particle distribution relative to the reaction plane (defined by the impact parameter and the beam axis.). The relativistic hydrodynamical models are able to explain and picture the expansion of hot and dense thermalized system very well at low viscosity [1]. The dynamical properties of the system resemble to the liquid rather than a gas. The study of this matter at RHIC energies shows an interesting feature, by the study of azimuthal anisotropy of final state particles, for different particle species.The figure 1, shows the magnitude of elliptic flow for different particle species, and the figure 2 which indicates the quantities when scaled with the number of constituent quarks like 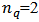 for mesons and
for mesons and 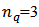 for (anti) baryons. At very low energies, the elliptic flow is positive and indicates the in plane momentum anisotropy because the spectator part exits collision region slowly and blocks the in-plane emission from the nuclear overlap zone and the particles emitted from the participant region are bounced out of plane and thus a negative
for (anti) baryons. At very low energies, the elliptic flow is positive and indicates the in plane momentum anisotropy because the spectator part exits collision region slowly and blocks the in-plane emission from the nuclear overlap zone and the particles emitted from the participant region are bounced out of plane and thus a negative 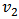 coefficient. With growing energy the spectators escape faster from the region and the bouncing off-plane dynamics is less dominating. Simultaneously at energies higher than
coefficient. With growing energy the spectators escape faster from the region and the bouncing off-plane dynamics is less dominating. Simultaneously at energies higher than 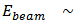 400 MeV/A, pressure gradients start to develop in-plane contribute positively to
400 MeV/A, pressure gradients start to develop in-plane contribute positively to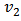 . These two things are competing with each other result into a monotonic grow of the elliptic flow coefficient with energy. At
. These two things are competing with each other result into a monotonic grow of the elliptic flow coefficient with energy. At 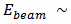 4 GeV/A,
4 GeV/A, 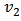 again becomes positive indicates that the pressure gradient developed in plane is dominated over other factors.
again becomes positive indicates that the pressure gradient developed in plane is dominated over other factors. | Figure 2. Left: The figure shows a plot, 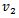 versus versus 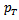 and transverse kinetic energy and transverse kinetic energy  Figure from [19] Figure from [19] |
 | Figure 3. A plot shows the plot of ratios  versus versus  and and 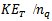 where where 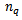 is the number of constituent quarks for each type of the particle species considered. Figure from [19] is the number of constituent quarks for each type of the particle species considered. Figure from [19] |
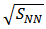 = 200 GeV, as a function of number of participating nucleons, the results can be seen in the figure 4.
= 200 GeV, as a function of number of participating nucleons, the results can be seen in the figure 4.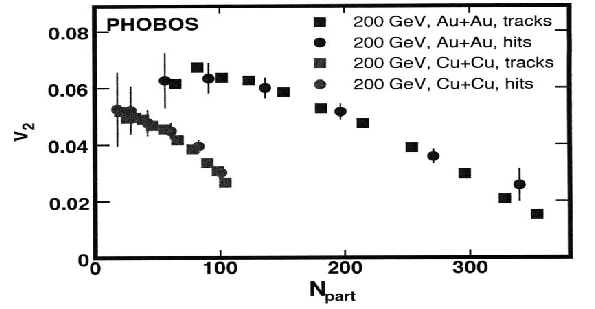 | Figure 4. Elliptic flow parameter as a function of number of participating nucleons in Au+Au (blue) and Cu+Cu (red) collisions at 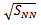 = 200 GeV [2] = 200 GeV [2] |
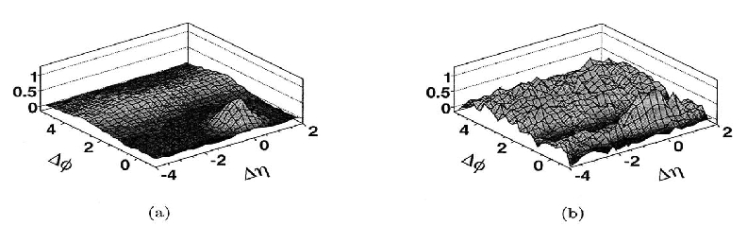 | Figure 5. Correlated yield as a function of for (a) PYTHIA p+p model and (b) 0-30% central Au+Au data at 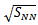 = 200 GeV with respect to a trigger particle with = 200 GeV with respect to a trigger particle with 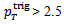 GeV/c [3] GeV/c [3] |
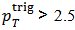 GeV/c in p+p collisions modeled by PYTHIA, and in most central Au+Au events (0-30%) at
GeV/c in p+p collisions modeled by PYTHIA, and in most central Au+Au events (0-30%) at 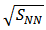 = 200 GeV, as a function of pseudo rapidity
= 200 GeV, as a function of pseudo rapidity 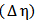 and azimuthal separations
and azimuthal separations 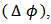 between particle pairs. When Au+Au collisions were compared with the p+p system a very rich correlation structure is observed in Au+Au collisions, also an excess yield of correlated particles at
between particle pairs. When Au+Au collisions were compared with the p+p system a very rich correlation structure is observed in Au+Au collisions, also an excess yield of correlated particles at 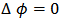 and
and 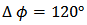 was found for
was found for 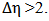 The structure defined as “ridge” or “broad away side” and studied experimentally [3-8] and different theoretical models were used for understanding of their origin [9-15]. But none of the models describe the experimental results successfully [16].Further the results of observed elliptic flow were supposed to be explained by the consideration of event by event fluctuations in the initial geometry [2]. The anisotropy of the initial geometry can be characterized by the eccentricity of the transverse shape of the initial nuclear overlap region [17].In Glauber model, even for the most central collisions, the eccentricity of the region is defined by the event by event distribution of the nucleon-nucleon interaction points, is finite and has a large effect of the event by event fluctuations on the elliptic flow. The fluctuations in the initial collision geometry may play a key role to find and understand the source of ridge and broad away side structures in particle correlation measurements.Eccentricity and the elliptic flow:Anisotropies in the distribution of particle momentum relative to the reaction plane, is defined as the anisotropic collective flow, in the heavy ion collisions. The azimuthal anisotropy in the particle production is characterized by the Fourier transformation with respect to the reaction plane angle
The structure defined as “ridge” or “broad away side” and studied experimentally [3-8] and different theoretical models were used for understanding of their origin [9-15]. But none of the models describe the experimental results successfully [16].Further the results of observed elliptic flow were supposed to be explained by the consideration of event by event fluctuations in the initial geometry [2]. The anisotropy of the initial geometry can be characterized by the eccentricity of the transverse shape of the initial nuclear overlap region [17].In Glauber model, even for the most central collisions, the eccentricity of the region is defined by the event by event distribution of the nucleon-nucleon interaction points, is finite and has a large effect of the event by event fluctuations on the elliptic flow. The fluctuations in the initial collision geometry may play a key role to find and understand the source of ridge and broad away side structures in particle correlation measurements.Eccentricity and the elliptic flow:Anisotropies in the distribution of particle momentum relative to the reaction plane, is defined as the anisotropic collective flow, in the heavy ion collisions. The azimuthal anisotropy in the particle production is characterized by the Fourier transformation with respect to the reaction plane angle 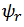 as-
as-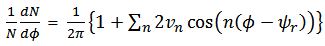 | (1) |
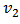 is defined as the elliptic flow which appears due to the anisotropy in the initial collision geometry.The eccentricity in general is quantified as the anisotropy of the collision geometry-
is defined as the elliptic flow which appears due to the anisotropy in the initial collision geometry.The eccentricity in general is quantified as the anisotropy of the collision geometry- | (2) |
 [23].On the basis of these observations, it is found that the elliptic flow can be understood well by the plot of elliptic flow scaled by eccentricity,
[23].On the basis of these observations, it is found that the elliptic flow can be understood well by the plot of elliptic flow scaled by eccentricity, 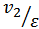 as a function of particle density in the transverse plane,
as a function of particle density in the transverse plane, 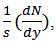 where the initial overlap area s and eccentricity
where the initial overlap area s and eccentricity 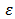 is taken from Glauber model calculations[26].The plot for elliptic flow results from AGS, SPS, and RHIC experiments are seen at different collision energies with different projectiles and different centralities lead to the conclusion that the heavy ion collisions satisfy the assumption of hydrodynamical calculations made in the initial state thermalization and interaction near zero mean free path limit (23, 27, 28).From the hydro-dynamical calculations, which implement finite mean free path, it is observed that the elliptic flow measurements are very sensitive to the viscosity of the system. A large uncertainty in the value of eccentricity is found when different approaches were used to quantify the initial geometry parameters.
is taken from Glauber model calculations[26].The plot for elliptic flow results from AGS, SPS, and RHIC experiments are seen at different collision energies with different projectiles and different centralities lead to the conclusion that the heavy ion collisions satisfy the assumption of hydrodynamical calculations made in the initial state thermalization and interaction near zero mean free path limit (23, 27, 28).From the hydro-dynamical calculations, which implement finite mean free path, it is observed that the elliptic flow measurements are very sensitive to the viscosity of the system. A large uncertainty in the value of eccentricity is found when different approaches were used to quantify the initial geometry parameters.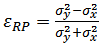 | (3) |
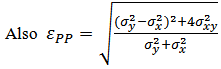 | (4) |
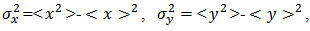 and
and 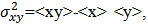 are the event-by-event (co-)variances of the participant nucleon distributions projected on the transverse axes, x and y, also RP refers to the reaction plane & PP refers to the participant plane. For the calculations in participant plane, the coordinate axes are tilted according to the ellipse formed in the collision region given in the Fig. 7.
are the event-by-event (co-)variances of the participant nucleon distributions projected on the transverse axes, x and y, also RP refers to the reaction plane & PP refers to the participant plane. For the calculations in participant plane, the coordinate axes are tilted according to the ellipse formed in the collision region given in the Fig. 7.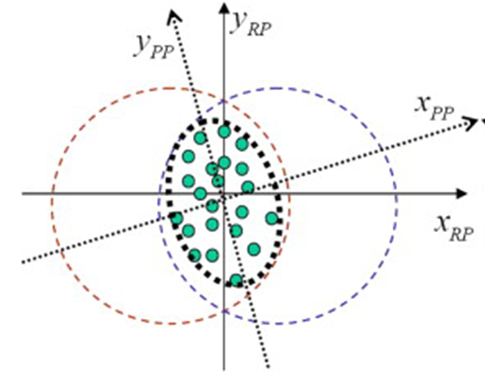 | Figure 7. The reaction plane and participant plane in the collision region |
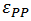 is calculated considering the distribution of nucleons inside the nuclei.
is calculated considering the distribution of nucleons inside the nuclei.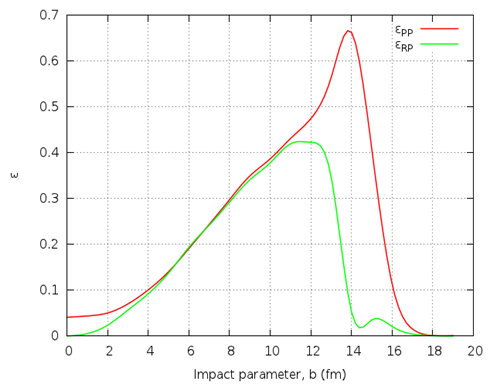 | Figure 8. Plot of eccentricity with impact parameter |
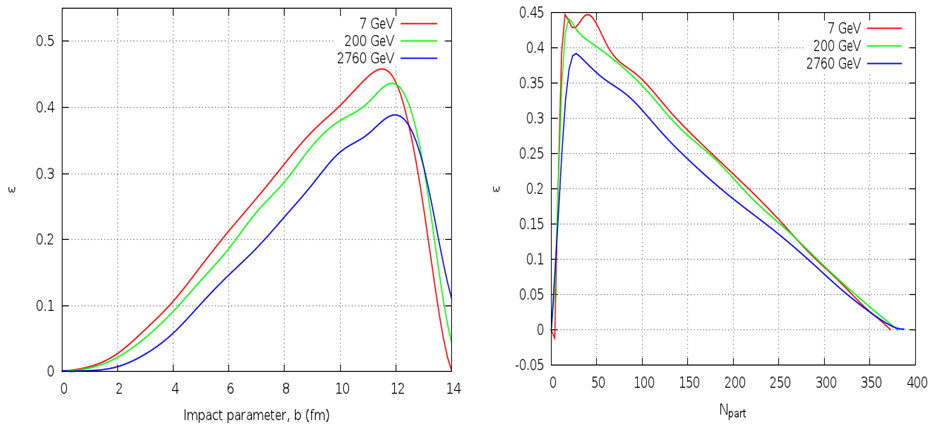 | Figure 9. Eccentricity variation for Au + Au collision at different energies (left): with impact parameter, (right): with  |
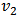 is a measure of this momentum anisotropy and can be expressed as [33]-
is a measure of this momentum anisotropy and can be expressed as [33]-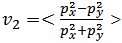 | (5) |
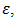 the proportionality is found in between elliptic flow
the proportionality is found in between elliptic flow 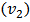 and eccentricity. The Fig.10, is presenting the proportionality relation between the experimentally measured values of
and eccentricity. The Fig.10, is presenting the proportionality relation between the experimentally measured values of 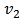 and the spatial anisotropy using Glauber model, for the same centrality as the experimental data [31]. The graph is indicating the transformation from spatial anisotropy to momentum anisotropy clearly for the hot and dense medium created in the heavy-ion collisions. From the observation of the above figure obtained for Au+Au collision it can be guessed that there could be other factors which are affecting the proportionality between the elliptic flow and eccentricity which can dampen this transformation, one of those is viscosity.
and the spatial anisotropy using Glauber model, for the same centrality as the experimental data [31]. The graph is indicating the transformation from spatial anisotropy to momentum anisotropy clearly for the hot and dense medium created in the heavy-ion collisions. From the observation of the above figure obtained for Au+Au collision it can be guessed that there could be other factors which are affecting the proportionality between the elliptic flow and eccentricity which can dampen this transformation, one of those is viscosity. | Figure 10. Plot showing the proportionality between elliptic flow and initial spatial eccentricity for Cu + Cu (left) and Au + Au (right) at 200 GeV [31] |
 are determined by unfolding the statistical fluctuations to azimuthal particle distributions. Then, the by using and calculating the difference in pseudorapidity dependence of flow and non-flow correlations the magnitude of non-flow correlations can be found out [32]. So finally we shall be able to find out the elliptic flow fluctuations by calculating the difference of the contribution of non-flow correlations and the dynamic
are determined by unfolding the statistical fluctuations to azimuthal particle distributions. Then, the by using and calculating the difference in pseudorapidity dependence of flow and non-flow correlations the magnitude of non-flow correlations can be found out [32]. So finally we shall be able to find out the elliptic flow fluctuations by calculating the difference of the contribution of non-flow correlations and the dynamic  fluctuations.
fluctuations.2. Summary & Conclusions
- The elliptic flow is an important parameter which may be a tool to draw the information about the evolution of nuclear collision. Quantitatively the elliptic flow coefficient
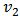 is a measure of the azimuthal anisotropy of particle momenta. The anisotropy depends on the energy and reflects the reaction dynamics. At different energies the elliptic flow changes. A positive
is a measure of the azimuthal anisotropy of particle momenta. The anisotropy depends on the energy and reflects the reaction dynamics. At different energies the elliptic flow changes. A positive 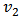 coefficient means the particles are thrown towards the reaction plane preferably by the momentum azimuthal anisotropy, called the in-plane flow, while when
coefficient means the particles are thrown towards the reaction plane preferably by the momentum azimuthal anisotropy, called the in-plane flow, while when 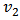 is negative, when the momentum anisotropy pushes particles preferentially perpendicular to the reaction plane defined as the out-of-plane flow. It is found that there is proportionality between eccentricity of the initial geometry of the collision region and the elliptic flow.Ideal hydrodynamics (zero viscosity) is not able to explain the
is negative, when the momentum anisotropy pushes particles preferentially perpendicular to the reaction plane defined as the out-of-plane flow. It is found that there is proportionality between eccentricity of the initial geometry of the collision region and the elliptic flow.Ideal hydrodynamics (zero viscosity) is not able to explain the 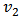 coefficient at all transverse momentum range. Calculations made using hydrodynamics with non-zero shear viscosity η, also the consideration of non-flow effects, and other factors can help to understand the flow fluctuations.The ultra relativistic nuclear collision program is aimed towards the creation of the QGP – quark-gluon plasma – the deconfined state of quarks and gluons at laboratory level. It is very clear that such a state is required to be appearing in a (local) thermalized system achieved by many re-scatterings per particle during the evolution of the system. It is not clear when such a dynamical thermalization can really occur. An understanding of these phenomena can be achieved by considering elliptic flow.
coefficient at all transverse momentum range. Calculations made using hydrodynamics with non-zero shear viscosity η, also the consideration of non-flow effects, and other factors can help to understand the flow fluctuations.The ultra relativistic nuclear collision program is aimed towards the creation of the QGP – quark-gluon plasma – the deconfined state of quarks and gluons at laboratory level. It is very clear that such a state is required to be appearing in a (local) thermalized system achieved by many re-scatterings per particle during the evolution of the system. It is not clear when such a dynamical thermalization can really occur. An understanding of these phenomena can be achieved by considering elliptic flow. Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML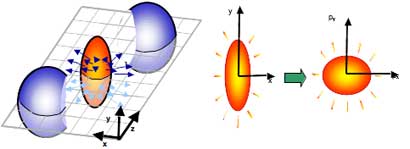
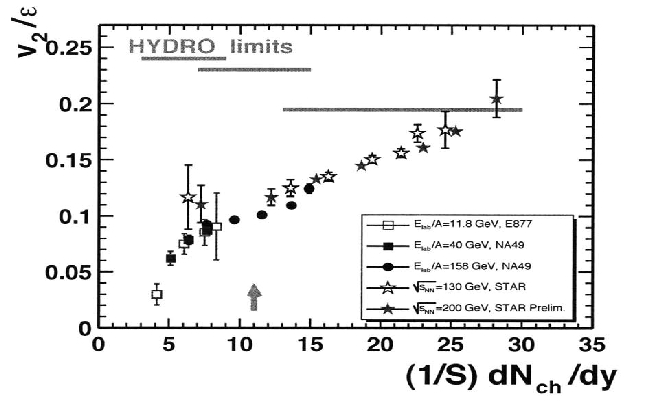
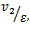 as a function of particle density in the transverse plane, 1/S(dN/dy), for different collision systems, center of mass energies and centrality ranges [24]
as a function of particle density in the transverse plane, 1/S(dN/dy), for different collision systems, center of mass energies and centrality ranges [24]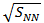 = 200 GeV. Phys. Rev. Lett., 104:062301, 2010. [arXiv:0903.2811].
= 200 GeV. Phys. Rev. Lett., 104:062301, 2010. [arXiv:0903.2811]. = 200 GeV. Phys. Rev. Lett., 95:152301, 2005. [arXiv:nucl-ex/0501016].
= 200 GeV. Phys. Rev. Lett., 95:152301, 2005. [arXiv:nucl-ex/0501016].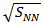 = 200 GeV: Jet-quenching and the response of partonic matter. Phys. Rev., C77:011901, 2008. [arXiv:0705.3238].
= 200 GeV: Jet-quenching and the response of partonic matter. Phys. Rev., C77:011901, 2008. [arXiv:0705.3238].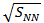 = 200 GeV. Phys. Rev., C78:014901, 2008. [arXiv:0801.4545].
= 200 GeV. Phys. Rev., C78:014901, 2008. [arXiv:0801.4545].