Ali A. Alzubadi1, Z. A. Dakhil1, Sheimaa T. Aluboodi2
1Department of physics, College of Science, University of Baghdad, Iraq
2Dijlah College University, Baghdad, Iraq
Correspondence to: Sheimaa T. Aluboodi, Dijlah College University, Baghdad, Iraq.
| Email: |  |
Copyright © 2014 Scientific & Academic Publishing. All Rights Reserved.
Abstract
In the present research the ground state nuclear structure of Zr-isotopes has been investigated within the framework of Skyrme-Hartree-Fock using the Skyrme parameterizations; SkM*, S1, S3, SkM, and SkX. The charge, proton, neutron and mass densities together with their associated root mean square radii, neutron skin thicknesses, nuclear binding energies, and charge form factors have been calculated. The effects of Skyrme parameterizations on the calculated values of the static nuclear properties of the selected isotopes have been disclosed in appropriate figures. It can be deduced from this research that it is the SkX parameterization which achieves the best agreement with the experimental data as compared with the other parameterizations. Comparison between the theoretical and experimental results of charge form factors has likewise been performed.
Keywords:
Skyrme-Hartree-fock method, Zr-isotopes
Cite this paper: Ali A. Alzubadi, Z. A. Dakhil, Sheimaa T. Aluboodi, Microscopic Study of Nuclear Structure for Some Zr-isotopes Using Skyrme-Hartree-Fock-Method, Journal of Nuclear and Particle Physics, Vol. 4 No. 6, 2014, pp. 155-163. doi: 10.5923/j.jnpp.20140406.01.
1. Introduction
The nuclear density distribution is one of the basic quantities for describing the nuclear structure. It can give detailed information on the internal structure of nuclei since they are directly related to the wave functions of the protons and neutrons which are important keys to many calculations in nuclear physics. Also the nuclear charge radii represent the most useful observables for analyzing the nuclear structure. These observables provide information about the nuclear shape which can be determined from the form factors.In the present research, the ground state properties of Zr-isotopes will be investigated in details using Skyrme-Hartree-Fock (SHF) method which has been used successfully to describe the ground state properties of stable nuclei [1-3]. In particular, we will investigate the static nuclear properties namely, the charge, proton, neutron and mass densities together with their associated root mean square (rms) radii, neutron skin thicknesses, total nuclear binding energies, and charge form factors. The calculated results will then be compared with the available experimental data for the said isotopes.
2. Theory and Methodology
The Skyrme effective interaction was first proposed in the work of Vautherin and Brink [4]. It was introduced in the Hartree-Fock (HF) calculations of nuclei [5]. Until now, the SHF method has been successfully and widely used for studying the nuclear structure [2]. The Skyrme force is an effective interaction with a two-body and a three-body parts [6]. The two body term is written as a short range expansion in the form [7]: 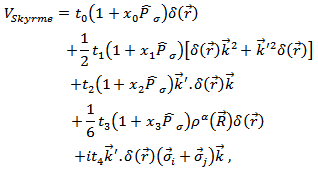 | (1) |
where the 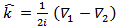 and
and 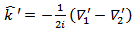 operators are the relative (momentum) wave vectors of two nucleons.
operators are the relative (momentum) wave vectors of two nucleons.  acts to the right and
acts to the right and 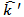 to the left.
to the left. 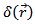 is the delta function.
is the delta function. 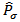 is the space exchange operator,
is the space exchange operator, 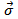 the vector of Pauli spin matrices and the
the vector of Pauli spin matrices and the 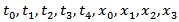 and
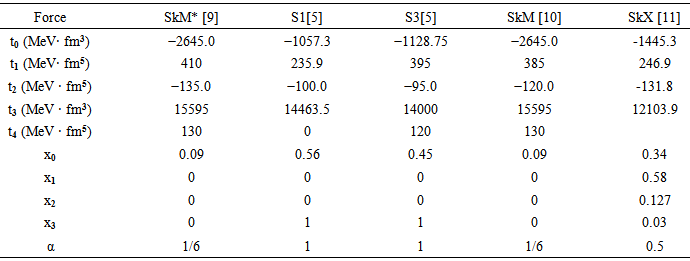
and 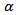 are the Skyrme force parameters describing the strengths of the different interaction terms [8]. The values of these parameters for different parameterizations are listed in Table.1.
are the Skyrme force parameters describing the strengths of the different interaction terms [8]. The values of these parameters for different parameterizations are listed in Table.1.Table 1. The Skyrme parameterizations that have been used in the present research
 |
| |
|
The Hamiltonian is written in terms of kinetic energy and two-body nucleon-nucleon interaction [12]: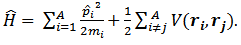 | (2) |
In this representation of the Hamiltonian the nucleon-nucleon interaction characterizes the many-particle Schrodinger equation. In the SHF approach the total binding energy of the system is given by the sum of the kinetic and Coulomb energies as well as the Skyrme energy functional that models the effective interaction between nucleons [13]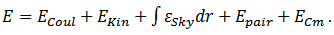 | (3) |
By substituting the Skyrme interaction terms into the full energy expression, the form of the density function 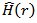 can be written as [14].
can be written as [14].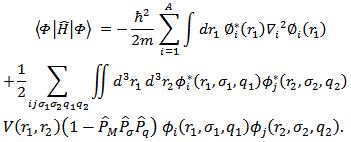 | (4) |
The ground-state charge density 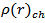 , gives the most direct physical insight into the distribution of protons inside the nucleus. The densities in spherical representation are given by [15]:
, gives the most direct physical insight into the distribution of protons inside the nucleus. The densities in spherical representation are given by [15]: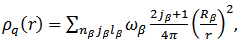 | (5) |
where 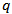 represents the neutron, proton and charge,
represents the neutron, proton and charge, 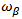 is the occupation probability of the state
is the occupation probability of the state 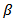 and
and 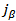 is the current density that vanishes for the ground states. The charge probability density [16].
is the current density that vanishes for the ground states. The charge probability density [16].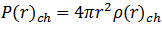 | (6) |
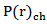 represents the probability to find Z protons at a given radius r from the center of the nucleus. The rms radii of neutron, proton, charge and mass distributions can be evaluated from these densities as [17]:
represents the probability to find Z protons at a given radius r from the center of the nucleus. The rms radii of neutron, proton, charge and mass distributions can be evaluated from these densities as [17]: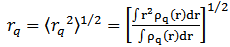 | (7) |
where q = neutron, proton or charge. A quantity of both theoretical and experimental interest, the neutron skin thickness t, can then be defined as the difference between the neutron rms radius and the proton rms radius [18]: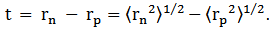 | (8) |
The concept of form factor is associated with the charge density and its properties. Elastic electron scattering from nuclei constitutes an important source of experimental data on charge densities which are measurable and with which the models for nuclear ground states can be tested. Electron scattering evolved from the early determinations of rms charge radii to the present much more precise measurements that have led to almost model- independent determinations of the charge density distributions of many nuclei. In these density distributions one can observe oscillations in the interior density which oscillations represent quantum “waves” in the nucleus [19]. Denoting by 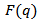 the ratio of the electron scattering cross section to the Rutherford cross section (scattering from a point) as a function of momentum transfer, q, one will find that this ratio expresses the plane-wave Fourier transform of the charge density as follows [17]:
the ratio of the electron scattering cross section to the Rutherford cross section (scattering from a point) as a function of momentum transfer, q, one will find that this ratio expresses the plane-wave Fourier transform of the charge density as follows [17]: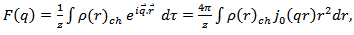 | (9) |
where the spherical Bessel function is: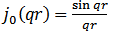 | (10) |
The normalization in Eq. (9) is chosen to give 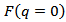 =1. For light nuclei the electron energy distortion is small, and the cross section is closely proportional to the form factor
=1. For light nuclei the electron energy distortion is small, and the cross section is closely proportional to the form factor 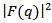 which has minima corresponding to the zeros of the function
which has minima corresponding to the zeros of the function 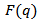 . For heavy nuclei the electron energy distortion is larger and the minima in the cross sections disappear. From an analysis of the electron scattering cross section the ratio
. For heavy nuclei the electron energy distortion is larger and the minima in the cross sections disappear. From an analysis of the electron scattering cross section the ratio 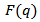 can be extracted with good precision over the range of momentum transfers measured. Consequently, from the measured form factors
can be extracted with good precision over the range of momentum transfers measured. Consequently, from the measured form factors 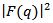 the charge density can be obtained with the inverse of Eq. (9) [19]:
the charge density can be obtained with the inverse of Eq. (9) [19]: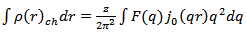 | (11) |
Since the form factors data are only determined up to some 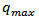 the resulting charge density has some “error band” which depends on the assumptions made about
the resulting charge density has some “error band” which depends on the assumptions made about 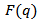 for
for 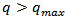 .
.
3. Results and Discussion
We will employ the experimental data on charge density available for the isotope 90Zr taken from Ref. [8]. The density distribution of 90Zr isotope has been calculated using five selected parameterizations and shown in Figs.(1) and (2). Inspection of the charge density profiles reveal that the best agreement between the calculated and experimental data is obtained using the SkX- parameterizations shown in Fig.(1a).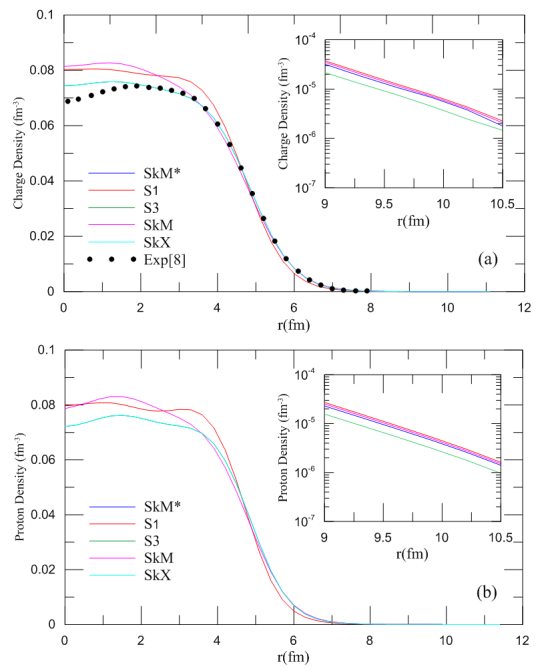 | Figure (1). Density profiles of  -isotopes as functions of radii calculated using different Skyrme parameterizations; (a) charge (b) protons -isotopes as functions of radii calculated using different Skyrme parameterizations; (a) charge (b) protons |
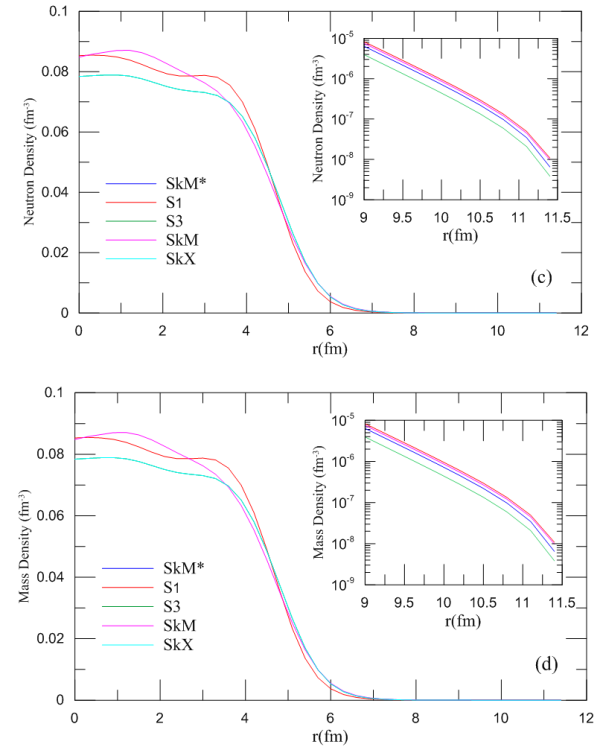 | Figure (2). Density profiles of 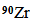 -isotopes as functions of radii calculated using different Skyrme parameterizations; (c) neutrons (d) mass -isotopes as functions of radii calculated using different Skyrme parameterizations; (c) neutrons (d) mass |
Consequently we applied the SkX-parameterization to all the other Zr-isotopes. The values thus obtained for the charge density of these isotopes at the center, r = 0, decrease with the increasing number of neutrons approximately from (0.082371) fm-3 for 78Zr to (0.067104) fm-3 for 102Zr as shown in Fig. (3a) And the proton density decreases with the increasing neutron number approximately from (0.0827) fm-3 for 78Zr to (0.067764) fm-3 for 102Zr as shown in Fig. (3b). 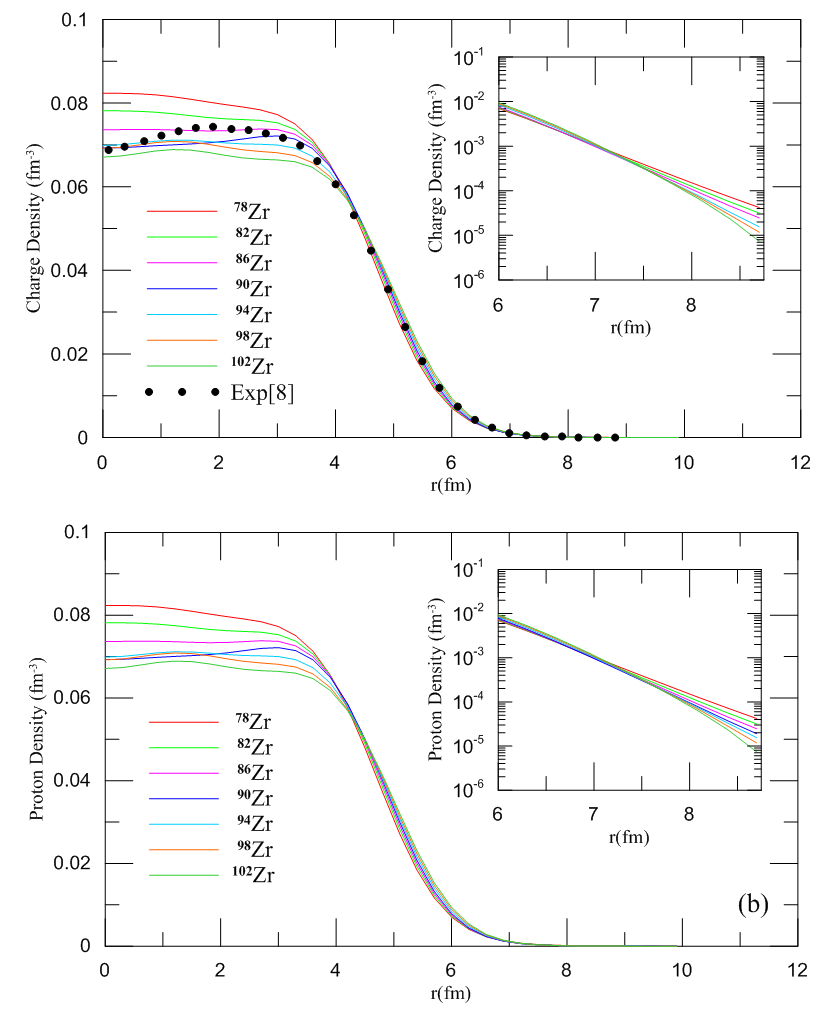 | Figure (3). Density profiles of Zr-isotopes as functions of radii calculated using SkX parameterizations; (a) charge (b) protons |
In general point of view, it can be noted that with increasing number of neutrons in the succeeding isotopes of the same element the neutron density increases whereas the proton density decreases accordingly. This behavior applies to the range range r >1.8 fm, but is violated for the range 0 ~ 1.8 fm, as can be seen clearly in Fig. (4a). The mass density is also governed by the same behavior which applies to the range r > 3.2 fm but is violated for the range r ≤ 3.2 fm as in Fig. (4b). In this range the abnormality (randomness) in the behavior of the isotopes (i.e. oscillations in density values) is due to the diffusion of the nuclear matter in the vicinity of the center of the nucleus. This abnormal behavior results from the stretching of the density distribution as the isotopes increase progressively in mass number. Consequently, the applied Skyrme parameterization fails to give an exact description in the said region.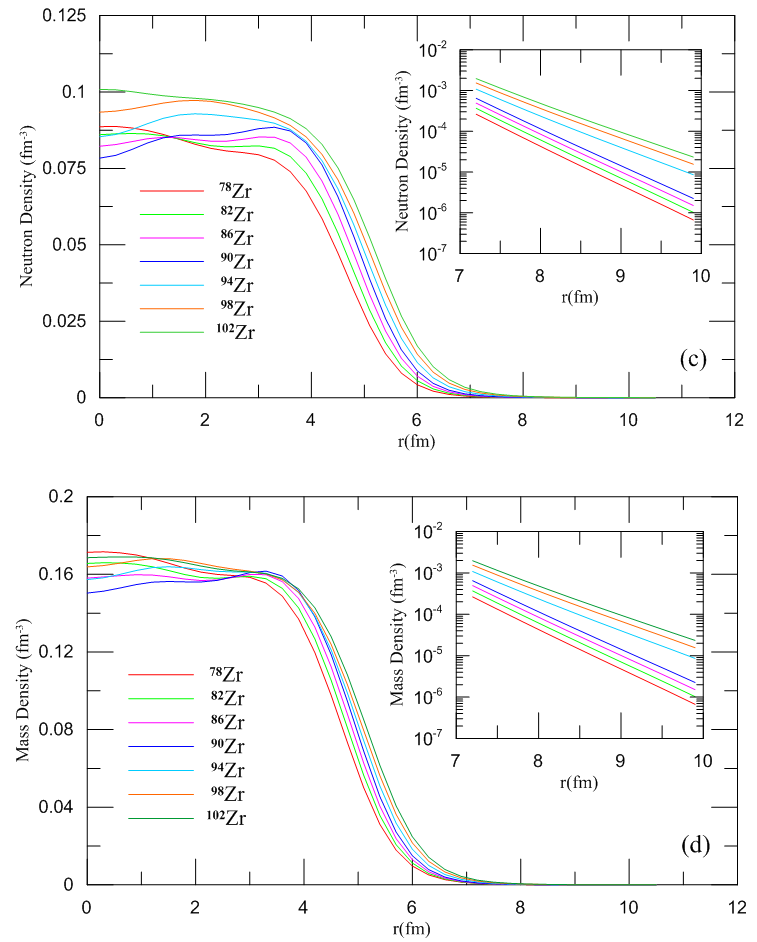 | Figure (4). Density profiles of Zr- isotopes as functions of radii calculated using SkX parameterization; (c) neutron (d) mass |
For more illustration the calculated charge density distributions for Si-isotopes are displayed as a surface in Fig. (5). These distributions are plotted against the nuclear masses which are decreasing (in viewing into the page). These variations of charge densities are best portrayed in block form.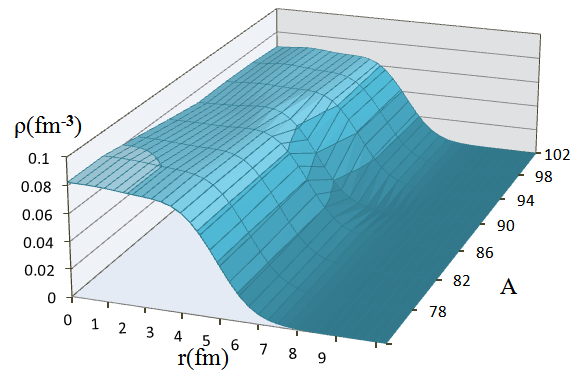 | Figure (5). Charge density variation with mass number A from SkX parameterization for different Zr-isotopes |
Although experimental data on charge probability density may not be available, it can, however, be easily calculated from the experimental data already available on nuclear charge density that was employed in calculating the probability densities. The calculated and experimental charge probability densities of the 90Zr are in good agreement as shown clearly in Fig. (6). 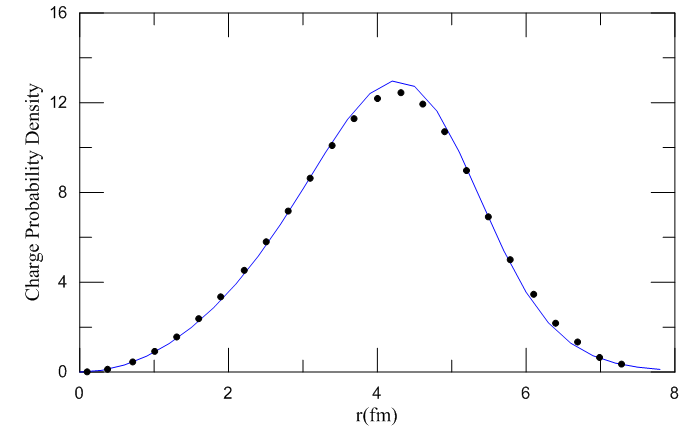 | Figure (6). Charge probability density distributions for  isotope using SkX parameterization isotope using SkX parameterization |
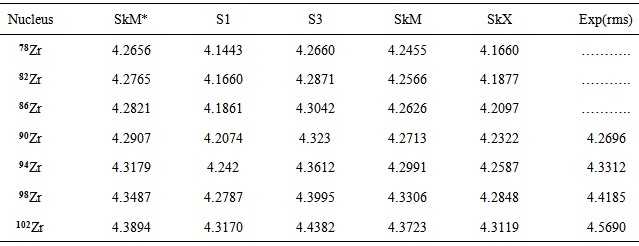
The rms charge radius is a fundamental property of the atomic nucleus. The rms radii of charge distributions can be evaluated from the charge densities according to Eq. (7). As can be seen from Table 2 below the calculations by the SHF- method of the nuclear charge rms radii of the Zr isotopes reveal a good conformity among the values in each row separately i.e., for each isotope, and in all the rows combined. All the values based on the different parameter sets considered in the table have more or less the same value. The rms charge radii for 78 Zr and 102 Zr decrease only slightly from (4.2656) and (4.3894) by SkM* to (4.1443) and (4.3170) by S1 as shown below.Table 2. Calculation of nuclear charge rms radii compared with experimental data from Ref. [17]
 |
| |
|
As to the nuclear binding energies, Fig. (7) shows a comparison between the experimental and theoretical values for the Zr-isotopes. The Skyrme parameterizations SkM*, S1, S3, SkM, and SkX are used in the calculations. Except for some slight deviations in the S1- curve all the other curves generally show the same behavior wherein the binding energy increases with increasing mass number. 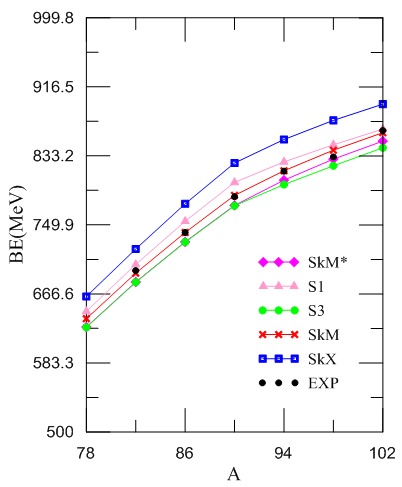 | Figure (7). The binding energy of Zr-isotopes calculated using different Skyrme parameterizations |
The SkM* based binding energies have the highest values for all the isotopes of each of the four element whereas the S3 values are the lowest. The SkM binding energy values turn out to be in full agreement with the experimental data as can be clearly seen in Table 3. For this reason we have selected the SkM parameterization as a basis for calculating the form factors of the selected nuclides.Table 3. Calculated values of Binding energy compared with experimental data from Ref. [20]
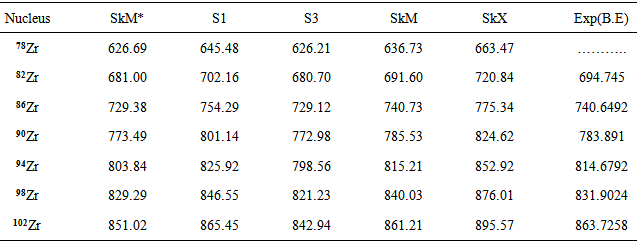 |
| |
|
The skin thickness of a nucleus is defined as the distance over which the charge density drops from 90% to 10% of its maximal value. The thickness is almost the same for all heavy nuclei and is given by: t = 2a ln 9 ~ 2.40 fm [21]. The growth of the neutron skin with increasing neutron number was calculated for several isotopes from nuclear and charge-size data [22]. The neutron skin thickness of Zr isotopes increases with increasing mass number along all the curves plotted by the different Skyrme parameterizations as shown in Fig. (8). In Table 4 the quantity t for some of the isotopes have negative values because the force tend to spread the protons a little and becomes increase in positive with increasing the neutron excess.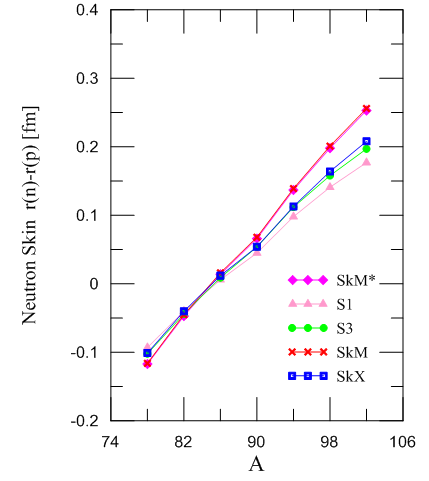 | Figure (8). The neutron skin thickness of Zr-isotopes calculated using different Skyrme parameterizations |
Table 4. The skin thickness of Zr isotopes calculated using different Skyrme parameterizations
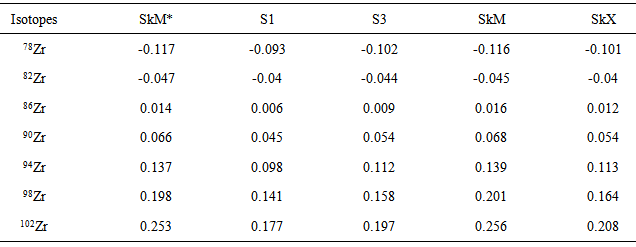 |
| |
|
From the charge densities shown in Fig. (2a), the scattering amplitude form factors 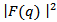 were calculated for the Zr-isotopes and shown in Fig. (9). In this figure the hollow circles stand for the experimental data [16] given over the range of momentum transfers measured experimentally. The said experimental data were then compared with the theoretical values of the form factors calculated using the SkX parameterization. It is found that there is a fine agreement in the range of momentum transfer ≤ 2.4 fm-1. For greater values, the theoretical values deviate and become less than the experimental data.
were calculated for the Zr-isotopes and shown in Fig. (9). In this figure the hollow circles stand for the experimental data [16] given over the range of momentum transfers measured experimentally. The said experimental data were then compared with the theoretical values of the form factors calculated using the SkX parameterization. It is found that there is a fine agreement in the range of momentum transfer ≤ 2.4 fm-1. For greater values, the theoretical values deviate and become less than the experimental data. 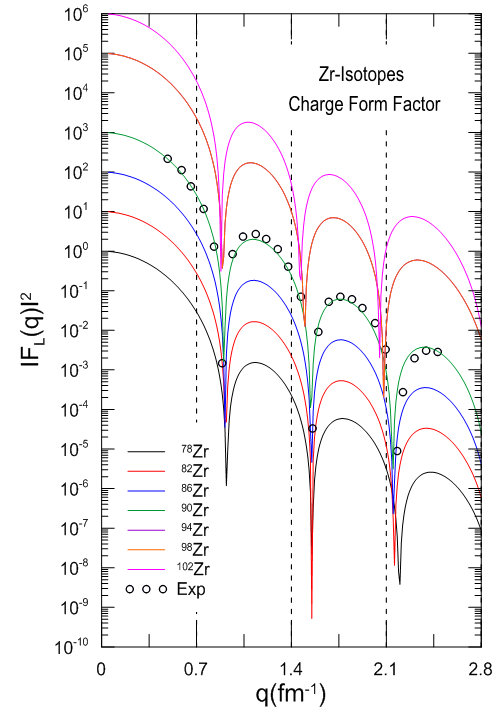 | Figure (9). Charge form factors versus momentum transfer q(fm-1) for  and and   isotopes. The experimental data are taken from Ref. [16] isotopes. The experimental data are taken from Ref. [16] |
This deviation is ascribed to two factors. First, the Skyrme interaction approximation undergoes a low-momentum expansion, and the density fluctuation resulting from this approximation is expected to break down at some point. Second, mesonic-exchange corrections to the charge form factor become increasingly important at higher momentum transfers [18].
4. Conclusions
The above calculations show that the best agreement between the theoretical values and experimental data is better achieved for nuclear charge density by the SkX parameterization than by the others. However in the vicinity of the nucleus center (on the range r < 2 fm) the isotopes behave randomly with oscillating density values due to the diffusion (stretching) of the nuclear matter, which makes Skyrme parameterizations fail to give an exact description in the said region. As to the binding energy the best agreement between calculations and experimental data is achieved by SkM parameterization. The comparison between experiment and theory in terms of form factors have been discussed, where the data are taken over the range of momentum measured, and in terms of the charge densities. Rapid oscillations may occur in the experimental densities. Comparison with experiment will provide a test for the mean-field models.
References
| [1] | J.W. Negele and D. Vautherin, Phys. Rev. C5 (1972)1472. |
| [2] | J. Friedrich and P.-G. Rienhard, Phys. Rev. C33 (1986) 335. |
| [3] | J. Dobaczewski, I. Hamamoto, W. Nazarewicz and J.A. Sheikh, Phys. Rev. Lett. 72(1994)981. |
| [4] | T. H. Skyrme, Phil. Mag. 1 (1956) 1043; Nucl. Phys. 9 (1959) 615. |
| [5] | D. Vautherin and D. M. Brink, Phys. Rev. C5 (1972) 626. |
| [6] | Skyrme, T. The Effective Nuclear Potential. Nuclear Physics, 9 (1959) 615. |
| [7] | W. Greiner and j. Maruhn, “Nuclear Models” 2nd Ed., Springer-verlge Berlin (1996). |
| [8] | L.G. Qiang, J. Phys. G 17 (1991) 134. |
| [9] | J. Bartel, P. Quentin, M. Brack, C. Guet and M.B. Hakansson, Nucl. Phys. A386 (1982) 79. |
| [10] | L.X. Ge, Y.Z. Zhuo, and W. Norenberg, Nucl. Phys. A459 (1986) 77. |
| [11] | B.A. Brown, Phys. Rev. C58 (1998) 220. |
| [12] | E. Suckling, PhD thesis, University of Surrey (2011). |
| [13] | M. Bender, P. H. Heenen and P. G. Reinhard, Rev. Mod. Phys. 75 (2003) 121. |
| [14] | E. Suckling, MsC thesis, University of Surrey (2006). |
| [15] | K. Langanke, J.A. Maruhn and S. E. Koonin, Computational Nuclear Physics 1, Springer-Verlag (1991). |
| [16] | W. A. Richter and B. A. Brown, Phys. Rev., C67 (2003) 034317. |
| [17] | I. Angeli, At. Data Nucl. Data Tab. 78 (2004) 185. |
| [18] | M. Brack, C. Guet and H. B. Hakansson, Phys. Lett. 5 (1985) 36. |
| [19] | H. Uberall “Electron Scattering From Complex Nuclei (part A)” Academic Press-New York and London (1971). |
| [20] | Y.S. Shen and Z.Z. Ren, Phys. Rev., C54 (1996) 1158. |
| [21] | I. C. Brock, Physik V: Nuclear and Particle Physic (2012) 135. |
| [22] | A. Ozawa, T. Suzuki and I. Tanihata, Nucl. Phys. A693 (2001) 32. |

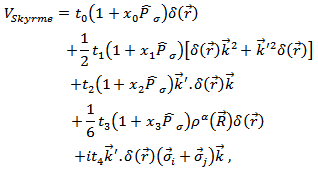
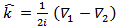 and
and 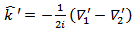 operators are the relative (momentum) wave vectors of two nucleons.
operators are the relative (momentum) wave vectors of two nucleons. 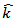 acts to the right and
acts to the right and 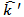 to the left.
to the left. 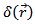 is the delta function.
is the delta function. 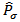 is the space exchange operator,
is the space exchange operator, 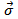 the vector of Pauli spin matrices and the
the vector of Pauli spin matrices and the 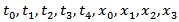 and
and 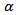 are the Skyrme force parameters describing the strengths of the different interaction terms [8]. The values of these parameters for different parameterizations are listed in Table.1.
are the Skyrme force parameters describing the strengths of the different interaction terms [8]. The values of these parameters for different parameterizations are listed in Table.1.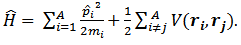
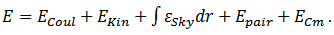
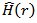 can be written as [14].
can be written as [14].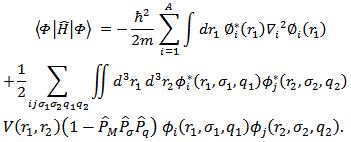
 , gives the most direct physical insight into the distribution of protons inside the nucleus. The densities in spherical representation are given by [15]:
, gives the most direct physical insight into the distribution of protons inside the nucleus. The densities in spherical representation are given by [15]: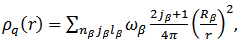
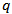 represents the neutron, proton and charge,
represents the neutron, proton and charge, 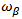 is the occupation probability of the state
is the occupation probability of the state 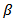 and
and 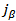 is the current density that vanishes for the ground states. The charge probability density [16].
is the current density that vanishes for the ground states. The charge probability density [16].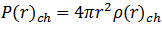
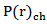 represents the probability to find Z protons at a given radius r from the center of the nucleus. The rms radii of neutron, proton, charge and mass distributions can be evaluated from these densities as [17]:
represents the probability to find Z protons at a given radius r from the center of the nucleus. The rms radii of neutron, proton, charge and mass distributions can be evaluated from these densities as [17]: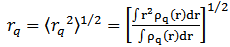
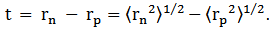
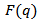 the ratio of the electron scattering cross section to the Rutherford cross section (scattering from a point) as a function of momentum transfer, q, one will find that this ratio expresses the plane-wave Fourier transform of the charge density as follows [17]:
the ratio of the electron scattering cross section to the Rutherford cross section (scattering from a point) as a function of momentum transfer, q, one will find that this ratio expresses the plane-wave Fourier transform of the charge density as follows [17]: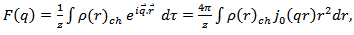
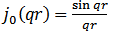
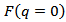 =1. For light nuclei the electron energy distortion is small, and the cross section is closely proportional to the form factor
=1. For light nuclei the electron energy distortion is small, and the cross section is closely proportional to the form factor 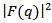 which has minima corresponding to the zeros of the function
which has minima corresponding to the zeros of the function 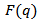 . For heavy nuclei the electron energy distortion is larger and the minima in the cross sections disappear. From an analysis of the electron scattering cross section the ratio
. For heavy nuclei the electron energy distortion is larger and the minima in the cross sections disappear. From an analysis of the electron scattering cross section the ratio 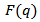 can be extracted with good precision over the range of momentum transfers measured. Consequently, from the measured form factors
can be extracted with good precision over the range of momentum transfers measured. Consequently, from the measured form factors 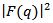 the charge density can be obtained with the inverse of Eq. (9) [19]:
the charge density can be obtained with the inverse of Eq. (9) [19]: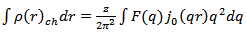
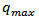 the resulting charge density has some “error band” which depends on the assumptions made about
the resulting charge density has some “error band” which depends on the assumptions made about 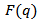 for
for 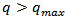 .
.
 -isotopes as functions of radii calculated using different Skyrme parameterizations; (a) charge (b) protons
-isotopes as functions of radii calculated using different Skyrme parameterizations; (a) charge (b) protons
 -isotopes as functions of radii calculated using different Skyrme parameterizations; (c) neutrons (d) mass
-isotopes as functions of radii calculated using different Skyrme parameterizations; (c) neutrons (d) mass



 isotope using SkX parameterization
isotope using SkX parameterization

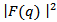 were calculated for the Zr-isotopes and shown in Fig. (9). In this figure the hollow circles stand for the experimental data [16] given over the range of momentum transfers measured experimentally. The said experimental data were then compared with the theoretical values of the form factors calculated using the SkX parameterization. It is found that there is a fine agreement in the range of momentum transfer ≤ 2.4 fm-1. For greater values, the theoretical values deviate and become less than the experimental data.
were calculated for the Zr-isotopes and shown in Fig. (9). In this figure the hollow circles stand for the experimental data [16] given over the range of momentum transfers measured experimentally. The said experimental data were then compared with the theoretical values of the form factors calculated using the SkX parameterization. It is found that there is a fine agreement in the range of momentum transfer ≤ 2.4 fm-1. For greater values, the theoretical values deviate and become less than the experimental data. 
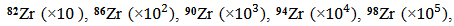 and
and 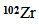
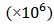 isotopes. The experimental data are taken from Ref. [16]
isotopes. The experimental data are taken from Ref. [16] Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML


