-
Paper Information
- Previous Paper
- Paper Submission
-
Journal Information
- About This Journal
- Editorial Board
- Current Issue
- Archive
- Author Guidelines
- Contact Us
Journal of Nuclear and Particle Physics
p-ISSN: 2167-6895 e-ISSN: 2167-6909
2014; 4(5): 147-153
doi:10.5923/j.jnpp.20140405.03
Foundation of Complex Matter Space and Special Theory of Relativity, a Unifying Approach
Reza Ahangar
Department of Mathematic, Texas A & M University-Kingsville, Kingsville, USA
Correspondence to: Reza Ahangar, Department of Mathematic, Texas A & M University-Kingsville, Kingsville, USA.
| Email: |  |
Copyright © 2014 Scientific & Academic Publishing. All Rights Reserved.
Relativistic mechanics cannot recognize speed faster than light. In this article, a new fundamental view on matter will be presented and the paradigm will be shifted from real or pure imaginary particle to Complex Matter Space. We will investigate the relativistic concept of Complex Matter Space. A new assumption will be imposed that matter has two intrinsic components, i) mass, and ii) charge. The mass will be measured by a real number and charge by an imaginary unit. We are hoping that this approach will help us to present a relativistic view of energy and momentum in Complex Matter Space. We will conclude that the new Complex Matter Space (CMS) theory will help get one step closer to a better understanding toward, 1) the conversion of mass and energy 2) Energy and Momentum, 3) unifying the forces, 4) tachyon, dark energy & dark matter, and also antiparticles.
Keywords: Complex Matter, complex Energy, and Complex Momentum
Cite this paper: Reza Ahangar, Foundation of Complex Matter Space and Special Theory of Relativity, a Unifying Approach, Journal of Nuclear and Particle Physics, Vol. 4 No. 5, 2014, pp. 147-153. doi: 10.5923/j.jnpp.20140405.03.
Article Outline
1. Complex Matter a New View of Imaginary Mass and Charges
- Using Doppler Shift phenomena, scientists can learn much about the motion of galaxies. It is known that the light from one side of the galaxy is blue shifted and the light from the other side is red shifted. This indicates that one side is moving toward the earth, and the other is moving away. All these will help us to determine the speed at which the galaxy is rotating. Using the frequency of the rotation can help estimate masses in galaxies. Dark energy was first proposed in 1998 when two groups of astronomers made a survey of exploding stars or supernovas in distant galaxies. These cosmological observations strongly suggest that the universe is dominated by dark energy. Both dark energy and dark matter are not distinct, but are a unique entity of matter (Shibili -2007).Recent observations by NASA agree that dark energy and dark matter represent one entity and have densities close to the range 10-26 kg/m3. The ratio between energy density (in Joules) and the mass density (kg/m3) are proportional to the square of the speed of light. (Shibli 2006 & 2007).The content of the paper on "Imaginary Relativity" is a right direction toward Complex Matter Space (CMS) but not sufficient for the unifying forces (Rezaei 2010). The CMS postulates may answer some of the questions in this article's concluding remarks. This could be a reason for the statement "the author does not know where the imaginary world is located or what its nature is?".It is important to postulate that matter has two components that can be demonstrated in a complex plane as a real component and an imaginary component:
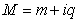 | (1.1) |
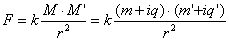 | (1.2) |
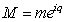 . One can explore and study the implication of this assumption, and demonstrate the consistency with other phenomenon, theories, or experiments.The existence of a particle traveling faster than light has been presented by many authors including, Sudarshan 1970 who discussed the Physics of complex mass.The organization of this paper is the following: A new View of complex matter will be presented based on two new postulates. A geometric interpretation of Complex Matter will be used to justify them in a complex coordinate plane.By these new assumptions of Mass and Energy, Newtonian Mechanics will be restructured in section two. In section three we will observe Newtonian Mechanics in Complex Matter Space and challenges in Imaginary Mass, Force, Acceleration, and Momentum.In this relativistic view of Complex Matter, Einstein's equation of mass-energy will be revised.The relativistic view of the complex Matter Space will be investigated in section four. In section five the derivation of Einstein's equation in complex matter space will be presented. The relativistic view of energy will be discussed in section six.Finally, energy and momentum will be recalculated in the Complex space. In section seven, we will explore a possible explanation of the Existence of Negative Matter and Antimatter, as well as dark energy and dark matter. Further possible investigation and research will be presented.
. One can explore and study the implication of this assumption, and demonstrate the consistency with other phenomenon, theories, or experiments.The existence of a particle traveling faster than light has been presented by many authors including, Sudarshan 1970 who discussed the Physics of complex mass.The organization of this paper is the following: A new View of complex matter will be presented based on two new postulates. A geometric interpretation of Complex Matter will be used to justify them in a complex coordinate plane.By these new assumptions of Mass and Energy, Newtonian Mechanics will be restructured in section two. In section three we will observe Newtonian Mechanics in Complex Matter Space and challenges in Imaginary Mass, Force, Acceleration, and Momentum.In this relativistic view of Complex Matter, Einstein's equation of mass-energy will be revised.The relativistic view of the complex Matter Space will be investigated in section four. In section five the derivation of Einstein's equation in complex matter space will be presented. The relativistic view of energy will be discussed in section six.Finally, energy and momentum will be recalculated in the Complex space. In section seven, we will explore a possible explanation of the Existence of Negative Matter and Antimatter, as well as dark energy and dark matter. Further possible investigation and research will be presented. 2. Overview of Complex Matter SPACE (CMS)
- Assume that the terminology "matter" in general is an undefined term. In this paper, in addition to the postulates of Special Relativity Theory (SRT) we accept the following new postulates:Postulate (I): mass and charge are two intrinsic components of matter and they can be measured, described, and determined in a complex plane. The real part is equal to the mass and the imaginary part is the charge of the particle. That is M=m+iq.Postulate (II): In one dimensional space, position and velocity are assumed to be real numbers.By accepting the second postulate of CMS we are admitting that the particle can be selected in a complex plane and the velocity of a particle can be assumed to be faster than the speed of light.The position x(t) and the velocity dx/dt will stay a real number. The speed of light remains a constant real number, c. By this agreement, and contrary to the paper "Imaginary Relativity" by Rezaei (Rezaei 2010), we are not accepting variation of the speed of light or considering it as a complex number. In addition the complex plane of (t,E) is not an ordered set. Thus, using the Heisenberg Principle

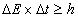 should be adjusted to a real number.For decades, the discovery of the nature of other forces was a dream.Acceptance of this postulate leads to the necessity to reaffirm the entire physics, Newtonian Mechanics, Relativity, and Quantum mechanics.
should be adjusted to a real number.For decades, the discovery of the nature of other forces was a dream.Acceptance of this postulate leads to the necessity to reaffirm the entire physics, Newtonian Mechanics, Relativity, and Quantum mechanics.2.1. Pure Imaginary Unit for Time in 4D–Space
- Absolute time may be an undefined word and we try to postulate, define, and measure it by its changes, variations, and motions with other physical quantities in space. Physical motion of particles, rotation of the earth around the sun, or clock's hands on a circle. The unit of time practically is what we perceive about how much physical objects change position, velocity, energy, or mass. How do we define one hour, one minute, or one second? They are the measurements of the physical changes that we try to demonstrate by arc-length on a clock using the unit of distance or radians on a circle.Are they real measurements of the time? In the following mathematical argument we introduce
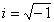 as a unit of time on the imaginary axis.Let us consider a vector
as a unit of time on the imaginary axis.Let us consider a vector 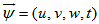 such that
such that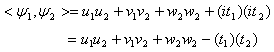 | (2.1) |
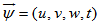

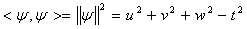
2.2. Verifying the CMS Postulate (II)
- According to time and length dilation in SRT, the value of time and length variation
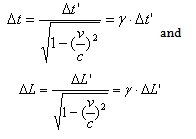 | (2.2) |
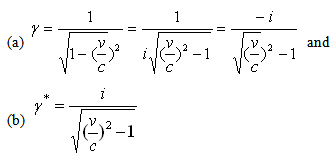 | (2.3) |

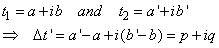 where we replaced, p=a’-a, q=b’-b. The relation (2.2) can be expressed by
where we replaced, p=a’-a, q=b’-b. The relation (2.2) can be expressed by
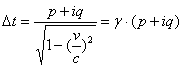 Case (I): the motion velocity v<c.The values of
Case (I): the motion velocity v<c.The values of 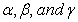 will remain real numbers. Consequently according to (2.2) velocity v and distance L will be real numbers.
will remain real numbers. Consequently according to (2.2) velocity v and distance L will be real numbers.
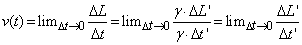 Case (II): If the particle velocity is faster than the speed of light (v>c) then both
Case (II): If the particle velocity is faster than the speed of light (v>c) then both 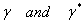 are pure imaginary numbers and using (2.8) the following show that
are pure imaginary numbers and using (2.8) the following show that
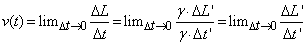 is a real number.This argument infers that the inequality v>c demonstrates the relation in an ordered set. This is not true in the complex plane (see Naber 1992).
is a real number.This argument infers that the inequality v>c demonstrates the relation in an ordered set. This is not true in the complex plane (see Naber 1992).3. Complex Matter in Newtonian Mechanics
- Having a new unified presentation of mass and charge in the form of Complex Matter will bring a new question and challenges in force, acceleration, energy, and momentum. How do we interpret the principles of Newtonian Mechanics?a) Newton's First: If no net force acts on a body its acceleration is zero.It is assumed that when an object is under the influence of a force, if the object is at rest it stays at rest and if it is in motion the motion will be uniform.Further investigation is required to clarify the terminology of undefined term and consistency with other Newtonian mechanics.b) Newton's Second Law: It is proven that many different Forces exerted on an object cause changes in the position of the object and create a variety of accelerations in the motion and of the object.The second of Newton's Laws of motion of an object will be
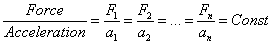 | (3.1) |
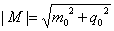 and
and 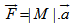 where
where 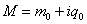 is in the complex plane, m0 is mass at rest, and q0 is the charge of the initial particle.The alternative way to express Newton's Law for complex matter will be
is in the complex plane, m0 is mass at rest, and q0 is the charge of the initial particle.The alternative way to express Newton's Law for complex matter will be | (3.2) |
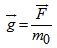 and for electric fields will be
and for electric fields will be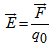 .The unit dimension of g is usually written as meters/sec2, but could be written as nt/kg. The unit dimension for E is written as (Newtons/ Coulomb) nt/coul. Example: A particle of mass m and charge q is placed at rest in a uniform electric field m and released. Its motion can be described
.The unit dimension of g is usually written as meters/sec2, but could be written as nt/kg. The unit dimension for E is written as (Newtons/ Coulomb) nt/coul. Example: A particle of mass m and charge q is placed at rest in a uniform electric field m and released. Its motion can be described 
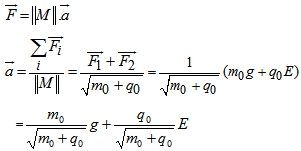 The unit for the measurement is a linear combination of g and E. This process is the resultant of two vectors of gravitation and charge.Traveling Beyond the Speed of Light: We may not be allowed to cross the boundary of the speed of light c in the real world. However, if we can pretend that we are existing in the imaginary world then we are allowed to go faster than light, since our conjugate space will be the real world. Assume that we are traveling by a rocket which is taking off from the earth and wishes to go cruising in space. How much energy is required to accelerate to the speed of light? it would be impossible for a particle to be accelerated to c because the speed of light is constant in a vacuum for all inertial observers. What do we observe? i) Observers in all inertial frames on the earth would measure the same value for c and in fact infinite energies are required to accelerate objects to the speed of light.ii) If we can break the wall of speed of light and travel faster than light, an observer would see things going crazy around – by SRT time dilation the time would freeze around us, - mass will approach infinity.
The unit for the measurement is a linear combination of g and E. This process is the resultant of two vectors of gravitation and charge.Traveling Beyond the Speed of Light: We may not be allowed to cross the boundary of the speed of light c in the real world. However, if we can pretend that we are existing in the imaginary world then we are allowed to go faster than light, since our conjugate space will be the real world. Assume that we are traveling by a rocket which is taking off from the earth and wishes to go cruising in space. How much energy is required to accelerate to the speed of light? it would be impossible for a particle to be accelerated to c because the speed of light is constant in a vacuum for all inertial observers. What do we observe? i) Observers in all inertial frames on the earth would measure the same value for c and in fact infinite energies are required to accelerate objects to the speed of light.ii) If we can break the wall of speed of light and travel faster than light, an observer would see things going crazy around – by SRT time dilation the time would freeze around us, - mass will approach infinity.4. Relativistic View of the Complex Matter SPACE
- Antimatter: A substance composed of elementary particles having the mass and electric charge of ordinary matter (such as electrons and protons) but for which the charge and related magnetic properties are opposite in sign. The existence of antimatter was posted by the electron theory of P.A.M. Dirac. In 1932 the positron (antielectron) was detected in cosmic rays, followed by the antiproton and the antineutron detected through the use of particle accelerators. Positrons, antiprotons, and antineutrons, collectively called antiparticles, are the antiparticles of electrons, protons, and neutrons, respectively. When matter and antimatter are in close proximity, annihilation occurs within a fraction of a second, releasing large amounts of energy. The (relativistic) mass of an object measured by an observer in the xyz-frame is given by
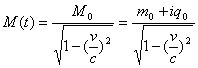 | (4.1) |
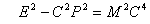 | (4.2) |
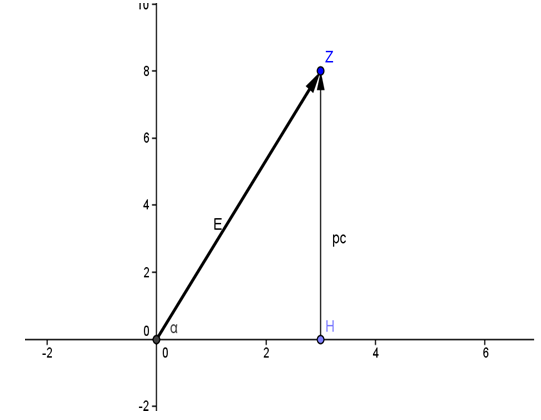 | Figure (1). Energy-momentum in the Complex plane. A vector form of the energy demonstrated with the horizontal component OH=mc2, and vertical component ZH=pc |
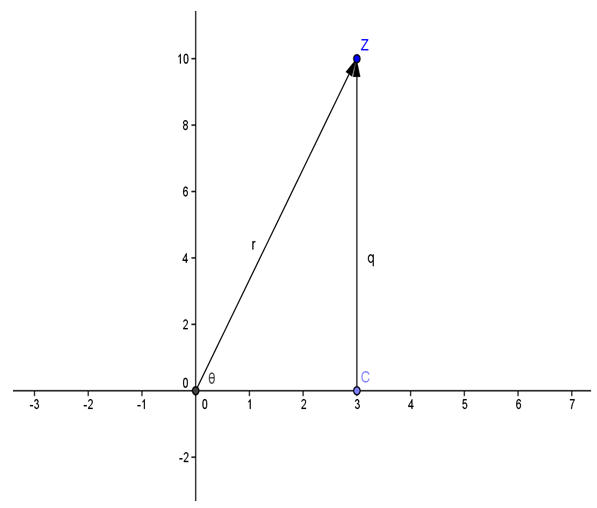 | Figure (2). The state of the Complex Matter in a complex plane with two components (m,q), where m is the real part of the "matter" and q is the imaginary part |
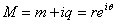 , where
, where 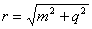 , and
, and 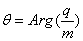 .In Fig (1), a vector form of the energy demonstrated with the horizontal component OH=mc2, and vertical component ZH=pc. Energy vector
.In Fig (1), a vector form of the energy demonstrated with the horizontal component OH=mc2, and vertical component ZH=pc. Energy vector 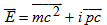 with a magnitude can be expressed by:
with a magnitude can be expressed by: 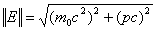 .The portraits in Fig.(1) and Fig.(2) demonstrate the implication of postulate (I) to the state of the Energy. That is, energy can be expressed with two components of real and imaginary values. The Energy of a mass-less particle can be observed on the diagram when,
.The portraits in Fig.(1) and Fig.(2) demonstrate the implication of postulate (I) to the state of the Energy. That is, energy can be expressed with two components of real and imaginary values. The Energy of a mass-less particle can be observed on the diagram when, 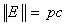 . When the real part of particle mass is not zero we will derive the energy, mass, and charge in relativistic mechanics.The complex point E can be described in the following form
. When the real part of particle mass is not zero we will derive the energy, mass, and charge in relativistic mechanics.The complex point E can be described in the following form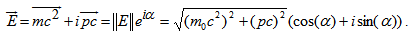 | (4.3) |
5. Derivation of Einstein's Equation in Complex Matter Space
- Using Postulate (I) let us describe a particle of a complex Matter Space by a set of points M(t)=m(t)+iq(t) where m is the mass and q is the charge at time t in the interval (a,b) for local parameters a and b. We will describe the instantaneous rate of changes of this complex matter by
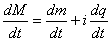 .Lemma (5.1): Given a complex matter in (4.1) then
.Lemma (5.1): Given a complex matter in (4.1) then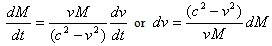 | (5.1) |

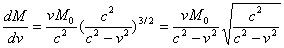

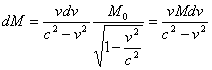 This concludes the relation (5.1).
This concludes the relation (5.1).
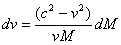 Theorem (5.1): The instantaneous rate of change in complex matter can be described by
Theorem (5.1): The instantaneous rate of change in complex matter can be described by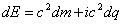 | (5.2) |
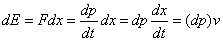 | (5.3) |
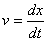 is a real vector function but the momentum
is a real vector function but the momentum 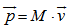 will be a complex vector function. The differentiation of momentum will be
will be a complex vector function. The differentiation of momentum will be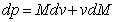 | (5.4) |

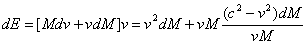 Simplifying the right hand side concludes
Simplifying the right hand side concludes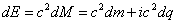 | (5.5) |

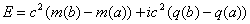 To explain the relativistic energy in Complex Matter Space, we use the trigonometric values in the complex plane;
To explain the relativistic energy in Complex Matter Space, we use the trigonometric values in the complex plane;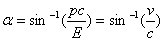 and assume
and assume 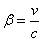

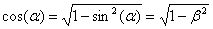 When the real part of particle mass is not zero we will derive the energy, mass, and charge in relativistic mechanics.The complex point E can be described in the following form
When the real part of particle mass is not zero we will derive the energy, mass, and charge in relativistic mechanics.The complex point E can be described in the following form
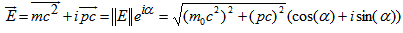 Replacing cosine and sine of angle alpha from the previous step, we will get an energy state description
Replacing cosine and sine of angle alpha from the previous step, we will get an energy state description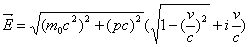 | (5.6) |

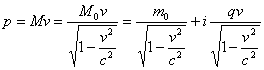
6. Relativistic View of Energy in Complex Matter Space
- I) Energy Expression: Complex Matter space will be able to interpret the duality of nature mass-wave characteristic matter. On the other hand, there are some quantum mechanical solutions that allow negative masses like the expression for relativistic energy-momentum. Let's try to re-investigate the quantum mechanical view of the SRT in Complex Matter Inner Space. This will allow us to consider mass M=m+iq. Thus, the relativistic model (1) will be in the following form:Step (1): The famous Einstein relationship for Energy-Mass for a particle will be
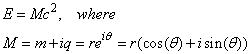 | (6.1) |
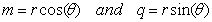 | (6.2) |

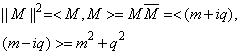 could be a best way to explain the energy and momentum computations.A free particle has a mass magnitude with Complex Matter in the Inner Space. By this property, 4.2 can be redefined by
could be a best way to explain the energy and momentum computations.A free particle has a mass magnitude with Complex Matter in the Inner Space. By this property, 4.2 can be redefined by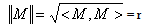 | (6.3) |
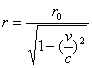 , at t=t0, for
, at t=t0, for 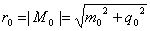 and Complex Momentum can be described by
and Complex Momentum can be described by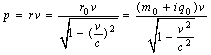 | (6.4) |

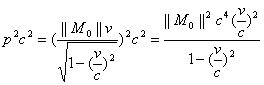

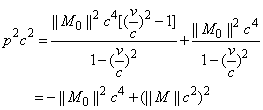 Substitute: E=||M||c2 then,
Substitute: E=||M||c2 then, 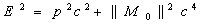 | (6.5) |
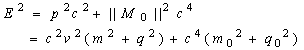 | (6.6) |

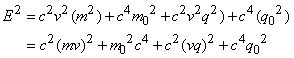

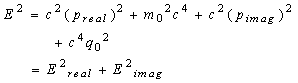 Consequently the energy in the complex plane can be described by the magnitude of a vector with two components
Consequently the energy in the complex plane can be described by the magnitude of a vector with two components 
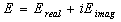
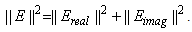 | (6.7) |
7. Discussions
- i)- Complex Matter Space, Dark Matter, and Dark Energy: If the value
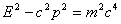 is equal to zero then we have E=pc. Since c is a constant real number then m0 =0. This is the rest mass of a photon. Indeed, that's also the reason why one can't really have a photon at rest, v=0. If the speed of a particle is c in one reference frame, it will stay c in any (non-singular) reference frame - that's another postulate of the special theory of relativity.Consider M=m+iq such that the real part mass m will satisfy the following equation. When the rest mass of a photon is zero, that is m0 =0, then the relation
is equal to zero then we have E=pc. Since c is a constant real number then m0 =0. This is the rest mass of a photon. Indeed, that's also the reason why one can't really have a photon at rest, v=0. If the speed of a particle is c in one reference frame, it will stay c in any (non-singular) reference frame - that's another postulate of the special theory of relativity.Consider M=m+iq such that the real part mass m will satisfy the following equation. When the rest mass of a photon is zero, that is m0 =0, then the relation 
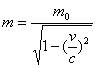 for v=c will be singular (0/0) but in a complex matter space in (4.1) for speed of a photon, v=c will not be singular.The existence of a particle traveling faster than light has been presented by many authors including, Sudarshan 1970 who discussed the Physics of complex mass.ii)-Complex Matter Space and Negative Mass: The idea of negative matter appears in past theories of matter that have now been abandoned. Using the once popular vortex theory of gravity, the possibility of matter with negative gravity was discussed by William Hicks in the 1880s.In 1928, British physicist Paul A.M. Dirac generalized Einstein's famous equation E=mc² by considering negative mass. This hypothesis allowed for the existence of anti-particles in our universeiii)- CMS explain Antiparticles: These anti-particles are, literally, mirror images of normal or real matter. Each anti-particle has the same mass as its corresponding particle, but the electrical charges are reversed. Examples of antimatter discoveries of the 20th century are: 1) Positrons - Electrons with a positive instead of negative charge, 2) Anti-protons - Protons that have a negative instead of the usual positive charge. 3) Anti-atoms - Pairing together positrons and antiprotons. Both particles involved in the interaction process are completely annihilated and create a very huge explosion that occurs when antimatter and matter interact, transferring the entire mass of both objects into energy. It is part of the dream unification theory to build a matter-antimatter reaction engine? iv)- Conclusions: The new Complex Matter postulate presented in this paper is the core foundation of this research. It was shown that with some modification it is consistent with Newtonian Mechanics. For speed less than the speed of light (v<c) similar modification demonstrates that the theory of complex matter is consistent with the Special Theory of Relativity. But for the speed faster than light then all relations and interpretations will be changed. In the complex matter space, the state of the energy and momentum and their magnitudes are presented in this paper. v)- Future Research: To validate the conclusion of the complex matter space theory by experiment is beyond the scope of this paper. The author is humbly anxious to get help from those who are capable to perform these experiments for particles with velocity close but greater than the speed of light. The states of particles and their quantum states can be studied in Complex Matter Space through interactions with other fundamental particles. The electromagnetic interaction, weak interaction forces, and strong Interaction forces can be considered. The standard model in quantum state does not consider Gravitation as part of the standard model.The Complex Matter Space theory has a potential to apply to the interactions or collisions with particles generated in variety of forces.
for v=c will be singular (0/0) but in a complex matter space in (4.1) for speed of a photon, v=c will not be singular.The existence of a particle traveling faster than light has been presented by many authors including, Sudarshan 1970 who discussed the Physics of complex mass.ii)-Complex Matter Space and Negative Mass: The idea of negative matter appears in past theories of matter that have now been abandoned. Using the once popular vortex theory of gravity, the possibility of matter with negative gravity was discussed by William Hicks in the 1880s.In 1928, British physicist Paul A.M. Dirac generalized Einstein's famous equation E=mc² by considering negative mass. This hypothesis allowed for the existence of anti-particles in our universeiii)- CMS explain Antiparticles: These anti-particles are, literally, mirror images of normal or real matter. Each anti-particle has the same mass as its corresponding particle, but the electrical charges are reversed. Examples of antimatter discoveries of the 20th century are: 1) Positrons - Electrons with a positive instead of negative charge, 2) Anti-protons - Protons that have a negative instead of the usual positive charge. 3) Anti-atoms - Pairing together positrons and antiprotons. Both particles involved in the interaction process are completely annihilated and create a very huge explosion that occurs when antimatter and matter interact, transferring the entire mass of both objects into energy. It is part of the dream unification theory to build a matter-antimatter reaction engine? iv)- Conclusions: The new Complex Matter postulate presented in this paper is the core foundation of this research. It was shown that with some modification it is consistent with Newtonian Mechanics. For speed less than the speed of light (v<c) similar modification demonstrates that the theory of complex matter is consistent with the Special Theory of Relativity. But for the speed faster than light then all relations and interpretations will be changed. In the complex matter space, the state of the energy and momentum and their magnitudes are presented in this paper. v)- Future Research: To validate the conclusion of the complex matter space theory by experiment is beyond the scope of this paper. The author is humbly anxious to get help from those who are capable to perform these experiments for particles with velocity close but greater than the speed of light. The states of particles and their quantum states can be studied in Complex Matter Space through interactions with other fundamental particles. The electromagnetic interaction, weak interaction forces, and strong Interaction forces can be considered. The standard model in quantum state does not consider Gravitation as part of the standard model.The Complex Matter Space theory has a potential to apply to the interactions or collisions with particles generated in variety of forces.  Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML