-
Paper Information
- Previous Paper
- Paper Submission
-
Journal Information
- About This Journal
- Editorial Board
- Current Issue
- Archive
- Author Guidelines
- Contact Us
Journal of Nuclear and Particle Physics
p-ISSN: 2167-6895 e-ISSN: 2167-6909
2014; 4(3): 100-115
doi:10.5923/j.jnpp.20140403.03
Mathematical Modeling for Pulsatile Flow of a Non-Newtonian Fluid with Heat and Mass Transfer in a Porous Medium between two Permeable Parallel Plates
Mohamed Y. Abou-zeid1, 2, Seham S. El-zahrani1, Hesham M. Mansour3
1Department of Mathematics, Faculty of Science, Tabuk University, Tabuk, KSA
2Department of Mathematics, Faculty of Education, Ain Shams University, Roxy, Cairo, Egypt
3Department of Physics, Faculty of Science, Cairo University Giza, Egypt
Correspondence to: Mohamed Y. Abou-zeid, Department of Mathematics, Faculty of Science, Tabuk University, Tabuk, KSA.
| Email: |  |
Copyright © 2014 Scientific & Academic Publishing. All Rights Reserved.
The aim of the present work is to investigate the effect of mixed convection heat and mass transfer on pulsatile flow of a non-Newtonian fluid which is obeying the rheological equation of state due to Ree-Eyring‘s stress-strain relation. We take into consideration the porosity of medium and a uniform magnetic field. The flow is assumed to be between two permeable vertical plates. The equations of momentum, energy and concentration have been solved by using Lightill method. The velocity, temperature and concentration distributions are obtained. The effects of various parameters of the problem on these distributions are presented and discussed.
Keywords: Pulsatile flow, Non-Newtonian fluid, Heat and mass transfer
Cite this paper: Mohamed Y. Abou-zeid, Seham S. El-zahrani, Hesham M. Mansour, Mathematical Modeling for Pulsatile Flow of a Non-Newtonian Fluid with Heat and Mass Transfer in a Porous Medium between two Permeable Parallel Plates, Journal of Nuclear and Particle Physics, Vol. 4 No. 3, 2014, pp. 100-115. doi: 10.5923/j.jnpp.20140403.03.
Article Outline
1. Introduction
- The study of pulsating flows is of practical engineering importance. High speed (turbulent) pulsating flows occur in turbo machinery, rotor blade aerodynamics, reciprocating piston-driven flows, etc. Numerous experimental investigations were focused on fundamental studies of fully developed periodic pipe flows with sinusoidal varying pressure gradients (or flow rates). Low speed (laminar) pulsating flows were studied in order to analyze the flows through small pipes or in the blood circulation systems. Laminar flows are relatively simple for analytical (or numerical) analysis and are a natural choice to provide basic studies of fundamental hydrodynamic effects in pulsating flows [1]. Pulsatile flow has also recently found renewed significance in its application to MEMS microfluidic engineering applications [2]. A complete treatment of the fluid dynamics of steady and pulsatory flow with emphasis on basic mechanics, physics and applications can be seen in Ref. [3]. Several investigations on flow through stenosed artery have been carried out to evaluate the flow characteristics under steady and pulsatile flow conditions. Young and Tsai [4-5] studied the steady and unsteady flows across a stenosis experimentally (See also Siouffi et al. [6]). In fact, blood is a complex rheological mixture showing several non-Newtonian properties, shear-thinning, yield stress, stress relaxation etc. The rheological properties of fluid have important influences on wall shear stress, oscillatory shear index etc. So it is very important to address the significance of non-Newtonian models for the purpose of reliable hemodynamic modeling [7]. Blood may be considered as a Newtonian fluid for the flow within the heart and the aorta of the human cardiovascular system. For blood flow in smaller arteries of diameter 0.5mm, a simple rescaling of the Newtonian viscosity is sufficient to take account of non-Newtonian behavior of the blood. In particular situations blood may behave as a non-Newtonian fluid, even in large arteries, as reported in Nakamura and Sawada [8]. Under diseased conditions, blood exhibits remarkable non-Newtonian properties. Eldabe et al. [9-10] studied pulsatile magneto hydrodynamic viscoelastic flow through a channel bounded by two permeable parallel plates and the effect of couple stresses on pulsatile hydro magnetic poiseuille flow.The flow through porous media has attracted considerable research activity in recent years because of its important applications notably in the flow of oil through porous rock, the extraction of energy from the geothermal regions, the evaluation of the capability of heat-removal from particulate nuclear fuel debris that may result from a hypothetical accident in a nuclear reactor, the filteration of solids from liquids, flow of ion-exchange beds, drug permeation through human skin, chemical reactors for economical separation or purification of mixtures and so on [11]. Flow through porous media is very prevalent in nature, and therefore the study of flow through a porous medium has become of principle interest in many engineering applications. Thermal and solutal transport by fluid flowing through a porous matrix is a phenomenon of great interest from the theory and application point of view. Heat transfer in the case of homogenous fluid-saturated porous media has been studied in relation to different applications like dynamic of hot underground springs, terrestrial heat flow through aquifer, hot fluid and ignition front displacements in reservoir engineering, heat exchange between soil and atmosphere and heat exchanges with fluidized beds. Mass transfer in isothermal condition has been studied with applications to problems of mixing of fresh and salt water in a quifers, spreading of solutes in fluidized beds and crystal washers, salt leaching in soils, etc. Prevention of salt dissolution into the lake waters near the sea shores has become a serious and interesting problem of research [12].Verma et al. [13] studied the pulsatile blood flow of a micro deformable fluid. A mathematical model for the study of blood flow through a channel with permeable walls of finite width is discussed by Mishra and Ghosh [14]. Vajravelu et al. [15] studied the pulsatile flow of a viscous incompressible Newtonian fluid between permeable beds. Lalit and Narayanan [16] discussed the analysis of pulsatile flow and its role on particle removal from surfaces. The pulsatile flow of blood through a mild stenosed artery under periodic body acceleration is investigated in this theoretical analysis by Mallik et. al. [17]. The problem of pulsatile flow of MHD non-Newtonian fluid obeying power law model with convective heat transfer through a non-Darcy porous medium between two coaxial cylinders is studied by Abou-zeid [18]. Shawky [19] studied the flow due to the pulsatile pressure gradient of dusty non-Newtonian fluid obeying Eyring-Powell model with heat transfer in a channel in the presence of external magnetic field.The main idea of the present work is to study the mathematical analysis of a non-Newtonian fluid flow with heat and mass transfer. The flow analysis is developed through a porous media and between two vertical permeable parallel plates, in the presence of a normal magnetic field. Analytical solutions for the momentum, energy and concentration equations have been obtained under the assumption that the pulsatile flow is a linear combination of the steady part and the oscillatory part. Also, we show the relation between the different parameters of the flow and the external forces. Numerical solutions are obtained for different values of The parameters Re , k0 , Ps , P0 , Da , M , GT , GC , Pr , Sr , Sc , ω and t.
2. Mathematical Analysis
- We consider the unsteady flow with heat and mass transfer of a viscous, incompressible, and electrically conducting non-Newtonian fluid (biviscosity fluid) in a porous medium between two permeable vertical parallel plates situated at y = 0 and y =h, under the action of the fluid gradient. The coordinates system used is shown in Fig. 1. The x- axis is taken in the direction of the flow and the y- axis is taken normal to the plates. We assume that a uniform magnetic field B0 is acting along the y- axis. The fluid is being injected into the wall through y = 0 and is being sucked through y = h with uniform velocity V0.
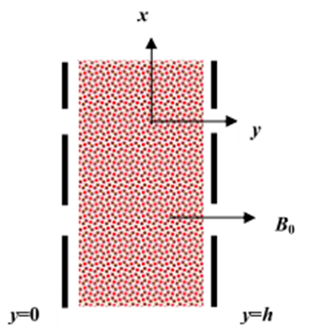 | Figure 1. The coordinate system used |
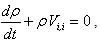 | (1) |
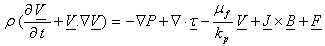 | (2) |
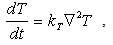 | (3) |
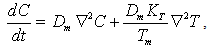 | (4) |
 The rheological equation of state for an isotropic and incompressible flow of a Ree-Eyring fluid can be written as
The rheological equation of state for an isotropic and incompressible flow of a Ree-Eyring fluid can be written as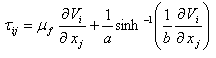 | (5) |
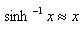 for
for  , then
, then 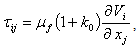 | (6) |
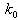 = 0.Since the two walls are infinite, all quantities are functions of y and t only. From equation (1), we get v=V0. Equations (2), (3) and (4) reduce to
= 0.Since the two walls are infinite, all quantities are functions of y and t only. From equation (1), we get v=V0. Equations (2), (3) and (4) reduce to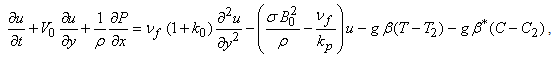 | (7) |
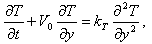 | (8) |
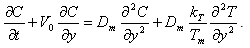 | (9) |
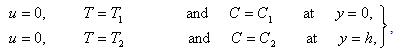 | (10) |
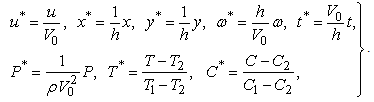 | (11) |
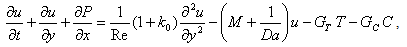 | (12) |
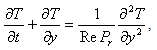 | (13) |
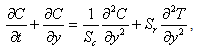 | (14) |
3. Method of Solution
- For pulsation pressure gradient, let
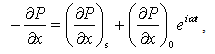 | (15) |
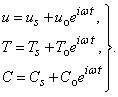 | (16) |
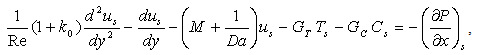 | (17) |
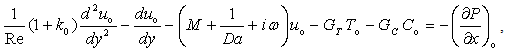 | (18) |
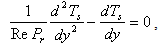 | (19) |
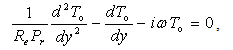 | (20) |
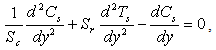 | (21) |
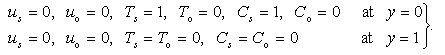 | (23) |
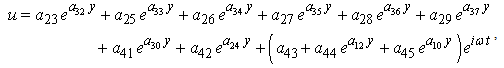 | (24) |
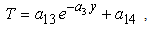 | (25) |
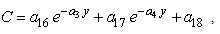 | (26) |
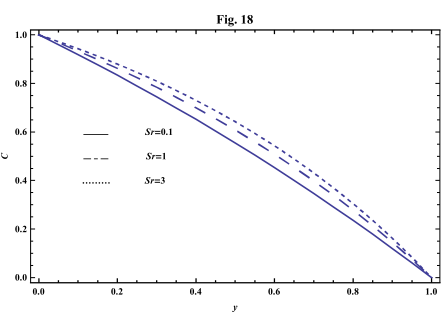
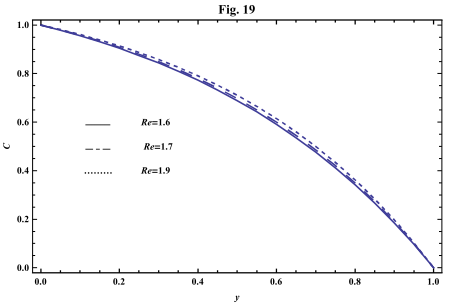
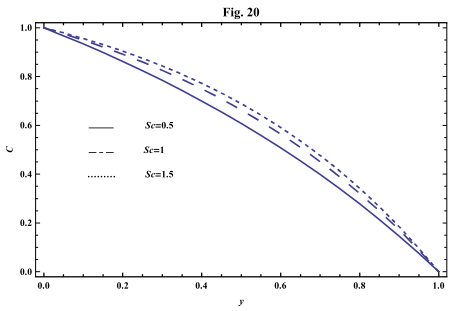
4. Numerical Results and Discussion
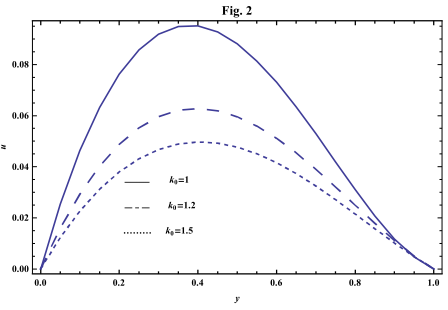
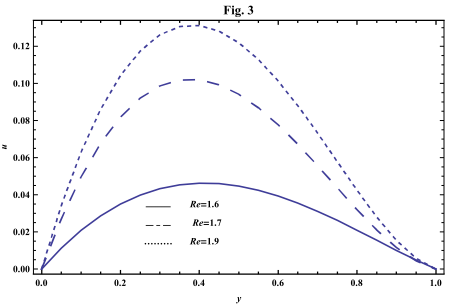
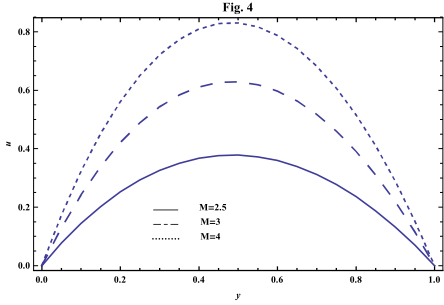
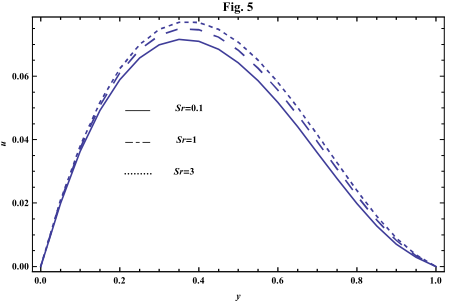
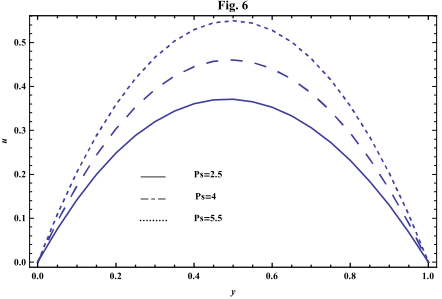
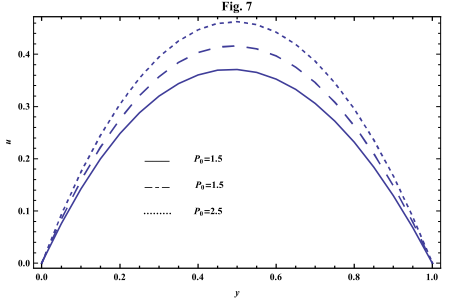
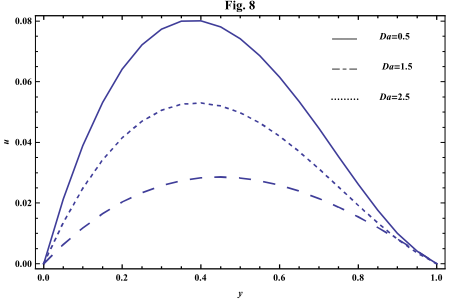
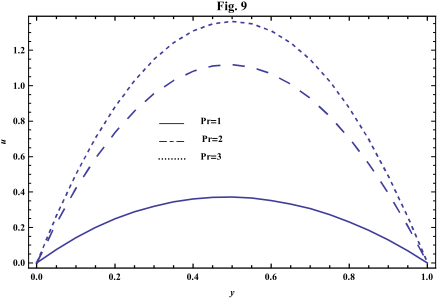
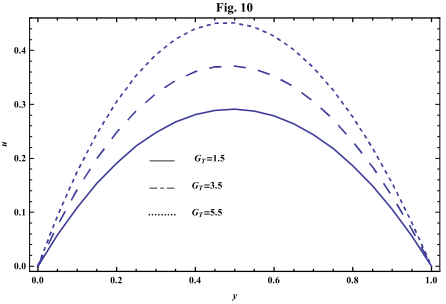
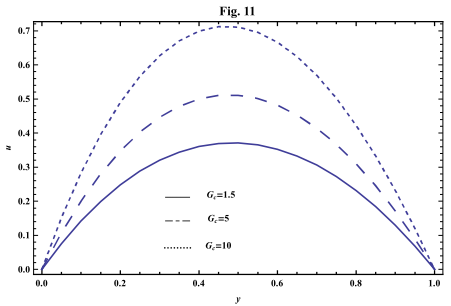
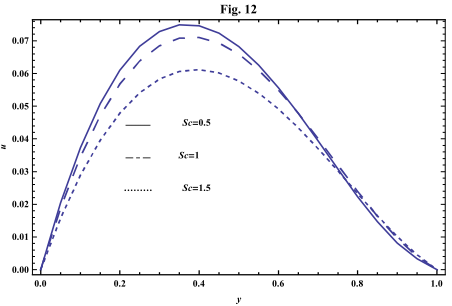
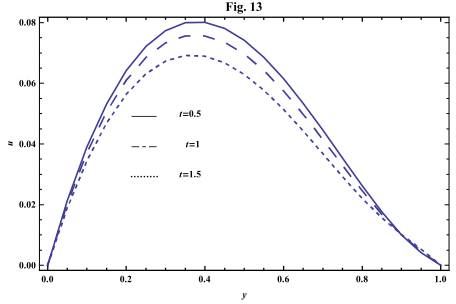
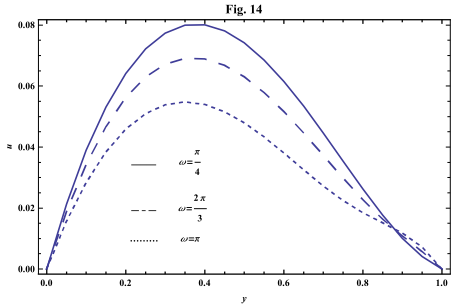
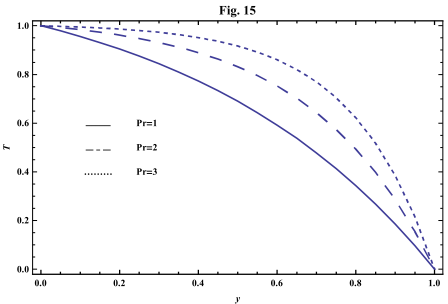
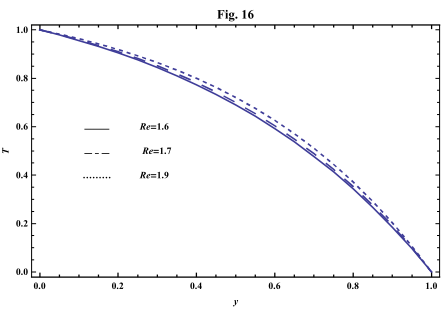
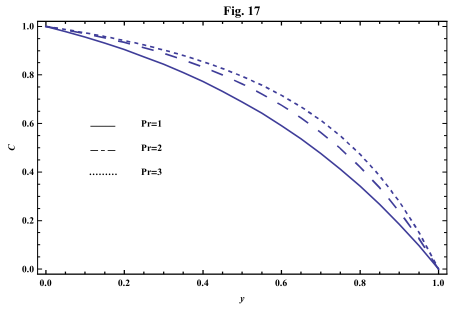
- The systems of equations that govern the non-Newtonian fluid between two vertical parallel plates are solved analytically. The formulas for velocity, temperature and concentration distributions are obtained. In order to get a physical understanding of the problem and for the purpose of discussing the results, numerical calculations have been performed to obtain the velocity, temperature and concentration. The velocity , temperature and concentration distributions are calculated for different values of Re , k0 , Ps , P0 , Da , M , GT , GC , Pr , Sr , Sc , ω and t in figures 2 - 20.
5. Conclusions
- In this paper, we have studied the problem of MHD unsteady flow with heat and mass transfer of non-Newtonian fluid which is obeying the rheological equation of state due to Ree-Eyring’s stress-strain relation. The flow is through a uniform porous medium between two vertical permeable parallel plates in the presence of convective heat and mass transfer. The equations of momentum, energy and concentration are solved analytically by using Lightill method [20]. The velocity, temperature and concentration distributions are obtained. The effects of various physical parameters of the problems on these distributions are discussed and illustrated graphically through a set of figures. Hence, this paper deals with an important branch of fluid mechanics, which has many important applications in many fields, such as biology, medicine and chemistry and also in the space science e.g.:1. The rheology of blood has received much study. Blood is rheologically complex on two counts: it is a suspension because erythrocytes with characteristic dimensions of several micrometers are present in excess of 40 % vol. and the suspension fluid itself exhibits non-Newtonian behavior because of the presence of high molecular-weight protein. The importance of rheological properties of other body fluids is now recognized. In particular, the rheological response of mucous in respiratory system of both infants and adults are an important factor for proper respiratory behavior. The lubricating action of synovial fluid in joints is likewise, strongly dependent on rheological properties [19].2. For engineering purposes, one is more interested in the values of the velocity and heat transfer than in the shape of the velocity and temperature profiles. The results of this problem are of great interest in petroleum applications such as rotating machinery, lubrication technology, viscometry, computer storage devices, food processing, biochemical operations, transport in polymers and understanding and predicting blood flow properties in large arteries. The flow of the Petroleum through the Porous ground represents a good example of the motion of our fluid especially in the motion of the fluid in the earth's core. Also, there are many applications of this motion in many fields such Astrophysical, Plasma MHD, Metallurgical processes and Geophysical applications [18].
Appendices
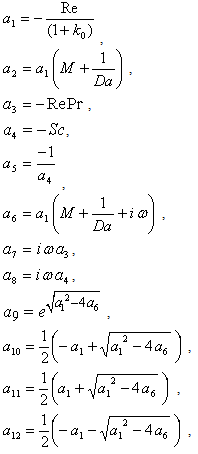

 ,
,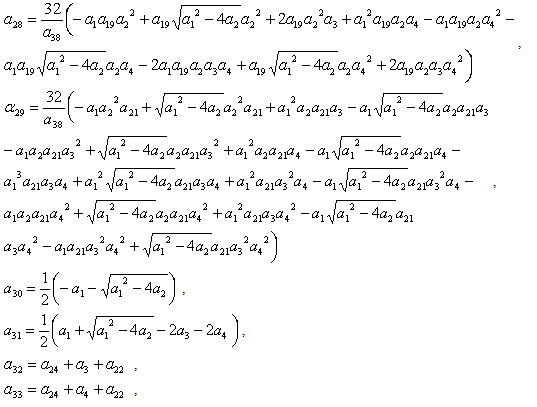 ,
,
 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML