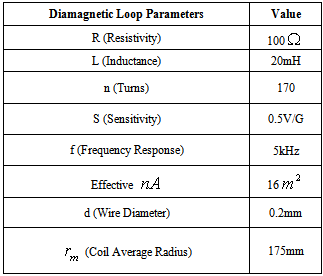
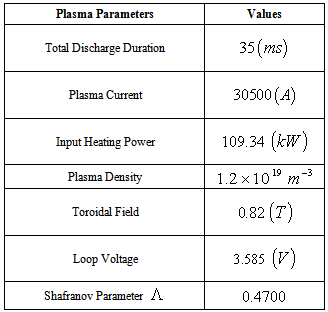
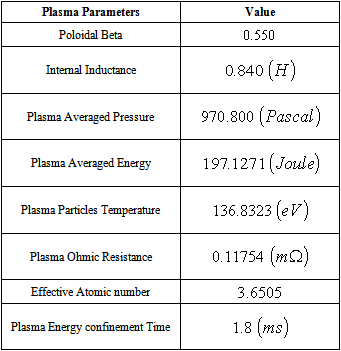
| [1] | M. Endler, Nucl. Fusion 35, 1307, (1995) |
| [2] | K. H. Burell, Phys. Plasmas 4, 1499, (1997) |
| [3] | K. H. Burell, Phys. Plasmas 6, 4418, (1999) |
| [4] | M. Spolaore et al., Czech. J. Phys. 55 (12), 1615-1621, (2005) |
| [5] | P. Devynck et al., Physics of Plasmas 13 (10), 102505-102513, (2006) |
| [6] | A. Salar Elahi et al., IEEE Trans. Plasma Science, 40, 892-897, (2012) |
| [7] | B. Viatcheslav et al., J. Plasma Fusion Res. 5, 418-423, (2002) |
| [8] | E. Y. Wang et al., Nucl. Fusion 35, 467, (1995) |
| [9] | Ch. P. Ritz et al., Rev. Sci. Instrum. 59, 1739-1744, (1998) |
| [10] | V. V. Bulanin et al., Plasma Phys. Control. Fusion 48, A101, (2006) |
| [11] | J. A. C. Cabral et al., Plasma Phys. Control. Fusion 40, 1001, (1998) |
| [12] | C. Silva et al., 17th IAEA Fusion Energy Conference, EX/P1-10 Lyon, France, (2002) |
| [13] | A. Salar Elahi et al., IEEE Trans. Plasma Science 38 (2), 181-185, (2010) |
| [14] | A. Salar Elahi et al., IEEE Trans. Plasma Science 38 (9), 3163-3167, (2010) |
| [15] | M. Emami, M. Ghoranneviss, A. Salar Elahi and A. Rahimi Rad, J. Plasma Phys. 76 (1), 1-8, (2009) |
| [16] | A. Salar Elahi et al., Fusion Engineering and Design 85, 724–727, (2010) |
| [17] | A. Salar Elahi et al., Phys. Scripta 80, 045501, (2009) |
| [18] | A. Salar Elahi et al., Phys. Scripta 80, 055502, (2009) |
| [19] | A. Salar Elahi et al., Phys. Scripta 81 (5), 055501, (2010) |
| [20] | A. Salar Elahi et al., Phys. Scripta 82, 025502, (2010) |
| [21] | M. Ghoranneviss, A. Salar Elahi et al., Phys. Scripta 82 (3), 035502, (2010) |
| [22] | A. Salar Elahi et al., J. Fusion Energy 28 (4), 346-349, (2009) |
| [23] | A. Salar Elahi et al., J. Fusion Energy 28 (4), 416-419, (2009) |
| [24] | A. Salar Elahi et al., J. Fusion Energy 28 (4), 408-411, (2009) |
| [25] | A. Salar Elahi et al., J. Fusion Energy 28 (4), 412-415, (2009) |
| [26] | A. Salar Elahi et al., J. Fusion Energy 28 (4), 394-397, (2009) |
| [27] | A. Salar Elahi et al., J. Fusion Energy 28 (4), 404-407, (2009) |
| [28] | A. Salar Elahi et al., J. Fusion Energy 28 (4), 390-393, (2009) |
| [29] | A. Salar Elahi et al., J. Fusion Energy 28 (4), 385-389, (2009) |
| [30] | A. Rahimi Rad, M. Ghoranneviss, M. Emami, and A. Salar Elahi, J. Fusion Energy 28 (4), 420-426, (2009) |
| [31] | A. Salar Elahi et al., J. Fusion Energy 29 (1), 1-4, (2010) |
| [32] | A. Salar Elahi et al., J. Fusion Energy 29 (1), 22-25, (2010) |
| [33] | A. Salar Elahi et al., J. Fusion Energy 29 (1), 29-31, (2010) |
| [34] | A. Salar Elahi et al., J. Fusion Energy 29 (1), 26-28, (2010) |
| [35] | A. Salar Elahi et al., J. Fusion Energy 29 (1), 32-35, (2010) |
| [36] | A. Salar Elahi et al., J. Fusion Energy 29 (1), 36-40, (2010) |
| [37] | A. Salar Elahi et al., J. Fusion Energy 29 (1), 62-64, (2010) |
| [38] | A. Salar Elahi et al., J. Fusion Energy 29 (1), 76-82, (2010) |
| [39] | A. Rahimi Rad, M. Emami, M. Ghoranneviss, A. Salar Elahi, J. Fusion Energy 29 (1), 73-75, (2010) |
| [40] | A. Salar Elahi et al., J. Fusion Energy 29 (1), 83-87, (2010) |
| [41] | A. Salar Elahi et al., J. Fusion Energy 29 (1), 88-93, (2010) |
| [42] | A. Salar Elahi et al., J. Fusion Energy 29 (3), 209-214, (2010) |
| [43] | A. Salar Elahi et al., J. Fusion Energy 29 (3), 232-236, (2010) |
| [44] | A. Salar Elahi et al., J. Fusion Energy 29 (3), 251-255, (2010) |
| [45] | A. Salar Elahi et al., J. Fusion Energy 29 (3), 279-284, (2010) |
| [46] | M. Ghoranneviss, A. Salar Elahi et al., J. Fusion Energy 29 (5), 467-470, (2010) |
| [47] | A. Salar Elahi et al., J. Fusion Energy 29 (5), 461-465, (2010) |
| [48] | A. Salar Elahi et al., Brazilian J. Physics 40 (3), 323-326, (2010). |
| [49] | A. Salar Elahi et al., J. Fusion Energy 30 (2), 116-120, (2011) |
| [50] | M.R. Ghanbari, M. Ghoranneviss, A. Salar Elahi et al., Phys. Scripta 83, 055501, (2011) |
| [51] | A. Salar Elahi, J. Fusion Energy 30 (6), 477-480, 477-480, (2011) |
| [52] | A. Salar Elahi et al., Fusion Engineering and Design 86, 442–445, (2011) |
| [53] | A. Salar Elahi et al., J. Fusion Energy 31 (2), 191-194, (2012) |
| [54] | M.R. Ghanbari, M. Ghoranneviss, A. Salar Elahi and S. Mohammadi, Radiation Effects & Defects in Solids 166 (10), 789–794, (2011) |
| [55] | A. Salar Elahi et al., IEEE Trans. Plasma Science (January 2013, in press), DOI: 10.1109/TPS.2012.2235186 |
| [56] | A. Salar Elahi et al., Accepted for publication in Radiation Effects & Defects in Solids (January 2012, in press), DOI: 10.1080/10420150.2011.650171 |
| [57] | Z. Goodarzi, M. Ghoranneviss and A. Salar Elahi, Accepted for the publication in J. Fusion Energy (March 2012, in press), DOI: 10.1007/s10894-012-9526-4 |
| [58] | M.R. Ghanbari, M. Ghoranneviss, A. Salar Elahi et al., Phys. Scripta 85 (5), 055502, (2012) |
| [59] | A. Salar Elahi et al., Accepted for the publication in Radiation Effects and Defects in Solids (June 2012, in press), DOI: 10.1080/10420150.2012.706609 |
| [60] | A. Salar Elahi et al., Accepted for the publication in Radiation Effects and Defects in Solids (June 2012, in press), DOI: 10.1080/10420150.2012.706607 |
| [61] | K. Mikaili Agah, M. Ghoranneviss, A. Salar Elahi et al., accepted for the publication in J. Fusion Energy (July 2012, in press), DOI: 10.1007/s10894-012-9563-z |
| [62] | A. Salar Elahi et al., J. Nuclear and Particle Physics 1(1), (2011), 10-15, DOI: 10.5923/j.jnpp.20110101.03 |
| [63] | A. Salar Elahi et al., J. Nuclear and Particle Physics 2(2), (2012), 1-5, DOI: 10.5923/j.jnpp.20120202.01 |
| [64] | A. Salar Elahi et al., Fusion Engineering and Design (January 2013, in press), DOI: 10.1016/j.fusengdes.2012.12.001 |
| [65] | A. Salar Elahi et al., J. Nuclear and Particle Physics 2(2), 22-25, (2012), DOI: DOI: 10.5923/j.jnpp.20120202.05 |
| [66] | A. Salar Elahi et al., J. Nuclear and Particle Physics 2(5), 112-118, (2012), DOI: 10.5923/j.jnpp.20120205.02 |
| [67] | A. Salar Elahi et al., J. Nuclear and Particle Physics 2(6), 142-146, (2012), DOI: 10.5923/j.jnpp.20120206.02 |

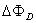 produced by the circular plasma. The relation between the diamagnetic flux and the poloidal beta derived from simplified equilibrium relation is [1-3]:
produced by the circular plasma. The relation between the diamagnetic flux and the poloidal beta derived from simplified equilibrium relation is [1-3]: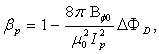
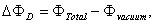 and
and 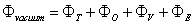 , and where
, and where 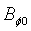 is the toroidal magnetic field in the absence of the plasma which can be obtained by the magnetic probe,
is the toroidal magnetic field in the absence of the plasma which can be obtained by the magnetic probe, 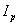 is the plasma current which can be obtained by the rogowski coil,
is the plasma current which can be obtained by the rogowski coil, 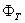 is the toroidal flux because of toroidal field coils,
is the toroidal flux because of toroidal field coils, 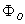 and
and 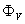 are the passing flux through loop due to possible misalignment between ohmic field and vertical field and the diamagnetic loop and
are the passing flux through loop due to possible misalignment between ohmic field and vertical field and the diamagnetic loop and 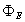 is the toroidal field due to eddy current on the vacuum chamber. These fluxes can be compensated either with compensation coil or dry runs technique (fields discharge only shots i.e. no plasma shots). It must be noted that compensating coil for diamagnetic loop is wrapped out of the plasma current, and only the toroidal flux (which is induced by the change of toroidal field coil current when plasma discharges) can be received. As seen in Eq. (1) the diamagnetic loop signal contains two parts, plasma diamagnetic flux and the vacuum toroidal flux. So the diamagnetic flux
is the toroidal field due to eddy current on the vacuum chamber. These fluxes can be compensated either with compensation coil or dry runs technique (fields discharge only shots i.e. no plasma shots). It must be noted that compensating coil for diamagnetic loop is wrapped out of the plasma current, and only the toroidal flux (which is induced by the change of toroidal field coil current when plasma discharges) can be received. As seen in Eq. (1) the diamagnetic loop signal contains two parts, plasma diamagnetic flux and the vacuum toroidal flux. So the diamagnetic flux 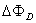 caused by plasma current can be measured from the diamagnetic loop and compensating coil using subtraction. If we want to have a determination of the volume averaged plasma kinetic pressure
caused by plasma current can be measured from the diamagnetic loop and compensating coil using subtraction. If we want to have a determination of the volume averaged plasma kinetic pressure 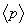 , it is can be measured directly from the definition of the poloidal beta:
, it is can be measured directly from the definition of the poloidal beta: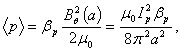
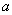 is the plasma minor radius.For measurement of the plasma thermal energy we start from the plasma state equation:
is the plasma minor radius.For measurement of the plasma thermal energy we start from the plasma state equation: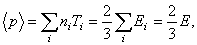
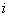 indicate the plasma species
indicate the plasma species 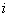 , and
, and 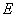 indicate the plasma thermal energy density, therefore the plasma thermal energy
indicate the plasma thermal energy density, therefore the plasma thermal energy 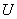 , is obtained:
, is obtained: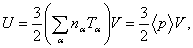
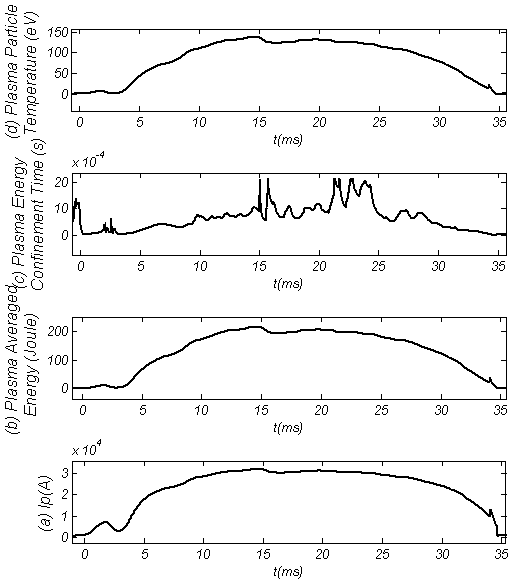
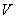 is the plasma volume. Therefore according to above discussion we can find the poloidal beta and the plasma thermal energy by the diamagnetic loop. Experimental results for determinations of these parameters will be presented in the next section.
is the plasma volume. Therefore according to above discussion we can find the poloidal beta and the plasma thermal energy by the diamagnetic loop. Experimental results for determinations of these parameters will be presented in the next section. 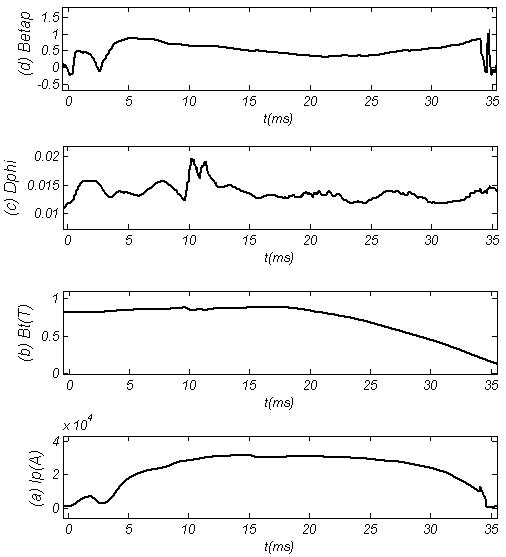
 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML