-
Paper Information
- Previous Paper
- Paper Submission
-
Journal Information
- About This Journal
- Editorial Board
- Current Issue
- Archive
- Author Guidelines
- Contact Us
Journal of Nuclear and Particle Physics
p-ISSN: 2167-6895 e-ISSN: 2167-6909
2013; 3(4): 77-96
doi:10.5923/j.jnpp.20130304.05
The Hot and Cold Properties of Nuclear Matter
Khaled Hassaneen1, 2, Hesham Mansour3
1Department of Physics, Faculty of Science, Sohag University, Sohag, Egypt
2Department of Physics, Faculty of Science, Taif University, Taif, Saudi Arabia
3Department of Physics, Faculty of Science, Cairo University, Gizza, Egypt
Correspondence to: Khaled Hassaneen, Department of Physics, Faculty of Science, Sohag University, Sohag, Egypt.
| Email: |  |
Copyright © 2012 Scientific & Academic Publishing. All Rights Reserved.
The properties of nuclear matter at zero and finite temperatures in the frame of the Brueckner theory realistic nucleon-nucleon potentials are studied. Comparison with other calculations is made. In addition we present results for the symmetry energy obtained with different potentials, which is of great importance in astrophysical calculation. Properties of asymmetric nuclear matter are derived from various many-body approaches. This includes phenomenological ones like the Skyrme Hartree-Fock and relativistic mean field approaches, which are adjusted to fit properties of nuclei, as well as more microscopic attempts like the BHF approximation, a Self-Consistent Greens Function (SCGF) method and the so-called Vlowk approach, which are based on realistic nucleon-nucleon interactions which reproduce the nucleon-nucleon phase shifts. These microscopic approaches are supplemented by a density-dependent contact interaction to achieve the empirical saturation property of symmetric nuclear matter. Special attention is paid to behavior of the isovector and the isoscalar component of the effective mass in neutron-rich matter. The nuclear symmetry potential at fixed nuclear density is also calculated and its value decreases with increasing the nucleon energy. In particular, the nuclear symmetry potential at saturation density changes from positive to negative values at nucleon kinetic energy of about 200 MeV. The hot properties of nuclear matter are also calculated using T2–approximation method at low temperatures. Good agreement is obtained in comparison with previous theoretical estimates and experimental data especially at low densities.
Keywords: Brueckner-Hartree-Fock Approximation, Self-Consistent Greens Function (SCGF) Method, Three-body Forces, Symmetry Energy, Symmetry Potential, Effective Mass, T2–approximation Method
Cite this paper: Khaled Hassaneen, Hesham Mansour, The Hot and Cold Properties of Nuclear Matter, Journal of Nuclear and Particle Physics, Vol. 3 No. 4, 2013, pp. 77-96. doi: 10.5923/j.jnpp.20130304.05.
Article Outline
1. Introduction
- One of the most fundamental problems in nuclear many-body theory is the attempt to evaluate the nuclear matter binding energy and saturation properties, starting from a realistic Nucleon-Nucleon (NN) interaction with no free parameters. In fact a lot of work has been done trying to solve this problem using different approaches and methods which are discussed in details by Müther and Polls[1]. An important ingredient of all these approaches is the consideration of the two-nucleon correlations which are induced by the strong short-range components of the NN interaction. In lowest-order Brueckner theory, the familiar Brueckner-Hartree-Fock (BHF) approach, is adopted to calculate the energy, the so-called G-matrix for evaluating the energy in the Hartree-Fock approach. In the G-matrix one accounts for the particle-particle correlations which means the scattering of two nucleons from states which are occupied in the Slatter determinant describing the ground state, into unoccupied particle states above the Fermi surface[2-4].The potentials we will employ here are the recent models of the Nijmegen group[5], the Argonne V18 potential[6] and the charge-dependent Bonn potential (CD-Bonn)[7]. The recent versions of The Nijmegen group are Nijm-I, Nijm-II and Reid93 potentials. Although all these potentials predict almost identical phase shifts, their mathematical structure is quite different.Most of the microscopic calculations have been addressed to study symmetric matter[2] and pure neutron matter[8,9]. The study of asymmetric nuclear matter is technically more involved and only few Brueckner-Hartree-Fock (BHF) calculations are available[4,10,11]. The BHF approximation includes the self-consistent procedure of determining the single-particle auxiliary potential, as first devised by Brueckner and Gammel[12], which is an essential ingredient of the method. Different approaches have been used to study the EoS of asymmetric nuclear matter including Dirac-Brueckner-Hartree-Fock (DBHF) calculations[13-16], Brueckner-Hartree-Fock (BHF) approximation to Brueckner-Bethe-Goldstone (BBG) calculations[17,18] and variational methods[19,20]. Besides these microscopic approaches, effective theories such as Relativistic Mean Field (RMF) theory[21,22] and non-relativistic effective interactions[23,24] have also been used extensively to study the EoS and mean field properties of the asymmetric nuclear matter.As it is well known, the BHF approximation largely violates the Hugenholtz-Van Hove (HVH) theorem[26], which basically measures the consistency of a given order of approximation in a perturbative approach. In symmetric nuclear matter, the inclusion of the so-called hole-hole (hh) contribution greatly improves the fulfillment of the HVH theorem[27]. We use realistic NN forces and operate within SCGF framework. It is well known that the selfconsistent BHF approach does not reproduce the correct saturation point of nuclear matter with only the inclusion of the two-body interaction[28,29]. But our attention is mainly focused on how nuclear matter properties change in terms of the asymmetry ratio and some caution has to be taken whenever saturation properties are involved. In addition, it gives a simple microscopic justification of the empirical laws governing asymmetric nuclear matter.
1.1. In the Present Report
- In order to establish the importance of the hh term in the calculation of EoS for asymmetric nuclear matter our aim is to extend the BHF approach which ignores the hh term to SCGF approach, which includes the hh term. It has been shown, in the case of pure neutron matter[30] and also symmetric nuclear matter[2,30] that the new terms give a large contribution to single-particle properties like the mean field and the nucleon effective mass. We will refer to the present approach to compute nuclear single-particle properties as SCGF approximation[2,4].The nuclear matter symmetry energy, which is defined as the difference in energy per nucleon between the pure neutron matter and the symmetric nuclear matter, is an important quantity that determines the properties of objects such as the atomic nucleus and the neutron star[31]. The study of symmetry energy and its dependence on nuclear density and temperature is currently a subject of great interest[32]. Theoretically, the symmetry energy can be determined from microscopic calculations such as the Self-Consistent Green Function (SCGF) and theDirac-Brueckner-Hartree-Fock (DBHF) calculations, or the phenomenological calculations such as the Skyrme Hartree-Fock (SHF) and the Relativistic Mean Field (RMF) calculations[4, 31, 33-35]. These calculations currently predict wide range of symmetry energies for densities below and above normal nuclear density, ρ0 = 0.16fm3. Also, the symmetry energy and its relation with the chemical potential have been studied.Also, the properties of asymmetric nuclear matter are derived from various many-body approaches. This includes phenomenological ones like the Skyrme Hartree-Fock and relativistic mean field approaches, which are adjusted to fit properties of nuclei, as well as more microscopic attempts like the Brueckner-Hartree-Fock approximation, a self-consistent Greens function method and the so-called Vlowk approach. These microscopic approaches are supplemented by a density-dependent contact interaction to achieve the empirical saturation property of symmetric nuclear matter. The predictions of the isovector component of the effective mass in neutron-rich matter, the symmetry potential and symmetry energy are discussed.The one-body potentials for protons and neutrons are obtained from the self-consistent Green-function calculations of asymmetric nuclear matter, in particular their dependence on the degree of proton/neutron asymmetry. Results of the binding energy per nucleon as a function of the density and asymmetry parameter are presented for the self-consistent Green function approach using the CD-Bonn potential. The nuclear symmetry potential at fixed nuclear density is also calculated and its value decreases with increasing the nucleon energy. The isoscalar proton/neutron effective mass splitting in neutron-rich matter has been studied.Recently, Li et al.[36] have studied the saturation properties of nuclear matter within the Brueckner-Hartree-Fock approach using continuous single particle energies and employing the most recent accurate nucleon-nucleon potentials. They found that their results confirm the concept of “Coester line“ or “Coester band“, i.e., density and energy of the various saturation points being strongly correlated, yielding either a too large saturation density or a too small binding energy.The many-body method we will employ in deriving the EoS of both symmetric and pure nuclear matter is a rather simple one i.e., the non-relativistic BHF method with a conventional and continuous single particle spectrum using different modern NN potentials.The results in the present work which come out by approximating the single particle self-consistent potential with a parabolic form.
1.2. The Theoretical Model
1.2.1. Brueckner-Hartree-Fock for Symmetric Nuclear Matter
- In the BHF approximation, the nuclear matter total energy EA is obtained from the Brueckner G-matrix, G(ω), according to the equation:
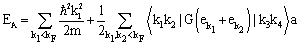 | (1) |
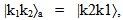 i.e., the subscript a indicates antisymmetrization of the matrix elements. Here kF is the Fermi momentum, the summation over the momenta ki include spin and isospin variables. The single particle energies ek, appearing in the entry energy of the G-matrix, are given by:
i.e., the subscript a indicates antisymmetrization of the matrix elements. Here kF is the Fermi momentum, the summation over the momenta ki include spin and isospin variables. The single particle energies ek, appearing in the entry energy of the G-matrix, are given by: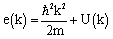 | (2) |
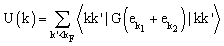 | (3) |
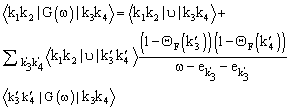 | (4) |
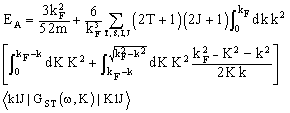 | (5) |
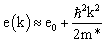 | (6) |
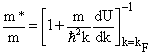 | (7) |
1.3. Brueckner-Hartree-Fock for Asymmetric Nuclear Matter
- The self-energy of a nucleon with isospin i, momentum k and energy ω in asymmetric nuclear matter is defined in the BHF approximation by[1, 4],
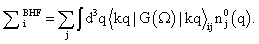 | (8) |
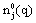 refers to the occupation probability of a free Fermi gas of protons (j = p) and neutrons (j = n) like in the mean-field or Hartree-Fock approach. This means that for asymmetric matter with a total density ρ = ρp+ρn this probability is defined by:
refers to the occupation probability of a free Fermi gas of protons (j = p) and neutrons (j = n) like in the mean-field or Hartree-Fock approach. This means that for asymmetric matter with a total density ρ = ρp+ρn this probability is defined by: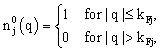 | (9) |
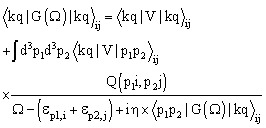 | (10) |
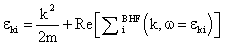 | (11) |
1.4. Self-Consistent Green’s Function
- One of the drawbacks of the BHF approximation is the fact that it does not provide results for the equation of state, which are consistent from the point of view of thermodynamics. As an example we mention that BHF results do not fulfill e.g., the Hugenholtz van Hove theorem. This is due to the fact that the BHF approximation does not consider the propagation of particle and hole states on equal footing. An extension of the BHF approximation, which obeys this symmetry is the Self-Consistent Green’s Function (SCGF) method. During the last years techniques have been developed, which allow to evaluate the solution of the SCGF equations for microscopic NN interactions. Those calculation demonstrate that for the case of realistic NN interactions, the contribution of particle-particle ladders dominates the contribution of corresponding hole-hole propagation terms. This justifies the use of the BHF approximation and a procedure, which goes beyond BHF and accounts for hole-hole terms in a perturbative way[2, 39]. This leads to a modification of the self-energy in the BHF approximation by adding a hole-hole term of the form:
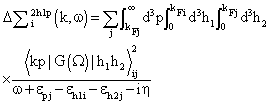 | (12) |
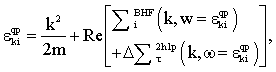 | (13) |
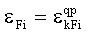 | (14) |
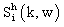 and
and 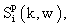 are obtained from the real and imaginary part of the self-energy
are obtained from the real and imaginary part of the self-energy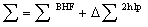 :
: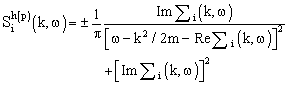 | (15) |
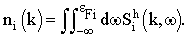 | (16) |
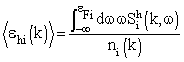 | (17) |
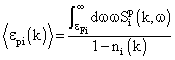 | (18) |
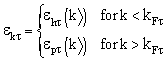 | (19) |
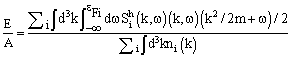 | (20) |
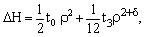 | (21) |
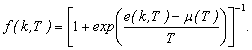 | (22) |
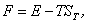 | (23) |
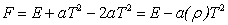 | (24) |
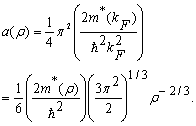 | (25) |
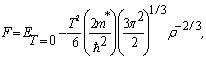 | (26) |
2. Results and Discussion
2.1. The Symmetric and Pure Neutron Matter
2.1.1. The Single Particle Energy
- In this section we present the results for the single particle energies which is calculating using Equation (2). More discussion can be read in[46]. Figure 1 shows the dependence of the single particle energy on the momentum k up to kfit = 1.6kF for symmetric nuclear matter using the CD-Bonn potential (solid curve), the Argonne V18 potential (dashed-double dot curve), the Nijm-I potential (dotted curve), the Nijm-II potential (dashed curve) and the Reid 93 potential (dashed-dot curve) at the normal saturation density ρ0 = 0.16 fm3 in terms of Fermi momentum, kF =1.333 fm1. Left panel for conventional choice, right panel for continuous choice. We observe that the results of all potentials are close to each other in the conventional choice and at high momentum after k = kF the results of all potentials come together, this means that the effect of the potential disappear at values above Fermi momentum kF. In the continuous choice we note that the CD-Bonn and Nijm-I (non-local) potentials are more attractive than the Argonne V18, the Nijm-II and the Reid 93 (local) potentials and the difference between the potentials continues even at high momentum k, this means that the effect of the potential continues at values above kF.If we compare the results we note that, one finds that the single particle energies are more attractive in the continuous choice than those in the conventional choice.
2.2. The Nuclear Matter Binding Energy
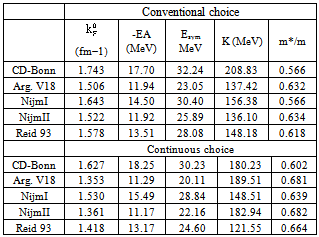
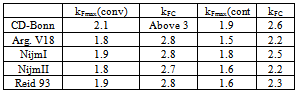
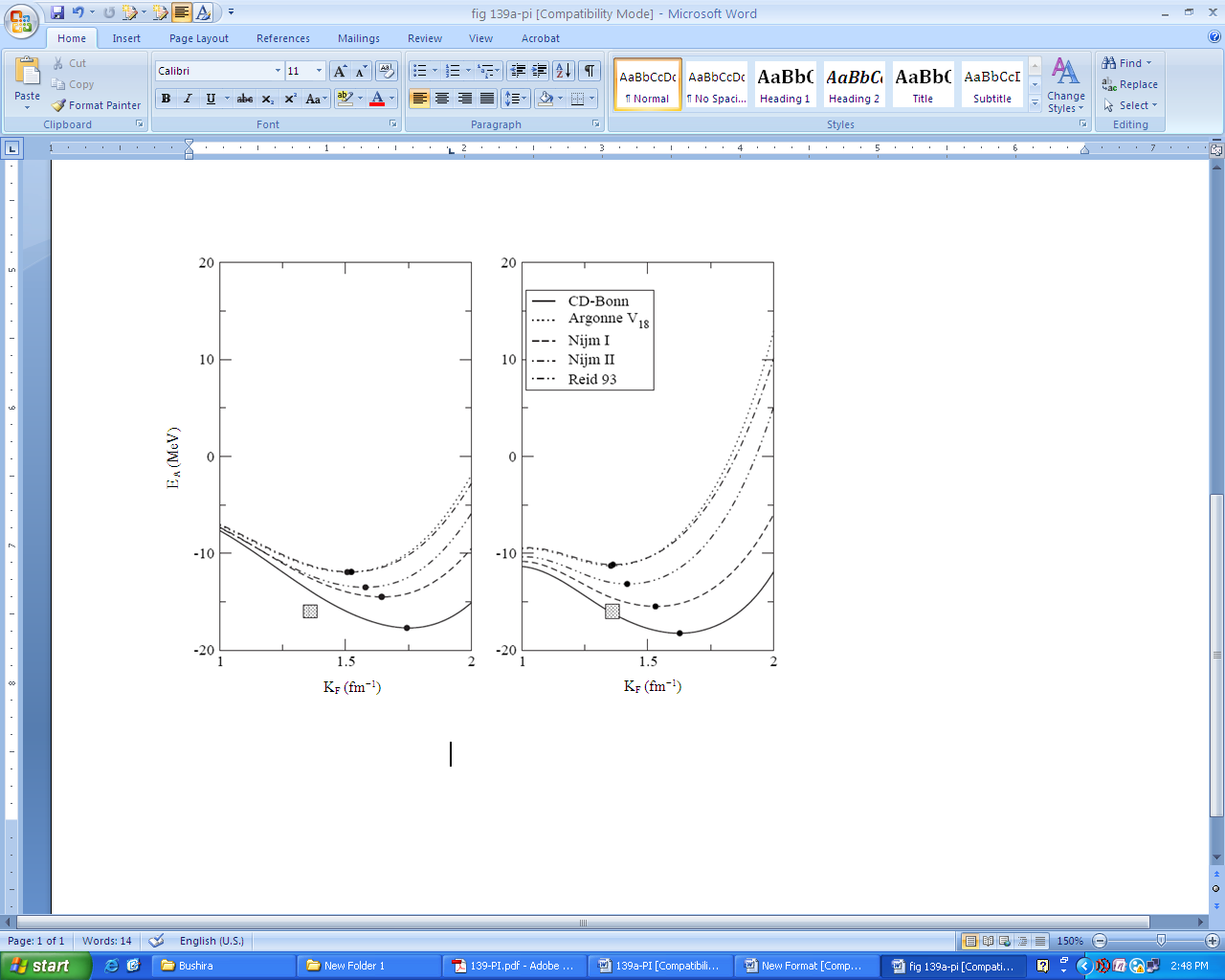
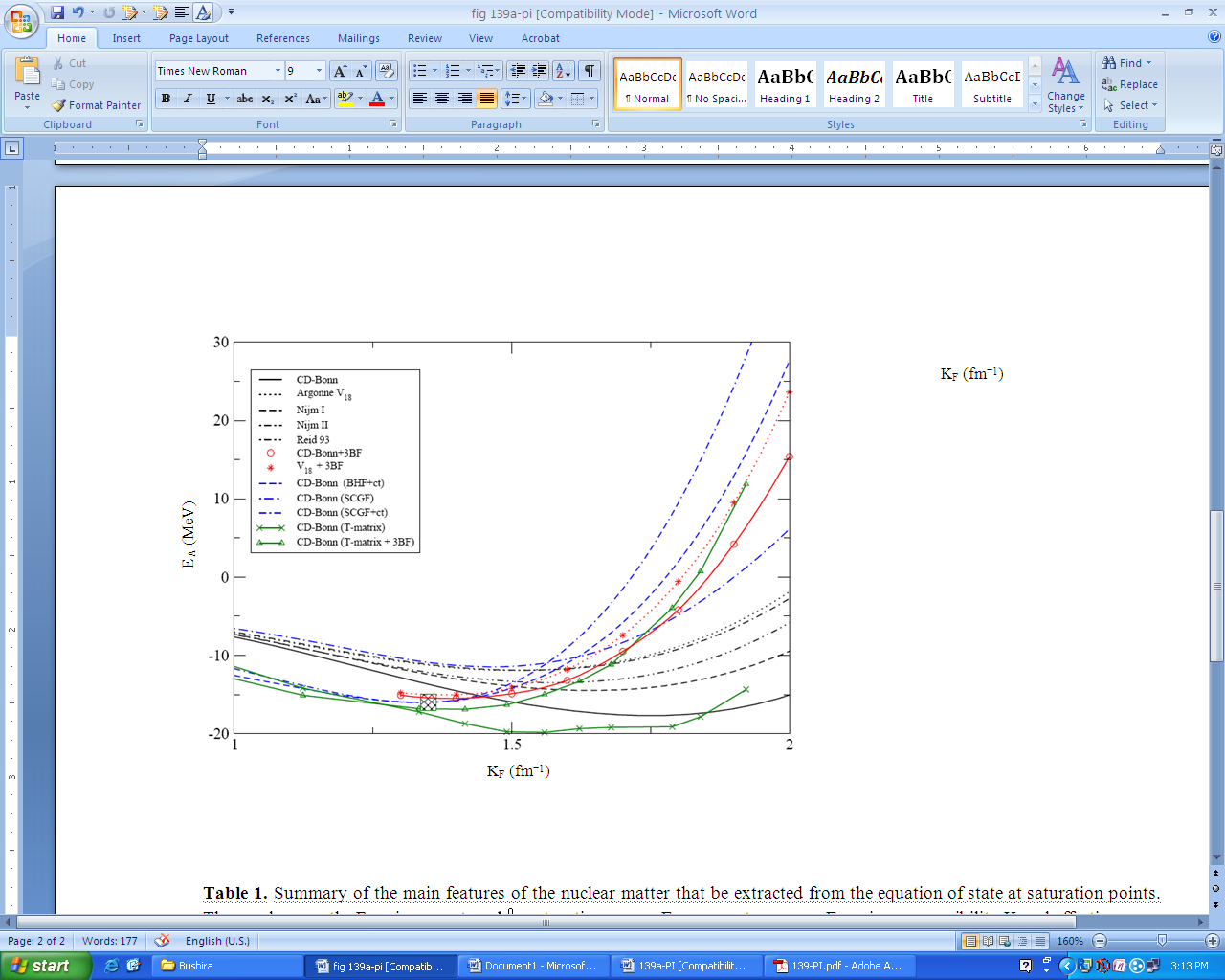
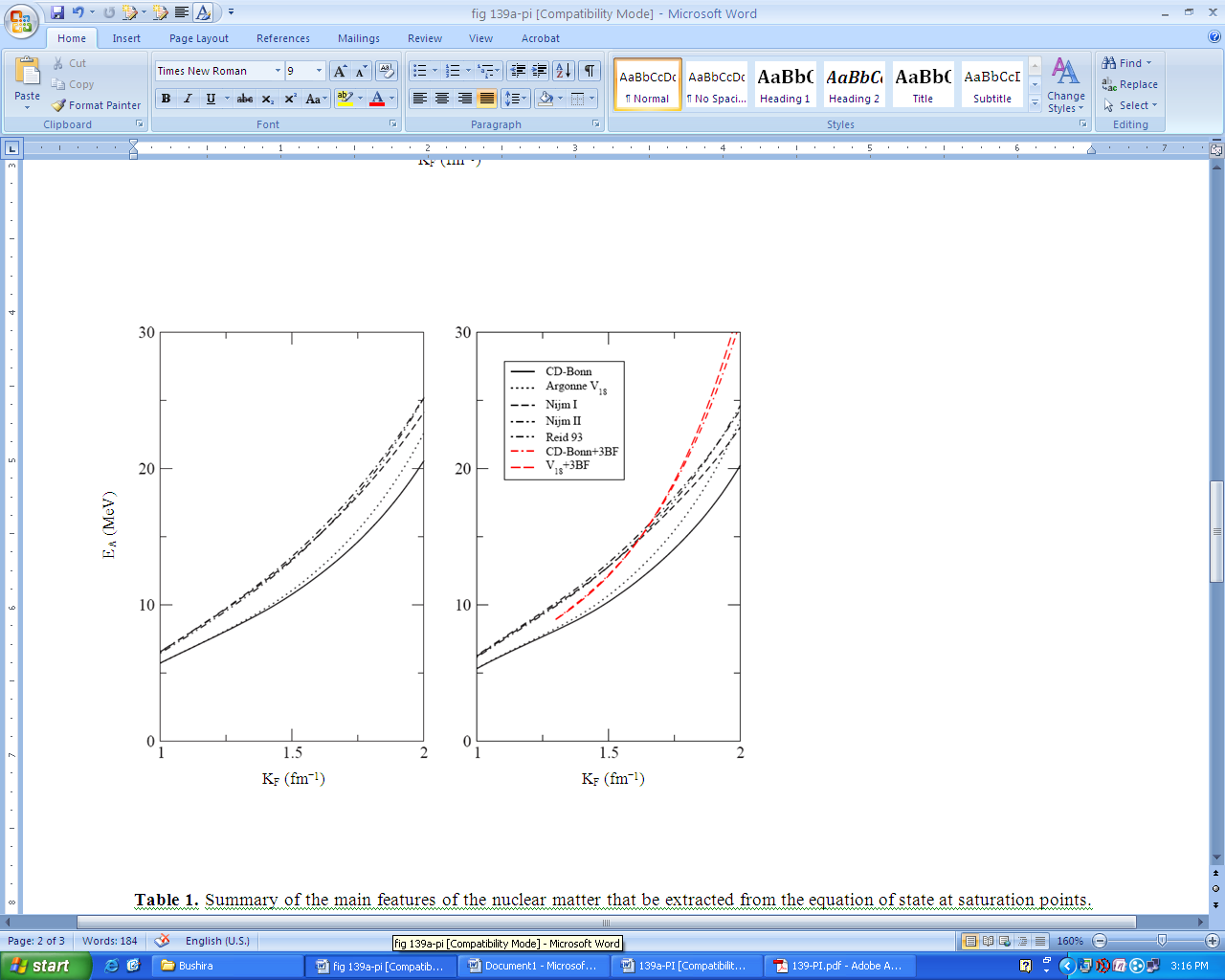
- We present the results of the non-relativistic BHF calculations in Fig. 2 obtained with different modern NN potentials. The energy per particle EA in MeV is plotted against the density ρ in terms of Fermi momentum kF in fm1, for symmetric nuclear matter using different potentials, the CD-Bonn potential (solid line), the three Nijmegen potentials, Nijm-I (short dashes), Nijm-II (double dot-dashed line) and Reid 93 (dot-dashed line) and the Argonne V18 potential (dotted line). Left panel is for conventional choice and the right panel is for continuous choice. The solid points indicate the saturation points and the dashed box indicates the empirical saturation one. One observes from the figure that the binding energy per nucleon, first decreases with increasing kF, until it reaches the minimum (saturation) point then it increases with increasing the Fermi momentum kF. The continuous choice leads to an enhancement of correlation effects in the medium and tends to predict larger binding energies for nuclear matter than the conventional choice.It is found that our calculations lead to results for saturation points, which lie along a line (Coester line) shifted with respect to the phenomenological saturation point (ρ0 = 0.16 fm3; EA = -16MeV). One can see that the continuous choice leads to an enhancement of correlation effects in the medium and tends to predict larger binding energies for nuclear matter than the conventional choice. In the continuous choice that line is close to the empirical data than the conventional choice. So, we can say that our results confirm the concept of a “line”, density and energy of the various saturation points being strongly linearly correlated, where that be consistent with the results in Refs.[36, 48]. The saturation points for our results are presented in Table 1.A very important source for the origin of the two-body correlations is the tensor force, which for example, describes the scattering of a proton-neutron pair, which originally is in a relative 3S1 state with momentum below kF, into a 3D1 state above the Fermi sea. A measure of the strength of the tensor force is expressed in term of the D-state probability PD obtained for the deuteron[48, 49]. We also observe from Table 1 that the continuous choice in the Nijm-II potential and Argonne V18 potential obey approximately the correct Fermi momentum saturation point but at low binding energy per nucleon. The continuous choice in the Nijm-I potential obeys approximately the correct binding energy per nucleon but at high Fermi momentum. The CD-Bonn potential leads to strong over-binding and too high saturation density than the others, because it contains a weak tensor force. It looks that any increase of the non-locality would improve the fitting of binding energy of nuclear matter, but shifts the saturation point to higher density and binding energy.In Fig. 3, we plot, for comparison also, the energy per particle as a function of Fermi momentum kF using the continuous choice for the single particle auxiliary potential with the results obtained with the T-matrix and T-matrix +3BF method with CD-Bonn potential by Somua and Bozek[50] and with BHF +3BF using both CD-Bonn and Argonne V18 potentials by Baldo and Shaban[51]. There is another method can be used to enhance the present results if one goes beyond BHF approach.In Fig. 4, the energy per particle EA is plotted against Fermi momentum kF, for pure neutron matter using different potentials. Left panel is for conventional choice, right panel is for continuous choice. We compare the results by CD-Bonn +3BF and V18+3BF. The pure neutron matter EoS is unbound with the energy per nucleon rising approximately monotonically with increasing the Fermi momentum, which is in agreement with most of the many-body calculations. We note that the differences between the potentials are small, because the main source of differences among the potentials is in the strength of the tensor force, which is mostly reflected in the (T = 0) 3S1-3D1 coupled states. In pure neutron matter (T = 1), however, this partial wave does not contribute.Only T=1 states contribute to the energy of pure neutron matter while both isospin states contribute to the energy of symmetric nuclear matter, if major T = 0 partial waves become increasingly repulsive at short distances. It is possible for the energy of symmetric nuclear matter to grow at a faster rate and eventually approach the neutron matter EoS. This is just what we observe in our model. In the presence of repulsive forces only, symmetric matter would be a more repulsive system than neutron matter (for the same kF).
2.3. Symmetry Energy
- The neutron matter EoS combined with that of symmetric nuclear matter provides us with information on the isospin effects[10], in particular on the symmetry energy.The energy per nucleon for nuclear matter is a function of the density ρ and the asymmetry parameter α .Hence, using Taylor's expansion and ignoring higher order terms:
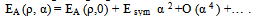 | (27) |
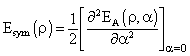 | (28) |
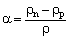 | (29) |
2.4. Asymmetric Nuclear Matter
2.4.1. The Binding Energy
- Figure 6 shows the energy per nucleon as a function of the density ρ in asymmetric nuclear matter for various values of the asymmetry parameter a. In order to establish the importance of the hole-hole term in the calculated binding energy we have compared BHF calculations (which ignore the hole-hole term) with SCGF, which includes the hole-hole term. As expected, the hh term gives a repulsive contribution to the EoS of asymmetric nuclear matter. This contribution becomes stronger by increasing the density and makes the EoS at high density much stiffer. As the density increases the phase space for the hole-hole propagator is no longer negligible, resulting in an enhanced repulsive effect on the total energy.
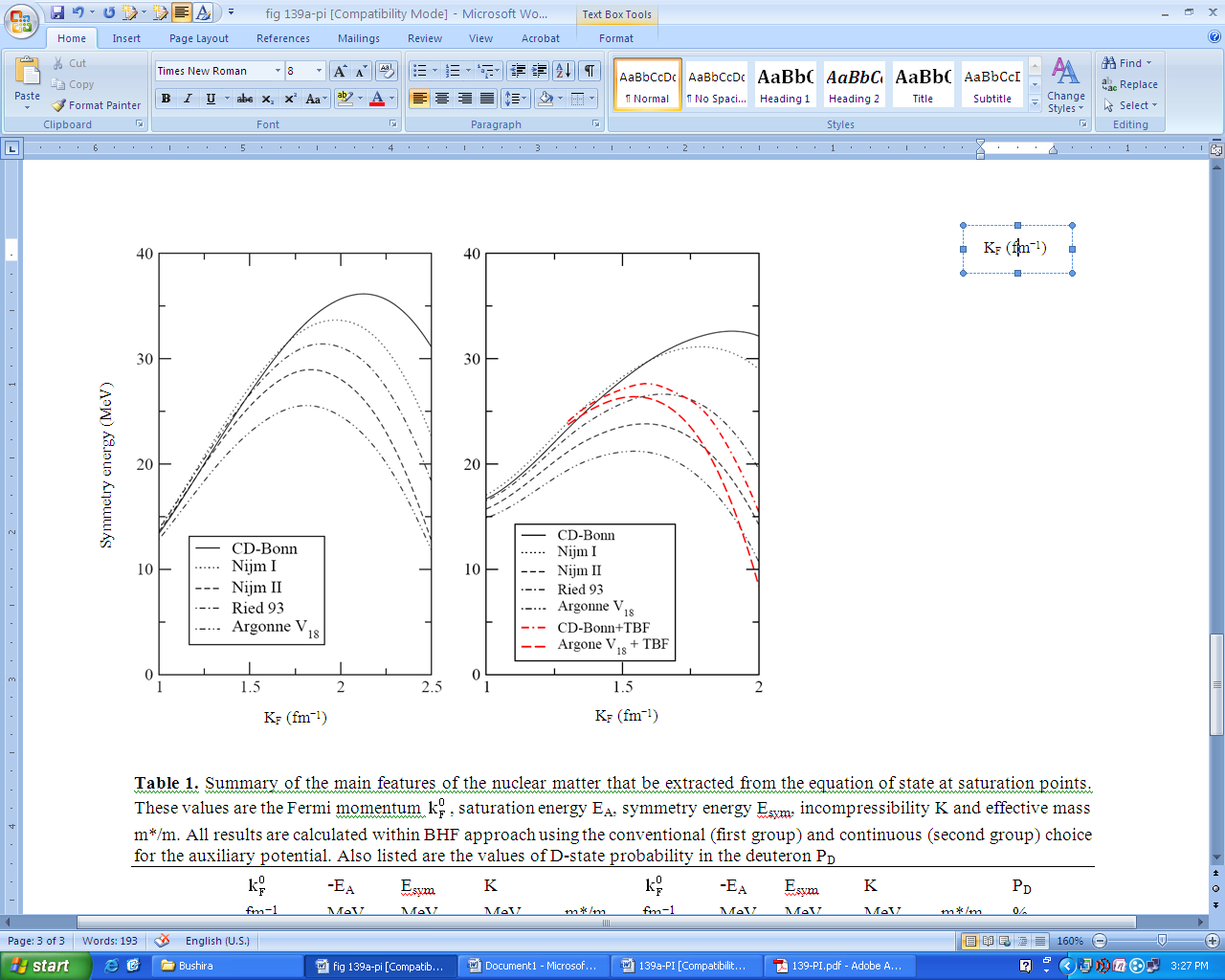 | Figure 5. The symmetry energy obtained from Equation (28) as a function of the Fermi momentum kF. The left panel represents conventional choice and the right panel with the continuous choice for the auxiliary potential |
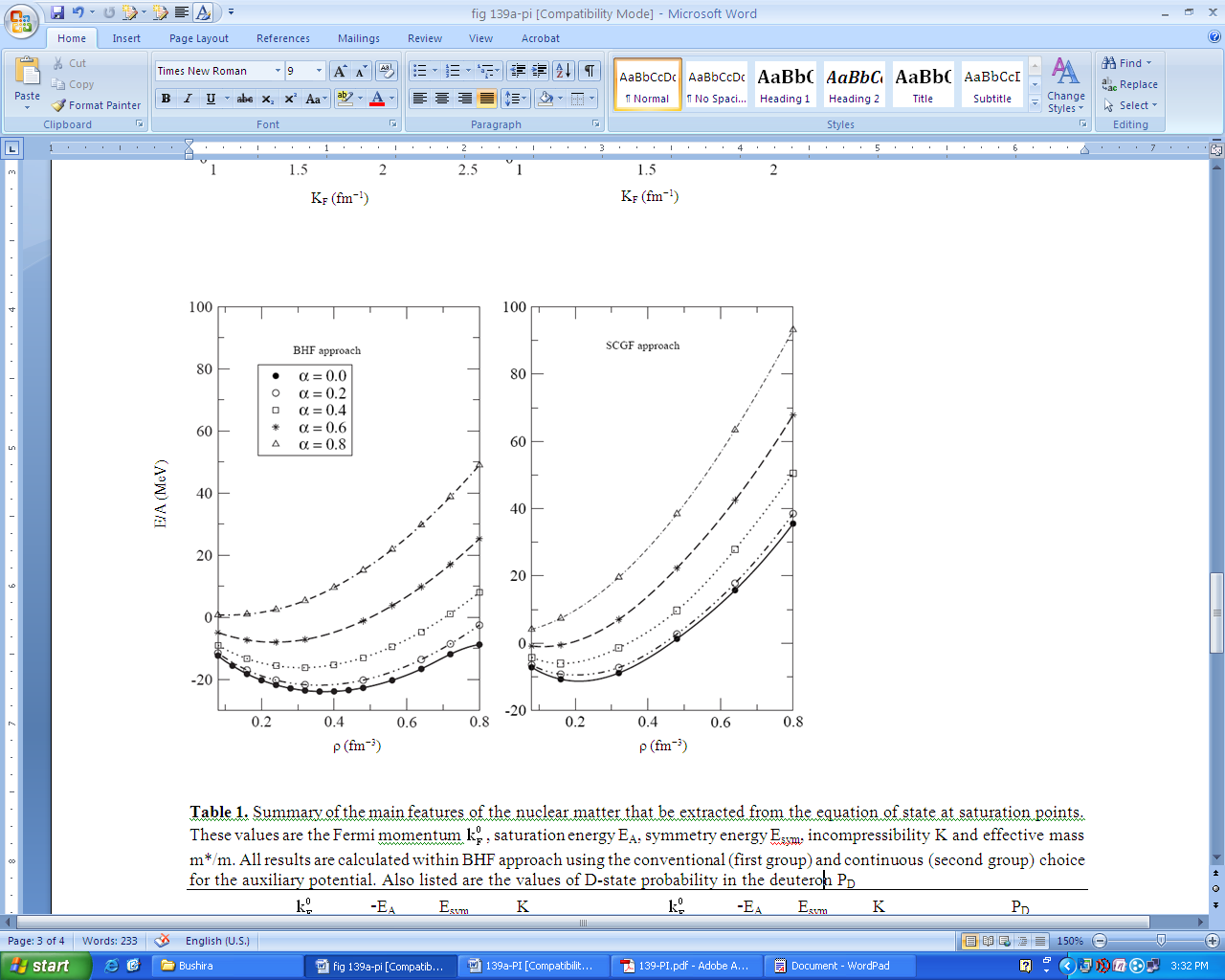 | Figure 6. The energy per nucleon for asymmetric nuclear matter as a function of density for various values of the asymmetry parameter α. The predictions are obtained from the BHF (left panel) and the SCGF (right panel) approaches |
|
|
2.5. The Symmetry Energy and its Relation with the Chemical Potential
- Within the parabolic approximation (Eq. 16) in[34] one can obtain the neutron and proton chemical potentials in asymmetric nuclear matter in the following way[55, 56]:
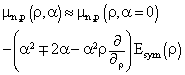 | (30) |
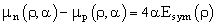 | (31) |
2.6. Properties of Asymmetric Nuclear Matter
2.6.1. How to Reproduce the Empirical Saturation Point
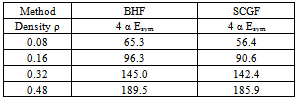
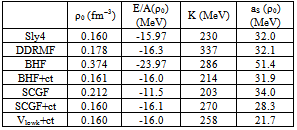
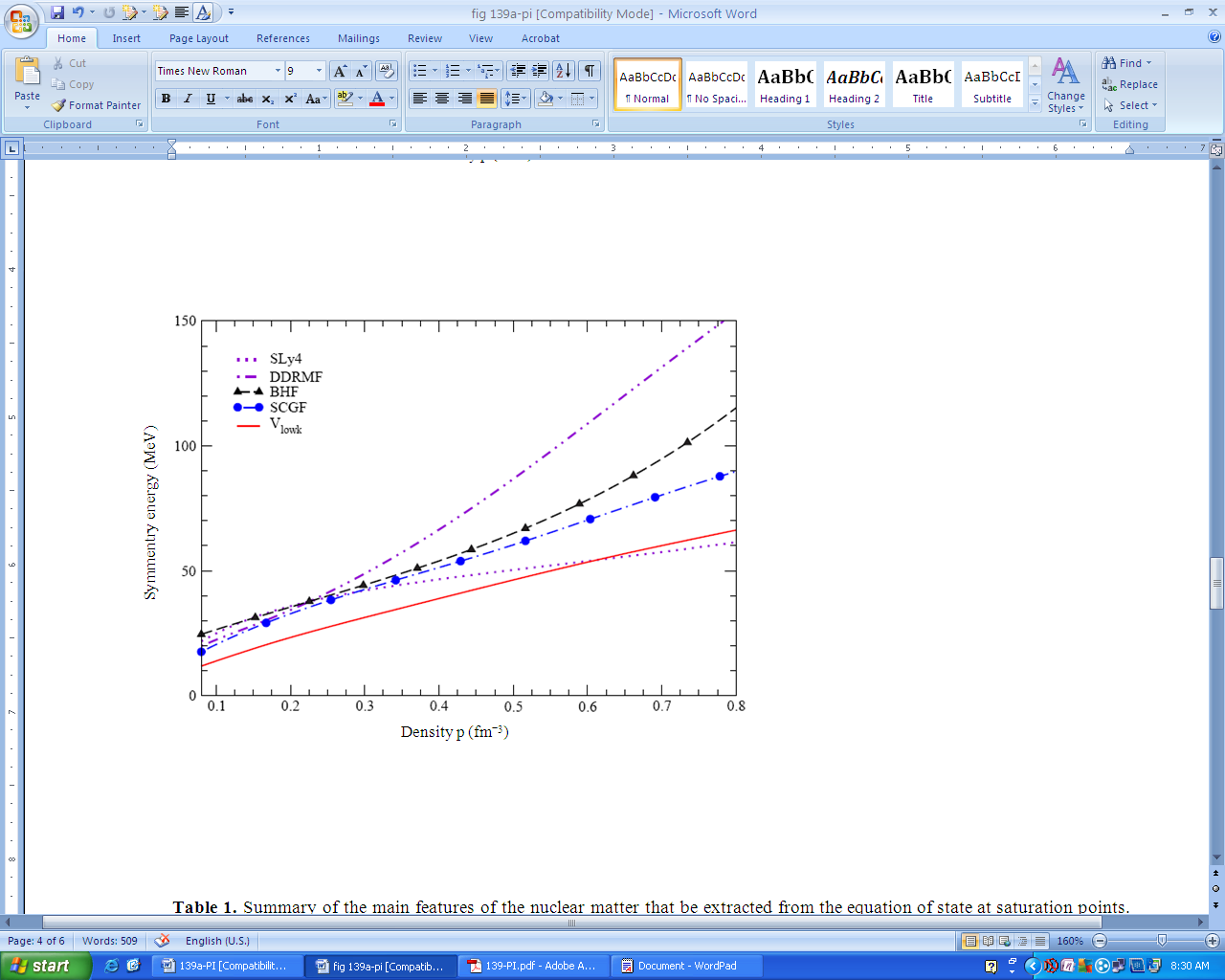
- All results of calculations, which refer to realistic NN interactions, have been obtained using the CD-Bonn[7] interaction. This includes all BHF and SCGF calculations. Also the evaluation of Vlowk has been based on the proton-neutron part of CD-Bonn. The Skyrme Hartree-Fock calculations have been done using the parameterization SLy4 and for the relativistic mean-field calculation the parameterization for DDRMF in[57] has been used.First let us turn to the binding energy of symmetric nuclear matter, which are displayed in Fig. 7. Compared to other realistic NN interactions the CD-Bonn potential, which we have chosen here is a rather soft NN interaction with a weak tensor force. This is indicated by the results for the saturation point of symmetric nuclear matter as obtained in the BHF approximation (the minimum of the dashed black line in Fig. 7 and data in Table 4). The saturation density is larger than twice the empirical value and the calculated energy is well below, which means that the CD-Bonn result is located in the large binding energy high density part of the Coester band[1].In order to reproduce the empirical saturation point of symmetric nuclear we have added an isoscalar interaction term as defined in Eq. (21) choosing a value for δ = 0.5 and fitting the parameters t0 and t3. The results for these fitting parameters are listed in Table 5 and the corresponding energy versus density curves are displayed in Fig. 7.
2.7. The Nuclear Compressibility Modulus or the Incompressibility
- The results for the calculated saturation points in Table 4 are supplemented by the corresponding values for the nuclear compressibility modulus:
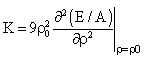 | (32) |
|
|
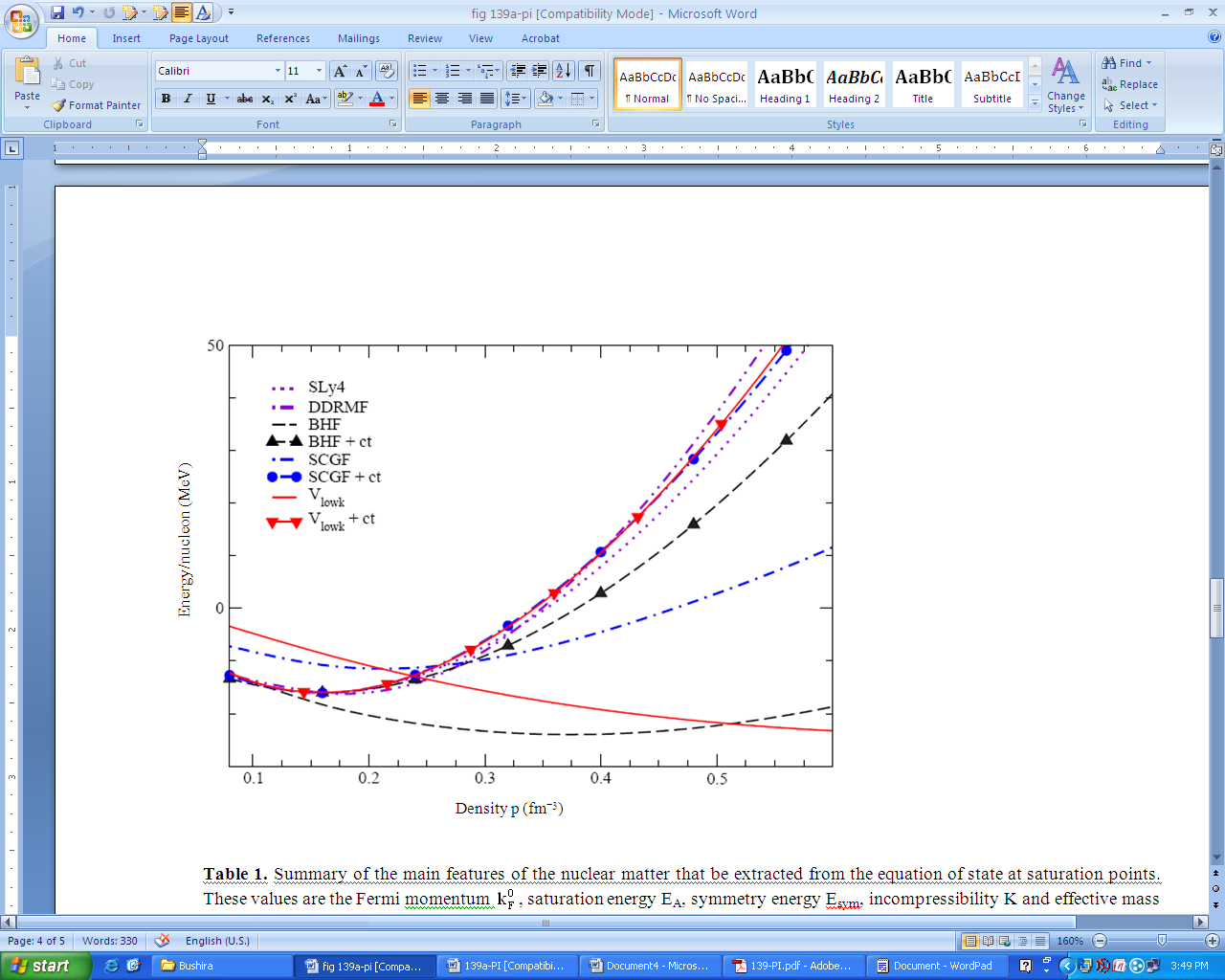 | Figure 7. (Color online) Comparison of binding energy per nucleon of symmetric nuclear matter as obtained from Skyrme SLy4, DDRMF, BHF, SCGF and Vlowk. Results of approaches based on realistic NN interactions are also compared with an additional contact interaction of the form displayed in Eq. (21) |
2.8. The Nuclear Symmetry Energy
- Table 5 also displays results for the symmetry energy:
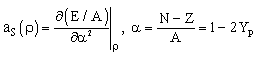 | (33) |
 | Figure 8. (Color online) Comparison of the symmetry energy aS(ρ) as a function of density ρ as obtained from Skyrme SLy4, DDRMF, BHF, SCGF and Vlowk approaches |
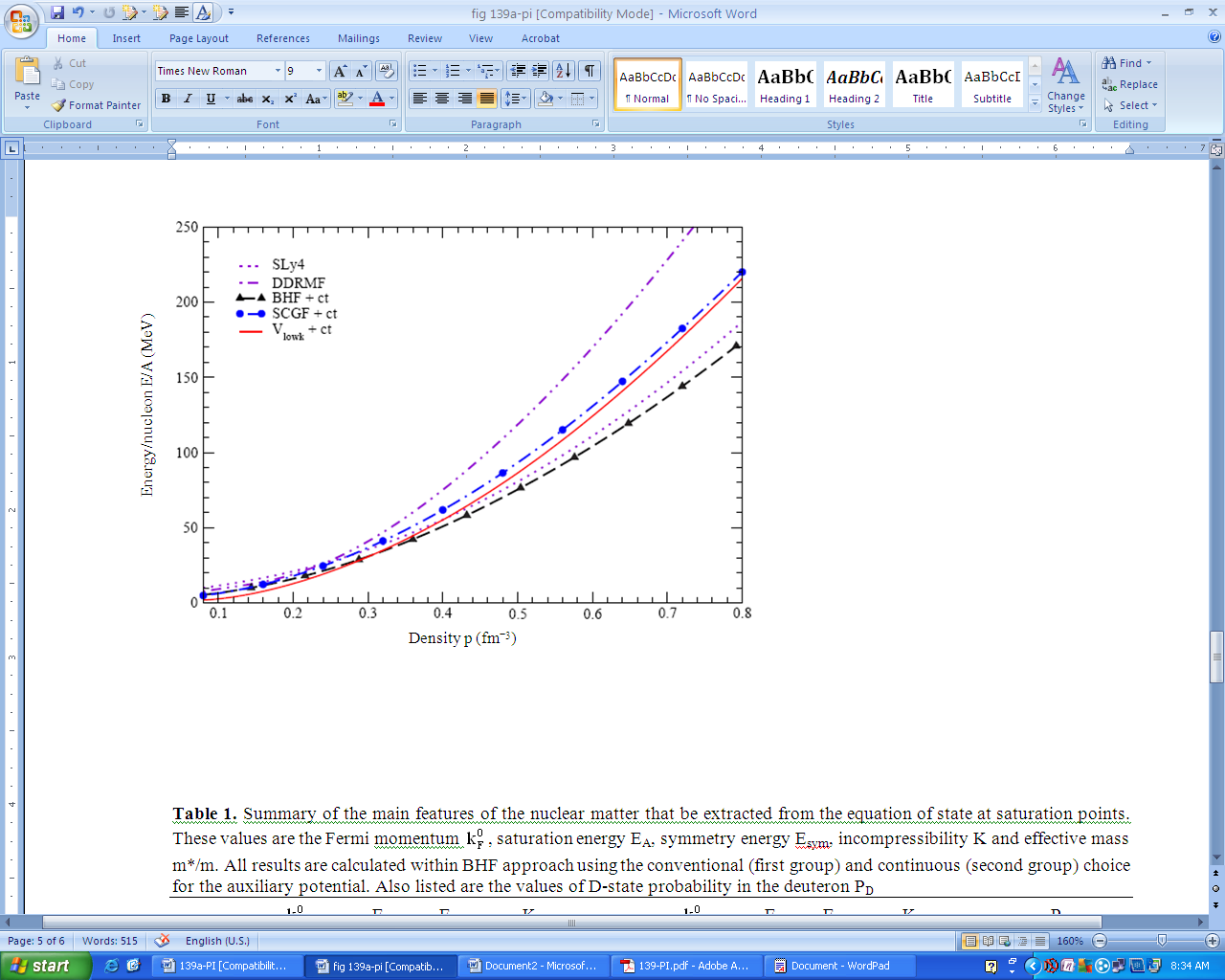 | Figure 9. (Color online) Energy per nucleon of pure neutron matter as a function of density as obtained from Skyrme SLy4, DDRMF, BHF, SCGF and Vlowk approaches |
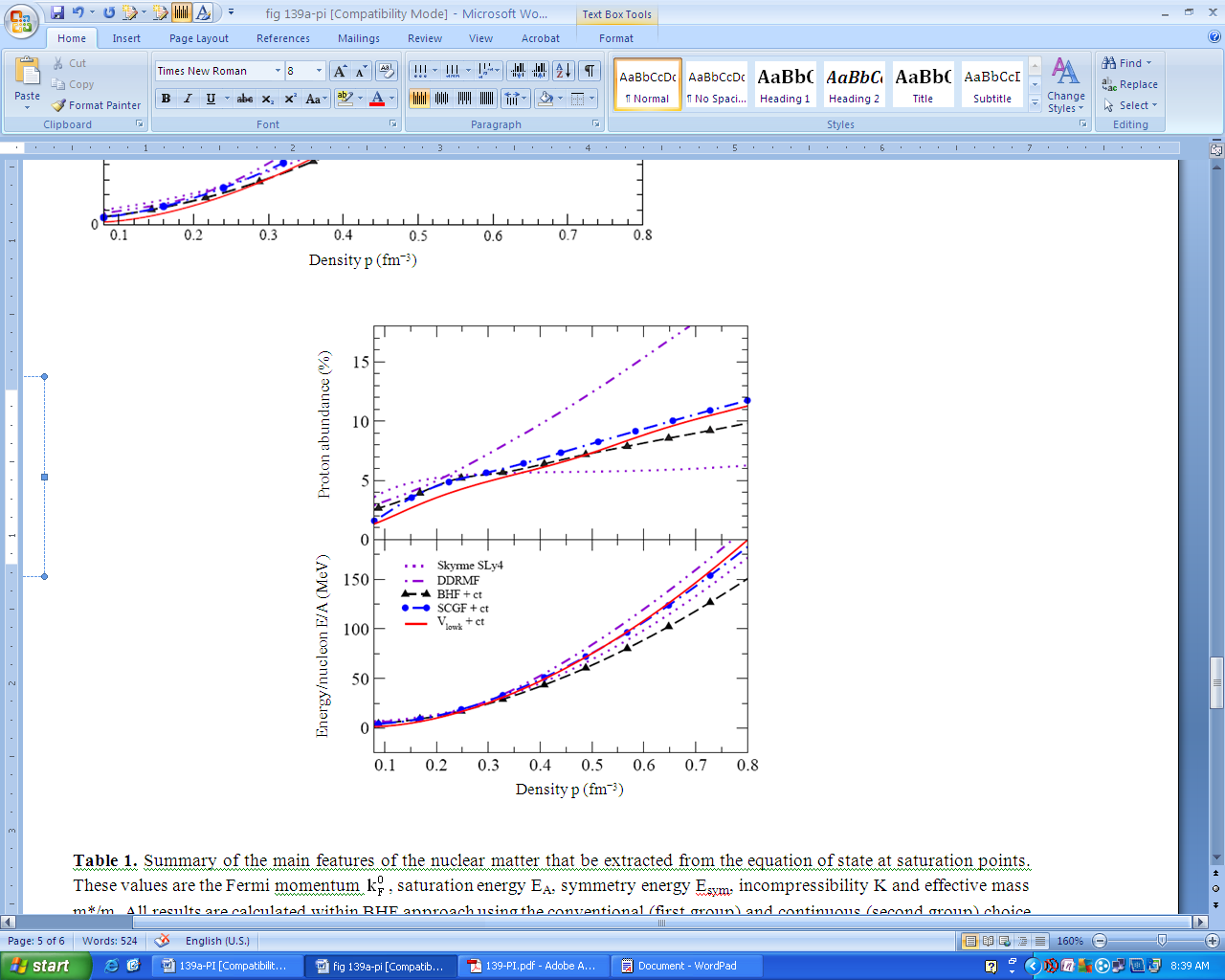 | Figure 10. (Color online) Results for a system of infinite matter consisting of protons, neutrons and electrons in β-equilibrium. The upper panel show the proton abundances and the lower panel displays the energy per nucleon as a function of density using the various approximation schemes discussed in the text |
2.9. β-Equilibrium
- Rather similar features also observed, when we inspect the properties of nuclear matter in β-equilibrium, neutralizing the charge of the protons by electrons, displayed in Fig. 10. The upper panel of this figure displays the proton abundance Yp = Z/A, which are to some extent related to the symmetry energy: large symmetry energy should correspond to large proton abundances. So the largest proton abundances are predicted within the DDRMF approach. Already at a density around 0.4 fm3 Yp exceeds the about 10%, which implies that the direct URCA process could be enabled, which should be reflected in a fast cooling of a neutron star.The Vlowk and SCGF approaches lead to similar proton abundances at large densities. This demonstrates that the evaluation of the proton abundance in β-equilibrium cannot directly be deduced from the symmetry energy, since the former observable is derived from proton and neutron energies at large asymmetries (Z<
2.10. The Isovector Effective Mass
- Another important information for the evaluation of dynamical features of matter in neutron stars is the density of states, which can be characterized by an effective mass. The term effective mass is used in various connections in many-body physics. This includes the effective masses, which express the non-locality of the self-energy in space and time, which corresponds to a momentum and energy dependence. Such effective masses for protons and neutrons determined for nuclear matter in β-equilibrium are displayed in Fig. 11 as a function of density considering non-relativistic approximation schemes.It is a general feature of all approaches considered that the effective masses for protons as well as neutrons decrease with increasing density. However, there is a striking difference between the phenomenological Skyrme approximation and the BHF and Vlowk approach, which are based on realistic NN interactions: The effective mass for protons is smaller than the corresponding one for neutrons in neutron rich matter for the calculations using realistic interactions, while it is opposite applying the Skyrme parameterization. In fact, if we define the effective masses for protons m
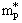 and neutrons
and neutrons 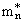 in terms of isoscalar
in terms of isoscalar 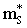 and isovector masses
and isovector masses 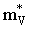 by:
by: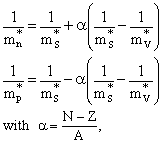 | (34) |
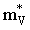 , which is even larger than the bare nucleon mass M[61] which implies that it is larger than the effective isoscalar mass
, which is even larger than the bare nucleon mass M[61] which implies that it is larger than the effective isoscalar mass 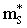 . This means that the effective mass for neutrons is smaller than the corresponding one for the protons in neutron rich matter (α>0). These Skyrme parameterizations leading to a large effective isovector mass are usually favored as they correspond within the mean-field approach to an enhancement factor k of the Thomas-Reiche-Kuhn sum-rule[62, 63].Non-relativistic descriptions of nuclear matter, which are based on realistic interactions yield an effective isovector mass
. This means that the effective mass for neutrons is smaller than the corresponding one for the protons in neutron rich matter (α>0). These Skyrme parameterizations leading to a large effective isovector mass are usually favored as they correspond within the mean-field approach to an enhancement factor k of the Thomas-Reiche-Kuhn sum-rule[62, 63].Non-relativistic descriptions of nuclear matter, which are based on realistic interactions yield an effective isovector mass 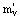 which is smaller than the corresponding effective isoscalar mass, which leads to a larger effective mass for neutrons than for protons in neutron-rich matter (Fig. 11). In order to analyze this finding we inspect the dependence of the nucleon self-energy in the BHF approximation
which is smaller than the corresponding effective isoscalar mass, which leads to a larger effective mass for neutrons than for protons in neutron-rich matter (Fig. 11). In order to analyze this finding we inspect the dependence of the nucleon self-energy in the BHF approximation 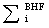 , defined in Eq. (7), as a function of energy ω and momentum k of the nucleon considered. Following the discussion of Mahaux and Sartor[38] one can define the effective k-mass:
, defined in Eq. (7), as a function of energy ω and momentum k of the nucleon considered. Following the discussion of Mahaux and Sartor[38] one can define the effective k-mass: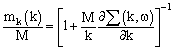 | (35) |
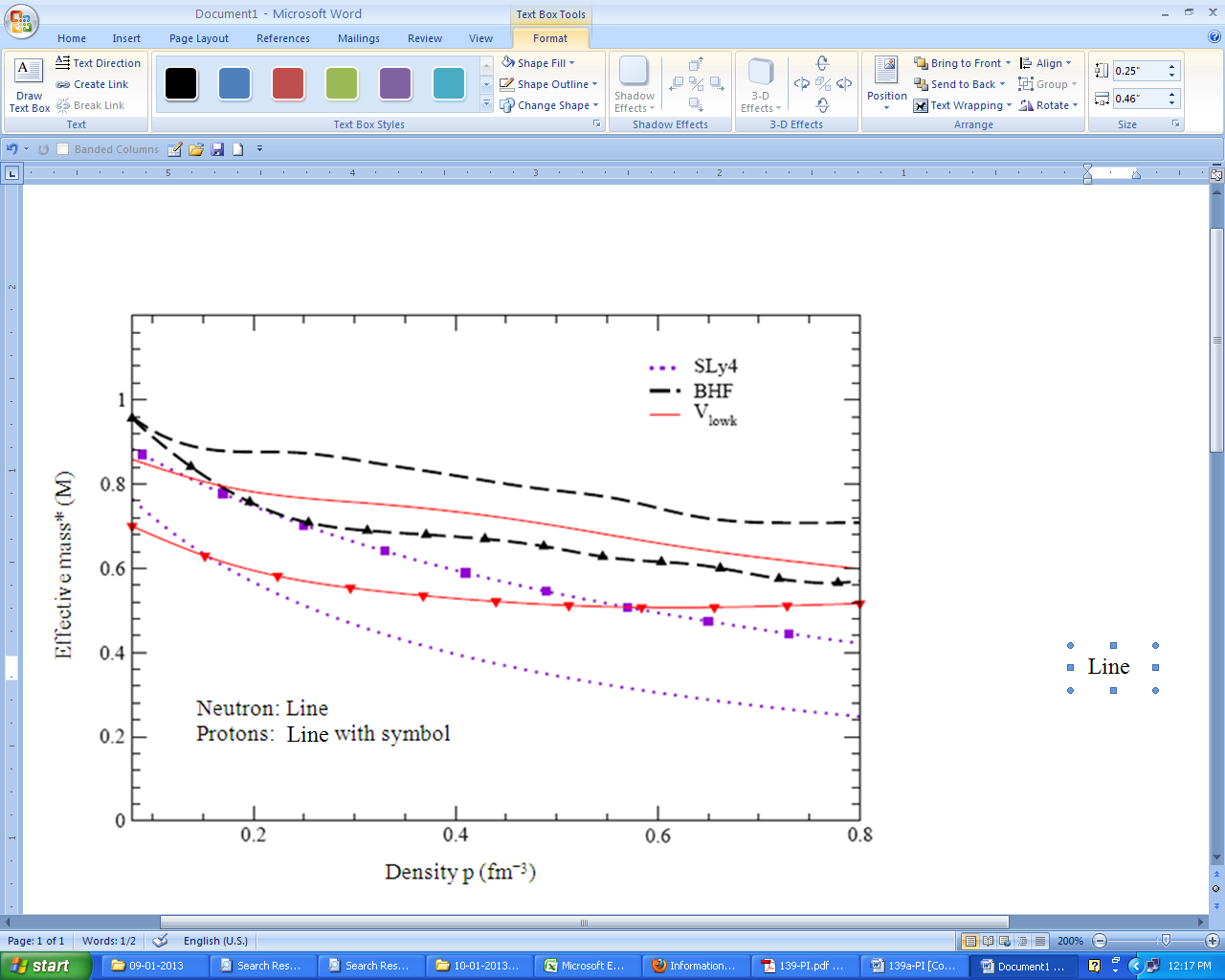 | Figure 11. (Color online) Effective masses for protons (lines with symbols) and neutrons (lines without symbols) as obtained for nuclear matter in β-equilibrium using Skyrme HF (SLy4), BHF and Vlowk approaches |
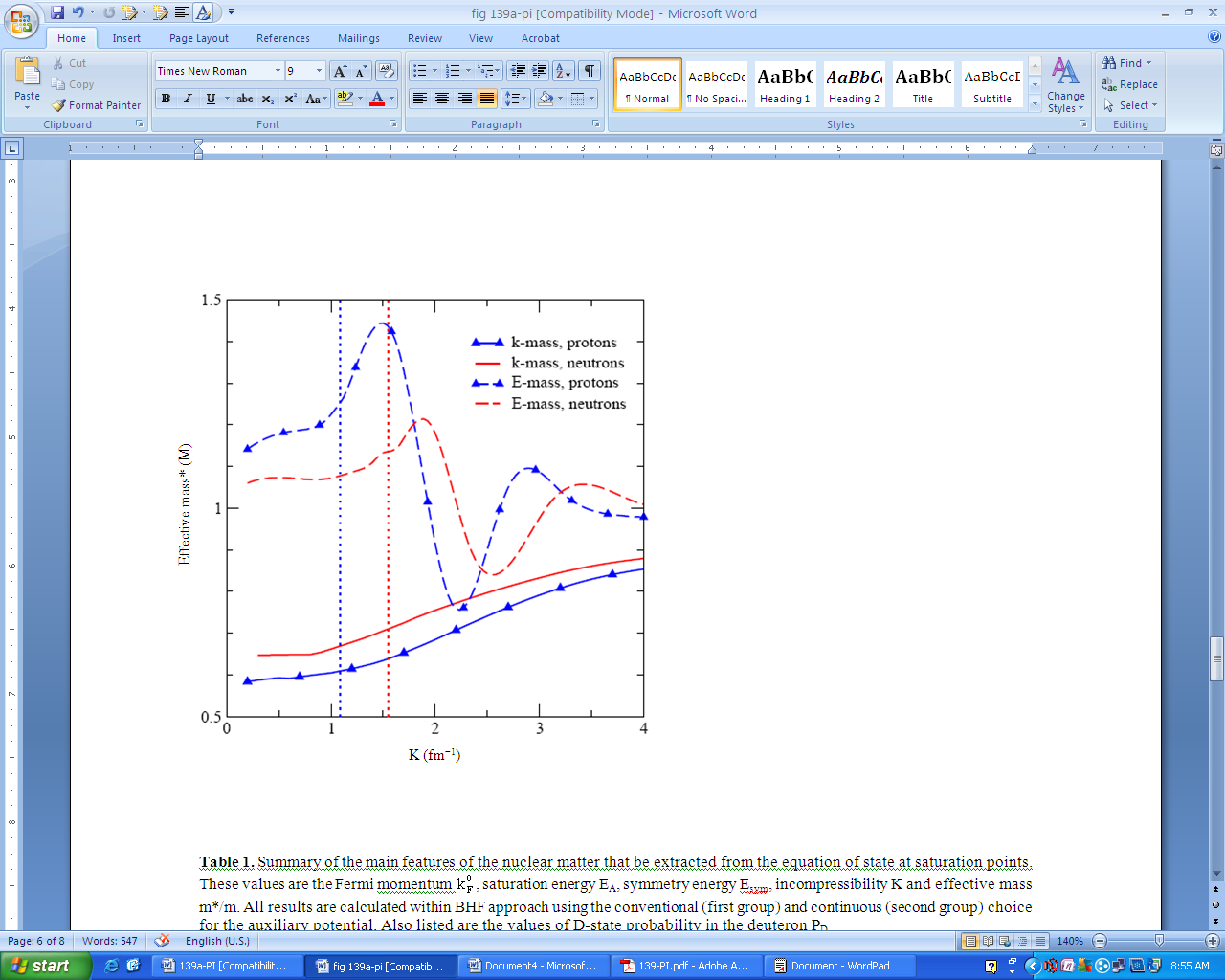 | Figure 12. (Color online) Effective k-mass 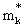 k) (solid lines) and effective E-mass k) (solid lines) and effective E-mass 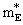 (k) (dashed lines) for neutrons and protons (lines with symbol) as obtained from the BHF calculations for asymmetric nuclear matter at the density ρ = 0.17 fm3 and a proton abundance of 25%. The Fermi momenta for protons and neutrons are indicated by vertical dotted lines (k) (dashed lines) for neutrons and protons (lines with symbol) as obtained from the BHF calculations for asymmetric nuclear matter at the density ρ = 0.17 fm3 and a proton abundance of 25%. The Fermi momenta for protons and neutrons are indicated by vertical dotted lines |
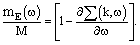 | (36) |
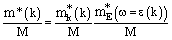 | (37) |
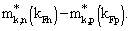 The effective k-mass describes the non-locality of the BHF self-energy. This non-locality and thereby also these features of the effective k-mass are rather independent on the realistic interaction used. Furthermore it turns out that the values for the k-mass are essentially identical if one derives them from the nucleon BHF self-energy using the G-matrix or from the bare interaction V or from Vlowk[2]. This non-locality of the self-energy is dominated by Fockexchange contribution originating from ρ-exchange. In neutron-rich matter this contribution leads to a stronger depletion for the proton mass than for the neutron mass[4, 64].Anyway, the enhancement of the effective mass m*, which is due to the effective E-mass in Equation (34) is not strong enough to compensate the effects of the k-mass. Therefore the final effective mass is below the bare mass M and the effective mass for neutrons remains larger than the corresponding one for protons.
The effective k-mass describes the non-locality of the BHF self-energy. This non-locality and thereby also these features of the effective k-mass are rather independent on the realistic interaction used. Furthermore it turns out that the values for the k-mass are essentially identical if one derives them from the nucleon BHF self-energy using the G-matrix or from the bare interaction V or from Vlowk[2]. This non-locality of the self-energy is dominated by Fockexchange contribution originating from ρ-exchange. In neutron-rich matter this contribution leads to a stronger depletion for the proton mass than for the neutron mass[4, 64].Anyway, the enhancement of the effective mass m*, which is due to the effective E-mass in Equation (34) is not strong enough to compensate the effects of the k-mass. Therefore the final effective mass is below the bare mass M and the effective mass for neutrons remains larger than the corresponding one for protons.2.11. The Symmetry Potential Usym
- Regarding Un/p as functions of the asymmetry parameter a, one can easily verify that the following approximate relation applies:
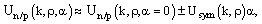 | (38) |
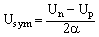 | (39) |
2.12. Free Energy of the Symmetric Nuclear Matter at Finite Temperatures
- Many attempts were made to use the BHF calculations at finite temperature[8, 43, 66, 67]. In Fig. 14, the internal energy F of nuclear matter in MeV is plotted against the density ρ in fm-3 and the values obtained with the low temperature expansion (26). The results are shown in Fig. 14, for symmetric nuclear matter using different potentials. For both T = 8 (upper graph) and T = 12 MeV (lower one), for continuous choice. Fig. 14 gives the results obtained using the CD-Bonn potential (solid line), the Nijm1 potential (dashed line) and the Reid 93 potential (dashed–dot line) in comparison with a more elaborate calculation using Argonne V14 plus microscopic 3BF[43] (dashed double dotted line). From the plotted figures it is observed that the internal energy first decreases with increasing the density until it reaches a minimum then it increases with increasing the density. Our results are comparable to those obtained in Ref.[43]. The same results have been done using the conventional choice of the auxiliary potential in Ref.[68].
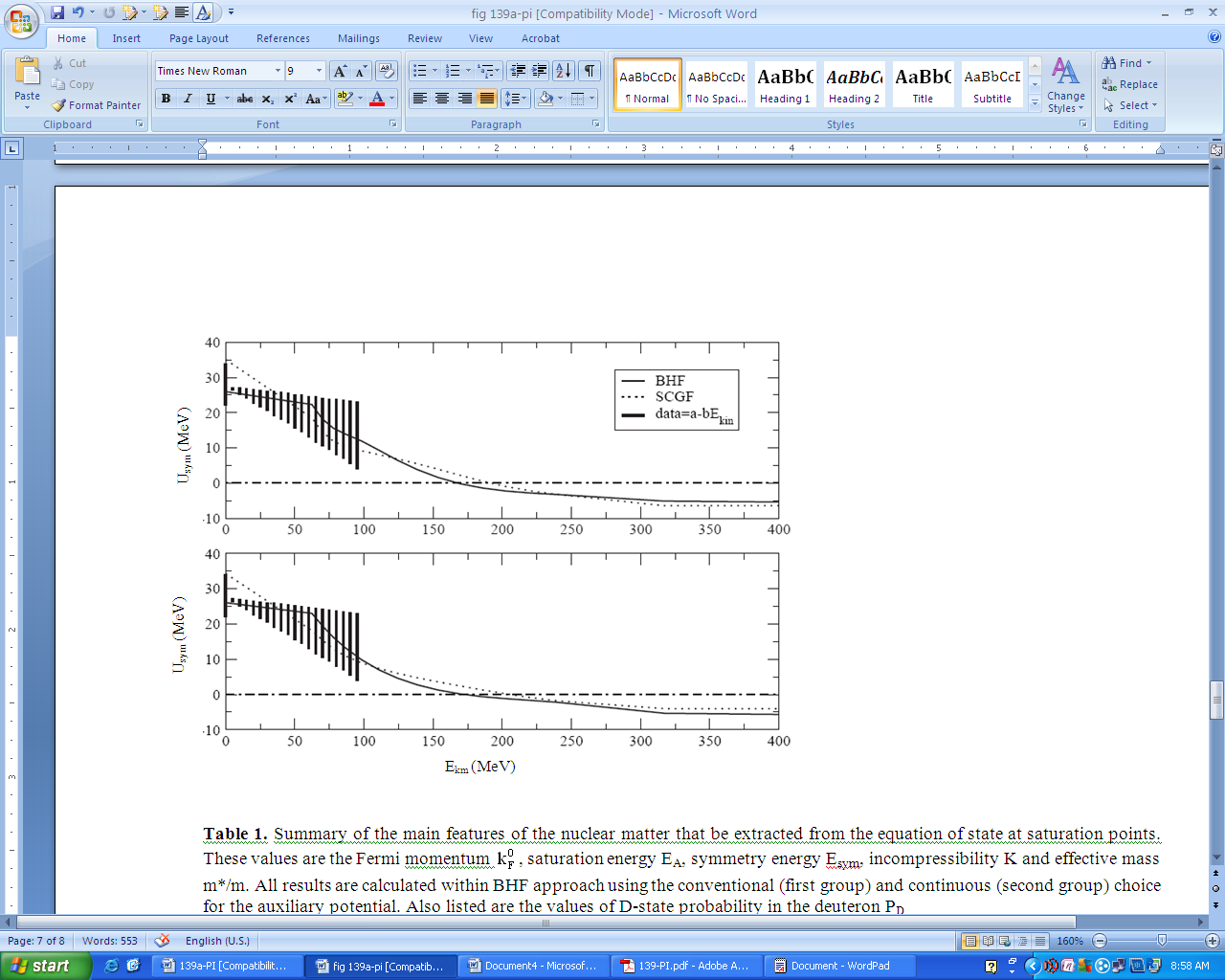 | Figure 13. The symmetry potential as a function of the nucleon kinetic energy at nuclear matter density (ρ = 0.16 fm3) and at asymmetry parameter δ = 0.2 (upper panel) and at δ = 0.4 (lower panel). The predictions are obtained with the CD-Bonn potential and compared with the empirical information from the nuclear optical potential data (shaded area) |
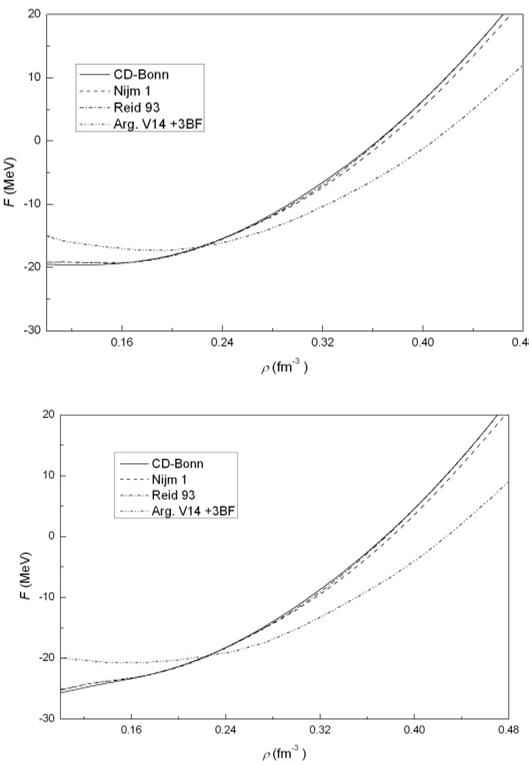 | Figure 14. The internal energy at T = 8 MeV (upper figure) and T=12 MeV (lower one) for symmetric nuclear matter as a function of density using different potentials for continuous choice compared with Argonne V14 plus microscopic 3BF by Baldo and Ferreira[43] |
3. Conclusions
- We have investigated the effect of different modern nucleon-nucleon potentials on the EoS, i.e., the nuclear matter binding energy per nucleon, within BHF approach. It is found that our calculations lead to results, which lie along a line (Coester line) shifted with respect to the phenomenological saturation point (ρ0 = 0.16 fm-3, EA = -16 MeV).We have reviewed the current status of the Coester line, i.e., the saturation points of nuclear matter obtained within BHF approach using the conventional and continuous choice for the auxiliary potential and employing the modern nucleon-nucleon potentials. It is found that our results confirm the concept of a “line”, density and energy of the various saturation points being strongly linearly correlated.We have presented a microscopic calculation of the equation of state of nuclear matte when protons and neutrons have different Fermi momenta. The techniques to evaluate the single-particle green’s function in a Self-Consistent G-matrix approach (SCGF). The continuous choice has been adopted for the auxiliary potential. The single-particle energy is calculated self-consistently using BHF and SCGF approximations. The contribution of the hh terms leads to a repulsive contribution to the single-particle energy which decreases with momentum. The dependence of the EoS on the neutron excess parameter is clearly linear as a function of a2. The inclusion of the hole-hole ladders and the self-consistent treatment of the Green’s function in the SCGF approach leads to a small reduction of the binding energy per nucleon as compared to the BHF approximation.Various approaches to the nuclear many-body problem have been investigated to explore their predictions for nuclear matter at high density and large proton-neutron asymmetries. Two of these approaches, the Skyrme Hartree-Fock and the Density Dependent Relativistic Mean Field approach are predominantly of phenomenological origin. Their parameters have been adjusted to reproduce data of finite nuclei. However, the parameters have been selected in such a way that also bulk properties of asymmetric nuclear matter derived from microscopic calculations are reproduced. The other three approaches are based on realistic NN interactions, which fit the NN scattering phase shifts. In these approximation schemes (Brueckner Hartree Fock BHF, Self-consistent Greens Function SCGF and Hartree Fock using a renormalized interaction Vlowk) a isoscalar contact interaction has been added to reproduce the empirical saturation point of symmetric nuclear matter.These various approximation schemes lead to rather similar predictions for the energy per nucleon of symmetric and asymmetric nuclear matter at high densities. In detail one finds that the relativistic DDRMF leads to a rather stiff Equation of State (EoS) for symmetric matter while the BHF approach leads to a relatively soft EoS, a feature which is compensated within the microscopic framework by the repulsive features of the hole-hole ladders included in SCGF. These features are also reflected in the study of nuclear matter in the β-equilibrium and lead to moderate differences in the predictions for proton abundances and EoS.More significant differences are observed when we inspect details like the effective masses, in particular the isovector effective mass. In neutron-rich matter the microscopic approaches predict a positive difference between neutron and proton effective masses. This feature can be related to the non-locality of the self-energy induced by one-pion exchange term and is expressed in terms of an effective k-mass.Also the symmetry potential has been calculated as a function of the nucleon kinetic energy. We observe that the strength of the predicted symmetry potential decreases with energy, a behavior which is consistent with the empirical information. It is interesting to note that at normal density (ρ = 0.16 fm3), the nuclear symmetry potential changes from positive to negative values at nucleon kinetic energy around 200 MeV. More details can be read in Ref.[69].
ACKNOWLEDGMENTS
- The authers would like to thank Prof. H. Müther.
References
| [1] | H. Müther and A. Polls, Prog. Part. Nucl. Phys., 45: 243 (2000). |
| [2] | T. Frick, K. Gad, H. Müther and P. Czerski, Phys. Rev., C 65: 034321, (2002). |
| [3] | T. Frick, Kh.S.A. Hassaneen, D. Rohe and H. Müther, Phys. Rev. C 70: 024309, (2004). |
| [4] | Kh.S.A. Hassaneen and H. Müther, Phys. Rev. C 70: 054308, (2004). |
| [5] | V.G.J. Stoks, R.A.M. Klomp, C.P.F. Terheggen and J.J.D. Swart, Construction of high-quality NN potential models. Phys. Rev. C 49: 2950-2962. DOI:10.1103/PhysRevC.49.2950, (1994) |
| [6] | R.B. Wiringa, V.G.J. Stoks and R. Schiavilla, Phys. Rev. C 51: 38, (1995). |
| [7] | R. Machleidt, F. Sammarruca and Y. Song, Phys. Rev. C 53: R1483, (1996); R. Machleidt, Phys. Rev., C 63: 024001, (2001). |
| [8] | T. Frick and H. Müther, Phys. Rev. C 68: 034310, (2003). |
| [9] | A.E.L. Dieperink, Y. Dewulf, D.V. Neck, M. Waroquier and V. Rodin, Phys. Rev. C 68: 064307, (2003). |
| [10] | W. Zuo, I. Bombaci and U. Lombardo, Asymmetric nuclear matter from an extended Brueckner-Hartree-Fock approach. Phys. Rev. C 60: 024605-024617. DOI:10.1103/PhysRevC.60.024605, (1999). |
| [11] | I. Vidana and I. Bombaci, Equation of state and magnetic susceptibility of spin polarized isospin asymmetric nuclear matter. Phys. Rev. C 66: 045801-045811. DOI:10.1103/PhysRevC.66.045801, (2002). |
| [12] | K.A. Brueckner and J.L. Gammel, Properties of nuclear matter. Phys. Rev. 109: 1023-1039. DOI:10.1103/PhysRev.109.1023, (1958). |
| [13] | H. Müther, M. Prakash and T.L. Ainsworth, The nuclear symmetry energy in relativistic Brueckner-Hartree-Fock calculations. Phys. Lett. B 199: 469-474. DOI:10.1016/0370-2693(87)91611-X , (1987). |
| [14] | L. Engivik, M. Hjorth-Jensen, E. Osnes, G. Bao and E. Ostgaard, Asymmetric nuclear matter and neutron star properties. Phys. Rev. Lett. 73: 2650-2653. DOI:10.1103/PhysRevLett.73.2650, (1994). |
| [15] | F. Hofmann, C.M. Keil and H. Lenske, Density dependent hadron field theory for asymmetric nuclear matter and exotic nuclei. Phys. Rev. C 64: 034314-034229. DOI:10.1103/PhysRevC.64.034314, (2001). |
| [16] | D. Alonso and F. Sammarruca, Microscopic calculations in asymmetric nuclear matter. Phys. Rev. C 67: 054301-054301. DOI: 10.1103/PhysRevC.67.054301, (2003). |
| [17] | I. Bombaci and U. Lombardo, Asymmetric nuclear matter equation of state. Phys. Rev. C 44: 1892-1900. DOI: 10.1103/PhysRevC.44.1892, (1991). |
| [18] | H.Q. Song, M. Baldo, G. Giansiracusa, U. Lombardo, Phys. Rev. Lett. 81, 1584, (1998). |
| [19] | R.B. Wiringa, V. Fiks and A. Fabrocini, Phys. Rev. C 38: 1010, (1988). |
| [20] | A. Akmal and V.R. Pandharipande, Phys. Rev. C 56: 2261, (1997). |
| [21] | Y. Sugahara and H. Toki, Nucl. Phys. A 579: 557, 1994; Akmal, A., V.R. Pandharipande and D.G. Ravenhall, Phys. Rev. C 58: 1804, (1998). |
| [22] | D. Vretenar, T. Niksic and P. Ring, Phys. Rev. C 68: 024310. (2003). |
| [23] | J.R. Stone, P.D. Stevenson, J.C. Miller and M.R. Strayer, Phys. Rev. C 65: 064312, (2002). |
| [24] | J.R. Stone, J.C. Miller, R. Koncewicz, P.D. Stevenson and M.R. Strayer, Phys. Rev. C 68: 034324, (2003). |
| [25] | P. Bozek, Phys. Lett. B 586: 239, (2004). |
| [26] | N.M. Hugenholtz and L.V. Hove, Physica 24: 363, (1958). |
| [27] | K. Gad, Eur. Phys. J. A 22: 405, (2004). |
| [28] | P. Bozek and P. Czerski, Eur. Phys. J. A 11: 271, (2001). |
| [29] | P. Bozek, Eur. Phys. J. A 15: 325, (2002). |
| [30] | W. Zuo, G. Giansiracusa, U. Lombardo, N. Sandulescu and H.J. Schulze, Single-particle properties in neutron matter from extended Brueckner theory. Phys. Lett. B 421: 1-7. DOI: 10.1016/S0370-2693(97)01600-6, (1998). |
| [31] | B.A. Li, L.W. Chen and C.M. Ko, Recent progress and new challenges in isospin physics with heavy-ion reactions. Phys. Rep. 464: 113-281. DOI: 10.1016/j.physrep.2008.04.005, (2008). |
| [32] | V. Baran, M. Colonna, V. Greco and M.D. Toro, Reaction dynamics with exotic nuclei. Phys. Rep. 410: 335-466. DOI: 10.1016/j.physrep.2004.12.004, (2005). |
| [33] | K. Gad and Kh.S.A. Hassaneen, Equation of state for neutron-rich matter with self-consistent green function approach. Nucl. Phys. A 793: 67-78. DOI:10.1016/j.nuclphysa.2007.06.015, (2007). |
| [34] | Kh. Hassaneen and K. Gad, The nuclear symmetry energy in self-consistent green-function calculations. J. Phys. Soc. Jpn. 77: 084201-084206. DOI: 10.1143/JPSJ.77.084201, (2008). |
| [35] | P. Gögelein, E.N.E.V. Dalen, K. Gad, Kh.S.A. Hassaneen and H. Müther, Properties of asymmetric nuclear matter in different approaches. Phys. Rev. C 79: 024308-024320. DOI: 10.1103/PhysRevC.79.024308, (2009). |
| [36] | Z.H. Li, U. Lombardo, H.J. Schulze, L.W. Zuo and L.W. Chen, Nuclear matter saturation point and symmetry energy with modern nucleon-nucleon potentials. Phys. Rev. C 74: 047304-047307. DOI: 10.1103/PhysRevC.74.047304, (2006). |
| [37] | M.I. Haftel and F. Tabakin, Nuclear saturation and the smoothness of nucleon-nucleon potentials. Nucl. Phys. A 158: 1-42. DOI: 10.1016/0375-9474(70)90047-3, (1970). |
| [38] | C. Mahaux and R. Sartor, Adv. Nucl. Phys. 20: 1, (1991). |
| [39] | P. Grange, J. Cugnon and A. Lejeune, Nucl. Phys. A 473: 365, (1987). |
| [40] | A. L. Fetter and J. D. Walecka, Quantum Theory of Many Particle Physics (McGraw-Hill, New York), (1971). |
| [41] | P. A. Henning, Phys. Rept. 253: 235, (1995). |
| [42] | C. Bloch, Nucl. Phys. 7: 451 (1958); C. Bloch and C. De Domicis, Nucl. Phys. 7, 459; 10: 509, (1958). |
| [43] | M. Baldo and L.S. Ferreira, Nuclear liquid-gas phase transition. Phys. Rev. C 59: 682-703. DOI:10.1103/PhysRevC.59.682, (1999). |
| [44] | H. Mansour, M. Hammad, and M.Y.M. Hassan, Phys. Rev. C 56: 1418, (1997). |
| [45] | M. Barranco and J. Treiner, Self-consistent description of nuclear of level densities. Nucl. Phys. A 351: 269-284. DOI: 10.1016/0375-9474(81)90444-9, (1981). |
| [46] | Kh.S.A. Hassaneen, H.M. Abo-Elsebaa, E.A. Sultan and H. Mansour, Nuclear binding energy and symmetry energy of nuclear matter with modern nucleon-nucleon potentials. Annals Phys. 326: 566-577. DOI: 10.1016/j.aop.2010.11.010, (2011) |
| [47] | M. Baldo and A. Fiasconaro, Single particle spectrum and binding energy of nuclear matter. Phys. Lett. B 491: 240-244. DOI: 10.1016/S0370-2693(00)01052-2, (2000) |
| [48] | B.D. Day, Nuclear Saturation from Two-Nucleon Potentials. Phys. Rev. Lett. 47: 226-229. DOI:10.1103/PhysRevLett.47.226, (1981). |
| [49] | M. Hjorth-Jensen, T.T.S. Kuo, and E. Osnes, Phys. Rep. 261: 125, (1995). |
| [50] | V. Somua and P. Bozek, Phys. Rev. C 78: 054003, (2008). |
| [51] | M. Baldo and A.E. Shaban, Phys. Lett. B 661: 373, (2008). |
| [52] | I. Bombaci and U. Lombardo, Phys. Rev. C 44: 1892, (1991). |
| [53] | P.E. Haustein, An overview of the 1986-1987 atomic mass predictions. Atomic Data Nuclear Data Tables, 39: 185-200. DOI: 10.1016/0092-640X(88)90019-8, (1988). |
| [54] | B.A. Li, Nucl. Phys. A 708: 365, (2002). |
| [55] | I. Vidana, A. Polls, A. Ramos, L. Engvik and M.Mjorth-Jensen, Phys. Rev. C 62: 035801, (2000). |
| [56] | M. Baldo, G.F. Burgio and H.J. Schulze, Phys. Rev. C 61: 055801, (2000). |
| [57] | P. Gögelein, E.N.E.V. Dalen, C. Fuchs and H. Müther, Phys. Rev. C 77: 025802, (2008). |
| [58] | A.E.L. Dieperink, Y. Dewulf, D.V. Neck, M. Waroquier and V. Rodin, Phys. Rev. C 68: 064307, (2003). |
| [59] | P. Gögelein and H. Müther, Phys. Rev. C 76: 024312, (2007). |
| [60] | L. Engvik, G. Bao, M. Hjorth-Jensen, E. Osnes, and E. Oestaard, Astrophys. J. 469: 794, (1996). |
| [61] | J.R. Stone and P.G. Reinhard, Prog. Part. Nucl. Phys. 56: 587, (2007). |
| [62] | P. Ring and P. Schuck, The Nuclear Many Body Problem, (Springer, Berlin Heidelberg New York, 1980). |
| [63] | M. Bender, P.H. Heenen, and P.G. Reinhard, Rev. Mod. Phys. 75: 121, (2003). |
| [64] | W. Zuo, L.G. Cao, B.A. Li, U. Lombardo and C.W. Shen, Phys. Rev. C 72: 014005, (2005). |
| [65] | A.M. Lane, Nucl. Phys. 35: 676, (1962). |
| [66] | I. Bombaci, A. Polls, A. Ramos, A. Rios, and I. Vidaña, Phys. Lett. B 632: 638, (2006). |
| [67] | A. Rios, A. Polls, and I. Vidaňa, Phys. Rev. C 71: 055802, (2005). |
| [68] | H. Mansour and Kh.S.A. Hassaneen, Nuclear and neutron matter properties using BHF approximation, Jour. Nucl. Part. Phys. 2(2): 14-21, DOI: 10.5923/j.jnpp.2012202.04, (2012). |
| [69] | H. Mansour, K. Gad, and Kh.S.A. Hassaneen, Self-Consistent Green Function Calculations for Isospin Asymmetric Nuclear Matter, Prog. Theor. Phys. 123: 687-700. DOI:10.1143/PTP.123.687 , (2010). |
 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML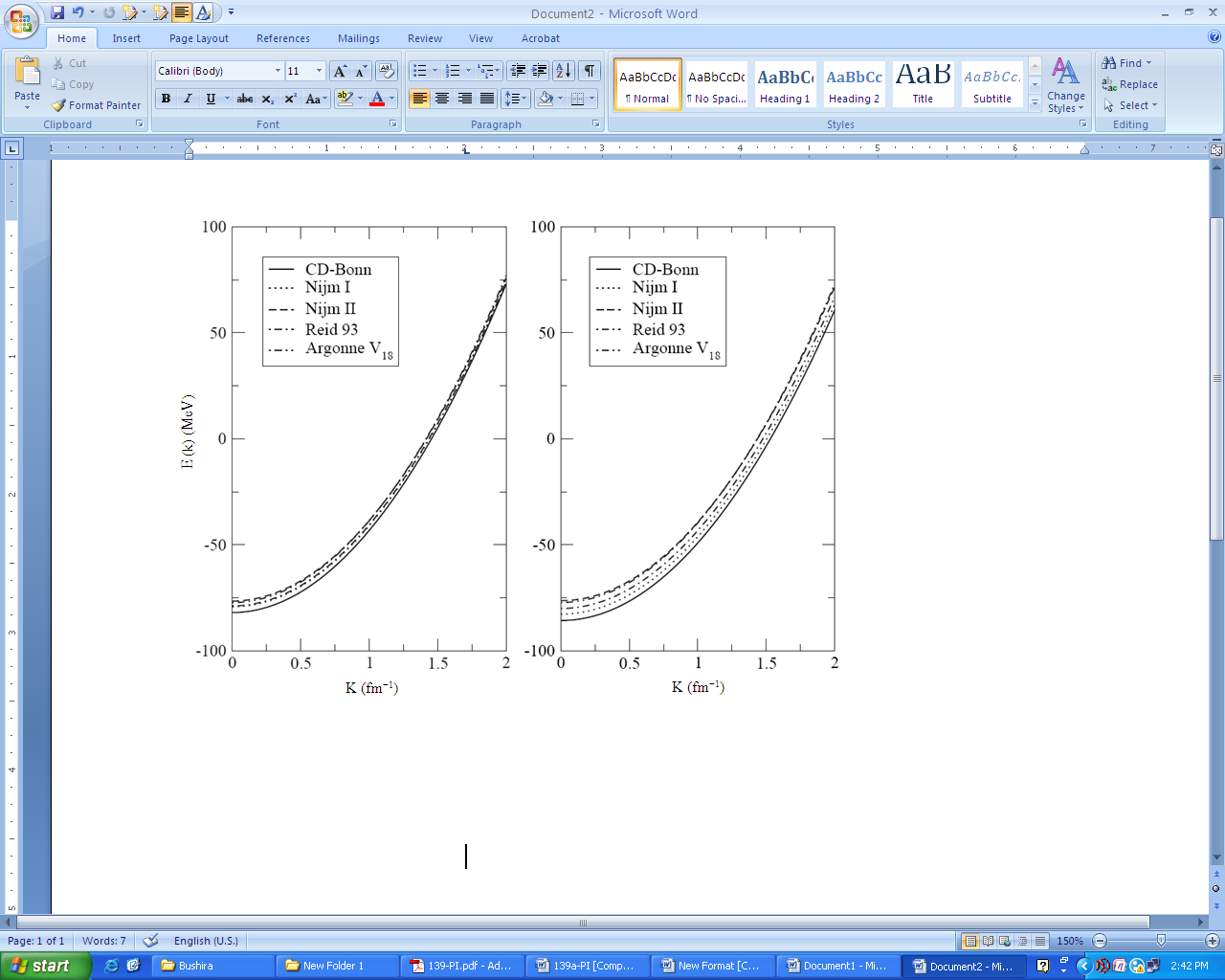
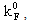 saturation energy EA, symmetry energy Esym, incompressibility K and effective mass m*/m. All results are calculated within BHF approach using the conventional (first group) and continuous (second group) choice for the auxiliary potential
saturation energy EA, symmetry energy Esym, incompressibility K and effective mass m*/m. All results are calculated within BHF approach using the conventional (first group) and continuous (second group) choice for the auxiliary potential