Adie. D. Salman1, Nadia. M. Adeeb1, Mohannad. H. Oleiwi2
1Department of Physics, College of Science, University of Karbala, Iraq
2Department of Physics, College of Education, University of Babylon, Iraq
Correspondence to: Nadia. M. Adeeb, Department of Physics, College of Science, University of Karbala, Iraq.
| Email: |  |
Copyright © 2012 Scientific & Academic Publishing. All Rights Reserved.
Abstract
The form factors for the inelastic electron scattering to 2+,4+ states in 46,48,50Ti are studied in the framework of shell model. The calculation is performed in (0f7/2,1p3/2,0f5/2,1p1/2) model space as well as extended 6ħω model space. The predictions of longitudinal form factors which includes core-polarization effects to first order were compared with the experimental values. It is noticed that the core polarization effects are essential in obtaining a remarkable agreement between the calculated inelastic longitudinal F(q)'s and those of experimental data.
Keywords:
Nuclear Reactions, Electron Scattering(E,E'), Inelastic Form Factors with Core-Polarization Effects
Cite this paper: Adie. D. Salman, Nadia. M. Adeeb, Mohannad. H. Oleiwi, Core Polarization Effects on the Inelastic Longitudinal C2 and C4 form Factors of 46,48,50 Ti Nuclei, Journal of Nuclear and Particle Physics, Vol. 3 No. 1, 2013, pp. 20-24. doi: 10.5923/j.jnpp.20130301.04.
1. Introduction
The calculations of Shell model, carried out within a model space in which the nucleon are restricted to occupy a few orbits are unable to reproduce the measured static moments or transition strengths without scaling factors. Comparison between calculated and measured longitudinal electron scattering form factors has long been used as stringent tests of models for transition densities. Various microscopic and macroscopic theories have been used to study excitations in nuclei[1]. Shell model within a restricted model space is one of the models, which succeeded in describing static properties of nuclei, when effective charges are used. Calculations of form factors using the model space wave function alone is inadequate for reproducing the data of electron scattering[2]. Therefore, effects out of the model space, which are called core polarization effects, are necessary to be included in the calculations. The intermediate one-particle one-hole states are taken up to 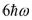 excitation. These effects are found essential for obtaining a quantitative agreement with the experimental data[3,4]. A microscopic model[5,6] has been used in order to study the core polarization effect on the longitudinal form factors of fp-shell nuclei. A microscopic model which adopted the first order core polarization was considered to calculate the C2 form factors of the fp-shell nuclei. Inelastic Electron Scattering from fp Shell Nuclei had been studied by Sahu et al[7]. They calculated form factors for
excitation. These effects are found essential for obtaining a quantitative agreement with the experimental data[3,4]. A microscopic model[5,6] has been used in order to study the core polarization effect on the longitudinal form factors of fp-shell nuclei. A microscopic model which adopted the first order core polarization was considered to calculate the C2 form factors of the fp-shell nuclei. Inelastic Electron Scattering from fp Shell Nuclei had been studied by Sahu et al[7]. They calculated form factors for 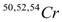 ,
, 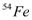 ,
, 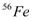 ,
, 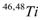 , and
, and 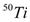 by the use of Hartree-Fock theory, results are in a good agreement with the experimental data. The form factors for the inelastic electron scattering to
by the use of Hartree-Fock theory, results are in a good agreement with the experimental data. The form factors for the inelastic electron scattering to 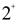 ,
, 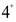 and
and 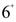 states in
states in 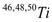 ,
, 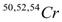 and
and 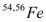 were studied by Sahu[8,9] in the framework of the Hartree-Fock model, also the calculation is performed in the 1f7/2, 2p3/2, 1f5/2, 2p1/2 model space using a modified Kuo-Brown effective interaction. Magnetic dipole excitation of N = 28 isotones
were studied by Sahu[8,9] in the framework of the Hartree-Fock model, also the calculation is performed in the 1f7/2, 2p3/2, 1f5/2, 2p1/2 model space using a modified Kuo-Brown effective interaction. Magnetic dipole excitation of N = 28 isotones 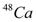 ,
, 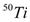 ,
, 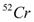 ,
, 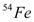 and
and 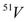 , was studied by Muto and Horie[10], in terms of the shell model by assuming
, was studied by Muto and Horie[10], in terms of the shell model by assuming 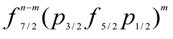 configurations with m = 0, 1 and 2 on an inert
configurations with m = 0, 1 and 2 on an inert 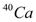 core.Coulomb form factors for the 0gnd+→2+ transitions in the even-even 1f7/2-shell nuclei are studied in terms of the shell model within the f7/2n+f7/2n-1p3/2 configurations and with the effective interactions. It is shown that the characteristics of the C2 form factors in the higher-momentum-transfer region, not explained by the simple f7/2n model, can be interpreted by the mixing of the one-particle excitations into the p3/2 orbit in the shell-model wave functions. E2 transition strengths and Q moments are also discussed in connection with the C2 form factors[11]. The use of modern realistic M3Y effective nucleon- nucleon interaction with two sets of fitting parameters (Ried fitting (M3Y-P1), and Paris fitting (M3Y-P0)) beside the use of MSDI has been done as a residual interactions within the calculation of core polarization effects in Inelastic longitudinal electron scattering C6 form factor in Ti-50 within the framework of first order perturbation theory (microscopic theory) with 2ћω excitation energy coupling the core orbits to the higher configurations one across the model space at normal transition. Harmonic oscillator wave functions (H.O) has been adopted as a single particle wave functions in 1f7/2 and with the aid of F7MBZ model space 1f7/2 effective interaction to generate the model space wave functions. The present results have been compared with the experimental data[12]. Differential cross sections for inelastic electron scattering from 40Ca, 42Ca, 44Ca, 46Ti, 48Ti, 50Ti and 56Fe have been measured. The cross sections for the strongly excited 2+, 3−, 4+ and 5− levels have been measured over a range of momentum transfer q of 0.4−2.6 fm−1. The data have been fitted using two representations for the transition charge, (i) the hydrodynamic liquid drop, and (ii) a phenomenological model[13].The aim of present work is to use a realistic effective nucleon-nucleon (NN) interaction as a residual interaction to calculate the core polarization (CP) effects through a microscopic theory, with a selection of model space effective interaction which generates the model space wave functions(shell model wave functions) and highly excited states. The (MSDI) were used in this case as a residual interaction. The strength of the MSDI denoted by AT ,B and C are set equal to A0=A1=B= 6.2 MeV and C=0. The single particle wave function were those of the harmonic oscillator potential (HO) with size parameter b chosen to reproduce the measured ground state root mean square charge radii of these nuclei. The one-body density matrix (OBDM) elements (
core.Coulomb form factors for the 0gnd+→2+ transitions in the even-even 1f7/2-shell nuclei are studied in terms of the shell model within the f7/2n+f7/2n-1p3/2 configurations and with the effective interactions. It is shown that the characteristics of the C2 form factors in the higher-momentum-transfer region, not explained by the simple f7/2n model, can be interpreted by the mixing of the one-particle excitations into the p3/2 orbit in the shell-model wave functions. E2 transition strengths and Q moments are also discussed in connection with the C2 form factors[11]. The use of modern realistic M3Y effective nucleon- nucleon interaction with two sets of fitting parameters (Ried fitting (M3Y-P1), and Paris fitting (M3Y-P0)) beside the use of MSDI has been done as a residual interactions within the calculation of core polarization effects in Inelastic longitudinal electron scattering C6 form factor in Ti-50 within the framework of first order perturbation theory (microscopic theory) with 2ћω excitation energy coupling the core orbits to the higher configurations one across the model space at normal transition. Harmonic oscillator wave functions (H.O) has been adopted as a single particle wave functions in 1f7/2 and with the aid of F7MBZ model space 1f7/2 effective interaction to generate the model space wave functions. The present results have been compared with the experimental data[12]. Differential cross sections for inelastic electron scattering from 40Ca, 42Ca, 44Ca, 46Ti, 48Ti, 50Ti and 56Fe have been measured. The cross sections for the strongly excited 2+, 3−, 4+ and 5− levels have been measured over a range of momentum transfer q of 0.4−2.6 fm−1. The data have been fitted using two representations for the transition charge, (i) the hydrodynamic liquid drop, and (ii) a phenomenological model[13].The aim of present work is to use a realistic effective nucleon-nucleon (NN) interaction as a residual interaction to calculate the core polarization (CP) effects through a microscopic theory, with a selection of model space effective interaction which generates the model space wave functions(shell model wave functions) and highly excited states. The (MSDI) were used in this case as a residual interaction. The strength of the MSDI denoted by AT ,B and C are set equal to A0=A1=B= 6.2 MeV and C=0. The single particle wave function were those of the harmonic oscillator potential (HO) with size parameter b chosen to reproduce the measured ground state root mean square charge radii of these nuclei. The one-body density matrix (OBDM) elements (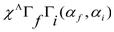 ) are calculated using the shell model code OXBASH[14]
) are calculated using the shell model code OXBASH[14]
2. Theory
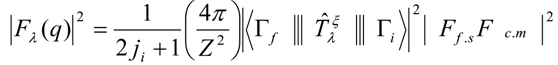 | (1) |
Where 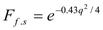 is the finite nucleon-size correction and
is the finite nucleon-size correction and 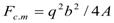 is the center of mass correction,
is the center of mass correction, 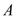 is the mass number and b is the harmonic oscillator size parameter.The effect of the core polarization on the form factors is based on a microscopic theory, which combines shell-model wave functions and configuration with higher energy as particle-hole perturbation expansion. The reduced matrix element of the electron scattering operator
is the mass number and b is the harmonic oscillator size parameter.The effect of the core polarization on the form factors is based on a microscopic theory, which combines shell-model wave functions and configuration with higher energy as particle-hole perturbation expansion. The reduced matrix element of the electron scattering operator 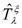 is expressed as a sum of the fp-model space (p) contribution and the core-polarization (cp) contribution, as follows[5].
is expressed as a sum of the fp-model space (p) contribution and the core-polarization (cp) contribution, as follows[5]. 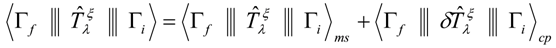 | (2) |
selection the longitudinal (L), electric(E) and magnetic(M) transverse form factors , The Greek symbol were used to denote quantum numbers in coordinate space ,and isospace and isospace respectively: 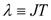
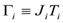
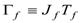 where The fp-shell model space element can be expressed as linear combination of the single-particle matrix element[16] .
where The fp-shell model space element can be expressed as linear combination of the single-particle matrix element[16] .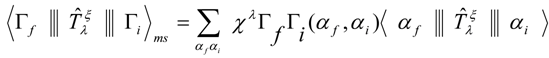 | (3) |
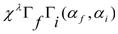 where the structure factors (one body density matrix element), given by,
where the structure factors (one body density matrix element), given by,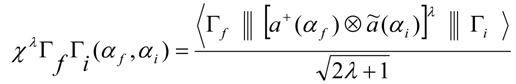 | (4) |
are the single-particle states 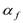 and
and 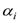 for the fp-shell model space. Similarly, core-polarization matrix element as follow:
for the fp-shell model space. Similarly, core-polarization matrix element as follow: 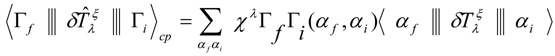 | (5) |
Up to the first order perturbation theory, the single-particle matrix element for the higher-energy configuration is given by[17] 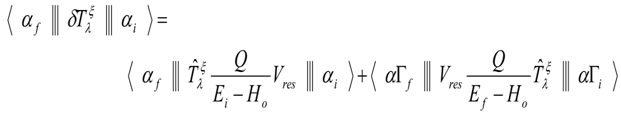 | (6) |
The operator Q is the projection operator on the space outside the model space. 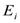 and
and 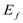 are the energies of initial and final states. For the residual interaction
are the energies of initial and final states. For the residual interaction 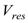 the MSDI and M3Y were adopted.The two terms in right hand side of Eq.(6) can be written as[18]
the MSDI and M3Y were adopted.The two terms in right hand side of Eq.(6) can be written as[18] 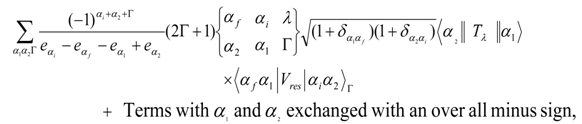 | (7) |
runs over particle hole states 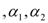 whereand (e) is the single-particle energy.
whereand (e) is the single-particle energy.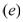 and
and 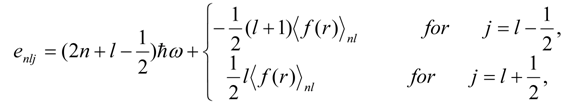 | (8) |
With 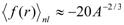 and
and 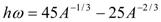 The electric transition strength is given by,
The electric transition strength is given by,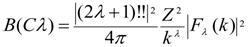 | (9) |
Where k = Ex /ћc .
3. Results and Discussion
The core polarization effect(cp) are calculated with the MSDI as residual interaction. The parameters of MSDI are denoted by AT , B and C. where T indicates the isospin (0,1). These parameters are taken to be A0=A1=B= 6.2MeV and C=0. In all of the following diagrams the dashed line give the results obtained using the fp-shell wave function and the results including cp effects are shown by solid curve.
3.1. Form Factors for the 0+ to 2+ Transition
A comparison between the experimental and theoretical form factors for the C2 transition for 46,48,50Ti is given in figures(1 - 3) respectively. For each of these three nuclei, the form factors shows three peaks. Figure (1) shows longitudinal C2 electron scattering form factors as s function of momentum transfer for 46Ti. We observed that the first peak occur at q=0.7fm-1,the second at=1.5 fm-1 and the third peak at=2.5fm-1. It is noticed from figure.(1) that the inclusion of cp enhance the C2 form factor. This enhancement brings the total form factors very close to the experimental data for the first peak q<1fm-1, while the second and third peak are overestimated. We notice that from figure(1) the model space fail to describe the form factors in all momentum transfer. 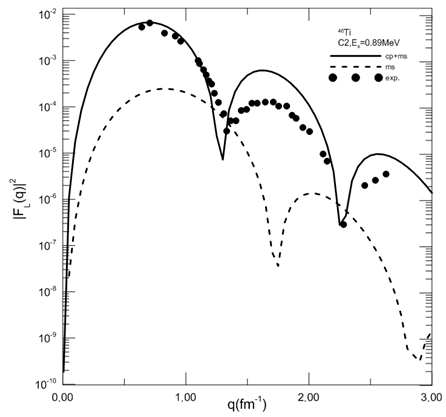 | Figure (1). Inelastic longitudinal form factors for the transition to the 2+ in the 46Ti,the experimental data are taken from ref.[8] |
Figure. (2) displays the calculation of the C2 form factors Jπ=2+,T=2 at Ex =0.98MeV for 48Ti. The first peak occur at=0.7fm-1 the second at = 1.7fm-1and the third peak at=3fm-1. The model space calculation fail to describe the form factors and the inclusion of the core polarization enhances the calculations and bring the form factors to the experimental values up to momentum transfer q=1fm-1,while the second peak is overestimated and the third peak is underestimated. Sahu et. al[8] have quite successfully reproduced the first two peaks where we get similar results for the first and third peaks.Figure(3) displays the calculation of the C2 form factors to the Jπ=2+,T=3 at Ex=1.55MeV for 50Ti. We observe three peaks, the first peak occur at q=0.7fm-1 the second at q=1.7fm-1 and the third peak at q=3fm-1. We notice that the model space calculation fail to describe the form factors in all momentum transfer region. The (cp) effects enhance the C2 form factors in all momentum transfer, where we notice that the results of cp effects give good agreement with exp. data especially ,for the first peak up to q=1.3fm-1, while the second peak is overestimated and the third peak is underestimated. Sahu et. al[8] observe two peaks and have quite successfully reproduced the first peak, but the second peak is underestimated and they fail to reproduced the third peak. However the results for the second and third peaks in 50Ti are better in our calculations. The three figures show that the first region of angular momentum gives agood agreement for (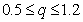 ) by using the core polarization effects ,where the results at(
) by using the core polarization effects ,where the results at(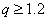 ) need more modification to get agood agreement with the experimental data.
) need more modification to get agood agreement with the experimental data.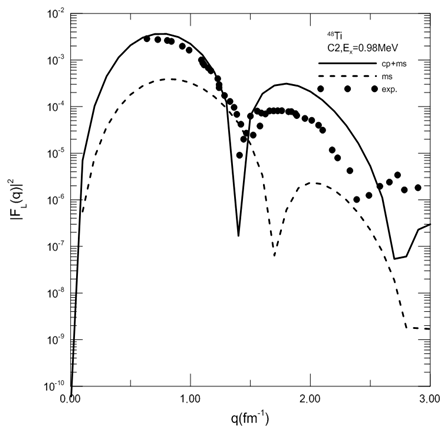 | Figure (2). Inelastic longitudinal form factors for the transition to the 2+ in the 48Ti,the experimental data are taken from ref.[8] |
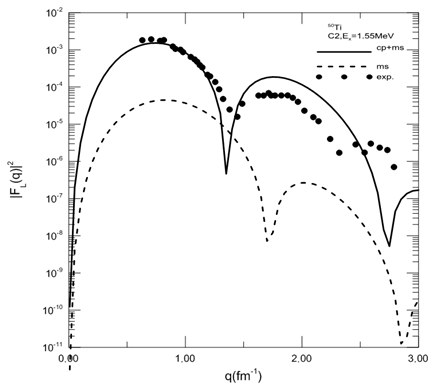 | Figure (3). Inelastic longitudinal form factors for the transition to the 2+ in the 50Ti the experimental data are taken from ref.[8] |
3.2. Form Factors for the 0+ to 4+ Transition
Figure (4) compare the calculated and experimental of longitudinal C4 form factors for 48Ti at Ex=1.967MeV. The model space calculation underestimates the exp. and the inclusion of cp enhances the calculations. It is seen that the present calculation is quite successful in reproducing the magnitude of the form factors at the first maximum. However one observes discrepancies in the momentum transfer range 1.3 < q<1.8. 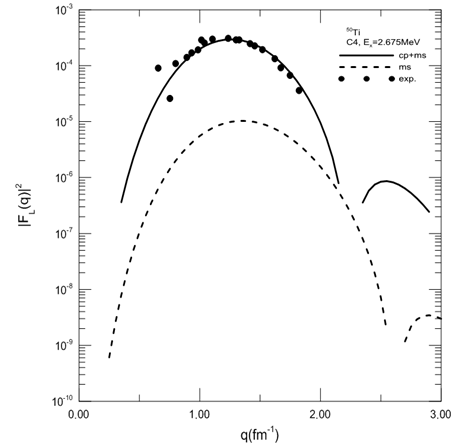 | Figure (4). Inelastic longitudinal form factors for the transition to the 4+ in the 48Ti ,the experimental data are taken from ref. [19] |
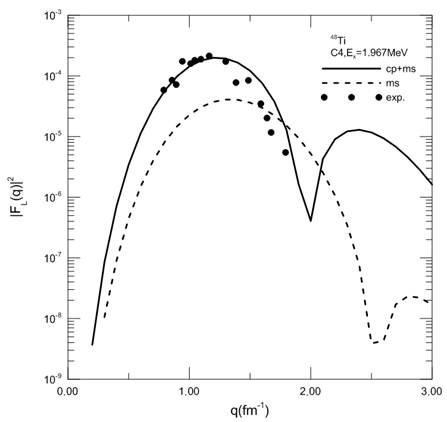 | Figure (5). Inelastic longitudinal form factors for the transition to the 4+ in the 50Ti, the experimental data are taken from ref.[19] |
Raina et al[19] were unable to reproduced the first maximum within their projected Hatree-Fock-Bogoliubov formalism even they have changed the effective charges from one nucleus to another, where we are get a better results. Figure(5) displays the calculation of the C4 form factors to the Jπ=4+ T=3 at Ex=2.675MeV. The cp effects enhance the C4 form factors and the model space fail to describe the data in the form factors as shown by dashed curve. The results of the fp-shell model space with cp effects give good agreement with the exp. data. Raina et al[19] have quite successfully reproduced the first peak in term of shell model within their HFB formalism. However the results of the first peak are better in our calculation. In these two transitions for 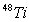 and
and 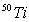 the effects of core-polarization shows is clear in figure(4) than figure(5) which need more corrections to get agood results.
the effects of core-polarization shows is clear in figure(4) than figure(5) which need more corrections to get agood results.
4. Conclusions
The fp-shell models, which can describe static properties and energy level are less successful in describing dynamic properties such as C2 and C4 transition rates and electron scattering form factors. The inclusion of higher-excited configurations by means of (cp) enhances the form factors and brings the theoretical results closer to the experimental data.
ACKNOWLEDGMENTS
Authors would like to express their thanks to prof. B.A.Brown of the national superconducting cyclotron laboratory, Michigan state University for providing him computer code OXBASH[11]. We would like to express our thank to our teacher Prof. Dr.Raad.A.Radhi of the department of physics ,college of science at the university of Baghdad for providing him the computer cods written in Fortran 90 language
References
| [1] | T. Sato, K. Koshigiri and H. Ohtsubos: Z. Phys., A320 (1985) 507 . |
| [2] | J. G. L. Booten and A. G. M. Van Hees:" Nucl. Phys. A569 (1994) 510. |
| [3] | A. Yokoyama and K. Ogawa; Phys. Rev. C39(1989)2458. |
| [4] | T. Sato, N. Odagawa, H. Ohtsubo, T. S. H. Lee, Phys. Rev. C49(1994) 776. |
| [5] | R.A. Radhil, A. A. Abdullah, Z. A. Dakhil, N. M. Adeeb, Nucl. Phys. A696(2001) 442. |
| [6] | R.A. Radhi, Nucl. Phys. A716(2003)100. |
| [7] | R. Sahu, D. P. Ahalpara and K. H. Bhatt,[Bull.Am.Phys.Soc. 31, No.10, 1764, DC7 (1986)]. |
| [8] | R. Sahu, D. P. Ahalpara and K. H. Bhatt, J. Phys. (London) G16, 733 (1990). |
| [9] | R. Sahu, D. P. Ahalpara and S. P. Pandya, J. Phys. (London) G13, 603 (1987). |
| [10] | K. Muto and H. Horie, Nucl. Phys. A440, 254 (1985). |
| [11] | T.Iwamoto ,H.Horie and A.Yokoyama,phys. Rev.C, Vol.25, 658 (1982). |
| [12] | F.Z. Majeed , N.M.Adeeb,A.A.Qassim, Iraqi Journal of Science,Vol.53,No.3,564(2012). |
| [13] | J.Heisenberg, J.S.McCarthy, I.Sick, Nucl.phys.A,Vol.164, 353 (1971) |
| [14] | B.A. Brown, A. Etchegoyen, N.S. Godwin,W.D.M. Rae, W.A. Richter, W.E. Ormand, E.K. Warburton, J.S. Winfield, L. Zhao and C.H. Zimmerman, MSU-NSCL report number 1289. particle and nuclear physics,47,517,(2001) |
| [15] | T.de Forest, jr and J. d. Walecka, Adv. Phys. 15(1966)1. |
| [16] | B.H.Wildenthal; Prog Part Nucl.Phys,11(1984)5. |
| [17] | P.J. Ellis and H.A. Mavromattes; Nucl. Phys.A175(1971)309. |
| [18] | P.J. Brussaard, P.W.M. Glaudemans, "Shell Model Application in Nuclear Spectroscopy", North-Holland, Amsterdam (1977). |
| [19] | P. K. Raina and S. K. Sharma, Phys. Rev. C37(1988) 1427. |

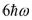 excitation. These effects are found essential for obtaining a quantitative agreement with the experimental data[3,4]. A microscopic model[5,6] has been used in order to study the core polarization effect on the longitudinal form factors of fp-shell nuclei. A microscopic model which adopted the first order core polarization was considered to calculate the C2 form factors of the fp-shell nuclei. Inelastic Electron Scattering from fp Shell Nuclei had been studied by Sahu et al[7]. They calculated form factors for
excitation. These effects are found essential for obtaining a quantitative agreement with the experimental data[3,4]. A microscopic model[5,6] has been used in order to study the core polarization effect on the longitudinal form factors of fp-shell nuclei. A microscopic model which adopted the first order core polarization was considered to calculate the C2 form factors of the fp-shell nuclei. Inelastic Electron Scattering from fp Shell Nuclei had been studied by Sahu et al[7]. They calculated form factors for 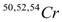 ,
, 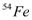 ,
, 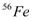 ,
, 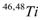 , and
, and 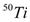 by the use of Hartree-Fock theory, results are in a good agreement with the experimental data. The form factors for the inelastic electron scattering to
by the use of Hartree-Fock theory, results are in a good agreement with the experimental data. The form factors for the inelastic electron scattering to 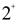 ,
, 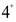 and
and 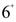 states in
states in 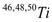 ,
, 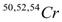 and
and 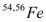 were studied by Sahu[8,9] in the framework of the Hartree-Fock model, also the calculation is performed in the 1f7/2, 2p3/2, 1f5/2, 2p1/2 model space using a modified Kuo-Brown effective interaction. Magnetic dipole excitation of N = 28 isotones
were studied by Sahu[8,9] in the framework of the Hartree-Fock model, also the calculation is performed in the 1f7/2, 2p3/2, 1f5/2, 2p1/2 model space using a modified Kuo-Brown effective interaction. Magnetic dipole excitation of N = 28 isotones 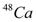 ,
, 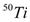 ,
, 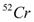 ,
, 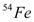 and
and 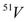 , was studied by Muto and Horie[10], in terms of the shell model by assuming
, was studied by Muto and Horie[10], in terms of the shell model by assuming 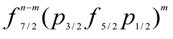 configurations with m = 0, 1 and 2 on an inert
configurations with m = 0, 1 and 2 on an inert 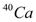 core.Coulomb form factors for the 0gnd+→2+ transitions in the even-even 1f7/2-shell nuclei are studied in terms of the shell model within the f7/2n+f7/2n-1p3/2 configurations and with the effective interactions. It is shown that the characteristics of the C2 form factors in the higher-momentum-transfer region, not explained by the simple f7/2n model, can be interpreted by the mixing of the one-particle excitations into the p3/2 orbit in the shell-model wave functions. E2 transition strengths and Q moments are also discussed in connection with the C2 form factors[11]. The use of modern realistic M3Y effective nucleon- nucleon interaction with two sets of fitting parameters (Ried fitting (M3Y-P1), and Paris fitting (M3Y-P0)) beside the use of MSDI has been done as a residual interactions within the calculation of core polarization effects in Inelastic longitudinal electron scattering C6 form factor in Ti-50 within the framework of first order perturbation theory (microscopic theory) with 2ћω excitation energy coupling the core orbits to the higher configurations one across the model space at normal transition. Harmonic oscillator wave functions (H.O) has been adopted as a single particle wave functions in 1f7/2 and with the aid of F7MBZ model space 1f7/2 effective interaction to generate the model space wave functions. The present results have been compared with the experimental data[12]. Differential cross sections for inelastic electron scattering from 40Ca, 42Ca, 44Ca, 46Ti, 48Ti, 50Ti and 56Fe have been measured. The cross sections for the strongly excited 2+, 3−, 4+ and 5− levels have been measured over a range of momentum transfer q of 0.4−2.6 fm−1. The data have been fitted using two representations for the transition charge, (i) the hydrodynamic liquid drop, and (ii) a phenomenological model[13].The aim of present work is to use a realistic effective nucleon-nucleon (NN) interaction as a residual interaction to calculate the core polarization (CP) effects through a microscopic theory, with a selection of model space effective interaction which generates the model space wave functions(shell model wave functions) and highly excited states. The (MSDI) were used in this case as a residual interaction. The strength of the MSDI denoted by AT ,B and C are set equal to A0=A1=B= 6.2 MeV and C=0. The single particle wave function were those of the harmonic oscillator potential (HO) with size parameter b chosen to reproduce the measured ground state root mean square charge radii of these nuclei. The one-body density matrix (OBDM) elements (
core.Coulomb form factors for the 0gnd+→2+ transitions in the even-even 1f7/2-shell nuclei are studied in terms of the shell model within the f7/2n+f7/2n-1p3/2 configurations and with the effective interactions. It is shown that the characteristics of the C2 form factors in the higher-momentum-transfer region, not explained by the simple f7/2n model, can be interpreted by the mixing of the one-particle excitations into the p3/2 orbit in the shell-model wave functions. E2 transition strengths and Q moments are also discussed in connection with the C2 form factors[11]. The use of modern realistic M3Y effective nucleon- nucleon interaction with two sets of fitting parameters (Ried fitting (M3Y-P1), and Paris fitting (M3Y-P0)) beside the use of MSDI has been done as a residual interactions within the calculation of core polarization effects in Inelastic longitudinal electron scattering C6 form factor in Ti-50 within the framework of first order perturbation theory (microscopic theory) with 2ћω excitation energy coupling the core orbits to the higher configurations one across the model space at normal transition. Harmonic oscillator wave functions (H.O) has been adopted as a single particle wave functions in 1f7/2 and with the aid of F7MBZ model space 1f7/2 effective interaction to generate the model space wave functions. The present results have been compared with the experimental data[12]. Differential cross sections for inelastic electron scattering from 40Ca, 42Ca, 44Ca, 46Ti, 48Ti, 50Ti and 56Fe have been measured. The cross sections for the strongly excited 2+, 3−, 4+ and 5− levels have been measured over a range of momentum transfer q of 0.4−2.6 fm−1. The data have been fitted using two representations for the transition charge, (i) the hydrodynamic liquid drop, and (ii) a phenomenological model[13].The aim of present work is to use a realistic effective nucleon-nucleon (NN) interaction as a residual interaction to calculate the core polarization (CP) effects through a microscopic theory, with a selection of model space effective interaction which generates the model space wave functions(shell model wave functions) and highly excited states. The (MSDI) were used in this case as a residual interaction. The strength of the MSDI denoted by AT ,B and C are set equal to A0=A1=B= 6.2 MeV and C=0. The single particle wave function were those of the harmonic oscillator potential (HO) with size parameter b chosen to reproduce the measured ground state root mean square charge radii of these nuclei. The one-body density matrix (OBDM) elements (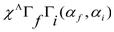 ) are calculated using the shell model code OXBASH[14]
) are calculated using the shell model code OXBASH[14]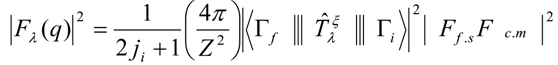
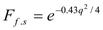 is the finite nucleon-size correction and
is the finite nucleon-size correction and 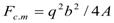 is the center of mass correction,
is the center of mass correction, 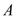 is the mass number and b is the harmonic oscillator size parameter.The effect of the core polarization on the form factors is based on a microscopic theory, which combines shell-model wave functions and configuration with higher energy as particle-hole perturbation expansion. The reduced matrix element of the electron scattering operator
is the mass number and b is the harmonic oscillator size parameter.The effect of the core polarization on the form factors is based on a microscopic theory, which combines shell-model wave functions and configuration with higher energy as particle-hole perturbation expansion. The reduced matrix element of the electron scattering operator  is expressed as a sum of the fp-model space (p) contribution and the core-polarization (cp) contribution, as follows[5].
is expressed as a sum of the fp-model space (p) contribution and the core-polarization (cp) contribution, as follows[5]. 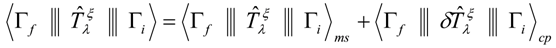
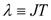
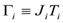
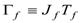 where The fp-shell model space element can be expressed as linear combination of the single-particle matrix element[16] .
where The fp-shell model space element can be expressed as linear combination of the single-particle matrix element[16] .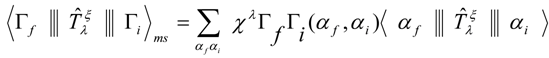
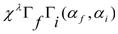 where the structure factors (one body density matrix element), given by,
where the structure factors (one body density matrix element), given by,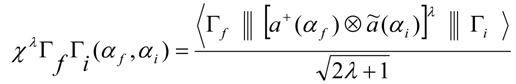
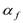 and
and 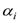 for the fp-shell model space. Similarly, core-polarization matrix element as follow:
for the fp-shell model space. Similarly, core-polarization matrix element as follow: 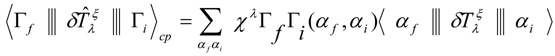
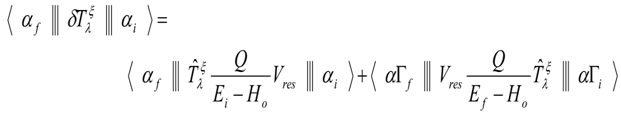
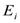 and
and 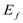 are the energies of initial and final states. For the residual interaction
are the energies of initial and final states. For the residual interaction 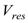 the MSDI and M3Y were adopted.The two terms in right hand side of Eq.(6) can be written as[18]
the MSDI and M3Y were adopted.The two terms in right hand side of Eq.(6) can be written as[18] 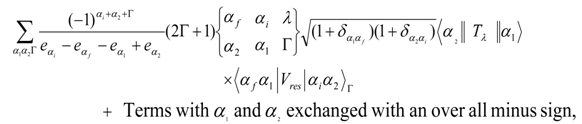
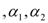 whereand (e) is the single-particle energy.
whereand (e) is the single-particle energy.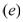 and
and 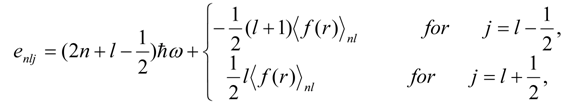
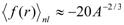 and
and 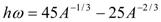 The electric transition strength is given by,
The electric transition strength is given by,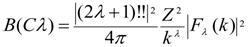

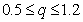 ) by using the core polarization effects ,where the results at(
) by using the core polarization effects ,where the results at( ) need more modification to get agood agreement with the experimental data.
) need more modification to get agood agreement with the experimental data.



 and
and 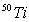 the effects of core-polarization shows is clear in figure(4) than figure(5) which need more corrections to get agood results.
the effects of core-polarization shows is clear in figure(4) than figure(5) which need more corrections to get agood results. Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML