1. Introduction

Measurements of the poloidal beta, plasma energy, plasma pressure, plasma temperature, plasma resistance, and plasma effective atomic number are essential for tokamak experiments and optimized operation. In recent year, penetration processes of the Rotating Helical Field (RHF) into tokamak plasmas have been investigated on a small tokamak device IR-T1. Magnetic diagnostics, in particular diamagnetic loop (toroidal flux loop) are commonly used in tokamaks to measure the variation of toroidal flux induced by the plasma or diamagnetic flux and then poloidal beta. Therefore the plasma pressure and energy which relate to poloidal Beta, obtained. On the other hand, the plasma resistance and plasma effective atomic number obtained using poloidal flux loop and Rogowski coil measurements. Also measurement of plasma energy with diamagnetic loop and measurement of plasma density with Langmuir probe gives a value of plasma temperature[1-56]. In this paper we describe experimental investigation of effects of Rotating Helical Field (RHF) (RHF is an external helical magnetic field which can improve the tokamak plasma confinement) on measurements of these parameters on IR-T1 tokamak, which it is a small, low beta, and large aspect ratio tokamak with a circular cross section. Theoretical approach for measurement of these parameters will present in section 2. Resonant Helical Field (RHF) setup on IR-T1 tokamak will be presented in section 3. Experimental results of effects of RHF on measurements of parameters will be presented in section 4. Summary and conclusion are also will be presented in section 5.

2. Measurements of Plasma Parameters Based on Diamagnetic Effect

Diamagnetic loop measure the toroidal diamagnetic flux for the purposes of measurements of the plasma parameters e.g. poloidal beta, plasma pressure, and thermal energy of the plasma. The toroidal flux that produced by the plasma is related to the total perpendicular thermal energy of the plasma. This diamagnetic flux is usually measured with the diamagnetic loop. Relation between the diamagnetic flux and the poloidal beta derived from simplified equilibrium relation[3,6,7]:

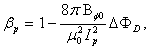(1)

where

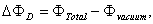and ,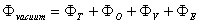

and where 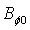is the toroidal magnetic field in the absence of the plasma which can be obtained by the magnetic probe, 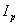is the plasma current which can be obtained by the Rogowski coil, 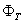is the toroidal flux because of toroidal field coils, 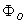and 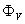are the passing flux through loop due to possible misalignment between ohmic field and vertical field and the diamagnetic loop and 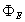is the toroidal field due to eddy current on the vacuum chamber. These fluxes can be compensated either with compensation coil or fields discharge without plasma. It must be noted that compensating coil for diamagnetic loop is wrapped out of the plasma current, and only the toroidal flux (which is induced by the change of toroidal field coil current when plasma discharges) can be received. The diamagnetic loop signal contains two parts, plasma diamagnetic flux and the vacuum toroidal flux. So the diamagnetic flux 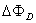caused by plasma current can be measured from the diamagnetic loop and compensating coil using subtraction.

If we want to have a determination of the volume averaged plasma kinetic pressure 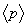, it is can be measured directly from the definition of the poloidal beta:

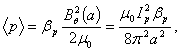(2)

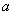where is the plasma minor radius.

In order to measurement of the plasma thermal energy we start from the plasma state equation:

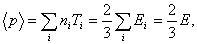(3)

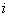where subscript indicate the plasma species , and 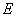indicate the plasma thermal energy density, therefore the plasma thermal energy 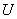, and also plasma temperature is obtained:

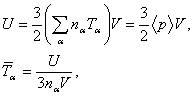(4)

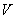where is the plasma volume. If we have the quasi neutral plasma density from the Langmuir probe measurements, then we can find the plasma averaged temperature from Eq. (4).

Moreover, the plasma specific resistance in the steady state plasma is can be written as:

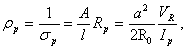(5)

where is the plasma conductivity, 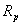is the plasma resistance, and 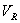is the resistive component of the loop voltage (poloidal flux loop). Also for determining the plasma effective atomic number we use the Spitzer relation for plasma conductivity[6]:

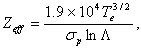(6)

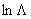where is the Coulomb logarithm.

Therefore according to above discussion we can find the mentioned parameters by the diamagnetic loop and with helping of the Rogowski coil, poloidal flux loop, and Langmuir probe measurements. Experimental results for determinations of these parameters will be presented in section 4.

3. Resonant Helical Field (RHF) Setup on IR-T1 tokamak

The RHF is an external helical magnetic field which can improve the tokamak plasma confinement. In the IR-T1, This field is produced by two winding with optimized geometry conductors wound externally around the tokamak chamber with a given helicity. The minor radius of these helical windings are 21cm (L=2, n=1) and 22cm (L=3, n=1) and also major radius is 50cm (see Fig. (1)). In this experiment, the current through the helical windings was between 200-300A, which is very low compared with the plasma current (32 kA).

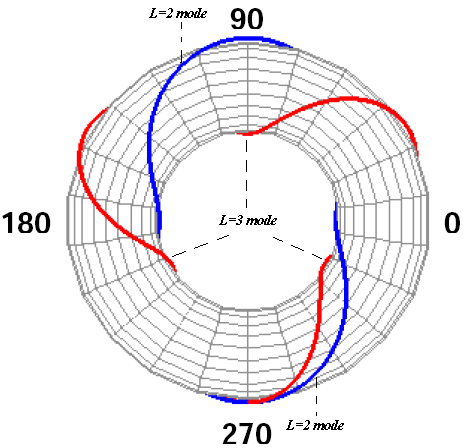Figure (1). Positions of the RHF coils (l=2 & L=3 modes) on outer surface of the IR-T1 tokamak chamber

4. Experimental Results

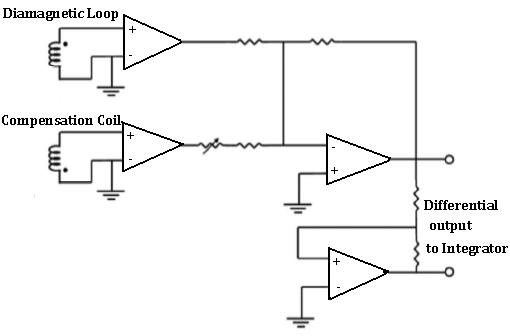Figure (2). Electric circuit used for diamagnetic loop and its compensation coil

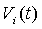We used the circuit as shown in Fig. (2), for the measurement of induced voltage in the diamagnetic loop:

The integrator output 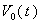of Fig. (2), is given by:

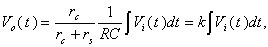(7)

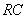where, is the integrator time constant and Eq. (7) is the integrated output of the loop signal. Moreover 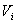is the inductive voltage supplied by the diamagnetic loop, where installed around the vacuum chamber of the IR-T1 tokamak.

Therefore, diamagnetic flux can be obtained from:

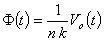(8)

Experimental results of effects of RHF on plasma parameters, present in Figures (3)-(10). As shown in these Figures, main results of effects of L=2 and L=3 modes are flatting the plasma current, pressure, energy, temperature, and effective atomic number profiles. In other words, the addition of a relatively small amount of RHF with L=2 and L=3 modes could be effective for improving the quality of tokamak plasma discharge by creating the steady state plasma.

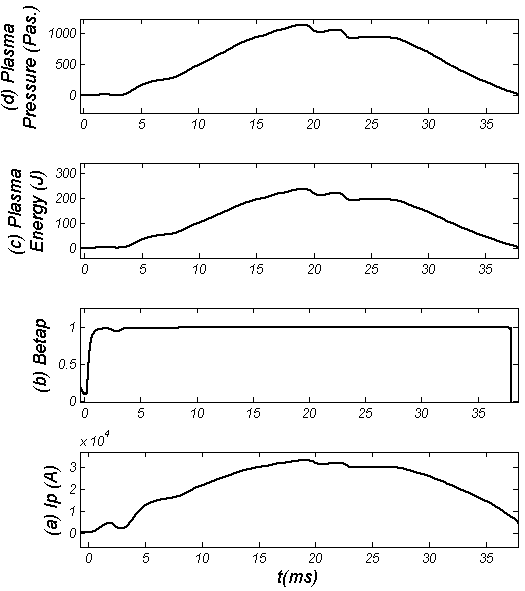Figure (3). Plasma parameters without RHF: (a) Plasma Current, (b) Poloidal beta, (c) Plasma energy, and (d) Plasma pressure

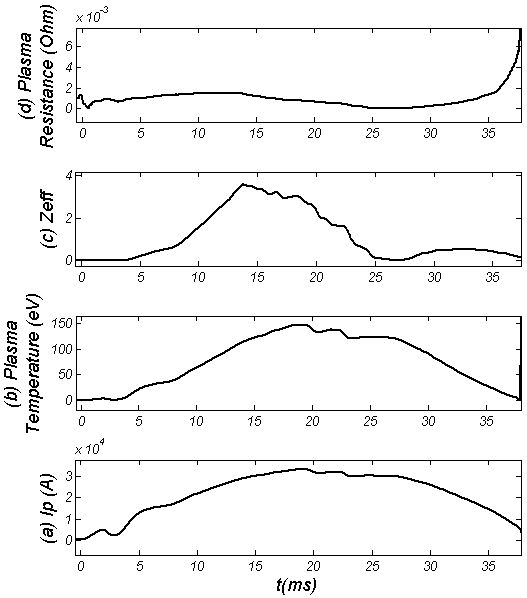Figure (4). Plasma parameters without RHF: (a) Plasma Current, (b) Plasma temperature, (c) Effective atomic number, and (d) Plasma resistance

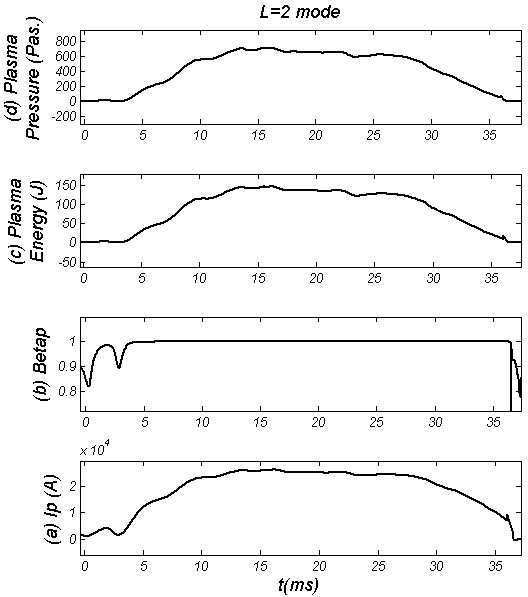Figure (5). Plasma parameters in presence of RHF (L=2 mode at 13-25ms): (a) Plasma Current, (b) Poloidal beta, (c) Plasma energy, and (d) Plasma pressure

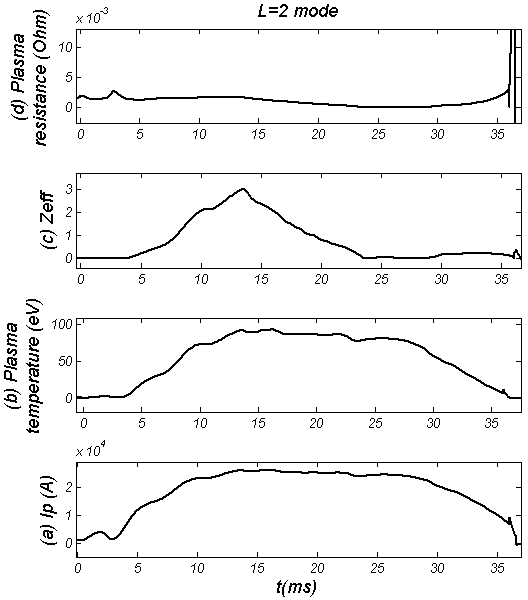Figure (6). Plasma parameters in presence of RHF (L=2 mode at 13-25ms): (a) Plasma Current, (b) Plasma temperature, (c) Effective atomic number, and (d) Plasma resistance

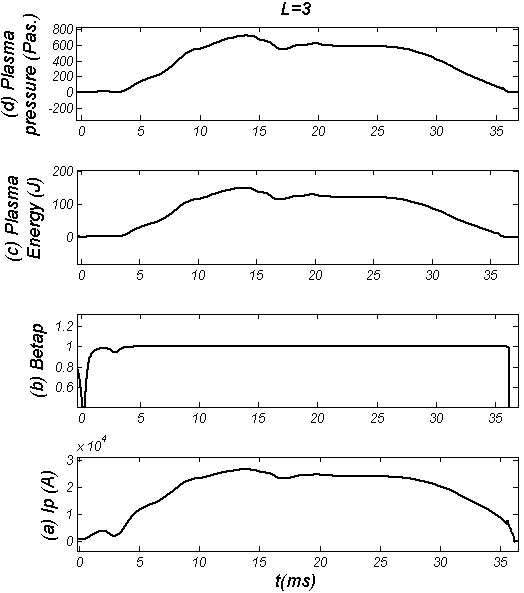Figure (7). Plasma parameters in presence of RHF (L=3 mode at 13-25ms): (a) Plasma Current, (b) Poloidal Beta, (c) Plasma energy, and (d) Plasma pressure

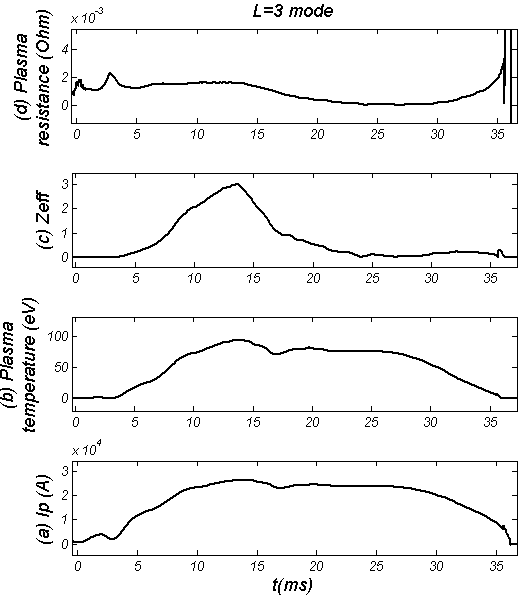Figure (8). Plasma parameters in presence of RHF (L=3 mode at 13-25ms): (a) Plasma Current, (b) Plasma temperature, (c) Effective atomic number, and (d) Plasma resistance

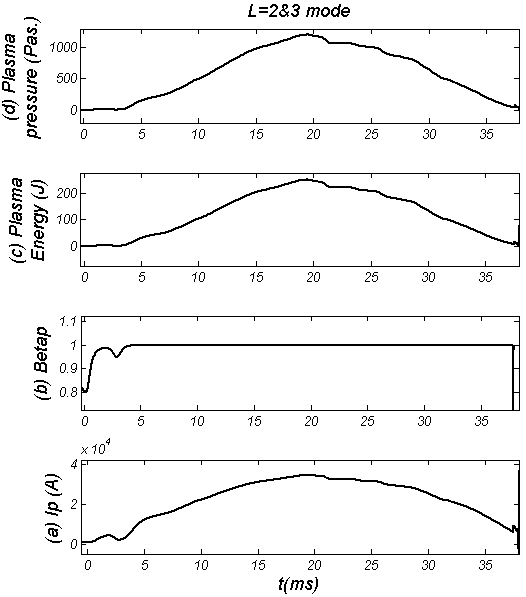Figure (9). Plasma parameters in presence of RHF (L=2&3 mode at 13-25ms): (a) Plasma Current, (b) Poloidal Beta, (c) Plasma energy, and (d) Plasma pressure

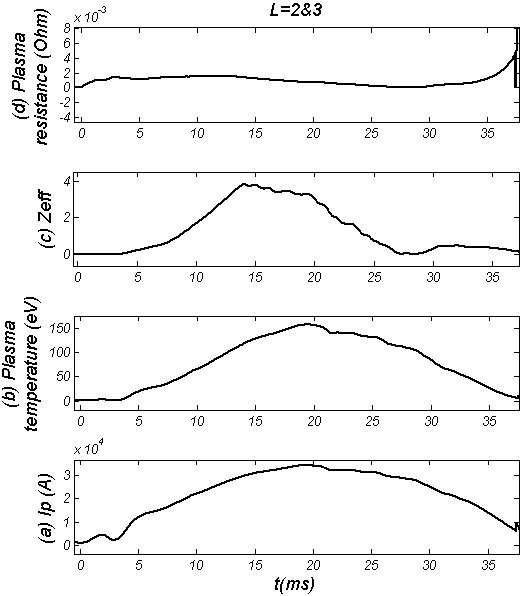Figure (10). Plasma parameters in presence of RHF (L=2&3 mode at 13-25ms): (a) Plasma Current, (b) Plasma temperature, (c) Effective atomic number, and (d) Plasma resistance

5. Summary and Conclusions

Determinations of poloidal beta, plasma energy, plasma pressure, plasma temperature, plasma resistance, and plasma effective atomic number are important in tokamak plasma experiments. In this paper we present an experimental investigation of effects of RHF on these parameters, especially based on toroidal flux loop in IR-T1 tokamak. For this purposes a diamagnetic loop with its compensation coil constructed and installed on outer surface of the IR-T1. Also in this work we measured the plasma current, plasma voltage, and the plasma density from the Rogowski coil, poloidal flux loop, and the Langmuir probe measurements, respectively. Experimental results of effects of RHF on plasma parameters, show that in cases of L=2 and L=3 modes, despite of little decreasing of plasma pressure and energy, the steady state plasma produced, which it is important in plasma equilibrium studies. But in case of L=2&3 mode, despite of very little flatting of profiles, the plasma pressure, temperature, and energy increased 3-5%. In other words, the addition of a relatively small amount of RHF with L=2 and L=3 modes could be effective for improving the quality of tokamak plasma discharge by creating the steady state plasma.