Oleg A. Teplov
Russian Academy of Science, Institute of Metallurgy and Materials Science, Moscow, 119991, Russia
Correspondence to: Oleg A. Teplov, Russian Academy of Science, Institute of Metallurgy and Materials Science, Moscow, 119991, Russia.
| Email: |  |
Copyright © 2012 Scientific & Academic Publishing. All Rights Reserved.
Abstract
The mass formation of basic vector mesons and quarkoniums up to energy 4.5 GeV was studied. The investigation was done with using of jet mechanism, the harmonic quarks and neutral colorless groups. The quark group with rest mass equal to experimental mass of hadron was named as flower. The quark flowers were found for ρ, ω, φ, b1(1235), φ(1680), ψ/J, ψ(2S), ψ(3770), ψ(4040) and ψ(4415). Flower and experimental masses of mesons within the limits of their experimental uncertainty completely coincide. Flower masses of ω and ψ(2S) were defined as 782.67 and 3686.09 MeV. The quark flowers of vector mesons of e+e−-annihilation are symmetrical and consist from an aura and central part. The formation of quark shells, the condensation of quarks on the quark leaders, complicated hadronization, acceptor properties of c-quark and the floral scheme of kaon formation are discussed.
Keywords:
Harmonic Quarks, Vector Mesons, Annihilation, Hadronization, Quark Condensation
Cite this paper: Oleg A. Teplov, Quark Flowers and Quark Condensation, Journal of Nuclear and Particle Physics, Vol. 3 No. 1, 2013, pp. 8-13. doi: 10.5923/j.jnpp.20130301.02.
1. Introduction
In[1],[2] was shown that the harmonic quarks[3] and their completed oscillators are the building blocks for the hadronic mass spectrum. These investigations were continued at the present paper. Their purpose is a search of the groups of harmonic quarks which are responsible for masses of the observed vector mesons in the e+e−-annihilation up to energy 4.5 GeV. Only harmonic quarks, as the constituent quarks of hadrons and especially exact instrument, can be using for like investigations. At e+e−-annihilation, as a result of an electromagnetic interaction, there will be generated the intermediate virtual photon which then decays upon a lepton pair or a quark-antiquark pair. An initial quark and an antiquark (quark leaders) should possess high momentums, but presence of color charges do not allow to exist it in loneliness and so the quarks fly away together with necessary entourage which it capture from physical vacuum. Thus two jets of hadrons are formed. As minimum a jet has only one scattered hadron, for example one pion. Instead of two jets at e+e−-annihilation a quark-antiquark pair can create one neutral vector meson. It must be most symmetrical hadron because a quark-antiquark pair has neutral charges and close flavor, for example ψ/J or other quarkoniums. It is important the most exact masses of the vector mesons are obtained in experiments at e+e−-annihilation. Therefore these vector mesons are the most suitable objects for examination. At e+e—annihilation the next hadron events in the low and mo-derate range of energies are observed: two jets of hadrons or one vector meson. Conserving universality of the jet mechanism, we only shall suppose that there at e+e−-annihilation and especially at energies of quarkoniums can be also generated bound group of quarks or unbroken whole string. It is like a string of pearl or garland or snowflakes. Viewed process essentially differs from observable mono jet[4], the momentum of bound quark group is completely compensated and equal to zero in center-of-mass system of e+e−-pair. This quark group is a real single bound group without other particles. This quark group corresponds to the string model of quark captures from vacuum by first leaders and then by captured quarks etc[5], but in this work we assume the string is not breaking because there goes the full conversion of an initial kinetic energy of leaders into quark-antiquark pairs. After that a bound quark group (unbroken whole string) may be conversed to a resonant particle. Thus, the stage of a whole string was considered as the separate stage of hadronization. Unbroken whole string with total mass of rest equal to experimental mass[6] of meson will be called hereinafter quark flower or briefly flower.The flowers of vector mesons at the e+e−-annihilation must be neutral symmetrical quark groups and the author calculated the flowers with a using first of all neutral groups of one flavor quarks and with colorless configuration (6 or 2 quarks)[7]. In the present paper we shall use the same labels as in[2] with the standard notation for the harmonic quarks (d, u, s, c), and circle-enclosed notation for quarks of complete harmonic oscillators (ⓓ, ⓤ, ⓢ). The calculations of flower configurations are performed exclusively by means of masses of the harmonic quarks and their complete oscillations[1],[8] (see tabl.1). A ratio of mass of any quark to its mass in oscillator is equal to π/2. Also quark masses are bound strongly and simply by definition[3].Table 1. The Masses of Harmonic Quarks
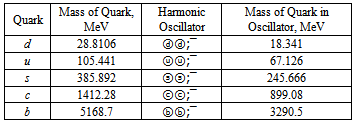 |
| |
|
We begin this searching not on an empty place. In the first time[7] a colorless neutral quark configurations (which can organize temporary or stable shells in hadrons) were studied with using of harmonic quarks. Six-color quark shells of one flavor are the most neutral of all objects of a QCD in the respect of quantum numbers. Investigations in this area have given set of original results[2],[7],[9],[10]. Previous investigations also showed that the number of d-quarks in structure of particles is restricted by one pair or it is not present at all. It is bound by that easiest d-quarks differ on properties from “true” u- and s-quarks[11]. By searching groups of quark flowers we also will use one dd¯pair of quarks. Thus, the base positions for searching were selected following: - Masses of u- and s-quarks in “free” states and harmoniously bound states (ⓤ and ⓢ)[7].- Neutral six-color (colorless) quark shells of one flavor(6s, 6ⓢ, 6u and 6ⓤ) with priority using of more “heavy” neutral groups.- Presence of leading quarks with large probability.
2. Quark Flowers of Vector Mesons
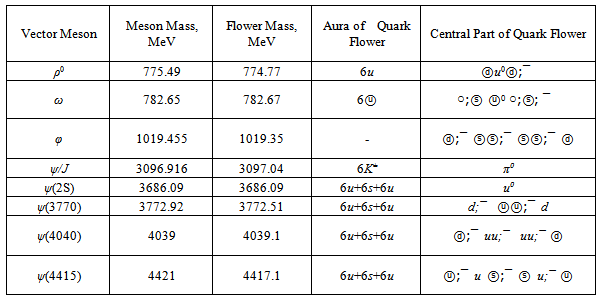
In the given section a results of floral research will be stated for following vector mesons of e+e−-annihilation: ρ(770), ω, φ, ψ/J, ψ(2S), ψ(3770), ψ(4040) and ψ(4415).
2.1. ρ(770) (Mρ=775.49 ±0.34 MeV)
The meson ρ(770) is difficult object for research. It has too greater width of decay and therefore its mass Mρ is defined with a considerable uncertainty. However value Mρ in e+e−-annihilation remained stable a long time and now equal to 775.49 MeV[6]. If ρ(770) has ρ-flower then only one of two six-quark shells is possible: 6u or 6ⓤ with rest masses 632.65 and 402.75 MeV accordingly. In the first case the residual energy 142.84 MeV (Mρ - M6u ) should concentrate on the leaders of single jet. This value was considered in[1],[12] and there it correspond to a quark configuration 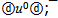 with energy 142.12 MeV. In the second case the residual energy (372.73 MeV) can be represented by neutral quark group:
with energy 142.12 MeV. In the second case the residual energy (372.73 MeV) can be represented by neutral quark group: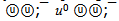 Masses of flowers are 774.77 and 776.70 MeV accordingly, but deviation of first flower mass from experience mass is less. Preliminary flower configuration of ρ(770) is next:
Masses of flowers are 774.77 and 776.70 MeV accordingly, but deviation of first flower mass from experience mass is less. Preliminary flower configuration of ρ(770) is next: 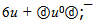 The image of flower is shown on figure 1.
The image of flower is shown on figure 1. | Figure 1. The conditional images of quark flowers ρ and ω |
2.2. ω(782) (Mω=782.65 ±0.12 MeV)
As in case ρ only one of two six-quark shells is possible in flower of ω: 6u or 6ⓤ. The difference energy between ω-mass and first shell is 150.00 MeV and second shell is 379.90 MeV. Hence, to find the ω-flower it is enough to present one of difference energies in the form of quark groups. First value can not be represented in masses of d and u quarks with necessary accuracy. On the contrary the energy 379.90 is easily interpreted by exact group 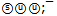 with a rest mass 379.92 MeV. Then the quark flower of ω with mass 782.67 MeV has the next configuration:
with a rest mass 379.92 MeV. Then the quark flower of ω with mass 782.67 MeV has the next configuration: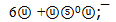 At this shape the ω-flower has only one harmoniously bound strange quark, but in other configuration with the same energy[2] the flower will look balanced fully
At this shape the ω-flower has only one harmoniously bound strange quark, but in other configuration with the same energy[2] the flower will look balanced fully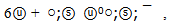 where
where 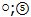 and
and 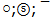 - quark and antiquark of s-oscillator of second rank which is formed of already bound quarks ⓢ and
- quark and antiquark of s-oscillator of second rank which is formed of already bound quarks ⓢ and 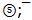 . Quark groups
. Quark groups 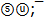 and
and 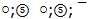 have the same energy 312.79 MeV in harmonic quark model. A ratio of energies of two s-oscillators
have the same energy 312.79 MeV in harmonic quark model. A ratio of energies of two s-oscillators 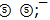 and
and 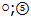
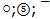 is equal to π/2 also as for quark pair
is equal to π/2 also as for quark pair 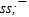 and
and 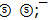 . Obviously the ω-flower has the close strangeness (see figure 1). Probable leaders of the ω-flower are twice harmoniously bound s-quarks (harmonic strong coupling of second level).
. Obviously the ω-flower has the close strangeness (see figure 1). Probable leaders of the ω-flower are twice harmoniously bound s-quarks (harmonic strong coupling of second level).
2.3. φ(1020) (Mφ=1019.455 ±0.02 MeV)
The flower configuration of φ is discovered earlier[2] and given in table 2. It can be presented in the form of one quark chain: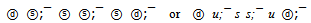
2.4. ψ/J(1S) (Mψ/J =3096.916 ±0.011 MeV)
The ψ/J flower can contain only one “heavy” six-color shells 6s and one shell 6u. The difference between ψ/J mass and these shells is 148.923 MeV. It permits only two groups of leading quarks: 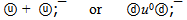 In the first case the residual energy will be equal 14.67 and in second - 6.80 MeV. Thus, if not excess of energy, the meson ψ/J could be interpreted by one of beautiful symmetrical groups:
In the first case the residual energy will be equal 14.67 and in second - 6.80 MeV. Thus, if not excess of energy, the meson ψ/J could be interpreted by one of beautiful symmetrical groups: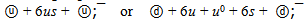 However we have last and single hope to salvage a beautiful quark flower. The quark structure of hypothetical flower has six us-groups. The rest mass of one group has energy 491.332 MeV, and we can replace it with real meson K± with the same quarks
However we have last and single hope to salvage a beautiful quark flower. The quark structure of hypothetical flower has six us-groups. The rest mass of one group has energy 491.332 MeV, and we can replace it with real meson K± with the same quarks 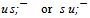 . Remaining sequential, we substitute in flower the leader group
. Remaining sequential, we substitute in flower the leader group  on real meson π0 with same quarks.As a result we obtain a unique beautiful flower of ψ/J: π0 + 6K±Energy of flower (3097.04 ± 0.10 MeV) is in consent with ψ/J mass. Obvious leaders of the ψ/J flower are harmoniously bound a pionic pair of quarks ⓤ +
on real meson π0 with same quarks.As a result we obtain a unique beautiful flower of ψ/J: π0 + 6K±Energy of flower (3097.04 ± 0.10 MeV) is in consent with ψ/J mass. Obvious leaders of the ψ/J flower are harmoniously bound a pionic pair of quarks ⓤ +  . The image of flower is shown on figure 2.
. The image of flower is shown on figure 2.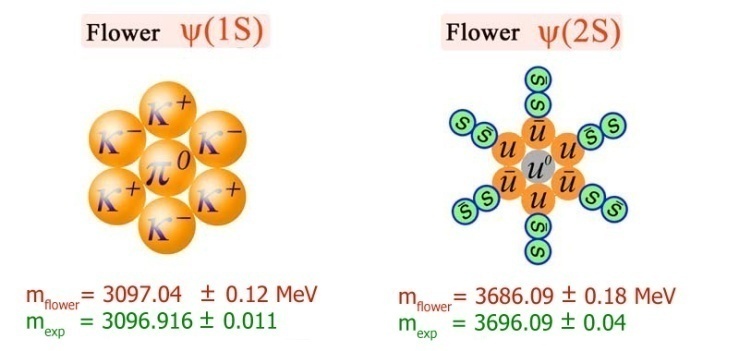 | Figure 2. The conditional images of quark flowers ψ/J and ψ(2S) |
2.5. ψ(2S) (Mψ(2S)= 3686.09 ±0.04 MeV)
The ψ(2S) flower is found also with use of a principle of consecutive filling mass by most heavy shell. The mass of ψ(2S) in the minimum variant can contain only three full color shells:6u + 6s + 6uResidual energy for leaders will be equal: 3686.093 - 12*105.441 - 6*385.892 = 105.448 MeV.Exact hit from the first attempt! It differs from mass of u quark only in the sixth decimal sign and we discovered the beautiful flower of ψ(2S) with only quark configuration (see figure 2) and mass equal to 3686.09 ± 0.18 MeV:u0 + 6u + 6s + 6uThe neutral u0 quark already figured in work[2]. Here we can view it as 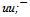 -pair with strictly half annihilation. In other words, the leaders are half quarks u/2 and
-pair with strictly half annihilation. In other words, the leaders are half quarks u/2 and 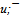 /2.
/2.
2.6. ψ(3770) (Mψ(3770)= 3772.92 ±0.35 MeV)
If shells of ψ(3770) flower are the same as on ψ(2S) flower then residual energy of leaders must be equal to 192.28 MeV. This energy is easily interpreted by neutral symmetrical group of quarks with rest mass 191.87 MeV: 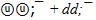 Hence, flower of ψ(3770) probably consists from following shells and quarks:
Hence, flower of ψ(3770) probably consists from following shells and quarks: 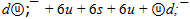
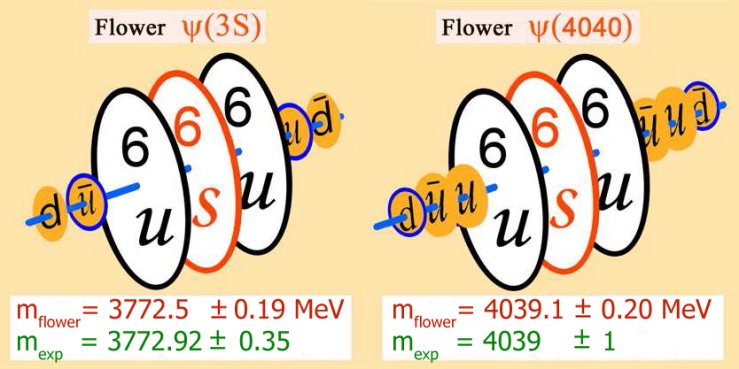 | Figure 3. The conditional images of quark flowers ψ(3S) and ψ(4040) |
The mass of ψ(3770) flower is 3772.51 ± 0.19 MeV and it well agrees with PDG fit[6]. The image of flower is shown on figure 3.
2.7. ψ(4040) (Mψ(4040)=4039 ±1 MeV)
If the ψ(4040) flower has the same shells as ψ(2S) and ψ(3770) flowers then energy of the lead quark group is 458.3 MeV. Configuration of this quark group is simple enough: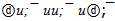 It is similar to the φ-flower at replacement s-quarks on u. Thus, the ψ(4040) flower with mass 4039.1 ±0.20 MeV can be written down so:
It is similar to the φ-flower at replacement s-quarks on u. Thus, the ψ(4040) flower with mass 4039.1 ±0.20 MeV can be written down so: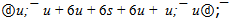 The image of the given variant of the ψ(4040) flower is shown on figure 3.But the situation with a true flower of the ψ (4040) is not defined. The mass of quarkonium ψ(4040) is above a threshold of formation of
The image of the given variant of the ψ(4040) flower is shown on figure 3.But the situation with a true flower of the ψ (4040) is not defined. The mass of quarkonium ψ(4040) is above a threshold of formation of 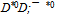 pairs. Hence, besides structures with light quarks there can be a flower structure with
pairs. Hence, besides structures with light quarks there can be a flower structure with 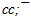 -pair. Only one combination of quarks was found for initial conditions of searching in range 4039 ±1 MeV:
-pair. Only one combination of quarks was found for initial conditions of searching in range 4039 ±1 MeV: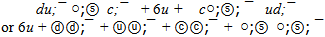 The mass of second flower ψ(4040) is 4038.5 ±0.20 MeV.
The mass of second flower ψ(4040) is 4038.5 ±0.20 MeV.
2.8. ψ(4415) (Mψ(4415)=4421 ±4 MeV)
A search of flower structure of a quarkonium ψ(4415) gives us many variants, two of which are given below: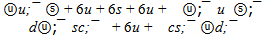 These flowers are similar to flowers ψ(4040). The rest masses of flowers are 4417.1 and 4420.9 MeV. It is difficult to prefer any one flower structure at the experimental uncertainty of quarkonium mass ± 4 MeV.
These flowers are similar to flowers ψ(4040). The rest masses of flowers are 4417.1 and 4420.9 MeV. It is difficult to prefer any one flower structure at the experimental uncertainty of quarkonium mass ± 4 MeV.
2.9. Auras and Center Parts of Quark Flowers
We should select in structures of quark flowers the central parts and flower auras. The flower auras in mesons of ρ, ω, ψ/J, ψ(2S), ψ(3770) (perhaps also ψ(4040) and ψ(4415)) are quite obvious. It is six-color homogeneous (one flavor) shells accordingly: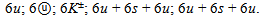 The flower auras of these mesons possess electrical neutrality and full color symmetry. The central quark groups of flowers should be also neutral and symmetrical. The floral results for vector mesons of e+e−-annihilation are summed in the table 2.
The flower auras of these mesons possess electrical neutrality and full color symmetry. The central quark groups of flowers should be also neutral and symmetrical. The floral results for vector mesons of e+e−-annihilation are summed in the table 2.Table 2. The Quark-Floral Structures of Some Vector Mesons and Calculated Flower Masses
 |
| |
|
3. Preliminary Discussion of Results
The discussion of unusual results we begin with a place of flower structures in the scheme of e+e−-annihilation. A detection of quark flowers with masses equal to masses of the vector mesons radically changes the scheme of meson formation. At creation of flower the leading quarks will capture sequentially other quarks till its momentums will be decreased till zero. It is a transformation of full momentum of leaders into other quarks of flower with zero final momentum of each quark. Actually we deal with condensation of quarks on quark leaders. Also formation of quark shells on the leaders can be considered as original high-energy bremsstrahlung. A flower in e+e−-annihilation must be completely colorless and electrically neutral. It can be only six-quark shells or a one-flavor quark-antiquark pairs. Moreover, in case of a ψ/J flower there goes a condensation of kaons on pionic ⓤ-quarks with further transformation of this energy into two heavy  -quarks and its environment. Also similar processes of transformation should take place at creation of ψ(2S) and ψ(3770), as well as probably for ω(783), ψ(4040), ψ(4415). The simple scheme of formation of the vector mesons in the e+e−-annihilation now has more stages: e+e− → virtual photon → leading quarks → quark flower → quark transformation → vector meson.We can to doubt in quantity and content of stages. For example, we can change a stage of photon decay onto the leading quarks by decay onto an aura or whole flower. But, however, exact fit of flower and observational masses already practically does not allow doubt in necessity of change of prior scheme. It is also important to remember the fits were obtained only with first or second try in logical order of floral formation.
-quarks and its environment. Also similar processes of transformation should take place at creation of ψ(2S) and ψ(3770), as well as probably for ω(783), ψ(4040), ψ(4415). The simple scheme of formation of the vector mesons in the e+e−-annihilation now has more stages: e+e− → virtual photon → leading quarks → quark flower → quark transformation → vector meson.We can to doubt in quantity and content of stages. For example, we can change a stage of photon decay onto the leading quarks by decay onto an aura or whole flower. But, however, exact fit of flower and observational masses already practically does not allow doubt in necessity of change of prior scheme. It is also important to remember the fits were obtained only with first or second try in logical order of floral formation.
3.1. ρ(770)
It is the first vector resonance with large width of decay. The beginning of ρ-peak is approximately equal to aura of a ρ-flower (633 MeV). The quark structure of flower and the quantum numbers of triplet do not guess of a condensation of energy into a strange pair of quarks. Probably, after of a flower phase there goes at once a collapse of aura and formation of two pions from central quarks. It explains a small lifetime of ρ(770).
3.2. ω(782)
The width of ω-peak is equal to ~8 MeV[6]. The beginning of peak is ~774 MeV that above a threshold of formation of  -pair only on ~2 MeV. The structure of a ω-flower has a twice coupled strange pair of quarks and it is possible to guess, that after of flower phase a condensation of energy can occur into a pair of the strange quarks in the vector variant. It explains an origin of the singlet state and significant lifetime of ω. Perhaps also just the stage of con- densation leads to anomalous peak increase of cross - section.
-pair only on ~2 MeV. The structure of a ω-flower has a twice coupled strange pair of quarks and it is possible to guess, that after of flower phase a condensation of energy can occur into a pair of the strange quarks in the vector variant. It explains an origin of the singlet state and significant lifetime of ω. Perhaps also just the stage of con- densation leads to anomalous peak increase of cross - section.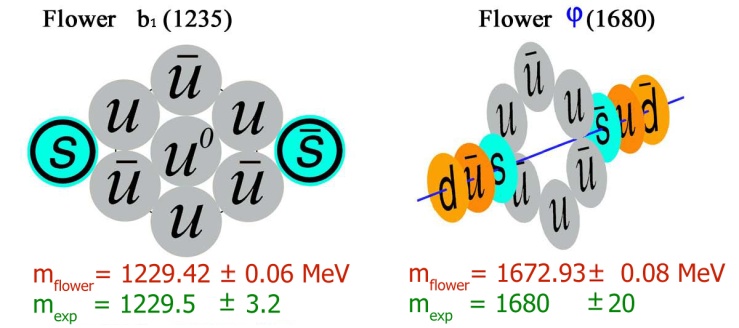 | Figure 4. The conditional images of quark flowers b1(1235) and φ(1680) |
The ω-flower (see figure 1) is unique so much that all quarks of the flower are in bound state, and s-quarks belong even to oscillator of the second level. It enables us to transform the quark flower ω on one level above, preserving physical sense of quark components. The new quark flower with rest mass 1229.4 MeV will by a present for us: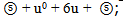 It is a precise mass (1229.5 ±3.2 MeV) of the meson resonance b1(1235), which decays in main mode on ω. The image of b1(1235)-flower is shown on figure 4.
It is a precise mass (1229.5 ±3.2 MeV) of the meson resonance b1(1235), which decays in main mode on ω. The image of b1(1235)-flower is shown on figure 4.
3.3. φ(1020)
Possibly φ-flower is a quark chain (flower without aura) and its quark structure can be written down in two symmetrical variants with the same energy in harmonic quark model: 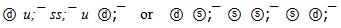 Not clearly, what are the leaders of chain? A presence of
Not clearly, what are the leaders of chain? A presence of 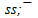 quarks in a flower provides a closed strangeness of φ meson then a quark condensation is not required. However the annihilation of
quarks in a flower provides a closed strangeness of φ meson then a quark condensation is not required. However the annihilation of 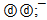 -pair with redistribution of energy in the momentum of quarks and color fields is possible. So far question about the real quark structure of φ remains open.Besides of φ there is one more vector φ(1680) in PDG data[6]. It has been observed in e+e−-annihilation and has the mass 1680 ±20 MeV. Uncertainty in mass of resonance is large and so flower solutions are also many, but supposed flower configuration with mass 1673 MeV is next:
-pair with redistribution of energy in the momentum of quarks and color fields is possible. So far question about the real quark structure of φ remains open.Besides of φ there is one more vector φ(1680) in PDG data[6]. It has been observed in e+e−-annihilation and has the mass 1680 ±20 MeV. Uncertainty in mass of resonance is large and so flower solutions are also many, but supposed flower configuration with mass 1673 MeV is next: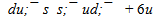 The φ(1680)-flower (see figure 4) has a neutral shell 6u, but in other part it is quite similar to the φ(1019)-flower. The second variant of φ(1019)-flower contains bounded quarks only and permits a transformation of level to mode:
The φ(1680)-flower (see figure 4) has a neutral shell 6u, but in other part it is quite similar to the φ(1019)-flower. The second variant of φ(1019)-flower contains bounded quarks only and permits a transformation of level to mode: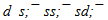 The mass of group is 1601 MeV. Singlet h1(1595 ±15) with the same quantum number as triplet b1(1235) is near.
The mass of group is 1601 MeV. Singlet h1(1595 ±15) with the same quantum number as triplet b1(1235) is near.
3.4. ψ/J(1S)
Uncertainty of ψ/J mass is less in 9 times than for a flower. If flower concept is exact the mass K± can be calculated more exactly with using the masses of ψ/J and π0: MK± = 493.656 ±0.002 MeV. The calculated value agrees with experimental data (493.677 ±0.016 MeV)[6].The kaon condensation on pion requires a careful analysis. A formation of two heavy quarks due to condensation of kaons on u-oscillator of pion arouses the certain doubt. The matter is that though the mass of charged kaon consists almost of masses u- and s-quarks, nevertheless, there are 2.34 (MeV) which relates to kinetic and coupling energies of quarks. As shown in[11] the velocity of u-quark in a kaon achieves 0.2 from velocity of the light. It is difficult to present, how condensation can be executed at high velocities of quarks? Certainly, the relative velocity of u- and s-quarks can be ~0 at some moments. Nevertheless, this problem was leading to idea about the possible flower solution for kaon pairs K+K-. Searching has led to following result: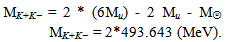 | (1) |
Importance of the equation (1) is obvious. The mass of kaon pair can be also an effect of condensation of two 6u shells except the annihilating group 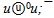 . The scheme of K+K- creation by condensation of u-quarks is given on figure 5. The ψ/J flower and also equation (1) open the way for an operations with kaon condensate. Actually under kaon condensation there can be the hidden u-quark condensation. The calculated value of K±-mass (493.643) is also in a fine consent with experimental data[6], but betters with value 493.642 MeV no DENISOV[13].
. The scheme of K+K- creation by condensation of u-quarks is given on figure 5. The ψ/J flower and also equation (1) open the way for an operations with kaon condensate. Actually under kaon condensation there can be the hidden u-quark condensation. The calculated value of K±-mass (493.643) is also in a fine consent with experimental data[6], but betters with value 493.642 MeV no DENISOV[13].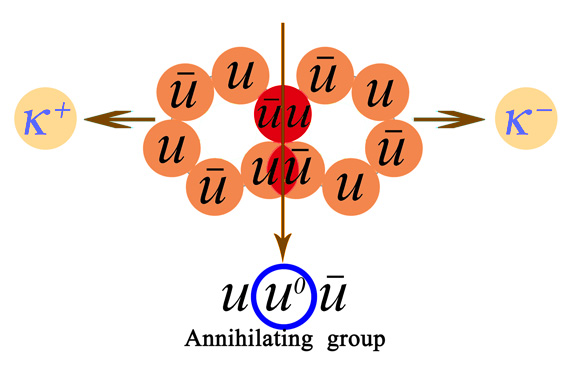 | Figure 5. The flower scheme of K+K- creation |
3.5. ψ(2S)
The ψ(2S) is formed of cleanly quark flower (see fig. 2). It differs from other flowers by the minimal central part u0. Neutral centers on the basis of a u-quark are observed also in flowers of ρ and ω. About u0 we spoke earlier in[2]. The neutral u0 can be represented as u/2 + 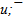 /2, i.e. by u
/2, i.e. by u 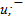 - pair with 50% annihilation. The u0 can be considered also as two virtual leading quarks u
- pair with 50% annihilation. The u0 can be considered also as two virtual leading quarks u 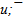 . However it is more probably the center and aura is forming together. After that all and almost all quarks of aura condense onto the u/2 +
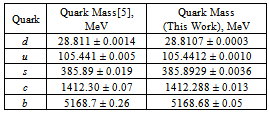
. However it is more probably the center and aura is forming together. After that all and almost all quarks of aura condense onto the u/2 + 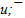 /2.The precision of ψ(2S) mass is 0.04 (~0.001%) and it is 5 times better, than error for flower mass. The masses of harmonic quarks are recalculated with using mass of ψ(2S) and are given in the table 3.
/2.The precision of ψ(2S) mass is 0.04 (~0.001%) and it is 5 times better, than error for flower mass. The masses of harmonic quarks are recalculated with using mass of ψ(2S) and are given in the table 3.Table 3. The Masses of Harmonic Quark
 |
| |
|
Though values of quark masses have remained the same, but the mass errors of quarks considerably decrease if the floral concept is perfectly correct.
3.6. ψ(3770), ψ(4040) and ψ(4415)
The flowers of ψ(3770), ψ(4040) and ψ(4415) have the aura of ψ(2S), but clearly expressed axial quarks. At the same time it needs to note flower configurations for quarkoniums ψ(4040) and ψ(4415) are not final solutions. With this purpose the second flower configurations (containing c-quarks) are given in spite of the fact that charm are suppressed in jets[14]. Nevertheless values R with growth of energy e+e−-annihilation reach the predicted level and, hence, c-quarks are anyway forming. For this reason variants of unbroken jets or flowers with c-quarks are viewed also. We already know, that c-quarks form full-color (colorless) six quark mesons, even in the ground state, for example D0[10]. Therefore formation of 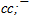 -pair in jet is possible to expect only above a threshold
-pair in jet is possible to expect only above a threshold 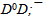 . With growth of energy e+e−-annihilation in an environment of c-quarks will appear and s-quarks, the number of different combinations in an environment of
. With growth of energy e+e−-annihilation in an environment of c-quarks will appear and s-quarks, the number of different combinations in an environment of 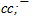 -pairs will increase. Maximal probability of formation
-pairs will increase. Maximal probability of formation 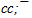 -pairs in jets it is possible to expect at energies of e+e−-pairs more 5 GeV.
-pairs in jets it is possible to expect at energies of e+e−-pairs more 5 GeV.
4. Conclusions
The new meson production mechanism is suggested. It is based on assumption that e+e−-annihilation can form one quark jet in unbroken state. The group of harmonic quarks with zero interquark momentum and a rest mass equal to a meson mass is named as the quark flower. The search of quark flowers in e+e−-annihilation at energies up to 4.5 GeV was performed. The quark flowers are found for next vector mesons: ρ, ω, φ, ψ/J, ψ(2S), ψ(3770), ψ(4040) and ψ(4415). The mesons have symmetrical quark flowers with energy precisely corresponding to their experimental masses. If a quark flowers are real objects then we have a real new mechanism of quark formation, i.e. a strange and charm quarks can be generated by a condensation of more light harmonic quarks. The quark condensation is contrary process to the quark fragmentation. Author assumes the processes of quark condensation can be cause of anomalous high peaks on curve of a cross-section in e+e−-annihilation.Obviously, the investigations with using of the new tool (harmonic quarks) have led us to the active intrusion in a complex field of a hadronization, a field which is practically closed for exact studies. This field is not accessible to modern methods because these methods have not of other such exact instruments as harmonic quarks.
References
| [1] | Teplov O.A., 2006, The exact quantization of the CLEO and BELLE data for D mass differences by the harmonic quarks and oscillators, arXiv: hep-ph/0604247. |
| [2] | Teplov O.A., 2005, Precise mass spectrum of mesons with open charm in the harmonic quarks and oscillators, arXiv: hep-ph/0505267. |
| [3] | Teplov O.A., 2003, Harmonic quarks and their precise masses, arXiv: hep-ph/0306215. |
| [4] | Feldman G.J. et al., 1985, Search for monojet production in e+e−-annihilation, Phys. Rev. Lett., 54(21), 2289-2291. |
| [5] | Andersson B., Gustafson G., Ingelman G. and Sjostrand T.,1983, Parton fragmentation and string dynamics, Phys. Rep.,97(2-3), 31-145. |
| [6] | Nakamura K. et al., 2010, Review of Particle Physics (Particle Data Group), J. Phys. G: Nucl. Part. Phys. 37, 075021. |
| [7] | Teplov O.A., 2004, Harmonic quarks and hadrons up to 1000 MeV, arXiv: hep-ph/0408205. |
| [8] | Teplov O. A., 2009, Quark flowers and quark condensation, arXiv: hep-ph /0906.1687. |
| [9] | Teplov O.A., 2008, The exact interpretation of mass differences in upper part of the charmonium spectrum, arXiv: hep-ph/0807.0068. |
| [10] | Teplov O. A., 2007, The six-quark structure of long-lived D mesons and ψ/J, arXiv: hep-ph/0702008. |
| [11] | Teplov O. A., 2003, Harmonic quarks: properties and some applications, arXiv: hep-ph/0308207. |
| [12] | Bortoletto D. et al. (CLEO Collaboration), 1992, Isospin mass splitting from precision measurements of D-D mass differences, Phys. Rev. Lett., 69(14), 2041-2045. |
| [13] | Eidelman S. et al. (Particle Data Group), 2004, Review of particle physics, Phys. Lett. B, 592, 1. |
| [14] | Scomparin E. (for the NA60 Collab.), 2007, J/ψ production in In-In and p-A collisions, J. Phys. G, 34, 463-469. |

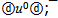 with energy 142.12 MeV. In the second case the residual energy (372.73 MeV) can be represented by neutral quark group:
with energy 142.12 MeV. In the second case the residual energy (372.73 MeV) can be represented by neutral quark group: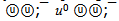 Masses of flowers are 774.77 and 776.70 MeV accordingly, but deviation of first flower mass from experience mass is less. Preliminary flower configuration of ρ(770) is next:
Masses of flowers are 774.77 and 776.70 MeV accordingly, but deviation of first flower mass from experience mass is less. Preliminary flower configuration of ρ(770) is next: 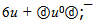 The image of flower is shown on figure 1.
The image of flower is shown on figure 1.
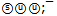 with a rest mass 379.92 MeV. Then the quark flower of ω with mass 782.67 MeV has the next configuration:
with a rest mass 379.92 MeV. Then the quark flower of ω with mass 782.67 MeV has the next configuration: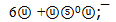 At this shape the ω-flower has only one harmoniously bound strange quark, but in other configuration with the same energy[2] the flower will look balanced fully
At this shape the ω-flower has only one harmoniously bound strange quark, but in other configuration with the same energy[2] the flower will look balanced fully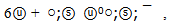 where
where 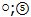 and
and 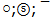 - quark and antiquark of s-oscillator of second rank which is formed of already bound quarks ⓢ and
- quark and antiquark of s-oscillator of second rank which is formed of already bound quarks ⓢ and 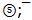 . Quark groups
. Quark groups 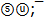 and
and 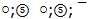 have the same energy 312.79 MeV in harmonic quark model. A ratio of energies of two s-oscillators
have the same energy 312.79 MeV in harmonic quark model. A ratio of energies of two s-oscillators 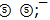 and
and 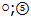
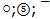 is equal to π/2 also as for quark pair
is equal to π/2 also as for quark pair 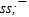 and
and 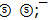 . Obviously the ω-flower has the close strangeness (see figure 1). Probable leaders of the ω-flower are twice harmoniously bound s-quarks (harmonic strong coupling of second level).
. Obviously the ω-flower has the close strangeness (see figure 1). Probable leaders of the ω-flower are twice harmoniously bound s-quarks (harmonic strong coupling of second level).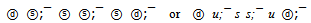
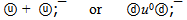 In the first case the residual energy will be equal 14.67 and in second - 6.80 MeV. Thus, if not excess of energy, the meson ψ/J could be interpreted by one of beautiful symmetrical groups:
In the first case the residual energy will be equal 14.67 and in second - 6.80 MeV. Thus, if not excess of energy, the meson ψ/J could be interpreted by one of beautiful symmetrical groups: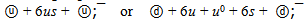 However we have last and single hope to salvage a beautiful quark flower. The quark structure of hypothetical flower has six us-groups. The rest mass of one group has energy 491.332 MeV, and we can replace it with real meson K± with the same quarks
However we have last and single hope to salvage a beautiful quark flower. The quark structure of hypothetical flower has six us-groups. The rest mass of one group has energy 491.332 MeV, and we can replace it with real meson K± with the same quarks 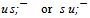 . Remaining sequential, we substitute in flower the leader group
. Remaining sequential, we substitute in flower the leader group 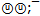 on real meson π0 with same quarks.As a result we obtain a unique beautiful flower of ψ/J: π0 + 6K±Energy of flower (3097.04 ± 0.10 MeV) is in consent with ψ/J mass. Obvious leaders of the ψ/J flower are harmoniously bound a pionic pair of quarks ⓤ +
on real meson π0 with same quarks.As a result we obtain a unique beautiful flower of ψ/J: π0 + 6K±Energy of flower (3097.04 ± 0.10 MeV) is in consent with ψ/J mass. Obvious leaders of the ψ/J flower are harmoniously bound a pionic pair of quarks ⓤ +  . The image of flower is shown on figure 2.
. The image of flower is shown on figure 2.
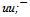 -pair with strictly half annihilation. In other words, the leaders are half quarks u/2 and
-pair with strictly half annihilation. In other words, the leaders are half quarks u/2 and 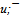 /2.
/2.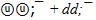 Hence, flower of ψ(3770) probably consists from following shells and quarks:
Hence, flower of ψ(3770) probably consists from following shells and quarks: 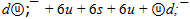

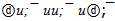 It is similar to the φ-flower at replacement s-quarks on u. Thus, the ψ(4040) flower with mass 4039.1 ±0.20 MeV can be written down so:
It is similar to the φ-flower at replacement s-quarks on u. Thus, the ψ(4040) flower with mass 4039.1 ±0.20 MeV can be written down so: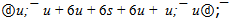 The image of the given variant of the ψ(4040) flower is shown on figure 3.But the situation with a true flower of the ψ (4040) is not defined. The mass of quarkonium ψ(4040) is above a threshold of formation of
The image of the given variant of the ψ(4040) flower is shown on figure 3.But the situation with a true flower of the ψ (4040) is not defined. The mass of quarkonium ψ(4040) is above a threshold of formation of 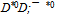 pairs. Hence, besides structures with light quarks there can be a flower structure with
pairs. Hence, besides structures with light quarks there can be a flower structure with 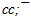 -pair. Only one combination of quarks was found for initial conditions of searching in range 4039 ±1 MeV:
-pair. Only one combination of quarks was found for initial conditions of searching in range 4039 ±1 MeV: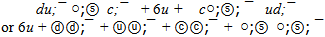 The mass of second flower ψ(4040) is 4038.5 ±0.20 MeV.
The mass of second flower ψ(4040) is 4038.5 ±0.20 MeV.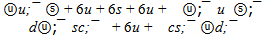 These flowers are similar to flowers ψ(4040). The rest masses of flowers are 4417.1 and 4420.9 MeV. It is difficult to prefer any one flower structure at the experimental uncertainty of quarkonium mass ± 4 MeV.
These flowers are similar to flowers ψ(4040). The rest masses of flowers are 4417.1 and 4420.9 MeV. It is difficult to prefer any one flower structure at the experimental uncertainty of quarkonium mass ± 4 MeV.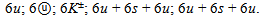 The flower auras of these mesons possess electrical neutrality and full color symmetry. The central quark groups of flowers should be also neutral and symmetrical. The floral results for vector mesons of e+e−-annihilation are summed in the table 2.
The flower auras of these mesons possess electrical neutrality and full color symmetry. The central quark groups of flowers should be also neutral and symmetrical. The floral results for vector mesons of e+e−-annihilation are summed in the table 2. -quarks and its environment. Also similar processes of transformation should take place at creation of ψ(2S) and ψ(3770), as well as probably for ω(783), ψ(4040), ψ(4415). The simple scheme of formation of the vector mesons in the e+e−-annihilation now has more stages: e+e− → virtual photon → leading quarks → quark flower → quark transformation → vector meson.We can to doubt in quantity and content of stages. For example, we can change a stage of photon decay onto the leading quarks by decay onto an aura or whole flower. But, however, exact fit of flower and observational masses already practically does not allow doubt in necessity of change of prior scheme. It is also important to remember the fits were obtained only with first or second try in logical order of floral formation.
-quarks and its environment. Also similar processes of transformation should take place at creation of ψ(2S) and ψ(3770), as well as probably for ω(783), ψ(4040), ψ(4415). The simple scheme of formation of the vector mesons in the e+e−-annihilation now has more stages: e+e− → virtual photon → leading quarks → quark flower → quark transformation → vector meson.We can to doubt in quantity and content of stages. For example, we can change a stage of photon decay onto the leading quarks by decay onto an aura or whole flower. But, however, exact fit of flower and observational masses already practically does not allow doubt in necessity of change of prior scheme. It is also important to remember the fits were obtained only with first or second try in logical order of floral formation.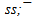 -pair only on ~2 MeV. The structure of a ω-flower has a twice coupled strange pair of quarks and it is possible to guess, that after of flower phase a condensation of energy can occur into a pair of the strange quarks in the vector variant. It explains an origin of the singlet state and significant lifetime of ω. Perhaps also just the stage of con- densation leads to anomalous peak increase of cross - section.
-pair only on ~2 MeV. The structure of a ω-flower has a twice coupled strange pair of quarks and it is possible to guess, that after of flower phase a condensation of energy can occur into a pair of the strange quarks in the vector variant. It explains an origin of the singlet state and significant lifetime of ω. Perhaps also just the stage of con- densation leads to anomalous peak increase of cross - section.
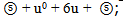 It is a precise mass (1229.5 ±3.2 MeV) of the meson resonance b1(1235), which decays in main mode on ω. The image of b1(1235)-flower is shown on figure 4.
It is a precise mass (1229.5 ±3.2 MeV) of the meson resonance b1(1235), which decays in main mode on ω. The image of b1(1235)-flower is shown on figure 4.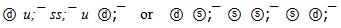 Not clearly, what are the leaders of chain? A presence of
Not clearly, what are the leaders of chain? A presence of  quarks in a flower provides a closed strangeness of φ meson then a quark condensation is not required. However the annihilation of
quarks in a flower provides a closed strangeness of φ meson then a quark condensation is not required. However the annihilation of 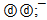 -pair with redistribution of energy in the momentum of quarks and color fields is possible. So far question about the real quark structure of φ remains open.Besides of φ there is one more vector φ(1680) in PDG data[6]. It has been observed in e+e−-annihilation and has the mass 1680 ±20 MeV. Uncertainty in mass of resonance is large and so flower solutions are also many, but supposed flower configuration with mass 1673 MeV is next:
-pair with redistribution of energy in the momentum of quarks and color fields is possible. So far question about the real quark structure of φ remains open.Besides of φ there is one more vector φ(1680) in PDG data[6]. It has been observed in e+e−-annihilation and has the mass 1680 ±20 MeV. Uncertainty in mass of resonance is large and so flower solutions are also many, but supposed flower configuration with mass 1673 MeV is next: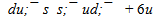 The φ(1680)-flower (see figure 4) has a neutral shell 6u, but in other part it is quite similar to the φ(1019)-flower. The second variant of φ(1019)-flower contains bounded quarks only and permits a transformation of level to mode:
The φ(1680)-flower (see figure 4) has a neutral shell 6u, but in other part it is quite similar to the φ(1019)-flower. The second variant of φ(1019)-flower contains bounded quarks only and permits a transformation of level to mode: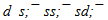 The mass of group is 1601 MeV. Singlet h1(1595 ±15) with the same quantum number as triplet b1(1235) is near.
The mass of group is 1601 MeV. Singlet h1(1595 ±15) with the same quantum number as triplet b1(1235) is near.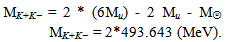
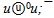 . The scheme of K+K- creation by condensation of u-quarks is given on figure 5. The ψ/J flower and also equation (1) open the way for an operations with kaon condensate. Actually under kaon condensation there can be the hidden u-quark condensation. The calculated value of K±-mass (493.643) is also in a fine consent with experimental data[6], but betters with value 493.642 MeV no DENISOV[13].
. The scheme of K+K- creation by condensation of u-quarks is given on figure 5. The ψ/J flower and also equation (1) open the way for an operations with kaon condensate. Actually under kaon condensation there can be the hidden u-quark condensation. The calculated value of K±-mass (493.643) is also in a fine consent with experimental data[6], but betters with value 493.642 MeV no DENISOV[13].
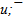 /2, i.e. by u
/2, i.e. by u 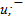 - pair with 50% annihilation. The u0 can be considered also as two virtual leading quarks u
- pair with 50% annihilation. The u0 can be considered also as two virtual leading quarks u 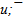 . However it is more probably the center and aura is forming together. After that all and almost all quarks of aura condense onto the u/2 +
. However it is more probably the center and aura is forming together. After that all and almost all quarks of aura condense onto the u/2 + 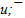 /2.The precision of ψ(2S) mass is 0.04 (~0.001%) and it is 5 times better, than error for flower mass. The masses of harmonic quarks are recalculated with using mass of ψ(2S) and are given in the table 3.
/2.The precision of ψ(2S) mass is 0.04 (~0.001%) and it is 5 times better, than error for flower mass. The masses of harmonic quarks are recalculated with using mass of ψ(2S) and are given in the table 3.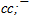 -pair in jet is possible to expect only above a threshold
-pair in jet is possible to expect only above a threshold 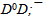 . With growth of energy e+e−-annihilation in an environment of c-quarks will appear and s-quarks, the number of different combinations in an environment of
. With growth of energy e+e−-annihilation in an environment of c-quarks will appear and s-quarks, the number of different combinations in an environment of 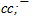 -pairs will increase. Maximal probability of formation
-pairs will increase. Maximal probability of formation  -pairs in jets it is possible to expect at energies of e+e−-pairs more 5 GeV.
-pairs in jets it is possible to expect at energies of e+e−-pairs more 5 GeV. Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML

