H. M. M. Mansour, Nady Bakhet
Department of Physics, Cairo University, Cairo, 12613, Egypt
Correspondence to: H. M. M. Mansour, Department of Physics, Cairo University, Cairo, 12613, Egypt.
| Email: |  |
Copyright © 2012 Scientific & Academic Publishing. All Rights Reserved.
Abstract
In the present work we search for Resonance in the dielectron events produced in proton-proton collisions at LHC using Monte Carlo simulation programs which may be Z'_{B-L} heavy neutral boson. To detect this resonance at LHC we used the data which are produced from pp collision of Pythia8 produced events at different energies for LHC then we use the angular distribution for the dielectron produced from Z'_{B-L} decay channels to detect the Z'_{B-L}signal. B-L extension of the SM model predicts the existence of a Z'_{B-L}heavy neutral massive boson at high energies and from our results which we had simulated for Z'_{B-L}in the B-L extension of standard model we predict that a Z'_{B-L}boson will be found at LHC and has a mass in the range from 1 TeV to 1.5 TeV.
Keywords:
Gauge Bosons, LHC, Monte Carlo Simulation, Z Prime Particles, Cross Sections, Branching Ratios, Extended
Cite this paper:
H. M. M. Mansour, Nady Bakhet, "Search for Resonance in the Dilepton Mass at LHC Using MC Simulation", Journal of Nuclear and Particle Physics, Vol. 2 No. 6, 2012, pp. 153-156. doi: 10.5923/j.jnpp.20120206.04.
1. Introduction
The fact that neutrinos are massive indicates that the Standard Model (SM) requires extension. B-L model is an extension for the SM which is based on the gauge group GB-L=SU (3)C x SU(2)L x U(1)Y x U(1)B-L. The invariance of the Lagrangian under this gauge symmetry implies the existence of a new gauge boson (beyond the SM ones) and the spontaneous symmetry breaking in this model provides a natural explanation for the presence of three right-handed neutrinos in addition to an extra gauge boson and a new scalar Higgs. Therefore, one can observe a very interesting phenomenology which is different from the SM results and it can be tested at the LHC(see e.g. Ref.[1]). An extra neutral massive gauge boson corresponding to B−L gauge symmetry is predicted. There are many models which contain extra gauge bosons. These models can be classified into two categories depending on whether or not they arise in a GUT scenario. In some of these models, the Z′ and the SM Z do not have true mass due to mixing. This mixing induces the couplings between the extra Z′ boson and the SM fermions .In our model of B−L extension of the SM, the extra Z′_{B-L} boson and the SM fermions are coupled through the non-vanishing B−L quantum numbers. Searching for Z′_{B-L} is accessible via a clean dilepton signal at LHC. We will simulate B − L extension of the SM, Which is based on the gauge group SU(3)C × SU(2)L× U(1)y × U(1)B-L using MC programs at LHC and search for Z'_{B-L} bosons in dielectron events produced in pp collisions at different energies of LHC using the Monte Carlo event generator PYTHIA8 as in[2- 5] and the software tools (Data analysis ROOT package and ROOFIT package to fit any resulted histogram to get P.D.F. (Probability density function)).Also we use MadGraph5 / Madevent and CALCHEP programs. To identify the Z'_{B-L} à e+ e− signal, we use the dielectron angular distribution[6]. The leptonic decays Z'_{B-L} àℓ+ℓ− provide the most distinctive signature for observing the Z'_{B-L} signal at a Large Hadrons Collider. We will study the production of Z'_{B-L} at LHC and the different branching ratios. Also we will study Z'_{B-L} using dielectron angular distribution and analyse the results by using simulation event generator PYTHIA8 and other software tools, ROOT and ROOFIT.
2. Results
In this section we present our results for simulation of Z'_{B-L} in the B − L model using MC simulation. We first present production cross-sections of Z'_{B-L} at the LHC as a function of Z'_{B-L} mass for various g'' values (where g'' is the U (1)B-L gauge coupling constant) and for various energies for LHC, branching ratios as a function of Z'_{B-L} mass for heavy neutrino mass hV= 200 GeV which will have an effect on the different results of Z'_{B-L} due to its heavy mass. We obtained different results in comparison with those reported as in[7] where the analysis in this paper did not take into account the new heavy neutrino which is an important signature of the B-L model as in[8-10] .Also they did not give any branching ratio for heavy neutrino. After that we give the result of Z'_{B-L} total width as a function of Z'_{B-L} mass for various values of g′'.
2.1. Production Cross Section
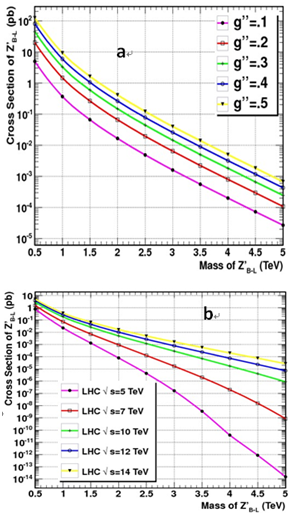 | Figure 1. Cross-sections for Z'_{B-L} as a function of Z'B-L masses (a) For various g'' values and fixed value of LHC CM energy 14 TeV (b) For various LHC CM energies and fixed value of g''=0.2 |
In figure 1 we present the production cross sections for Z'_{B-L} for the most relevant production mechanisms. We can compare the production cross sections for different CM energies. Figure 1(a) gives the cross sections in the B − L model for Z'_{B-L} at the LHC as a function of Z'_{B-L} mass for various g'' values (where g'' is the U (1)B-L gauge coupling constant) and energy of LHC = 14 TeV . Figure 2 (b) gives cross sections in the B − L model for Z'_{B-L} at the LHC for energies √s = 5, 7, 10, 12 and 14 TeV at fixed value of g''=0.2.At the patron level, the Z'_{B-L} production cross section depends on two main parameters the mass of Z'_{B-L} and the coupling constant g''. Therefore, the model B-L is controlled by two parameters: first, the mass of the Z'_{B-L} second, the coupling constant g" determining Z'_{B-L} couplings. There are two experimental constraints on these two parameters. The first comes from direct search for heavy neutral gauge bosons at the Fermi Lab, which excludes a Z'_{B-L} mass less than 600 GeV. The second limit comes from LEP where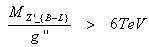 | (1) |
The extra neutral gauge boson Z'_{B-L} acquires a mass due to the B −L gauge symmetry breaking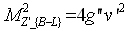 | (2) |
where g'' is the U(1)B-L gauge coupling constant and v' is the symmetry breaking scale| Table 1. B-L quantum number for different particles |
| | Particle | l | eR | vR | q | | YB-L | -1 | -1 | -1 | 1/3 |
|
|
The production cross sections for the Z'_{B-L} signal in figure 1 are computed using MadGraph5 and PYTHIA8 where we generated the process pp --> Z'_{B-L} of B-L model using Mad- Graph5 and export this process to PHYTHIA8 then the main switches will stay on for Initial state Radiation(ISR) , Final State Radiation(FSR), FSR Resonances, and Decay. Hadronization allows resonance decays and master switches for multiparton interactions stay on. PartonLevel: ISR= On, PartonLevel: FSR=On, PartonLevel: FSR in Process= On, PartonLevel: FSR in Resonances=On, Process Level: all = On, Process Level: resonance Decays=On, Parton Level: all=On, PartonLevel: Remnants=On, Parton Level: MPI=On, HadronLevel: all=On, Hadron Level: Hadronize=On, HadronLevel: Decay= On, Hadron Level: Bose Einstein=On
2.2. Branching Ratios
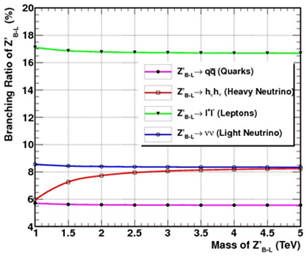 | Figure 2. Branching ratios for Z'B-L boson as a function of Z'_{B-L } mass for heavy neutrino mass hv= 200 GeV |
From fig. 2, the branching ratios of for Z_{B-L} different quarks are equal approximately and the branching ratios for different leptons are higher than those for the quarks and also the branching ratios for heavy neutrino (which have a mass 200 GeV). In particular, BR (Z'_{B-L} → ℓ+ℓ−) varies between 17% and 17.5% where (ℓ = electron, muon, tau). But for heavy neutrino BR(Z'_{B-L} → hv hv) and for light neutrino BR(Z'_{B-L} → ν ν) they vary between 8.5% and 9%. BR (Z'_{B-L} → qq) varies between 5.5% and 6%. Z'_{B-L} can decay into one light and one heavy neutrino such a channel is highly suppressed by the corresponding (heavy-light) neutrino mixing and thus it can safely be neglected. Heavy neutrino is the most characteristic for B-L model so it affects other branching ratios because it has a massive neutrino in comparison with the SM neutrino. From figure 2 we can search for Z'_{B-L} at LHC via a clean dilepton signal which can be one of the first new physics signatures to be observed at the LHC. We will study Z'_{B-L} in this paper by using the channel decay of Z'_{B-L} to electrons pair using PYTHIA8 and turn off all other channels of decay of the Z'_{B-L} particle where the ratio of dielctron channel is the highest one and then use these commands.pythia.readString("900032:onMode=0"),pythia.readString("900032:m0=1000")pythia.readString ("900032:onIfAll=11 -11") where the first command turn off all decay channels of Z'_{B-L} and the second one set the mass of Z'_{B-L} to 1000GeV and the third command permits the decay of Z'_{B-L} to electron and positron only.
2.3. Total Width of Z'_{B-L}
The Z'_{B-L} boson decays only to fermions at tree-level and its width is given by the following expression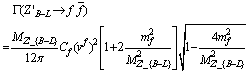 | (3) |
where mf is the mass and Cf the number of colours of the fermions type f .In Figs. 3 and 4 we present the total decay width of the Z'_{B-L} as a function of Z'_{B-L} and g'', respectively where the other parameters were held fixed to three different values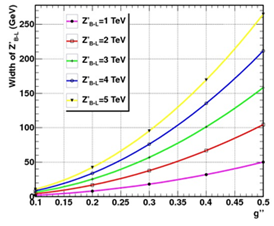 | Figure 3. Total width for Z'_{B-L} boson as a function of g'' for different values of Z'_{B-L} mass |
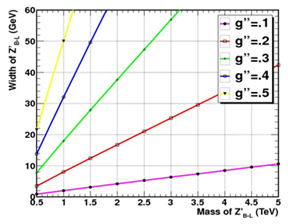 | Figure 4. Total width for Z'_{B-L} boson as a function of mass Z'_{B-L} for fixed values of g'' |
From figures 3 and 4 we see that the total width of a Z'_{B-L} gauge boson varies from a few to hundreds of GeV over a mass range of 1 TeV < Z'_{B-L} < 5 TeV, depending on the value of g''. The decay widths of Z'_{B-L} → ffbar in this model are then given by: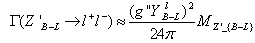 | (4) |
Figures 3 and 4 are calculated by PYTHIA8 using the commands: pythia. event[i]. m Width(), Parton Level: ISR=On, Parton Level: FSR=On.
2.4. Dielectron Angular Distribution
By using dielectron angular distribution cos (θ*) where θ* is the angle in the dielectron rest reference frame between the negative electron and the incident incoming quark. PTHIA8 gives θ only in Lab frame but we use θ* here which is in the rest frame so we must convert from lab frame to rest frame to get θ* by using boost vector.We define two additional reference frames:(a) The colliding proton CM frame denoted by O (this frame is identical to the laboratory frame) and (b) The rest frame of the dilepton system denoted by O*. The dilepton system is boosted along the beam axis. The z-axis is chosen as the direction of one of the beams, and it is then identical for O and O* frames. It should be noted that there is a sign ambiguity in the measurement of cos (θ*), since for a particular event, there is no information about whether the incoming quark comes from the positive or negative z directions. Instead, it is useful to consider the quantity cos (θ*ß), where θ*ß is the angle between the dilepton system boost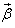 (relative to the O frame) and the lepton direction as in [11]
(relative to the O frame) and the lepton direction as in [11]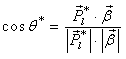 | (5) |
Where the boost vector is 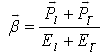 | (6) |
In order to obtain 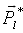 the boost vector of the dilepton system should be found and the transformation to the O* frame should be performed
the boost vector of the dilepton system should be found and the transformation to the O* frame should be performed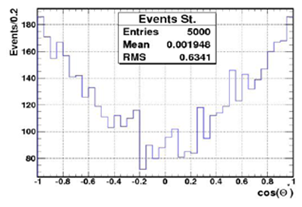 | Figure 5. Angular distribution of dielectron of Z'_{B-L} boson decay where forward electrons cos (θ*)>0 and backward electrons cos (θ*) < 0 |
3. Conclusions
In this work we have presented the LHC potential to discover a heavy neutral massive gauge boson Z'_{B-L} of the B-L extension of the SM model using MC programs where we have simulated the production cross section at different center of mass energies of LHC for various values of the coupling constant g'' and branching ratios of Z_{B-L} to all different decay channels to fermions. We presented the total width of Z'_{B-L} as a function of Z'_{B-L} mass. Also we presented the decay of Z'_{B-L} into an electron–positron pair and we have presented dielectron angular distribution. All these signatures predict the existence of a new gauge boson Z'_{B-L} at LHC.
ACKNOWLEDGEMENTS
It is a pleasure to thank T. Sjostrand, for useful discussions of PYTHIA, L. Basso and C. Duhr for useful discussions of B-L model and J. Alwall for useful discussions of MadGraph5/ MadEvent.
References
| [1] | S. Khalil, S. Moretti, “Heavy neutrinos, Z’ and Higgs bosons at the LHC: new particles from an old symmetry” arXiv:1207.1590 [hep-ph] Jul 2012. |
| [2] | T. Sjostrand, S. Mrenna, and P. Skands, J. High Energy Phys. 05 (2006) 026. |
| [3] | k T. Sjostrand, CERN-LCGAPP-2005-05 July 2005k |
| [4] | T.Sjostrand,http://home.thep.lu.se/~torbjorn/php8160 |
| [5] | L. Basso, (PhD Thesis, university of Southampton) ArXiv: 1106.4462v1 [hep-ph] 22 Jun 2011 |
| [6] | L. Basso, (Master Thesis,Universit`a degli Studi di Padova,2007). |
| [7] | W. Emam, P Min´e 2008 J. Phys. G: Nucl. Part. Phys. 35 115008. |
| [8] | CDF Collaboration- arXiv:hep-ex/0602045v1 24 Feb 2006. |
| [9] | L. Basso, arXiv:0903.4777[hep-ph] 16 Sep 2009 |
| [10] | T.Sjostrand T, Eden P, Friberg C, Lonnblad L, Miu G, Mrenna S and Norrbin Comput. Phys. |
| [11] | T. Sjostrand et al., Comput. Phys. 135, 238 (2001). |

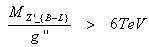
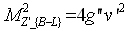

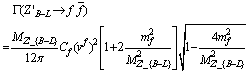


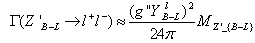
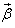 (relative to the O frame) and the lepton direction as in [11]
(relative to the O frame) and the lepton direction as in [11]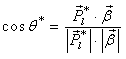
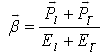
 the boost vector of the dilepton system should be found and the transformation to the O* frame should be performed
the boost vector of the dilepton system should be found and the transformation to the O* frame should be performed
 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-Text HTML
Full-Text HTML