-
Paper Information
- Next Paper
- Paper Submission
-
Journal Information
- About This Journal
- Editorial Board
- Current Issue
- Archive
- Author Guidelines
- Contact Us
Journal of Nuclear and Particle Physics
p-ISSN: 2167-6895 e-ISSN: 2167-6909
2012; 2(6): 132-141
doi: 10.5923/j.jnpp.20120206.01
Molar Electron Mass and the Basics of TOE
U. V. S. Seshavatharam1, S. Lakshminarayana2
1Honorary faculty, I-SERVE, Alakapuri, Hyderabad-35, AP, India
2Dept. of Nuclear Physics, Andhra University, Visakhapatnam-03, AP, India
Correspondence to: U. V. S. Seshavatharam, Honorary faculty, I-SERVE, Alakapuri, Hyderabad-35, AP, India.
| Email: |  |
Copyright © 2012 Scientific & Academic Publishing. All Rights Reserved.
The subject of unification is very interesting and very complicated. Implementing the gravitational constant in atomic and nuclear physics is a challenging task. Still string theory and super gravity are not in a position to bring down the Planck scale to the nuclear scale. In this connection, considering the ‘molar electron mass’ an attempt is made to study the four fundamental interactions in a unified manner.
Keywords: Gravity, Avogadro Number, Integral Charge Quark SUSY, Quark Fermion, Quark Boson, Quark Baryon, Quark Meson, Higgs Fermion, Higgs Boson, Strong Coupling Constant, SEMF Energy Coefficients, Electron and the Nucleon’S Magnetic Moments, Gram Mole
Cite this paper: U. V. S. Seshavatharam, S. Lakshminarayana, "Molar Electron Mass and the Basics of TOE", Journal of Nuclear and Particle Physics, Vol. 2 No. 6, 2012, pp. 132-141. doi: 10.5923/j.jnpp.20120206.01.
Article Outline
1. Introduction
- String theory and Super gravity are in the race of developing the real TOE. It is very interesting to implement the gravitational constant in atomic and nuclear physics. With gravity - interpreting the known atomic and nuclear phenomena, fitting and estimating the elementary particle rest masses and their coupling strengths is a very hard and sensitive job. Einstein spent most of his life in unifying gravity and electromagnetism. But by that time, strong interaction was in its budding stage. Still string theory and super gravity are not in a position to bring down the Planck scale to the nuclear scale. In this critical situation, by considering the “molar electron mass”, an attempt is made to understand the secrets of unification. On 21 December 2011 a new meson of rest energy
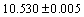 GeV was detected in CERN - LHC and the ATLAS detector. This new meson, known as
GeV was detected in CERN - LHC and the ATLAS detector. This new meson, known as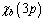 , consists of two parts - an elementary particle known as a ‘beauty’ quark and its opposite antiquark, which are bound together by a ‘strong force’[1]. Its existence was predicted in our published paper[2] : page-278, table-16, last row, last column. Before going further, authors request the interested readers to please go through the two published papers[2] and[3]. This paper is a combined and unified version of the published papers[2,3] and proceedings of the DAE symposium on nuclear physics 2011, India[4,5]. Please note that in our previous paper[2] it was suggested that: boson is the super symmetric boson of the top quark fermion and the charged Higgs boson pair generates the neutralized boson. It was also suggested that[3,5] Higgs charged boson and W boson couples together to form a neutral boson of rest energy 126 GeV. Its existence was detected and is under open discussion[6,7]. Another interesting idea is: W boson pair generates a neutral boson of rest energy 161 GeV. This is our prediction and needs to be verified.
, consists of two parts - an elementary particle known as a ‘beauty’ quark and its opposite antiquark, which are bound together by a ‘strong force’[1]. Its existence was predicted in our published paper[2] : page-278, table-16, last row, last column. Before going further, authors request the interested readers to please go through the two published papers[2] and[3]. This paper is a combined and unified version of the published papers[2,3] and proceedings of the DAE symposium on nuclear physics 2011, India[4,5]. Please note that in our previous paper[2] it was suggested that: boson is the super symmetric boson of the top quark fermion and the charged Higgs boson pair generates the neutralized boson. It was also suggested that[3,5] Higgs charged boson and W boson couples together to form a neutral boson of rest energy 126 GeV. Its existence was detected and is under open discussion[6,7]. Another interesting idea is: W boson pair generates a neutral boson of rest energy 161 GeV. This is our prediction and needs to be verified.2. Key Assumptions in Unification
- The subject of unification is very interesting and very complicated. By implementing the Avogadro number N as a scaling factor in unification program, one can probe the constructional secrets of elementary particles. The Planck’s quantum theory of light, thermodynamics of stars, black holes and cosmology totally depends upon the famous Boltzmann constant
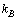 which in turn depends on the Avogadro number[8]. Thus it can be suggested that, Avogadro number is more fundamental and characteristic than the Boltzmann constant and indirectly plays a crucial role in the formulation of the quantum theory of radiation. In this connection it is noticed that, ‘molar electron mass’ plays a very interesting role in nuclear and particle physics. With the following four assumptions- the string theory[9-11], super gravity[12,13] and strong gravity[14-22] can be studied in a unified manner. Assumption-1: Nucleon behaves as if it constitutes molar electron mass. (Or) Molar electron mass
which in turn depends on the Avogadro number[8]. Thus it can be suggested that, Avogadro number is more fundamental and characteristic than the Boltzmann constant and indirectly plays a crucial role in the formulation of the quantum theory of radiation. In this connection it is noticed that, ‘molar electron mass’ plays a very interesting role in nuclear and particle physics. With the following four assumptions- the string theory[9-11], super gravity[12,13] and strong gravity[14-22] can be studied in a unified manner. Assumption-1: Nucleon behaves as if it constitutes molar electron mass. (Or) Molar electron mass 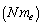 plays a crucial role in nuclear and particle physics.Assumption-2: The key conceptual link that connects the gravitational and non-gravitational forces is - the classical force limit
plays a crucial role in nuclear and particle physics.Assumption-2: The key conceptual link that connects the gravitational and non-gravitational forces is - the classical force limit 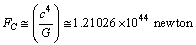 | (1) |
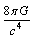 It has multiple applications in Black hole physics and Planck scale physics[23]. It has to be measured either from the experiments or from the cosmic and astronomical observations. Assumption-3: Ratio of ‘classical force limit (
It has multiple applications in Black hole physics and Planck scale physics[23]. It has to be measured either from the experiments or from the cosmic and astronomical observations. Assumption-3: Ratio of ‘classical force limit (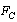 )’ and ‘weak force magnitude
)’ and ‘weak force magnitude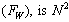 where N is a large number close to the Avogadro number.
where N is a large number close to the Avogadro number. 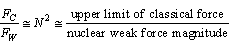 | (2) |
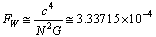 newton and can be considered as the characteristic nuclear weak string tension. It can be measured in the particle accelerators.Assumption-4: In modified quark SUSY, if
newton and can be considered as the characteristic nuclear weak string tension. It can be measured in the particle accelerators.Assumption-4: In modified quark SUSY, if 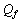 is the mass of quark fermion and
is the mass of quark fermion and 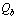 is the mass of quark boson, then
is the mass of quark boson, then 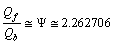 | (3) |
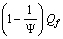 represents the effective fermion mass. The number
represents the effective fermion mass. The number 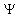 can be fitted with the following empirical relation
can be fitted with the following empirical relation 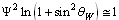 .
.3. Basic Ideas in ‘Modified’ Quark Super Symmetry
- Till today there is no reason for the question: why there exists 6 individual quarks? Till today no experiment reported a free fractional charge quark. Authors humble opinion is nuclear charge (either positive or negative) constitutes 6 different flavours and each flavour holds certain mass. Charged flavour can be called as a quark. It is neither a fermion nor a boson. A fermion is a container for different charges, a charge is a container for different flavours and each flavour is a container for certain matter. If charged matter rests in a fermionic container it is a fermion and if charged matter rests in a bosonic container it is a boson. The fundamental questions to be answered are : what is a charge? why and how opposite charges attracts each other? why and how there exists a fermion? and why and how there exists a boson? Here interesting thing is that if 6 flavours are existing with 6 different masses then a single charge can have one or two or more flavours simultaneously. Since charge is a common property, mass of the multiple flavour charge seems to be the geometric mean of the mass of each flavour. If charge with flavour is called as a quark then charge with multi flavours can be called as a hybrid quark. Hybrid quark generates a multi flavour baryon. It is a property of the strong interaction space - time - charge. This is just like different tastes or different smells of matter. Important consequence of this idea is that- for generating a baryon there is no need to couple 3 fractional charge quarks.1. There exists nature friendly integral charge quark fermions. 2. For every integral charge quark fermion there exists a corresponding integral charge quark boson. Quark fermion and quark boson mass ratio is close to 2.2627. 3. There exists integral charged massive quark fermi-gluons and integral charged massive quark boso-gluons. (Fermi-gluon means massive gluons having fermion behaviour and boso-gluon means massive gluons having boson behaviour. Quark femi-gluon can be called as the ‘quark baryon’ and quark boso-gluon can be called as ‘quark meson’). 4. Quark fermi-gluon or quark baryon masses can be expressed as
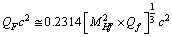 and Quark boso-gluon or quark meson masses can be expressed as
and Quark boso-gluon or quark meson masses can be expressed as 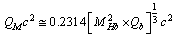 where
where  are the rest masses of quark fermion and quark boson respectively and
are the rest masses of quark fermion and quark boson respectively and  are the Higgs charged fermion and Higgs charged boson respectively. 5.
are the Higgs charged fermion and Higgs charged boson respectively. 5. 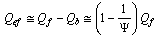 acts as the effective quark fermion. Effective quark baryon mass can be expressed as
acts as the effective quark fermion. Effective quark baryon mass can be expressed as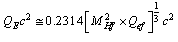 . These effective quark baryons play a vital role in fitting the unstable baryon masses. Quark meson masses play a vital role in fitting the unstable meson masses.6. Characteristic nuclear fermion is
. These effective quark baryons play a vital role in fitting the unstable baryon masses. Quark meson masses play a vital role in fitting the unstable meson masses.6. Characteristic nuclear fermion is 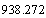 MeV and its corresponding nuclear boson is
MeV and its corresponding nuclear boson is 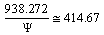 MeV. This boson couples with the light quark bosons or light quark mesons and generates neutral ground states. Thus it is the mother of presently believed strange mesons like 493, 548, 1020 MeV and 783, 890 MeV etc. 7. Charged ground state baryon rest energy is
MeV. This boson couples with the light quark bosons or light quark mesons and generates neutral ground states. Thus it is the mother of presently believed strange mesons like 493, 548, 1020 MeV and 783, 890 MeV etc. 7. Charged ground state baryon rest energy is 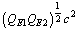 or
or 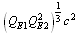 or
or 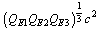 where
where 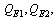 and
and 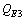 represents any three effective quark baryons. Integral charge light quark bosons’ in one or two numbers couples with the ground or excited effective quark baryons and generates doublets and triplets. This is just like ‘absorption of photons by the electron’.8. Rest energy of nucleon is close to
represents any three effective quark baryons. Integral charge light quark bosons’ in one or two numbers couples with the ground or excited effective quark baryons and generates doublets and triplets. This is just like ‘absorption of photons by the electron’.8. Rest energy of nucleon is close to 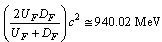 and nucleon rest energy difference is close to
and nucleon rest energy difference is close to 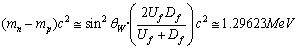 9. Only oppositely charged quark mesons couples together to form a neutral meson. No two quark fermions couples together to form a meson. Neutral ground state meson rest energy is close to
9. Only oppositely charged quark mesons couples together to form a neutral meson. No two quark fermions couples together to form a meson. Neutral ground state meson rest energy is close to 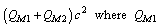 and
and 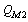 represents any two quark mesons. 10. Fine rotational levels of any ground state energy
represents any two quark mesons. 10. Fine rotational levels of any ground state energy 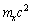 can be expressed as, if n =1,2,3…, and
can be expressed as, if n =1,2,3…, and 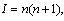
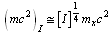 and
and 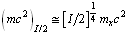 . Super fine rotational levels can be obtained as
. Super fine rotational levels can be obtained as 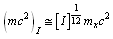 and
and 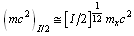 .
. 3.1. The Lepton-quark Mass Generator
- With its earlier defined magnitude[2] and in the recently published paper[3] it was defined that
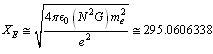 | (4) |
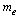 is the rest mass of electron. It can be called as the lepton-quark-nucleon mass generator. It plays a very interesting role in nuclear and particle physics. Using this number leptons, quarks and nucleon rest masses can be fitted[2]. It can be expressed as
is the rest mass of electron. It can be called as the lepton-quark-nucleon mass generator. It plays a very interesting role in nuclear and particle physics. Using this number leptons, quarks and nucleon rest masses can be fitted[2]. It can be expressed as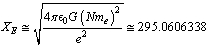 | (5) |
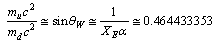 | (6) |
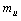 is the rest mass of up quark,
is the rest mass of up quark,  is the rest mass of down quark and
is the rest mass of down quark and 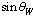 is the weak coupling angle. In the modified SUSY, the fermion and boson mass ratio
is the weak coupling angle. In the modified SUSY, the fermion and boson mass ratio 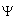 can be fitted in the following way.
can be fitted in the following way.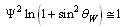 | (7) |
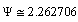 If
If 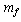 is the mass of fermion and
is the mass of fermion and 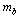 is the mass of its corresponding boson then
is the mass of its corresponding boson then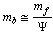 | (8) |
3.2. To fit the Muon and Tau Rest Masses
- Using
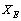 charged muon and tau masses[3,24] were fitted in the following way.
charged muon and tau masses[3,24] were fitted in the following way.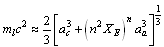 | (9) |
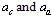 are the coulombic and asymmetric energy coefficients of the semi empirical mass formula and
are the coulombic and asymmetric energy coefficients of the semi empirical mass formula and 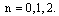 This is an approximate relation. Qualitatively this expression is connected with
This is an approximate relation. Qualitatively this expression is connected with 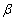 decay. Accuracy can be improved with the following relation.
decay. Accuracy can be improved with the following relation. 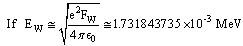 | (10) |
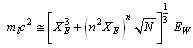 | (11) |
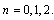 If it is true that weak decay is due to weak nuclear force, then
If it is true that weak decay is due to weak nuclear force, then 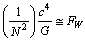 can be considered as the characteristic weak force magnitude. Please refer the published papers for the mystery of electro weak bosons and the Higgs boson[2,3]. Please see table-1.
can be considered as the characteristic weak force magnitude. Please refer the published papers for the mystery of electro weak bosons and the Higgs boson[2,3]. Please see table-1.
|
3.3. To correlate the Electron, Muon, Proton and the Charged Pion Rest Masses
- From the above table-1, if
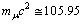 MeV, surprisingly it is noticed that,
MeV, surprisingly it is noticed that,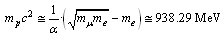 | (12) |
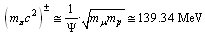 | (13) |
3.4. Nucleons, Up & Down Quarks and the Strong Coupling Constant
- It our earlier published papers[2,3] it was also defined that
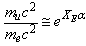 | (14) |
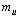 is the up quark rest mass and
is the up quark rest mass and 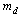 is the down quark rest mass respectively. In our earlier papers, suggested up quark mass is 4.4 MeV and down quark mass is 9.476 MeV. With these magnitudes it is noticed that,
is the down quark rest mass respectively. In our earlier papers, suggested up quark mass is 4.4 MeV and down quark mass is 9.476 MeV. With these magnitudes it is noticed that, 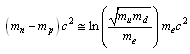 | (15) |
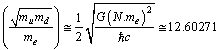 | (16) |
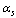 - it is also noticed that[24],
- it is also noticed that[24],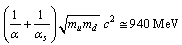 | (17) |
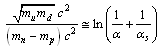 | (18) |
3.5. To Fit the Strong Coupling Constant
- The strong coupling constant
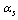 is a fundamental parameter of the Standard Model. It plays a more central role in the QCD analysis of parton densities in the moment space. QCD does not predict the actual value of
is a fundamental parameter of the Standard Model. It plays a more central role in the QCD analysis of parton densities in the moment space. QCD does not predict the actual value of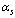 , however it definitely predicts the functional form of energy dependence
, however it definitely predicts the functional form of energy dependence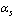 . The value of
. The value of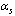 , at given energy or momentum transfer scale, must be obtained from experiment. Determining
, at given energy or momentum transfer scale, must be obtained from experiment. Determining 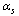 at a specific energy scale is therefore a fundamental measurement, to be compared with measurements of the electromagnetic coupling, of the elementary electric charge, or of the gravitational constant. Considering perturbative QCD calculations from threshold corrections, its recent obtained value at
at a specific energy scale is therefore a fundamental measurement, to be compared with measurements of the electromagnetic coupling, of the elementary electric charge, or of the gravitational constant. Considering perturbative QCD calculations from threshold corrections, its recent obtained value at 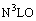 [25] is
[25] is 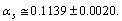 At lower side
At lower side 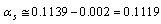 and at higher side
and at higher side 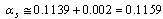 It can be fitted or defined in the following way.
It can be fitted or defined in the following way. 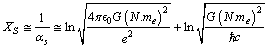 | (19) |
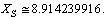
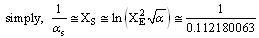 | (20) |
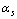 It is true that the proposed definition is conceptually not matching with the current definitions of the strong coupling constant. But the proposed definition considers all the fundamental gravitational and non-gravitational physical constants in a unified manner. This proposal can be given a chance. With this magnitude it is noticed that
It is true that the proposed definition is conceptually not matching with the current definitions of the strong coupling constant. But the proposed definition considers all the fundamental gravitational and non-gravitational physical constants in a unified manner. This proposal can be given a chance. With this magnitude it is noticed that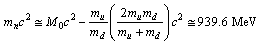 | (21) |
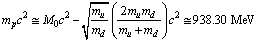 | (22) |
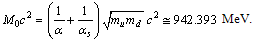
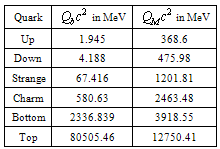
4. Integral Charge Quark Fermions and their SUSY Bosons
- In the previous papers authors suggested that up, strange and bottom quarks are in geometric series. Similarly down, charm and top quarks are in another geometric series. Obtained quark fermion masses can be compared with the current estimates[24]. Up and down fermion masses can be given as
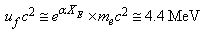 | (23) |
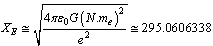 and
and 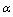 is the fine structure ratio.
is the fine structure ratio.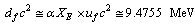 | (24) |
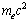 = rest energy of electron,
= rest energy of electron, 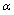 = fine structure ratio ,
= fine structure ratio , 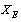 = proposed lepton mass generator. It is very interesting to note that
= proposed lepton mass generator. It is very interesting to note that 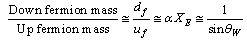 | (25) |
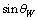 can be related with up and down quark mass ratio. Proposed USB geometric ratio is
can be related with up and down quark mass ratio. Proposed USB geometric ratio is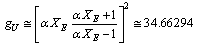 | (26) |
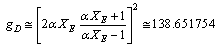 | (27) |
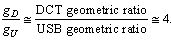 | (28) |
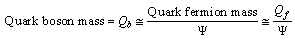 | (29) |
|
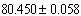 GeV and
GeV and 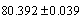 GeV. Please refer M. Yao et al[24] recommended PDG data. Really this is a great coincidence and support for the proposed new idea of ‘‘fermion-boson" unification scheme. This strongly supports super symmetry with small modifications.
GeV. Please refer M. Yao et al[24] recommended PDG data. Really this is a great coincidence and support for the proposed new idea of ‘‘fermion-boson" unification scheme. This strongly supports super symmetry with small modifications. 4.1. Beta decay, Higg’s Charged Fermion and Its Boson
- It is well established that in Beta decay electron is instantaneously created from neutron and this nuclear weak force is mediated by W and Z bosons. If W boson is really the SUSY partner of top quark then the role of W boson in weak decay seems to be nothing. Its role is taken up by the newly proposed Higgs charged boson of rest energy close to 45.6 GeV. Its rest energy is equal to half the rest energy of neutral boson. Semi empirically it is noticed that
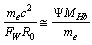 | (30) |
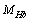 is the rest mass of charged Higgs boson and
is the rest mass of charged Higgs boson and 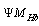 is its fermionic form.
is its fermionic form. 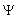 is a unified SUSY fermion and boson mass ratio =2.2627.
is a unified SUSY fermion and boson mass ratio =2.2627. 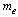 is the rest mass of electron,
is the rest mass of electron, 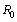 is nuclear characteristic charge radius. Mass of
is nuclear characteristic charge radius. Mass of 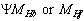 can be expressed as
can be expressed as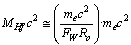 | (31) |
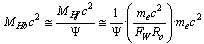 | (32) |
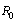 . Based on strong nuclear gravity it was also noticed that
. Based on strong nuclear gravity it was also noticed that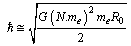 | (33) |
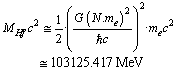 | (34) |
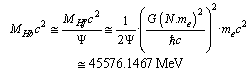 | (35) |
4.2. Rest Energy of the Neutral Z Boson
- From above estimation, neutral Z boson rest energy can be given as
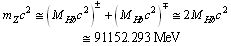 | (36) |
4.3. Recently Discovered Boson of Rest Energy 126 GeV
- Close to the predicted rest energy of Higgs boson, recently a new boson of rest energy 124 to 160 GeV was reported[6,7]. Surprising thing is that its existence is not matching with the current theoretical predictions. In this critical situation, with the help of strong nuclear gravity and modified super symmetry concepts, authors made an attempt to understand the origin of this new boson[3]. In our previous paper[2] it was suggested that: W boson is the super symmetric boson of the top quark fermion and the charged Higgs boson pair generates the neutralized Z boson. It is noticed that Higgs charged boson and top quark boson couples together to form a new neutral boson of rest energy 126.0 GeV. This is a very interesting observation. Like Z boson it can decay into 2 charged particles.
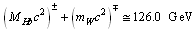 | (37) |
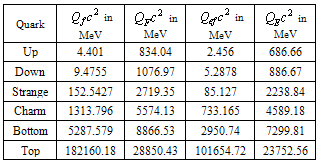
5. Quark Baryon and Quark Meson Masses with SUSY Higgs Charged Particle
- In our earlier published paper it it was assumed that[2], if
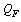 is the quark baryon rest mass
is the quark baryon rest mass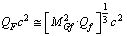 | (38) |
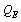 is the quark effective baryon rest mass,
is the quark effective baryon rest mass,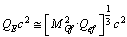 | (39) |
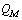 is the quark meson rest mass,
is the quark meson rest mass,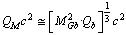 | (40) |
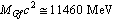 and its bosonic form
and its bosonic form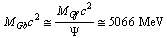 . With reference to the newly proposed Higgs charged fermion and boson[3], above relations can be expressed as
. With reference to the newly proposed Higgs charged fermion and boson[3], above relations can be expressed as 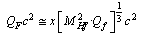 | (41) |
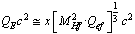 | (42) |
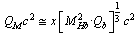 | (43) |
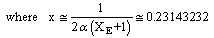 | (44) |
|
|
5.1. Rest energy of the Nucleon
- From table-3 it is noticed that, nucleon mass is very close to the harmonic mean of the up baryon and down baryon masses.
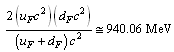 | (45) |
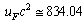 MeV and
MeV and 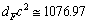 MeV. It is also noticed that,
MeV. It is also noticed that, 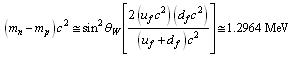 | (46) |
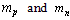 are the rest masses of proton and neutron respectively.
are the rest masses of proton and neutron respectively.5.2. Super Fine Levels of 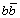 Neutral Mesons
Neutral Mesons
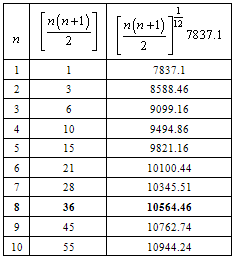
- In this model no 2 baryons couples together to form a neutral meson. Please note that only bottom meson and anti bottom meson couples together to form a neutral meson. The ground state rest energy is equal to 2*3918.55 = 7837.1 MeV. It’s super fine levels can be expressed as
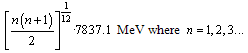 Please see the following table-5. In this table at
Please see the following table-5. In this table at 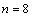 obtained rest energy is 10564.46 MeV and can be compared with the newly discovered
obtained rest energy is 10564.46 MeV and can be compared with the newly discovered 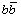 meson. It can be suggested that, average of any two successive levels can also be seen as an excited state. In the similar way excited levels of
meson. It can be suggested that, average of any two successive levels can also be seen as an excited state. In the similar way excited levels of 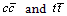 can be understood[2]. Not only that, for the integral charge quark model,
can be understood[2]. Not only that, for the integral charge quark model, 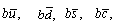 etc excited levels can be predicted. With the same idea
etc excited levels can be predicted. With the same idea 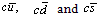 excited levels can also be predicted and fitted[2].
excited levels can also be predicted and fitted[2].
|
5.3. To Fit the Size of Proton
- It is noticed that,
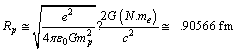 | (47) |
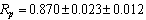 fm. This type of coincidence can not be ignored in the unification scheme.
fm. This type of coincidence can not be ignored in the unification scheme.5.4. Scattering Distance between Electron and the Nucleus
- If
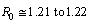 fm is the minimum scattering distance between electron and the nucleus, it is noticed that,
fm is the minimum scattering distance between electron and the nucleus, it is noticed that, 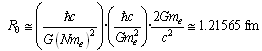 | (48) |
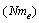 is the molar electron mass. Here also it is very interesting to consider the role of the Schwarzschild radius of the ‘electron mass’ . Thus the two macroscopic physical constants N and G can be expressed in the following way.
is the molar electron mass. Here also it is very interesting to consider the role of the Schwarzschild radius of the ‘electron mass’ . Thus the two macroscopic physical constants N and G can be expressed in the following way.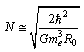 | (49) |
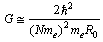 | (50) |
5.5 Electromagnetic and Gravitational Force Ratio of the Proton, Proton-electron Mass Ratio and the Squared Avogadro Number
- Semi empirically it is noticed that
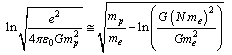 | (51) |
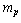 is the proton rest mass and
is the proton rest mass and 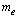 is the electron rest mass. Thus
is the electron rest mass. Thus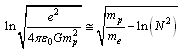 | (52) |
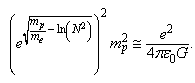 | (53) |
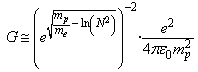 | (54) |
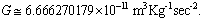 Avogadro number can be expressed as
Avogadro number can be expressed as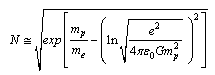 | (55) |
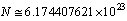
6. To Fit the Semi Empirical Mass Formula Energy Coefficients
- The semi-empirical mass formula (SEMF) is used to approximate the mass and various other properties of an atomic nucleus[28,29]. As the name suggests, it is based partly on theory and partly on empirical measurements. The theory is based on the liquid drop model proposed by George Gamow and was first formulated in 1935 by German physicist Carl Friedrich von Weizsacker. Based on the ‘least squares fit’, volume energy coefficient is
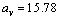 MeV, surface energy coefficient is
MeV, surface energy coefficient is 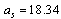 MeV, coulombic energy coefficient is
MeV, coulombic energy coefficient is 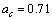 MeV, asymmetric energy coefficient is
MeV, asymmetric energy coefficient is 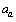 = 23.21 MeV and pairing energy coefficient is
= 23.21 MeV and pairing energy coefficient is 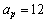 MeV. The semi empirical mass formula is
MeV. The semi empirical mass formula is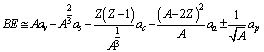 | (56) |
6.1. The Coulombic Energy Coefficient
- It can be defined as,
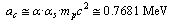 | (57) |
6.2. The Surface and Volume Energy Coefficients
- Surface energy coefficient can be defined as
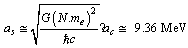 | (58) |
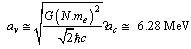 | (59) |
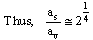 | (60) |
6.3. The Asymmetry and Pairing Energy Coefficients
- Asymmetry energy coefficient can be defined as
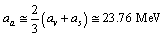 | (61) |
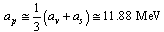 | (62) |
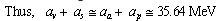 | (63) |
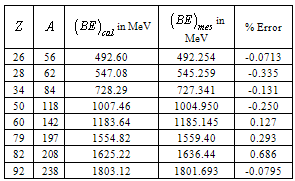
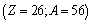 to
to  nuclear binding energy is calculated and compared with the measured binding energy[30]. Column-3 represents the calculated binding energy and column-4 represents the measured binding energy. If this procedure is found to be true and valid then with a suitable fitting procedure qualitatively and quantitatively magnitudes of the proposed SEMF binding energy coefficients can be refined.
nuclear binding energy is calculated and compared with the measured binding energy[30]. Column-3 represents the calculated binding energy and column-4 represents the measured binding energy. If this procedure is found to be true and valid then with a suitable fitting procedure qualitatively and quantitatively magnitudes of the proposed SEMF binding energy coefficients can be refined.
|
6.4. Proton-nucleon Stability
- It is noticed that
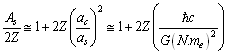 | (64) |
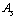 is the stable mass number of Z This is a direct relation. Assuming the proton number Z in general, for all atoms, lower stability can be fitted directly with the following relation[28].
is the stable mass number of Z This is a direct relation. Assuming the proton number Z in general, for all atoms, lower stability can be fitted directly with the following relation[28].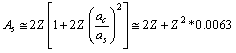 | (65) |
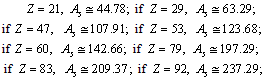 Stable super heavy elements can be predicted with this relation. In between
Stable super heavy elements can be predicted with this relation. In between  obtained
obtained 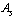 is lower compared to the actual
is lower compared to the actual 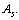 It is noticed that, upper stability in light and medium atoms up to
It is noticed that, upper stability in light and medium atoms up to 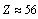 can be fitted with the following relation.
can be fitted with the following relation.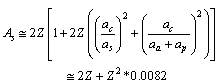 | (66) |
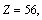 obtained upper
obtained upper 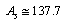 Note that, for
Note that, for 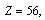 actual stable
actual stable 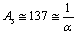 where
where 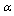 is the fine structure ratio. This seems to be a nice and interesting coincidence. In between 0.0063 and 0.0082, for light and medium atoms up to
is the fine structure ratio. This seems to be a nice and interesting coincidence. In between 0.0063 and 0.0082, for light and medium atoms up to 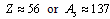 mean stability can be fitted with the following relation.
mean stability can be fitted with the following relation.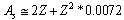 | (67) |
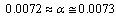 Thus up to
Thus up to 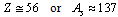 mean stability can be expressed as
mean stability can be expressed as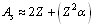 | (68) |
6.5. To fit and Predict the Magic Numbers
- After 1932, experimental data on nuclei repeatedly revealed that in the nucleus, there exists a series of magic numbers, called so, because nuclei with these values for the atomic number Z and/or neutron number N, showed exceptional stability[31,32]. The observed magic numbers are: 2,8,20,28,50,82 and 126. The separation energy for one proton or one neutron is very large for a nucleus with Z or N magic. The probability of nuclei with neutron numbers 20,28,50,82 or 126 capturing a neutron is much less than that of their neighbouring nuclei. Considering
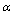 as the characteristic stability number, in a reverse order, magic numbers 82,50,28,20 and 8 can be fitted[33]. Data indicates that for heavy elements stability is achieved when neutron-proton ratio approaches
as the characteristic stability number, in a reverse order, magic numbers 82,50,28,20 and 8 can be fitted[33]. Data indicates that for heavy elements stability is achieved when neutron-proton ratio approaches 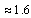 Let us define a new number k in the following way:
Let us define a new number k in the following way: 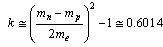 | (69) |
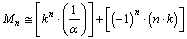 | (70) |
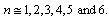 Thus
Thus 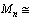 81.81,50.77,28.0,20.33,7.77 and 10.09. After rounding off the values to the nearest even integers, we get, 82,50,28,20,8 and 10. At n=7
81.81,50.77,28.0,20.33,7.77 and 10.09. After rounding off the values to the nearest even integers, we get, 82,50,28,20,8 and 10. At n=7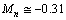 and thus the series seems to be closed at n = 6 itself. Here magic numbers 2 and 126 are missing. The predicted new light magic number is 10. The proposed expression is very simple. It clearly indicates that
and thus the series seems to be closed at n = 6 itself. Here magic numbers 2 and 126 are missing. The predicted new light magic number is 10. The proposed expression is very simple. It clearly indicates that 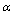 is strongly interconnected with nuclear closed shells.Heavy magic numbers above and below 126 can be predicted with the following expression.
is strongly interconnected with nuclear closed shells.Heavy magic numbers above and below 126 can be predicted with the following expression.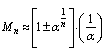 | (71) |
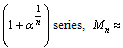 , 138.04,148.74,163.62,177.09,188.26,197.38,For,
, 138.04,148.74,163.62,177.09,188.26,197.38,For, 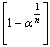 series,
series,  136.04,125.33,110.46,96.98,85.81,76.68,Fine tuning can be achieved if it is assumed that
136.04,125.33,110.46,96.98,85.81,76.68,Fine tuning can be achieved if it is assumed that 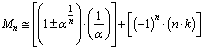 | (72) |
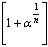 series,
series, 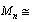 137.43, 149.94, 161.18, 179.49, 185.25, 200.99,For,
137.43, 149.94, 161.18, 179.49, 185.25, 200.99,For, 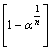 series,
series, 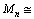 135.43, 126.53, 108.65, 99.39, 82.80, 80.29,After rounding off the values to the nearest even integers, we get,
135.43, 126.53, 108.65, 99.39, 82.80, 80.29,After rounding off the values to the nearest even integers, we get,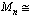 136,150,160,178,184,200, and
136,150,160,178,184,200, and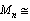 134,126,108,98,82,80,Magic number 184 can be observed in
134,126,108,98,82,80,Magic number 184 can be observed in 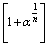 series and 126 can be observed in
series and 126 can be observed in 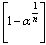 series.
series. 6.6. Nuclear Binding Energy with 2 Terms and Only one Energy Constant
- Nuclear binding energy can be fitted with 2 terms or 4 factors with
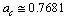 MeV as the single energy constant. First term can be expressed as
MeV as the single energy constant. First term can be expressed as 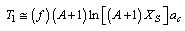 | (73) |
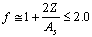 and
and 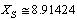 is the strong coupling constant. Second term can be expressed as
is the strong coupling constant. Second term can be expressed as 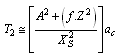 | (74) |
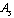 ,
, 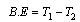 | (75) |
 Above 2 terms can be put into 4 factors as
Above 2 terms can be put into 4 factors as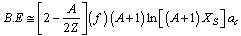 | (76) |
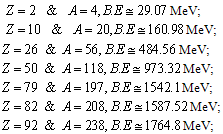 These relations can be considered for further research and analysis positively.
These relations can be considered for further research and analysis positively. 7. Magnetic Moments of the Nucleon
- If
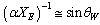 magnetic moment of electron can be expressed as
magnetic moment of electron can be expressed as 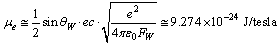 | (77) |
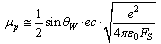 | (78) |
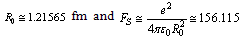 newton is the strong force magnitude. Thus
newton is the strong force magnitude. Thus 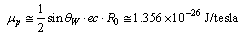 | (79) |
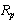 magnetic moment of neutron can be fitted as
magnetic moment of neutron can be fitted as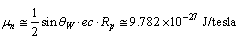 | (80) |
8. Mystery of the Gram Mole
- If
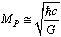 is the Planck mass and
is the Planck mass and 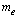 is the rest mass of electron, semi empirically it is observed that,
is the rest mass of electron, semi empirically it is observed that, 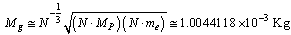 | (81) |
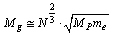 | (82) |
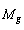 is just crossing the mass of one gram. If
is just crossing the mass of one gram. If 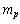 is the rest mass of proton,
is the rest mass of proton,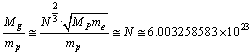 | (83) |
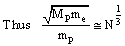 | (84) |
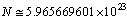 More accurate empirical relation is
More accurate empirical relation is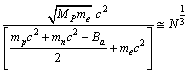 | (85) |
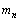 is the rest mass of neutron, and
is the rest mass of neutron, and 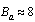 MeV is the mean binding energy of nucleon. Obtained value of
MeV is the mean binding energy of nucleon. Obtained value of 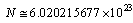
9. Conclusions
- Here it is very important to understand the role of the proposed ‘molar electron mass’. If it represents and indicates the existence of a massive heavy charged particle, automatically Avogadro number can be eliminated. It is having multiple applications in particle physics and cosmology. Authors are working in this new direction. According to Hawking in particular, ‘M-theory is the only candidate for a complete theory of the universe’. Nevertheless physicists, such as Feynman and Glashow, have criticized string theory for not providing novel experimental predictions at accessible energy scales. The success of any TOE depends on – how it couples the Planck scale and the nuclear scale. Please note that, in its initial stage, string theory was originated for understanding the strong interaction. In this connection, by coupling the proposed ideas with the basic concepts of String theory or Super gravity, basic ideas of unification can be refined. Not only that Planck scale and nuclear scale can be interlinked. Further research, analysis and experimental data may reveal the facts.
ACKNOWLEDGEMENTS
- The first author is indebted to professor K. V. Krishna Murthy, Chairman, Institute of Scientific Research on Vedas (I-SERVE), Hyderabad, India and Shri K. V. R. S. Murthy, former scientist IICT (CSIR) Govt. of India, Director, Research and Development, I-SERVE, for their valuable guidance and great support in developing this subject.
 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-Text HTML
Full-Text HTML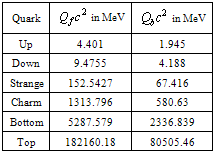
 meson rest energies
meson rest energies